EM@直线的参数方程
文章目录
- abstract
- 直线参数方程
- 从运动轨迹的角度
- 从普通方程转换导参数方程
- 向量法
- 参数方程间的转换
- 从第3型转化为第2型方程组
- 例
abstract
- 平面直线的参数方程的3种表示形式
- 直线参数方程间的转换
直线参数方程
- 以下从不同角度推导直线参数方程
- 分别记为第1,2,3形式参数方程
从运动轨迹的角度
- 直线可以看作是质点匀速运动的曲线
- 设质点从 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0)出发,沿着与 x x x轴成 α \alpha α角的方向作匀速直线运动,其速录为 v 0 v_0 v0,把速度再 x , y x,y x,y轴上分解,大小分别为 v x = v 0 cos α v_x=v_0\cos\alpha vx=v0cosα, v y = v 0 sin α v_y=v_0\sin{\alpha} vy=v0sinα
- 设 M ( x , y ) M(x,y) M(x,y)为 t t t时刻质点所在位置,则如下参数方程组
(1)( t ⩾ 0 ) (t\geqslant{0}) (t⩾0)- x = x 0 + v x t = x 0 + t v 0 cos α x=x_0+v_x{t}=x_0+tv_0\cos\alpha x=x0+vxt=x0+tv0cosα;
- y = y 0 + v y t = y 0 + t v 0 sin α y=y_0+v_y{t}=y_0+tv_0\sin\alpha y=y0+vyt=y0+tv0sinα;
- 若不考虑物理意义,取参数 t ∈ ( − ∞ , + ∞ ) t\in(-\infin,+\infin) t∈(−∞,+∞),方程组(1)就是直线的一种参数方程,参数为 t t t
从普通方程转换导参数方程
- 设直线的点斜式方程为 y − y 0 = k ( x − x 0 ) y-y_0=k(x-x_0) y−y0=k(x−x0)
- 其中 k = tan α k=\tan{\alpha} k=tanα, α \alpha α为直线的倾斜角( α ∈ [ 0 , π ) \alpha\in[0,\pi) α∈[0,π));
- 则 y − y 0 = tan α ( x − x 0 ) y-y_0=\tan{\alpha}(x-x_0) y−y0=tanα(x−x0)= sin α cos α ( x − x 0 ) \frac{\sin{\alpha}}{\cos\alpha}(x-x_0) cosαsinα(x−x0), ( α ≠ π 2 ) (\alpha\neq{\frac{\pi}{2}}) (α=2π)
- 即 x − x 0 cos α \frac{x-x_0}{\cos{\alpha}} cosαx−x0= y − y 0 sin α \frac{y-y_0}{\sin{\alpha}} sinαy−y0,令其比值为参数 t t t,即有
- x − x 0 = t cos α x-x_0=t\cos\alpha x−x0=tcosα, y − y 0 y-y_0 y−y0= t sin α t\sin\alpha tsinα
- 这里的参数 t t t有明显的几何意义: ∣ t ∣ |t| ∣t∣表示直线上的任一点 M M M到定点 M 0 M_0 M0的距离
- 整理:得方程组
(2)参数 t ∈ R t\in{\mathbb{R}} t∈R,- x = x 0 + t cos α x=x_0+t\cos{\alpha} x=x0+tcosα;
- y = y 0 + t sin α y=y_0+t\sin\alpha y=y0+tsinα
向量法
-
设直线过点 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0),且与平面向量 a = ( l , m ) \bold{a}=(l,m) a=(l,m)平行 ( l , m ≠ 0 ) (l,m\neq{0}) (l,m=0),
-
在直线上任取点 M ( x , y ) M(x,y) M(x,y),则向量 M 0 M → / / a \overrightarrow{M_0M}//\bold{a} M0M//a, M 0 M → \overrightarrow{M_0M} M0M= ( x − x 0 , y − y 0 ) (x-x_0,y-y_0) (x−x0,y−y0)
-
两向量平行的充要条件是 x − x 0 l = y − y 0 m \frac{x-x_0}{l}=\frac{y-y_0}{m} lx−x0=my−y0,记该比值式比值为 t t t,
-
整理得方程组
(3)- x = x 0 + l t x=x_0+lt x=x0+lt,
- y = y 0 + m t y=y_0+mt y=y0+mt,
- 参数 t ∈ R t\in\mathbb{R} t∈R
参数方程间的转换
从第3型转化为第2型方程组
-
方法1:
-
设(3)转换的第2型方程组为
- x = x 0 + u cos α x=x_0+u\cos\alpha x=x0+ucosα
- y = y 0 + u sin α y=y_0+u\sin\alpha y=y0+usinα
-
和(3)比较可知, u cos α = l t u\cos\alpha=lt ucosα=lt; u sin α = m t u\sin\alpha=mt usinα=mt,则 tan α = m l \tan{\alpha}=\frac{m}{l} tanα=lm
-
只要求出 cos α \cos\alpha cosα, sin α \sin\alpha sinα关于 l , m l,m l,m的表示式即可:
-
cos α \cos\alpha cosα= ± l m 2 + l 2 \pm{\frac{l}{\sqrt{m^2+l^2}}} ±m2+l2l
-
sin α = ± m m 2 + l 2 \sin\alpha=\pm\frac{m}{\sqrt{m^2+l^2}} sinα=±m2+l2m
-
根据 α \alpha α的来取定两个式子的符号:
-
cos α = l m 2 + l 2 \cos\alpha=\frac{l}{\sqrt{m^2+l^2}} cosα=m2+l2l
-
sin α = m m 2 + l 2 \sin\alpha=\frac{m}{\sqrt{m^2+l^2}} sinα=m2+l2m
-
-
-
方法2:
- 由于2型方程中的 α \alpha α是直线的倾斜角,因此,根据直线某个同向方向向量 ( l , m ) (l,m) (l,m)可得
- l 1 l_1 l1: cos α = l m 2 + l 2 \cos\alpha=\frac{l}{\sqrt{m^2+l^2}} cosα=m2+l2l; sin α = m m 2 + l 2 \sin\alpha=\frac{m}{\sqrt{m^2+l^2}} sinα=m2+l2m
- l 2 l_2 l2: cos α = − l m 2 + l 2 \cos\alpha=-\frac{l}{\sqrt{m^2+l^2}} cosα=−m2+l2l; sin α = − m m 2 + l 2 \sin\alpha=-\frac{m}{\sqrt{m^2+l^2}} sinα=−m2+l2m
- 两组都可以:验证:
- l 1 l_1 l1: x = x 0 + t cos α x=x_0+t\cos{\alpha} x=x0+tcosα; y = y 0 + t sin α y=y_0+t\sin\alpha y=y0+tsinα
- l 2 l_2 l2: x = x 0 − t cos α x=x_0-t\cos{\alpha} x=x0−tcosα; y = y 0 − t sin α y=y_0-t\sin\alpha y=y0−tsinα
- 当 t = 1 t=1 t=1时 ( x 0 + cos α , y 0 + sin α ) (x_0+\cos\alpha,y_0+\sin\alpha) (x0+cosα,y0+sinα)和 t = − 1 t=-1 t=−1时 ( x 0 − cos α , y 0 − sin α ) (x_0-\cos\alpha,y_0-\sin\alpha) (x0−cosα,y0−sinα)都同时在 l 1 , l 2 l_1,l_2 l1,l2上,说明 l 1 , l 2 l_1,l_2 l1,l2是同一条直线
- 或者分别将 l 1 l_1 l1, l 2 l_2 l2化为普通方程,可得相同的直角坐标方程: y − y 0 x − x 0 = tan α \frac{y-y_0}{x-x_0}=\tan{\alpha} x−x0y−y0=tanα
例
-
设直线 x = 5 + 3 t x=5+3t x=5+3t; y = 10 − 4 t y=10-4t y=10−4t;将其表示为第2形式参数方程
-
从第3型转化为第2型:
- cos α = 3 3 2 + 4 2 \cos\alpha=\frac{3}{\sqrt{3^2+4^2}} cosα=32+423= 3 5 \frac{3}{5} 53; sin α \sin\alpha sinα= − 4 3 2 + 4 2 \frac{-4}{\sqrt{3^2+4^2}} 32+42−4= − 4 5 -\frac{4}{5} −54
- 另一组取值 cos α = − 3 5 \cos\alpha=-\frac{3}{5} cosα=−53, sin α = 4 5 \sin\alpha=\frac{4}{5} sinα=54也可以
- 两组取值都有( tan α = − 4 3 \tan\alpha=-\frac{4}{3} tanα=−34)
- 所以
- x = 5 + 3 5 u x=5+\frac{3}{5}u x=5+53u; y = 10 − 4 5 u y=10-\frac{4}{5}u y=10−54u
- x = 5 − 3 5 u x=5-\frac{3}{5}u x=5−53u; y = 10 + 4 5 u y=10+\frac{4}{5}u y=10+54u
相关文章:

EM@直线的参数方程
文章目录 abstract直线参数方程从运动轨迹的角度从普通方程转换导参数方程向量法 参数方程间的转换从第3型转化为第2型方程组例 abstract 平面直线的参数方程的3种表示形式直线参数方程间的转换 直线参数方程 以下从不同角度推导直线参数方程分别记为第1,2,3形式参数方程 从…...

day08-注册功能、前端登录注册页面复制、前端登录功能、前端注册功能
1 注册功能 补充(开放文件夹内) 2 前端登录注册页面复制 4 前端注册功能 1 注册功能 # 分析前端:携带数据格式 {mobile:,code:,password}后端:-1 视图类---》注册方法-2 序列化类---》校验,保存(表中字段多,传的少---…...
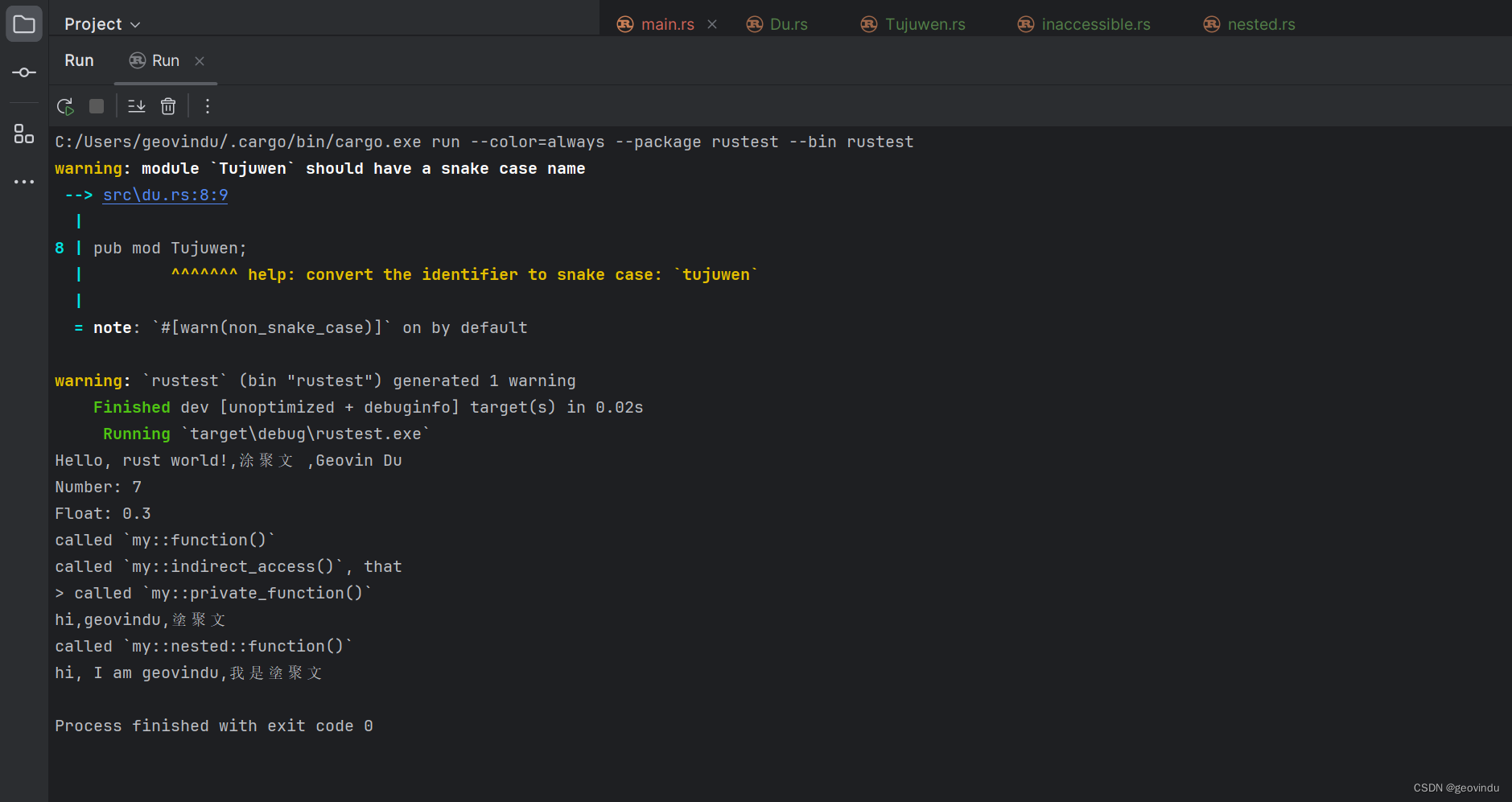
rust: function
///file: nestd.rs ///ide: RustRover 233.8264.22 /// /// /// /***自定义函数*/ pub fn function() {println!("called my::nested::function()"); }#[allow(dead_code)] fn private_function() {println!("called my::nested::private_function()"); }/…...
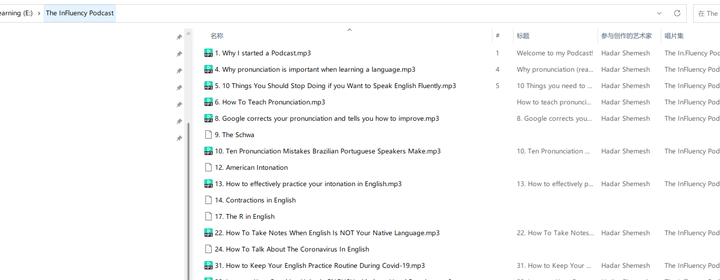
零代码编程:用ChatGPT批量下载谷歌podcast上的播客音频
谷歌podcast有很多播客音频,如何批量下载到电脑呢? 以这个播客为例: https://podcasts.google.com/feed/aHR0cHM6Ly9oYWRhcnNoZW1lc2guY29tL2ZlZWQvcG9kY2FzdC8?saX&ved0CAkQlvsGahcKEwi4uauWsvKBAxUAAAAAHQAAAAAQAg 查看网页源代码&a…...
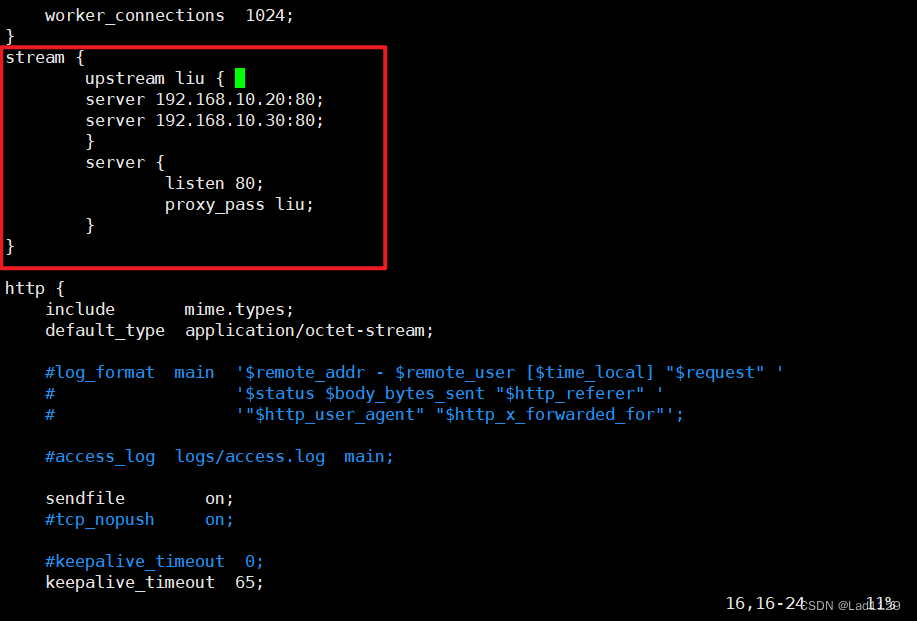
nginx.4——正向代理和反向代理(七层代理和四层代理)
1、正向代理反向代理 nginx当中有两种代理方式 七层代理(http协议) 四层代理(tcp/udp流量转发) 七层代理 七层代理:代理的是http的请求和响应。 客户端请求代理服务器,由代理服务器转发给客户端http请求。转发到内部服务器(可以单台&#…...
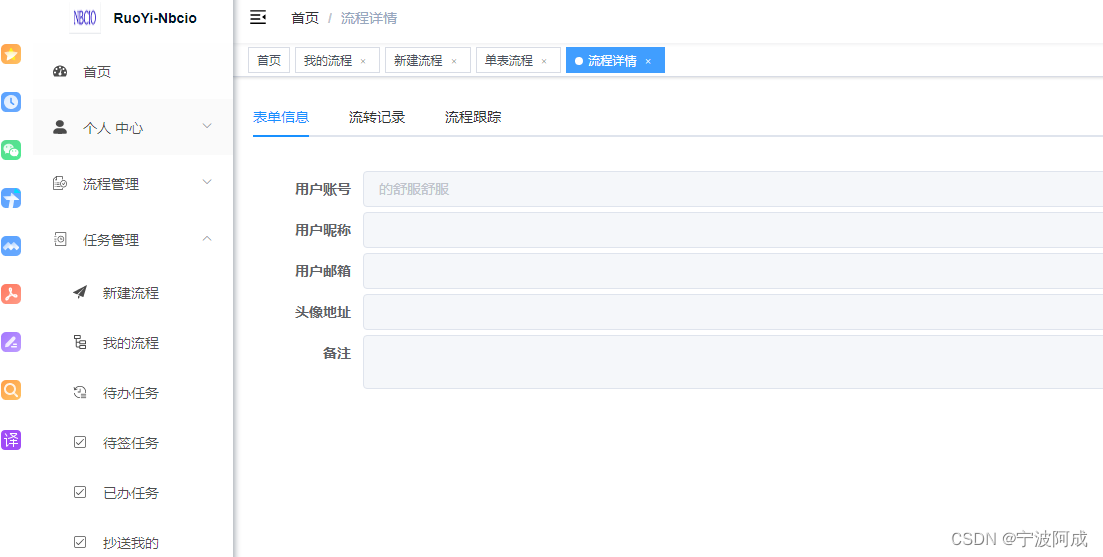
基于RuoYi-Flowable-Plus的若依ruoyi-nbcio支持自定义业务表单流程(三)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 相应的后端也要做一些调整 1、启动流程修改如下: /*** 启动流程实例*/private R startProce…...
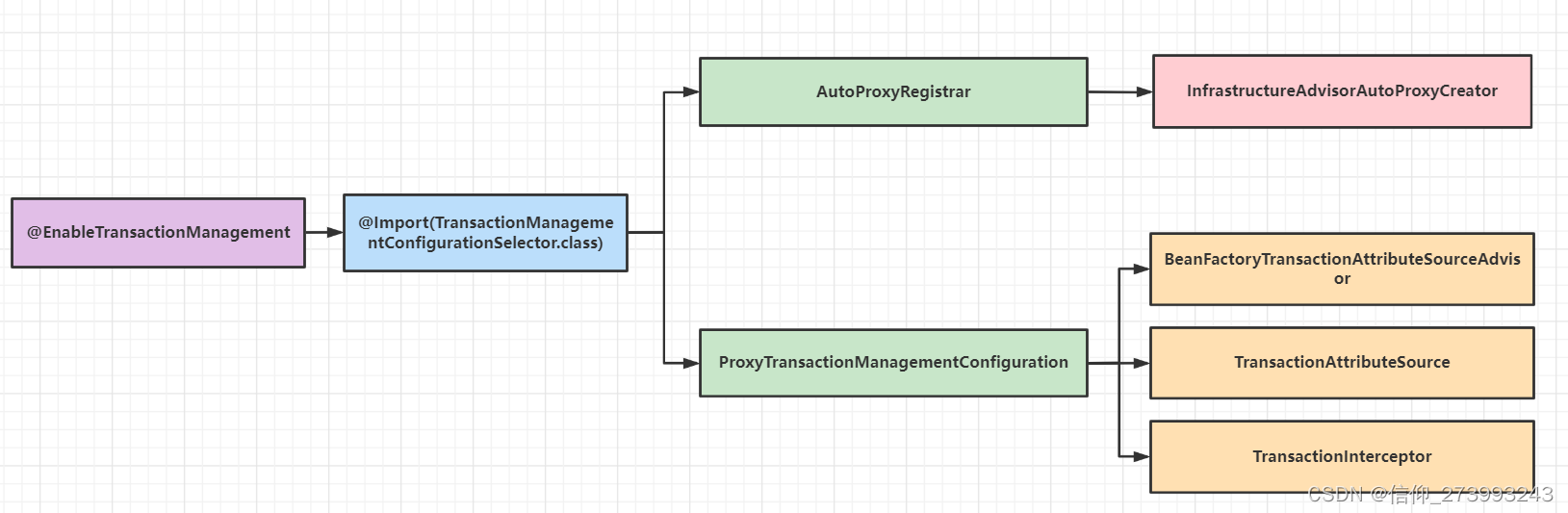
Spring-事务源码解析2
上一篇文章我们介绍了事务开启注解EnableTransactionManagement源码解析《Spring-事务源码解析1》 里面提到了2个关键组件,这里我们分析下Spring如何利用这2个组件来给Bean创建代理对象。 本篇文章我们看下当一个类里面包含了Transactional注解,Spring如…...
基于ssm008医院门诊挂号系统+jsp【附PPT|开题|任务书|万字文档(LW)和搭建文档】
主要功能 后台登录:4个角色 管理员: ①个人中心、修改密码、个人信息 ②药房管理、护士管理、医生管理、病人信息管理、科室信息管理、挂号管理、诊断信息管理、病例库管理、开药信息管理、药品信息管理、收费信息管理 药房: ①个人中心、修…...

【Linux常用命令11】Linux文件与权限详解
权限 r :读权限,用数字4表示 w :写权限,用数字2表示 x :执行权限,用数字1表示 常用权限 644:代表所有者拥有读、写权限,而所属组和其他人拥有只读权限。 755:代表所有…...

BAT026:删除当前目录指定文件夹以外的文件夹
引言:编写批处理程序,实现删除当前目录指定文件夹以外的文件夹。 一、新建Windows批处理文件 参考博客: CSDNhttps://mp.csdn.net/mp_blog/creation/editor/132137544 二、写入批处理代码 1.右键新建的批处理文件,点击【编辑】…...

Python浏览器自动化
如果你正在进行手机爬虫的工作,并且希望通过模拟浏览器行为来抓取数据,那么Pyppeteer将会是你的理想选择。Pyppeteer是一个强大的Python库,它可以让你控制浏览器进行自动化操作,如点击按钮、填写表单等,从而实现数据的…...
基于tornado BELLE 搭建本地的web 服务
我的github 将BELLE 封装成web 后端服务,采用tornado 框架 import timeimport torch import torch.nn as nnfrom gptq import * from modelutils import * from quant import *from transformers import AutoTokenizer import sys import json #import lightgbm a…...

信息系统漏洞与风险管理制度
1、总则 1.1、目的 为了进一步规范XXXXX单位信息系统风险管理活动,提升风险管理工作的可操纵性和适用性,使信息网络正常运行,防止网络攻击,保证业务的正常进行,依据XXXXX单位员的相关规范和标准规定,特制…...
:MapReduce之ReduceJoin案例分析)
Hadoop3教程(十七):MapReduce之ReduceJoin案例分析
文章目录 (113)ReduceJoin案例需求分析(114)ReduceJoin案例代码实操 - TableBean(115)ReduceJoin案例代码实操 - TableMapper(116)ReduceJoin案例代码实操 - Reducer及Driver参考文献…...
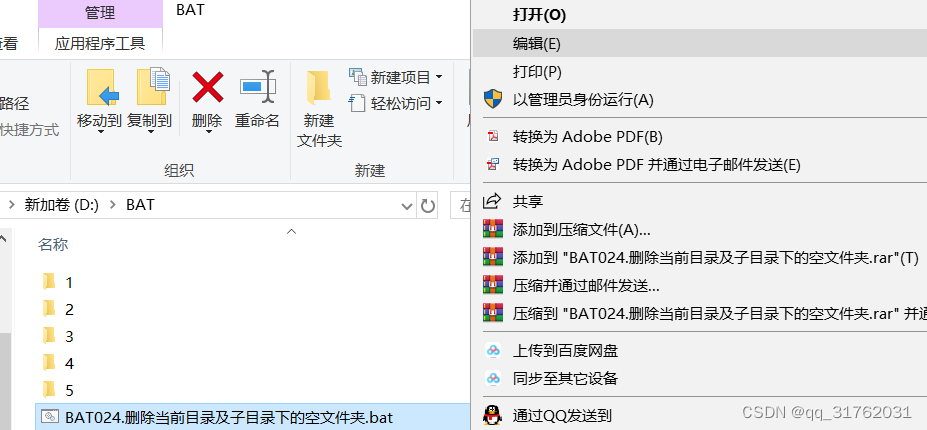
BAT026:删除当前目录及子目录下的空文件夹
引言:编写批处理程序,实现批量删除当前目录及子目录下的空文件夹。 一、新建Windows批处理文件 参考博客: CSDNhttps://mp.csdn.net/mp_blog/creation/editor/132137544 二、写入批处理代码 1.右键新建的批处理文件,点击【编辑…...

nodejs+vue网课学习平台
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

Can Language Models Make Fun? A Case Study in Chinese Comical Crosstalk
本文是LLM系列文章,针对《Can Language Models Make Fun? A Case Study in Chinese Comical Crosstalk》的翻译。 语言模型能制造乐趣吗?中国滑稽相声个案研究 摘要1 引言2 问题定义3 数据集4 使用自动评估生成基准5 人工评估6 讨论7 结论与未来工作 摘要 语言是…...
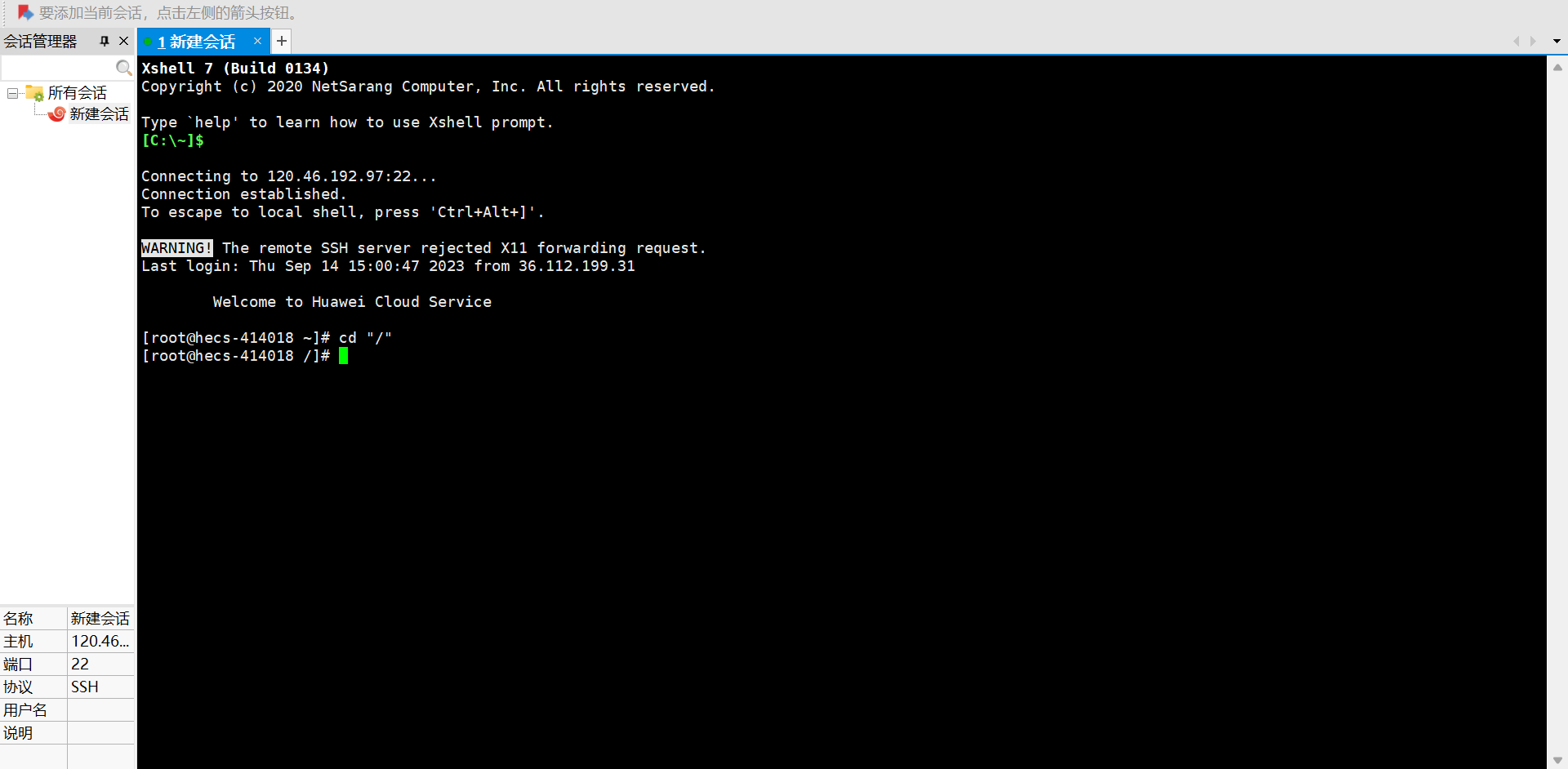
阿里云云服务器实例使用教学
目录 云服务器免费试用 详细步骤 Xshell 远程连接 云服务器免费试用 阿里云云服务器网址:阿里云免费试用 - 阿里云 详细步骤 访问阿里云免费试用。单击页面右上方的登录/注册按钮,并根据页面提示完成账号登录(已有阿里云账号)…...

promisify 是 Node.js 标准库 util 模块中的一个函数
promisify 是 Node.js 标准库 util 模块中的一个函数。它用于将遵循 Node.js 回调风格的函数转换为返回 Promise 的函数。这使得你可以使用 async/await 语法来等待异步操作完成,从而让异步代码看起来更像同步代码。 在 Node.js 的回调风格中,函数通常接…...

ArcGIS在VUE框架中的构建思想
项目快要上线了,出乎意料的有些空闲时间。想着就把其他公司开发的一期代码里面,把关于地图方面的代码给优化一下。试运行的时候,客户说控制台有很多飘红的报错,他们很在意,虽然很不情愿,但能改的就给改了吧…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
