(五)物质导数与空间时间导数
本文内容主要包括:
1. 物质导数与空间时间导数及二者的联系
考虑运动变形过程中代表性物质点的物理量 Φ\bold\PhiΦ(张量) 随时间的变化率。
- 在物质描述中,Φ\bold\PhiΦ 以 (X⃗,t)(\vec{X},t)(X,t) 为自变量;
- 在空间描述中,Φ\bold\PhiΦ 以 (x⃗,t)(\vec{x},t)(x,t) 为自变量。
物理量 Φ\bold \PhiΦ 随某一固定的物质点一起运动的时间变化率(称作:物质导数)可写作:
DΦDt=(∂Φ(X⃗,t)∂t)∣X⃗≜Φ∙\dfrac{D\bold \Phi}{Dt} =\left. \left(\frac{\partial \bold\Phi(\vec{X},t)}{\partial t}\right)\right|_{\vec X} \triangleq \overset{\bullet}{\bold\Phi}DtDΦ=(∂t∂Φ(X,t))X≜Φ∙
物理量 Φ\bold \PhiΦ 在某一固定的空间坐标上的时间变化率(称作:空间时间导数/局部导数)可写作:
(∂Φ(x⃗,t)∂t)∣x⃗≜Φ′\left. \left(\frac{\partial \bold\Phi(\vec{x},t)}{\partial t}\right)\right|_{\vec x} \triangleq \bold\Phi'(∂t∂Φ(x,t))x≜Φ′
根据复合函数的求导法则可推出:
Φ∙={∂Φ[x⃗(X⃗,t),t]∂t}∣X⃗=(∂Φ∂t)∣x⃗+(∂Φ∂xr)(∂xr∂t)∣X⃗=Φ′+(∂Φ∂xr⊗g⃗r)⋅(g⃗s∂xs∂t)∣X⃗=Φ′+(Φ▽)⋅(∂x⃗∂t)∣X⃗=Φ′+(Φ▽)⋅(∂u⃗∂t)=Φ′+(Φ▽)⋅v⃗=Φ′+v⃗⋅(▽Φ)\begin{aligned} & \overset{\bullet}{\bold\Phi} =\left. \left\{\frac{\partial \bold\Phi[\vec{x}(\vec{X},t),t]}{\partial t}\right\}\right|_{\vec X} \\\\ &\quad=\left.\left(\dfrac{\partial\bold\Phi}{\partial t}\right)\right|_{\vec{x}}+\left(\dfrac{\partial\bold\Phi}{\partial {x}^r}\right)\left.\left(\dfrac{\partial x^r}{\partial t}\right)\right|_{\vec{X}}\\\\ &\quad=\bold\Phi'+\left(\dfrac{\partial\bold\Phi}{\partial {x}^r}\otimes\vec{g}\ ^r\right)\cdot\left.\left(\vec{g}_s\dfrac{\partial x^s}{\partial t}\right)\right|_{\vec{X}}\\\\ &\quad=\bold\Phi'+\left(\bold\Phi\triangledown\right)\cdot\left.\left(\dfrac{\partial\vec x}{\partial t}\right)\right|_{\vec{X}}\\\\ &\quad=\bold\Phi'+\left(\bold\Phi\triangledown\right)\cdot\left(\dfrac{\partial\vec u}{\partial t}\right)\\\\ &\quad=\bold\Phi'+\left(\bold\Phi\triangledown\right)\cdot\vec{v}\\\\ &\quad=\bold\Phi'+\vec{v}\cdot\left(\triangledown\bold\Phi\right) \end{aligned}Φ∙={∂t∂Φ[x(X,t),t]}X=(∂t∂Φ)x+(∂xr∂Φ)(∂t∂xr)X=Φ′+(∂xr∂Φ⊗g r)⋅(gs∂t∂xs)X=Φ′+(Φ▽)⋅(∂t∂x)X=Φ′+(Φ▽)⋅(∂t∂u)=Φ′+(Φ▽)⋅v=Φ′+v⋅(▽Φ)
2. 空间坐标系相关量的物质导数
2.1. 空间坐标系基矢的物质导数
随时间变化,某一固定物质点将映射至空间坐标系中的不同位置。因此,“空间坐标系基矢的物质导数”是指:某一物质点所在处的基矢变化率。故
g⃗i∙=(g⃗i)′+v⃗⋅▽g⃗i=v⃗⋅▽g⃗i=vj∂g⃗i∂xj=vjΓijkg⃗k=vjΓij,kg⃗k\overset{\bullet}{\vec{g}_i} =(\vec{g}_i)'+\vec{v}\cdot\triangledown\vec{g}_i =\vec{v}\cdot\triangledown\vec{g}_i =v^j\dfrac{\partial \vec{g}_i}{\partial x^j} =v^j\Gamma_{ij}^k\vec{g}_k =v^j\Gamma_{ij,k}\vec{g}^kgi∙=(gi)′+v⋅▽gi=v⋅▽gi=vj∂xj∂gi=vjΓijkgk=vjΓij,kgk
式中,Γijk、Γij,k\Gamma_{ij}^k、\Gamma_{ij,k}Γijk、Γij,k 分别为空间坐标系的第二类、第一类 Christoffel 符号。又由于
DDt(g⃗i⋅g⃗j)=g⃗i∙⋅g⃗j+g⃗i⋅g⃗j∙=0⟹g⃗i⋅g⃗j∙=−g⃗i∙⋅g⃗j\dfrac{D}{Dt}(\vec{g}_i\cdot\vec{g}^j) =\overset{\bullet}{\vec{g}_i}\cdot\vec{g}^j+\vec{g}_i\cdot\overset{\bullet}{\vec{g}^j} =0 \Longrightarrow \vec{g}_i\cdot\overset{\bullet}{\vec{g}^j}=-\overset{\bullet}{\vec{g}_i}\cdot\vec{g}^jDtD(gi⋅gj)=gi∙⋅gj+gi⋅gj∙=0⟹gi⋅gj∙=−gi∙⋅gj
令 g⃗j∙=βijg⃗i\overset{\bullet}{\vec{g}^j}=\beta^j_i\vec{g}^igj∙=βijgi ,那么:
g⃗i⋅βkjg⃗k=βij=−g⃗i∙⋅g⃗j=−vkΓikj\vec{g}_i\cdot\beta^j_k\vec{g}^k =\beta^j_i =-\overset{\bullet}{\vec{g}_i}\cdot\vec{g}^j =-v^k\Gamma^j_{ik}gi⋅βkjgk=βij=−gi∙⋅gj=−vkΓikj
故,
g⃗j∙=−vkΓikjg⃗i\overset{\bullet}{\vec{g}^j}=-v^k\Gamma^j_{ik}\vec{g}^igj∙=−vkΓikjgi
2.2. 空间坐标系协变基矢混合积的 g\sqrt{g}g 的物质导数
由空间坐标系基矢的物质导数可知:
gij∙=g⃗i∙⋅g⃗j+g⃗i⋅g⃗j∙=vr(Γirkgkj+Γjrkgki)=vr(Γir,j+Γjr,i)\overset{\bullet}{g_{ij}} =\overset{\bullet}{\vec{g}_i}\cdot\vec{g}_j+\vec{g}_i\cdot\overset{\bullet}{\vec{g}_j} =v^r(\Gamma^k_{ir}g_{kj}+\Gamma^k_{jr}g_{ki}) =v^r(\Gamma_{ir,j}+\Gamma_{jr,i})gij∙=gi∙⋅gj+gi⋅gj∙=vr(Γirkgkj+Γjrkgki)=vr(Γir,j+Γjr,i)
由于,
1det([A])[A∗]=[A]−1\dfrac{1}{det([A])}[A^*]=[A]^{-1}det([A])1[A∗]=[A]−1
其中,[A∗][A^*][A∗] 为 [A][A][A] 的伴随矩阵。则
1g∂g∂gji=gij,g=det(gij)\dfrac{1}{g}\dfrac{\partial g}{\partial g_{ji}}=g^{ij},g=det(g_{ij})g1∂gji∂g=gij,g=det(gij)
故,det(gij)det(g_{ij})det(gij) 的物质导数为:
g∙=∂g∂gjigji∙=ggijgji∙=gvr(Γiri+Γjrj)=2gvrΓiri\overset{\bullet}{g} =\dfrac{\partial g}{\partial g_{ji}}\overset{\bullet}{g_{ji}} =gg^{ij}\overset{\bullet}{g_{ji}} =gv^r(\Gamma_{ir}^i+\Gamma_{jr}^j) =2gv^r\Gamma_{ir}^ig∙=∂gji∂ggji∙=ggijgji∙=gvr(Γiri+Γjrj)=2gvrΓiri
式中,Γiri\Gamma_{ir}^iΓiri 为空间坐标系的第二类Christoffel 符号。进一步:
g∙=gvrΓiri\overset{\bullet}{\sqrt{g}}=\sqrt gv^r\Gamma_{ir}^ig∙=gvrΓiri
上式也可利用第二类Christoffel符号与协变基矢的混合积 g\sqrt{g}g 的关系与物质导数和局部导数的关系得到:
g∙=v⃗⋅(▽g)=vi∂g∂xi=gvrΓiri\overset{\bullet}{\sqrt{g}} =\vec{v}\cdot(\triangledown\sqrt{g}) =v^i\dfrac{\partial \sqrt{g}}{\partial x^i} =\sqrt gv^r\Gamma_{ir}^ig∙=v⋅(▽g)=vi∂xi∂g=gvrΓiri
3. 随体坐标系 {XA,t}\{X^A,t\}{XA,t} 相关量的物质导数
3.1. 随体坐标系 {XA,t}\{X^A,t\}{XA,t} 基矢的物质导数
随时间的变化,特定的物质点在随体坐标系 {XA,t}\{X^A,t\}{XA,t} 中的基矢不断改变。其协变基矢的变化率可写作:
C⃗A∙=[∂∂t(∂x⃗∂XA)]∣X⃗=[∂∂XA(∂x⃗∂t)]∣X⃗=∂∂XA(∂u⃗∂t)=∂v⃗∂XA=vB∣∣AC⃗B=∂v⃗∂xi∂xi∂XA=x,Ai∂v⃗∂xi=x,Aivj∣ig⃗j\begin{aligned} &\overset{\bullet}{\vec{C}_A} =\left.\left[\dfrac{\partial}{\partial t}\left(\dfrac{\partial \vec{x}}{\partial X^A}\right)\right]\right|_{\vec{X}} =\left.\left[\dfrac{\partial}{\partial X^A}\left(\dfrac{\partial \vec{x}}{\partial t}\right)\right]\right|_{\vec{X}} \\\ \\ &\quad\ =\dfrac{\partial}{\partial X^A}\left(\dfrac{\partial \vec{u}}{\partial t}\right) =\dfrac{\partial\vec{v}}{\partial X^A} =v^B||_A\vec{C}_B \\\ \\ &\quad\ =\dfrac{\partial\vec{v}}{\partial x^i}\dfrac{\partial x^i}{\partial X^A} =x^i_{,A}\dfrac{\partial\vec{v}}{\partial x^i} =x^i_{,A}v^j|_i\vec{g}_j \end{aligned} CA∙=[∂t∂(∂XA∂x)]X=[∂XA∂(∂t∂x)]X =∂XA∂(∂t∂u)=∂XA∂v=vB∣∣ACB =∂xi∂v∂XA∂xi=x,Ai∂xi∂v=x,Aivj∣igj
同理可知
C⃗A∙∙=∂a⃗∂XA=aB∣∣AC⃗B\overset{\bullet\bullet}{\vec{C}_A} =\dfrac{\partial\vec{a}}{\partial X^A} =a^B||_A\vec{C}_BCA∙∙=∂XA∂a=aB∣∣ACB
又
DC⃗A⋅C⃗BDt=C⃗A∙⋅C⃗B+C⃗A⋅C⃗B∙=0\dfrac{D{\vec{C}_A\cdot\vec{C}^B}}{Dt} =\overset{\bullet}{\vec{C}_A}\cdot\vec{C}^B+{\vec{C}_A}\cdot\overset{\bullet}{\vec{C}^B} =0DtDCA⋅CB=CA∙⋅CB+CA⋅CB∙=0
故
C⃗A∙=−(C⃗B∙⋅C⃗A)C⃗B=−vA∣∣BC⃗B=−X,jAvj∣ig⃗i\overset{\bullet}{\vec{C}^A} =-(\overset{\bullet}{\vec{C}_B}\cdot\vec{C}^A)\vec{C}^B =-v^A||_B\vec{C}^B =-X^A_{,\ j}v^j|_i\vec{g}^iCA∙=−(CB∙⋅CA)CB=−vA∣∣BCB=−X, jAvj∣igi
3.2. 随体坐标系 {XA,t}\{X^A,t\}{XA,t} 协变基矢混合积的 C\sqrt{C}C 的物质导数
C∙AB=C⃗∙A⋅C⃗B+C⃗A⋅C⃗∙B=vB∣∣A+vA∣∣B\overset{\bullet}{C}_{AB} =\overset{\bullet}{\vec C}_{A}\cdot{\vec C}_{B}+\vec{C}_A\cdot\overset{\bullet}{\vec C}_{B} =v_B||_A+v_A||_BC∙AB=C∙A⋅CB+CA⋅C∙B=vB∣∣A+vA∣∣B
又
1C∂C∂CBA=C−1AB,C=det(CAB)\dfrac{1}{C}\dfrac{\partial C}{\partial C_{BA}}=\overset{-1}{C}\ ^{AB},C=det(C_{AB})C1∂CBA∂C=C−1 AB,C=det(CAB)
则
C∙=∂C∂CBAC∙AB=CC−1ABC∙AB=C(vA∣∣A+vB∣∣B)=2CvA∣∣A\overset{\bullet}{C} =\dfrac{\partial C}{\partial C_{BA}}\overset{\bullet}{C}_{AB} =C\overset{-1}{C}\ ^{AB}\overset{\bullet}{C}_{AB} =C(v^A||_A+v^B||_B) =2Cv^A||_AC∙=∂CBA∂CC∙AB=CC−1 ABC∙AB=C(vA∣∣A+vB∣∣B)=2CvA∣∣A
进一步知:
C∙=12CC∙=CvA∣∣A\overset{\bullet}{\sqrt C} =\dfrac{1}{2\sqrt C}\overset{\bullet}{C} =\sqrt Cv^A||_AC∙=2C1C∙=CvA∣∣A
3.3. J\mathscr{J}J 的物质导数
由于,
J=det(F)=CG\mathscr{J}=det(\bold F)=\sqrt{\dfrac{C}{G}}J=det(F)=GC
故,
J∙=C∙G=CGvA∣∣A=JvA∣∣A=J▽⋅v⃗\overset{\bullet}{\mathscr{J}} ={\dfrac{\overset{\bullet}{\sqrt C}}{\sqrt G}} =\dfrac{\sqrt C}{\sqrt G}v^A||_A =\mathscr{J}v^A||_A =\mathscr{J}\triangledown\cdot\vec{v}J∙=GC∙=GCvA∣∣A=JvA∣∣A=J▽⋅v
4. 任意张量在空间坐标系与随体坐标系 {XA,t}\{X^A,t\}{XA,t} 中的物质导数
以三阶张量为例:
Φ=Φ∙∙kijg⃗i⊗g⃗j⊗g⃗k=Φ∙∙MABC⃗A⊗C⃗B⊗C⃗M\bold\Phi =\varPhi^{ij}_{\bullet\bullet k}\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k =\varPhi^{AB}_{\bullet\bullet M}\ \vec{C}_A\otimes\vec{C}_B\otimes\vec{C}^MΦ=Φ∙∙kij gi⊗gj⊗gk=Φ∙∙MAB CA⊗CB⊗CM
则
Φ∙=Φ∙∙∙MABC⃗A⊗C⃗B⊗C⃗M+Φ∙∙MABC⃗A∙⊗C⃗B⊗C⃗M+Φ∙∙MABC⃗A⊗C⃗B∙⊗C⃗M+Φ∙∙MABC⃗A⊗C⃗B⊗C⃗∙M=(Φ∙∙∙MAB+Φ∙∙MNBvA∣∣N+Φ∙∙MANvB∣∣N−Φ∙∙NABvN∣∣M)C⃗A⊗C⃗B⊗C⃗M\begin{aligned} &\overset{\bullet}{\bold\Phi} =\overset{\bullet}{\varPhi}\ ^{AB}_{\bullet\bullet M}\ \vec{C}_A\otimes\vec{C}_B\otimes\vec{C}^M +\varPhi^{AB}_{\bullet\bullet M}\ \overset{\bullet}{\vec{C}_A}\otimes\vec{C}_B\otimes\vec{C}^M +\varPhi^{AB}_{\bullet\bullet M}\ \vec{C}_A\otimes\overset{\bullet}{\vec{C}_B}\otimes\vec{C}^M +\varPhi^{AB}_{\bullet\bullet M}\ \vec{C}_A\otimes\vec{C}_B\otimes\overset{\bullet}{\vec{C}}\ ^M \\\\ &\ \ \ =(\overset{\bullet}{\varPhi}\ ^{AB}_{\bullet\bullet M}+\varPhi^{NB}_{\bullet\bullet M}\ v^A||_N+\varPhi^{AN}_{\bullet\bullet M}\ v^B||_N-\varPhi^{AB}_{\bullet\bullet N}\ v^N||_M)\ \vec{C}_A\otimes\vec{C}_B\otimes\vec{C}^M \end{aligned}Φ∙=Φ∙ ∙∙MAB CA⊗CB⊗CM+Φ∙∙MAB CA∙⊗CB⊗CM+Φ∙∙MAB CA⊗CB∙⊗CM+Φ∙∙MAB CA⊗CB⊗C∙ M =(Φ∙ ∙∙MAB+Φ∙∙MNB vA∣∣N+Φ∙∙MAN vB∣∣N−Φ∙∙NAB vN∣∣M) CA⊗CB⊗CM
或
Φ∙=Φ∙∙∙kijg⃗i⊗g⃗j⊗g⃗k+Φ∙∙kijg⃗∙i⊗g⃗j⊗g⃗k+Φ∙∙kijg⃗i⊗g⃗∙j⊗g⃗k+Φ∙∙kijg⃗i⊗g⃗j⊗g⃗∙k=(Φ∙∙∙kij+Φ∙∙ksjvrΓrsi+Φ∙∙kisvrΓrsj−Φ∙∙sijvrΓrks)g⃗i⊗g⃗j⊗g⃗k=[(Φ∙∙kij)′+(vrΦ∙∙k,rij+Φ∙∙ksjvrΓrsi+Φ∙∙kisvrΓrsj−Φ∙∙sijvrΓrks)]g⃗i⊗g⃗j⊗g⃗k=[(Φ∙∙kij)′+vrΦ∙∙kij∣r)]g⃗i⊗g⃗j⊗g⃗k=Φ′+v⃗⋅▽Φ\begin{aligned} &\overset{\bullet}{\bold\Phi} =\overset{\bullet}{\varPhi}\ ^{ij}_{\bullet\bullet k}\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k +\varPhi^{ij}_{\bullet\bullet k}\ \overset{\bullet}{\vec{g}}_i\otimes\vec{g}_j\otimes\vec{g}^k +\varPhi^{ij}_{\bullet\bullet k}\ \vec{g}_i\otimes\overset{\bullet}{\vec{g}}_j\otimes\vec{g}^k +\varPhi^{ij}_{\bullet\bullet k}\ \vec{g}_i\otimes\vec{g}_j\otimes\overset{\bullet}{\vec{g}}\ ^k \\\\ &\ \ \ =(\overset{\bullet}{\varPhi}\ ^{ij}_{\bullet\bullet k}+{\varPhi}\ ^{sj}_{\bullet\bullet k}v^r\Gamma^i_{rs}+{\varPhi}\ ^{is}_{\bullet\bullet k}v^r\Gamma^j_{rs}-{\varPhi}\ ^{ij}_{\bullet\bullet s}v^r\Gamma^s_{rk})\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k \\\\ &\ \ \ =[({\varPhi}\ ^{ij}_{\bullet\bullet k})'+(v^r{\varPhi}\ ^{ij}_{\bullet\bullet k,r}+{\varPhi}\ ^{sj}_{\bullet\bullet k}v^r\Gamma^i_{rs}+{\varPhi}\ ^{is}_{\bullet\bullet k}v^r\Gamma^j_{rs}-{\varPhi}\ ^{ij}_{\bullet\bullet s}v^r\Gamma^s_{rk})]\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k \\\\ &\ \ \ =[({\varPhi}\ ^{ij}_{\bullet\bullet k})'+v^r{\varPhi}\ ^{ij}_{\bullet\bullet k}|_r)]\ \vec{g}_i\otimes\vec{g}_j\otimes\vec{g}^k \\\\ &\ \ \ =\bold\Phi'+\vec{v}\cdot\triangledown\bold\Phi \end{aligned}Φ∙=Φ∙ ∙∙kij gi⊗gj⊗gk+Φ∙∙kij g∙i⊗gj⊗gk+Φ∙∙kij gi⊗g∙j⊗gk+Φ∙∙kij gi⊗gj⊗g∙ k =(Φ∙ ∙∙kij+Φ ∙∙ksjvrΓrsi+Φ ∙∙kisvrΓrsj−Φ ∙∙sijvrΓrks) gi⊗gj⊗gk =[(Φ ∙∙kij)′+(vrΦ ∙∙k,rij+Φ ∙∙ksjvrΓrsi+Φ ∙∙kisvrΓrsj−Φ ∙∙sijvrΓrks)] gi⊗gj⊗gk =[(Φ ∙∙kij)′+vrΦ ∙∙kij∣r)] gi⊗gj⊗gk =Φ′+v⋅▽Φ
相关文章:
物质导数与空间时间导数)
(五)物质导数与空间时间导数
本文内容主要包括:1. 物质导数与空间时间导数及二者的联系2. 空间坐标系相关量的物质导数2.1. 空间坐标系基矢的物质导数2.2. 空间坐标系协变基矢混合积的 g\sqrt{g}g 的物质导数3. 随体坐标系 {XA,t}\{X^A,t\}{XA,t} 相关量的物质导数3.1. 随体坐标系 {XA,t}\{X^…...
)
python实战应用讲解-【语法基础篇】流程控制-运算符(附示例代码)
目录 比较运算符 相等运算符 is:相同运算符 in:成员资格运算符 字符串和序列的比较...
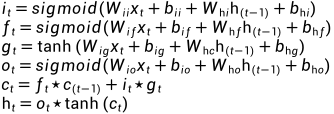
MXNet中使用双向循环神经网络BiRNN对文本进行情感分类
文本分类类似于图片分类,也是很常见的一种分类任务,将一段不定长的文本序列变换为文本的类别。这节主要就是关注文本的情感分析(sentiment analysis),对电影的评论进行一个正面情绪与负面情绪的分类。整理数据集第一步都是将数据集整理好&…...

SpringBoot 整合 MongoDB 6 以上版本副本集及配置 SSL / TLS 协议
续上一篇 Linux 中使用 docker-compose 部署 MongoDB 6 以上版本副本集及配置 SSL / TLS 协议 前提:此篇文章是对上一篇文章的实战和项目中相关配置的使用,我这边针对 MongoDB 原有基础上做了增强,简化了 MongoDB 配置 SSL / TLS 协议上的支…...
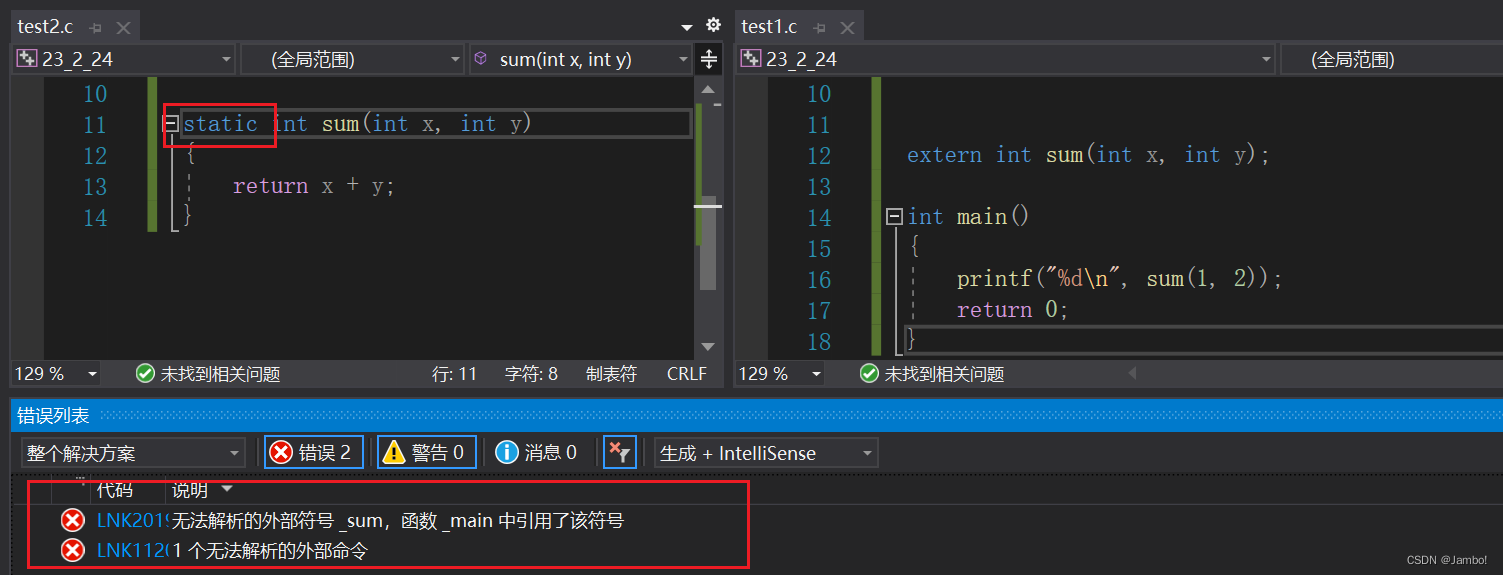
C语言static关键字
目录static修饰局部变量static修饰全局变量static修饰函数static是C语言的关键字,它有静态的意思static的三种用法:修饰局部变量修饰全局变量修饰函数 static修饰局部变量 我们先看一个程序: void print() {int a 0;a;printf("%d\n&…...

【华为OD机试模拟题】用 C++ 实现 - 单词接龙(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 货币单位换算(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 选座位(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 停车场最大距离(2023.Q1) 【华为OD机试模拟题】用 C++ 实现 - 重组字符串(2023.Q1) 【华为OD机试模…...
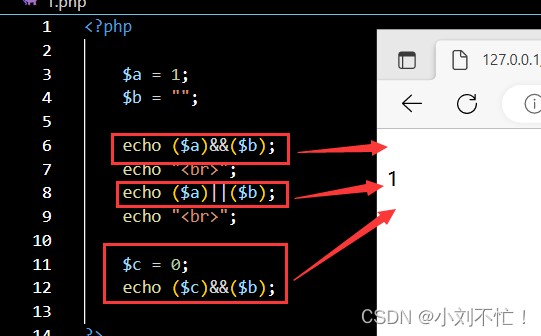
PHP基础(2)
PHP基础常用函数数组及多维数组数组遍历强制类型转换运算符赋值与基本运算字符串运算逻辑运算符常用函数 substr的用法是:substr(目标字符串,从字符串的哪个位置开始,然后返回往后的几个字符)strchr的用法是࿱…...
新特性)
Java8(JDK1.8)新特性
一、Java8(JDK1.8)新特性 1、Lamdba表达式 2、函数式接口 3、方法引用和构造引用 4、Stream API 5、接口中的默认方法和静态方法 6、新时间日期API 7、OPtional 8、其他特性 二、java8(JDK1.8)新特性简介 1、速度快; 2、代码少、简…...

【C语言】指针的定义和使用
指针一、什么是指针二、指针类型三、指针和数组的关系四、空指针五、野指针一、什么是指针 指针(Pointer)是编程语言中的一个对象,通过地址直接指向内存中该地址的值。由于通过地址能够找到所需的变量存储单元,可以说地址指向该变…...

Parameter ‘zpspid‘ not found
异常:nested exception is org.apache.ibatis.binding.BindingException: Parameter testypid not found. Available parameters are [ztpsXmjcxx, pageable, param1, param2]分析:以为是xml文件中没有对应的字段,一细看了几遍是有这个字段的…...
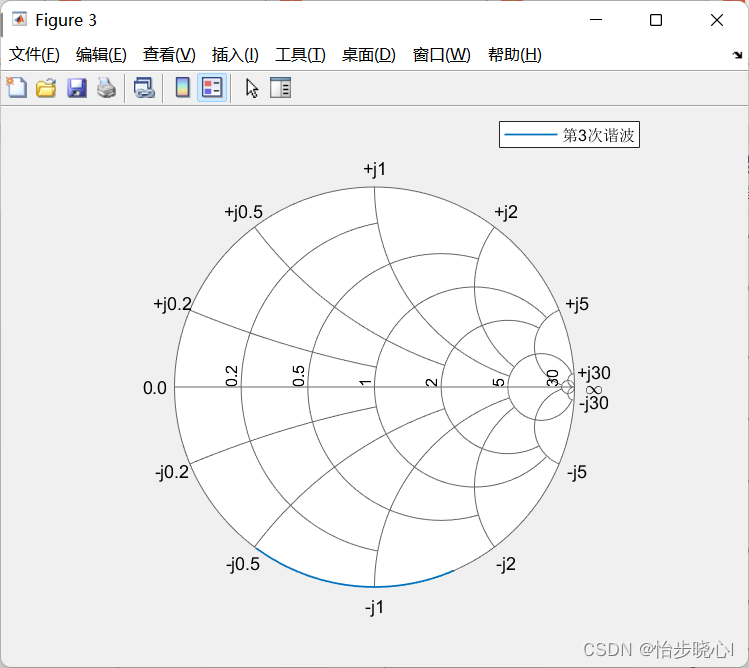
23、高自由度下的E类波形理论计算(附Matlab代码)
23、高自由度下的E类波形理论计算(附Matlab代码) 0、代码 任意占空比、电压导数条件下的E类波形与阻抗条件计算Matlab 注意修改路径,我这边是:!!!!!!&#…...
软件测试:用“bug”来表示“在电脑程序里的错误”
计算机基础知识计算机(personal computer)俗称电脑(pc),是现代一种用于高速计算的电子机器,可以进行数值计算,又可以进行逻辑判断,还具有存储记忆功能,且能够按照程序的运…...

Git命令
git init # 初始化本地git仓库(创建新仓库)git config --global user.name "xxx" # 配置用户名git config --global user.email "xxxxxx.com" # 配置邮件git config --global color.ui true # git status等命令自动着色git config -…...

Java的异常概念和类型
Java是一种流行的编程语言,拥有强大的异常处理机制,以帮助开发人员在程序出现异常时更好地处理错误情况。本文将介绍Java异常的概念和类型。异常的概念在Java中,异常是指在程序运行时发生的错误或异常情况。例如,当程序试图打开不…...

【Leedcode】环形链表必备的面试题和证明题(附图解)
环形链表必备的面试题和证明题(附图解) 文章目录环形链表必备的面试题和证明题(附图解)前言一、第一题1.题目2.思路3.代码4.延伸问题(1)证明题一:(2)证明题二:二、第二题1.题目2.思路延伸的证明题总结前言 …...

Vulnhub靶场----7、DC-7
文章目录一、环境搭建二、渗透流程三、思路总结一、环境搭建 DC-7下载地址:https://download.vulnhub.com/dc/DC-7.zip kali:192.168.144.148 DC-7:192.168.144.155 二、渗透流程 nmap -T5 -A -p- -sV -sT 192.168.144.155思路: …...
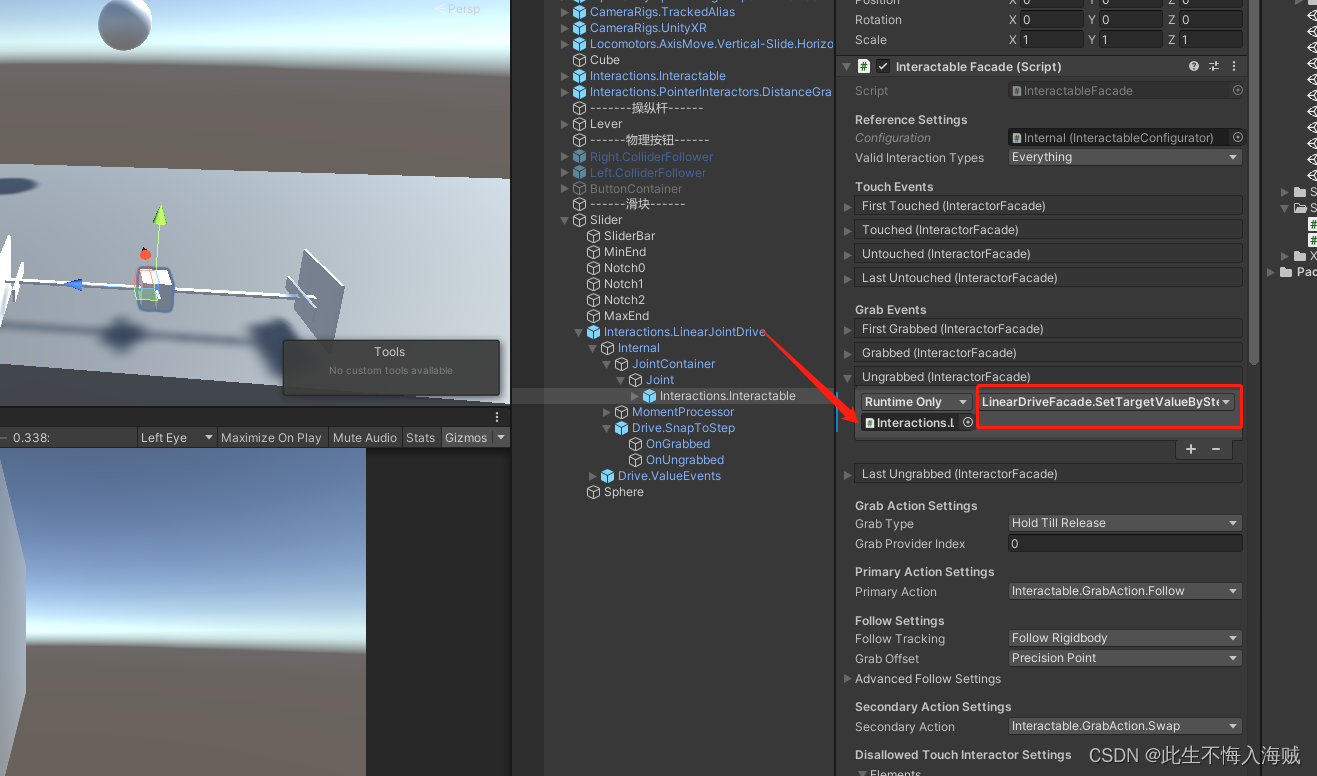
【Unity VR开发】结合VRTK4.0:创建滑块
语录: 只有经历地狱般的磨练,才能炼出创造天堂的力量。 前言: 滑块是一个非常简单的控件,它允许通过沿有限的驱动轴滑动 Interactable 来选择不同的值。我们将使用线性驱动器创建一个滑块控件,该控件允许我们根据与滑…...

Latex中的表格(2)
Latex中的表格一、一个加脚注的三线表的例子二、表格中加注释三、并排的表格3.1 使用小页环境并排表格3.2 使用子表格并排表格四、一个复杂的表格五、一个长表格这篇文章主要罗列一些特殊的表格例子。内容来自:一篇北师大学位论文模板,详见https://githu…...
输运定理)
(七)输运定理
本文主要内容包括:1. 物质积分2. 曲线上物质积分的时间变化率3. 曲面上物质积分的时间变化率4. 体积域上物质积分的时间变化率 (Reynolds 输运定理)1. 物质积分 考虑 t0t_0t0 时刻参考构型中由物质点 X⃗\vec{X}X所形成的 物质曲线 ct0c_{t_0}ct0、物质曲面 …...

ABBYYFineReader15免费电脑pdf文档文字识别软件
ABBYYFineReader是一款OCR文字识别软件,它可以对图片、文档等进行扫描识别,并将其转换为可编辑的格式,比如Word、Excel等,操作也是挺方便的。 我们在官网找到该软件并进行下载,打开软件后,选择转换为“Mic…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
