c++ 的 Eigen库写 AX=XB的矩阵求解代码
1.AX=XB的矩阵求解代码(3*3)
#include <iostream>
#include <Eigen/Dense>int main()
{// 定义矩阵A和BEigen::MatrixXd A(3, 3);A << 1, 2, 3,4, 5, 6,7, 8, 9;Eigen::MatrixXd B(3, 3);B << 10, 11, 12,13, 14, 15,16, 17, 18;// 求解AX=XBEigen::MatrixXd X = Eigen::MatrixXd::Zero(3, 3);Eigen::MatrixXd I = Eigen::MatrixXd::Identity(3, 3);Eigen::MatrixXd A_ = Eigen::kroneckerProduct(I, A);Eigen::MatrixXd B_ = Eigen::kroneckerProduct(B.transpose(), I);Eigen::MatrixXd AB = A_ - B_;Eigen::VectorXd b = Eigen::VectorXd::Zero(9);b(8) = 1;Eigen::VectorXd x = AB.colPivHouseholderQr().solve(b);X = Eigen::Map<Eigen::MatrixXd>(x.data(), 3, 3).transpose();// 输出结果std::cout << "A = \n" << A << std::endl;std::cout << "B = \n" << B << std::endl;std::cout << "X = \n" << X << std::endl;return 0;
}
这里我们使用了Eigen库的kroneckerProduct()函数实现Kronecker积,使用colPivHouseholderQr()函数进行矩阵求解,得到X的值。
2.可以使用C++ Eigen库来求解线性方程组Ax=xB,其中A和B是两个已知的4x4矩阵。下面是一个使用Eigen库求解线性方程组的示例代码:
#include <iostream>
#include <Eigen/Dense>int main()
{// 定义矩阵A和BEigen::Matrix4d A, B;// 设置A和B的值A << 1, 2, 3, 4,5, 6, 7, 8,9, 10, 11, 12,13, 14, 15, 16;B << 16, 15, 14, 13,12, 11, 10, 9,8, 7, 6, 5,4, 3, 2, 1;// 求解线性方程组Ax=xBEigen::Matrix4d X = A.lu().solve(B);// 输出解矩阵Xstd::cout << "The solution is:\n" << X << std::endl;return 0;
}
在上述代码中,我们首先定义了两个4x4的矩阵A和B,并设置了它们的值。然后,我们使用Eigen库中的lu()方法来求解线性方程组Ax=xB,并将结果保存在矩阵X中。最后,我们输出解矩阵X的值。在实际应用中,矩阵A和B的维数可能会很大,但使用Eigen库可以轻松地求解这样的线性方程组。
3.下面是使用C++的Eigen库解决AX=XB问题并找到最优解的代码。假设A和B都是4x4的矩阵,X是待求解的4x4矩阵。
#include <Eigen/Dense>using namespace Eigen;int main()
{Matrix4d A; // 定义4x4的矩阵AMatrix4d B; // 定义4x4的矩阵B// 填充A和B的值A << 1, 2, 3, 4,5, 6, 7, 8,9, 10, 11, 12,13, 14, 15, 16;B << 1, 2, 3, 4,5, 6, 7, 8,9, 10, 11, 12,13, 14, 15, 16;Matrix4d X; // 定义待求解的4x4矩阵X// 求解AX=XBEigen::GeneralizedSelfAdjointEigenSolver<Matrix4d> eig(A, B);// X = eig.eigenvectors().col(0);X = eig.eigenvectors();// 打印结果std::cout << "X = \n" << X << std::endl;return 0;
}
在上述代码中,我们使用Eigen的Matrix4d类定义矩阵A、B和X。在填充A和B的值后,我们使用GeneralizedSelfAdjointEigenSolver方法求解AX=XB,并将最优解存储在矩阵X的第一列中。最后,我们打印出矩阵X的值。
需要注意的是,GeneralizedSelfAdjointEigenSolver方法只能用于求解最优解,如果需要找到所有解,可以使用generalizedEigenSolver()方法。同时需要注意,由于AX=XB可能存在多个解,因此此代码仅返回其中一个最优解。
相关文章:

c++ 的 Eigen库写 AX=XB的矩阵求解代码
1.AXXB的矩阵求解代码(3*3) #include <iostream> #include <Eigen/Dense>int main() {// 定义矩阵A和BEigen::MatrixXd A(3, 3);A << 1, 2, 3,4, 5, 6,7, 8, 9;Eigen::MatrixXd B(3, 3);B << 10, 11, 12,13, 14, 15,16, 17, 18;// 求解AXXBEigen::Mat…...
正点原子linux驱动篇
linux驱动开发与裸机开发的区别 裸机直接操作寄存器,有些mcu提供了库,但还是很底层 1、linux驱动开发直接操作寄存器很麻烦不现实,主要是根据linux驱动框架进行开发(就是有很多操作都是一样的,我们只需要对一个程序模…...

MATLAB绘制雷达图/蜘蛛图
雷达图/蜘蛛图 1 方法一 函数来源为MATLAB | 如何使用MATLAB绘制雷达图(蜘蛛图) 1.1 调用函数 1.2 案例 2 方法二 函数来源为MATLAB帮助-spider_plot 2.1 调用函数 语法(Syntax): spider_plot(P)spider_plot(P, Name, Value, ...)h …...

算法入门,十字路口选择的案例,如果是南方,则向前行
从if判断start; 十字路口的案例 class HelloWorld { static void Main(string[] args) { /* Write C# code in this online editor and run it. */ Console.WriteLine("Hello World!"); string f…...
父传子与子传父步骤
父传子: 问题:父页面中引入子组件 把想要传给子页面的值用在子组件中用 :值“值” (用同一个值好区分)来绑定。 在子页面中用props接收 子组件不能改变父组件传过来的值。(传多个页面的时候是,比如父传孙的时候我会…...

Java concurrency - Task Execution
1.在单个线程里处理所有的请求:接受请求-处理请求 优点:逻辑简单 缺点:吞吐量低,资源利用率低,响应时间长 2.每个任务分配一个单独的线程来处理: 接受请求-创建线程-在线程里处理请求 优点: …...

浅谈BOM
什么是BOM BOM对于每个前端都不陌生,但是很多人都停留在表面,而没有深层次的研究过它。JavaScript有一个非常重要的运行环境就是浏览器,而且浏览器本身又作为一个应用程序需要对其本身进行操作,所以通常浏览器会有对应的对象模型…...

每日学术速递2.24
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.LG 1.BUAA_BIGSCity: Spatial-Temporal Graph Neural Network for Wind Power Forecasting in Baidu KDD CUP 2022 标题:BUAA_BIGSCity:百度KDD CUP 2022风电预测…...
)
SpringBoot 面试问答总结(VIP典藏版)
1. 什么是 Spring Boot? Spring Boot 是 Spring 开源组织下的子项目,是 Spring 组件一站式解决方案,主要是简化了使用Spring 的难度, 简省了繁重的配置,提供了各种启动器,使开发者能快速上手。 2. 为什…...

CSS 定位网页元素【快速掌握知识点】
目录 前言 一、position: static 二、position: relative 三、position: absolute 四、position: fixed 五、position: sticky 前言 当我们在设计网页时,经常需要对网页中的元素进行定位,以便它们出现在我们想要的位置。在 CSS 中,我们…...
)
构建Docker基础镜像(ubuntu20.04+python3.7.1+chrome101+chromedriver101)
文章目录 一、前置条件1.下载 chrome【google-chrome-stable_current_amd64.deb】2.下载 chromedriver【chromedriver_linux64.zip】3.创建 ubuntu 镜像源文件【sources.list】二、构建方法1.构建目录1.创建DockerFile2.打包镜像一、前置条件 要先下载一个支持 linux 的 浏览器…...
最新最全Java面试知识
工作也有好些年了,从刚毕业到前几年看过无数的面试题,在这个过程中也作为面试官面试过其他人,总想着自己写一个面试总结,随着自我认识的变化,一些知识点的理解也越来越不一样了。写下来温故而知新。很多问题可能别人也…...

个人电脑需求严重疲软,联想集团财务前景仍不乐观
来源:猛兽财经 作者:猛兽财经 财务业绩 联想集团(00992)于2月16日盘后公布了2023财年第三季度财报。 财报显示联想集团2023年第三季度的收入为152.67亿美元,从2022年第三季度的2011.27亿美元下降了24.1%。这也导致该公…...

软件测试面试在简历上写了“精通”后,拥有工作经验的我被面试官问到窒息...
前言 如果有真才实学,写个精通可以让面试官眼前一亮! 如果是瞎写?基本就要被狠狠地虐一把里! 最近在面试,我现在十分后悔在简历上写了“精通”二字… 先给大家看看我简历上的技能列表: 熟悉软件测试理…...

色环电容读数方法要点总结
🏡《总目录》 目录 1,概述2,读数方法3,颜色对照表3.1,颜色与电容值数字对照关系表3.2,颜色与10的指数数字对照关系表3.3,颜色与误差对照关系表4,总结1,概述 本文简单介绍色环电容的读数方法。 2,读数方法 如下图所示色环电容共有四个色环。最粗的被命名为第1环,依次…...
C++函数新思想和标准的输入和输出
欢迎来观看温柔了岁月.c的博客目前设有C学习专栏C语言项目专栏数据结构与算法专栏目前主要更新C学习专栏,C语言项目专栏不定时更新待C专栏完毕,会陆续更新C项目专栏和数据结构与算法专栏一周主要三更,星期三,星期五,星…...
)
华为OD机试真题Java实现【汽水瓶】真题+解题思路+代码(20222023)
汽水瓶 有这样一道智力题:“某商店规定:三个空汽水瓶可以换一瓶汽水。小张手上有十个空汽水瓶,她最多可以换多少瓶汽水喝?”答案是 5 瓶,方法如下:先用 9 个空瓶子换3瓶汽水,喝掉 3 瓶满的,喝完以后 4 个空瓶子,用 3 个再换一瓶,喝掉这瓶满的,这时候剩 2 个空瓶子。…...
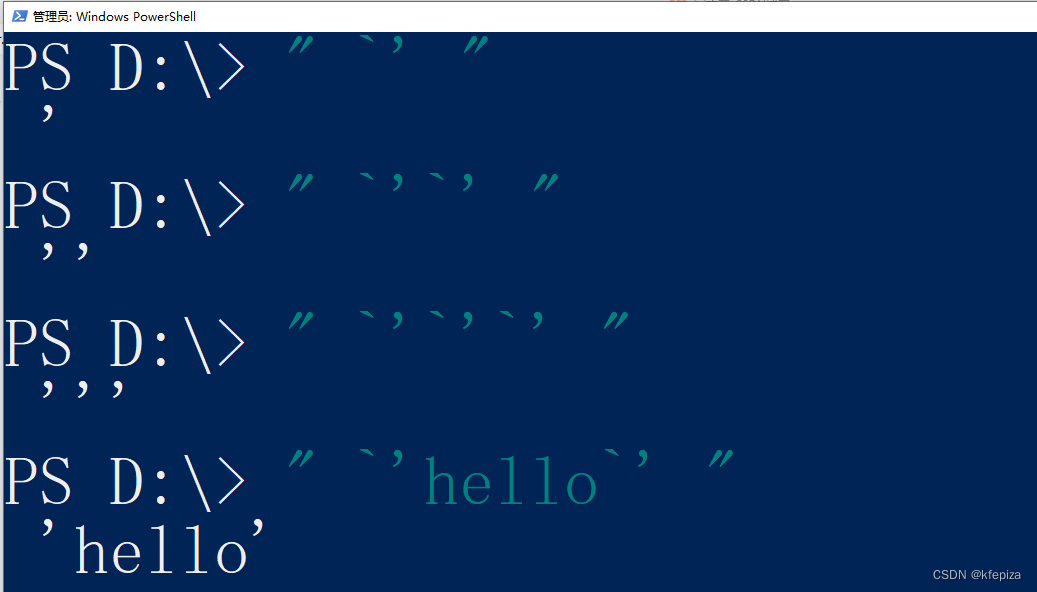
WindownsPowershell中的单引号和双引号
WindownsPowershell中的单引号和双引号 目录标题WindownsPowershell中的单引号和双引号单引号对中,可以直接写双引号双引号对中,可以直接写单引号反引号 可以在 双引号对中表示转义双引号对中, 可以用 反引号双引号 表示一个双引号双引号对中, 可以用 反引号单引号 表示一个单引…...

【华为OD机试模拟题】用 C++ 实现 - 数组组成的最小数字(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

Ae:使用代理
如果希望加快合成的预览或渲染速度,可考虑对素材使用代理 Proxy。虽然在 Ae 中,可以指定任何的静止图像或视频为代理,但一般情况下还是建议创建源素材的低分辨率版本来作为代理。对素材创建或指定代理后,可随意切换是否使用代理来…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
