力扣--第三大的数
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。
示例 1:
输入:[3, 2, 1] 输出:1 解释:第三大的数是 1 。
示例 2:
输入:[1, 2] 输出:2 解释:第三大的数不存在, 所以返回最大的数 2 。
示例 3:
输入:[2, 2, 3, 1] 输出:1 解释:注意,要求返回第三大的数,是指在所有不同数字中排第三大的数。 此例中存在两个值为 2 的数,它们都排第二。在所有不同数字中排第三大的数为 1 。
超啰嗦写法。。。。。。。。
class Solution {public int thirdMax(int[] nums) {Arrays.sort(nums);if(nums.length<3||(nums[nums.length-1]==nums[0]) return nums[nums.length-1];for(int i=nums.length-1;i>=0;i--){if(i-1<0) return nums[nums.length-1];if(nums[i]!=nums[i-1]){//说明nums[i-1]第二大int a=i-3;if(i-2<0) return nums[nums.length-1];if(nums[i-1]!=nums[i-2]){return nums[i-2];}else{if(a>=0){for(int j=a;j>=0;j--){if(nums[j]!=nums[i-1]){return nums[j];}}}else return nums[nums.length-1];}}}return nums[nums.length-1];}
}相关文章:

力扣--第三大的数
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。 示例 1: 输入:[3, 2, 1] 输出:1 解释:第三大的数是 1 。 示例 2: 输入:[1, 2] 输出࿱…...

Android 11.0 禁用adb reboot recovery命令实现正常重启功能
1.前言 在11.0的系统开发中,在定制recovery模块的时候,由于产品开发需要要求禁用recovery的相关功能,比如在通过adb命令的 adb reboot recovery的方式进入recovery也需要实现禁用,所以就需要了解相关进入recovery流程来禁用该功能 2.禁用adb reboot recovery命令实现正常…...

Cesium Vue(一)— 项目初始化配置
1. 创建VUE项目工程 创建项目 vue create cesium-vue配置Vue3 2. 创建vue.config.js文件 const { defineConfig } require(vue/cli-service)// The path to the CesiumJS source code const cesiumSource node_modules/cesium/Source; const cesiumWorkers ../Build/C…...
】)
【linux下centos7.9安装docker,docker-composed(root用户)】
一 安装docker 1.联网下载安装docker curl -fsSL https://get.docker.com | bash -s docker --mirror Aliyun 2.安装成功 docker -v 3.将docker注册为service,进入/etc/systemd/system/目录,并创建docker.service文件(注意insecure-registry修改成自己的…...
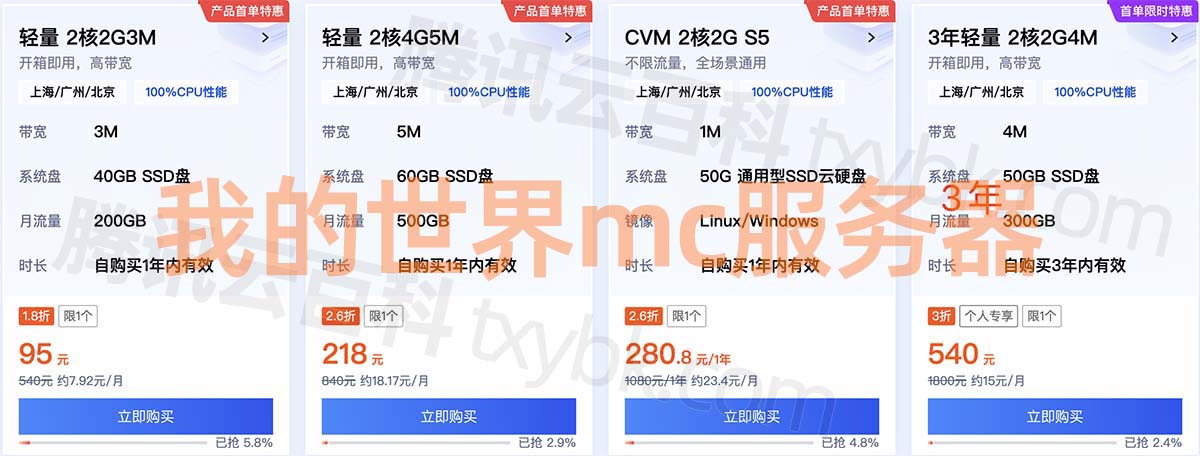
腾讯云我的世界mc服务器配置怎么选择?
使用腾讯云服务器开Minecraft我的世界服务器配置怎么选择?10人以内玩2核4G就够用了,开我的世界服务器选择轻量应用服务器就够了,腾讯云轻量CPU采用至强白金处理器,大型整合包一般1.12版本的,轻量2核4G配置都差不多的&a…...
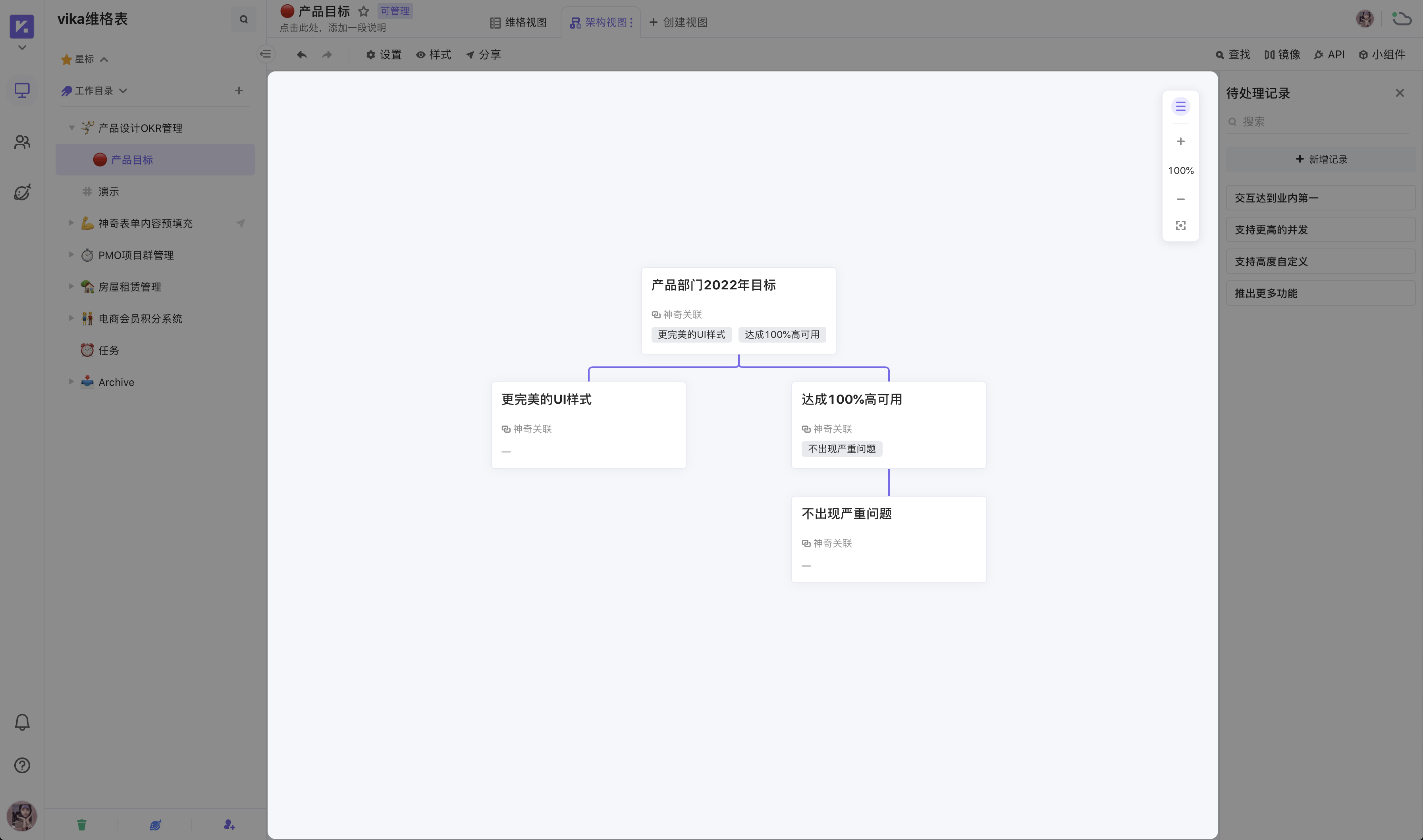
《低代码指南》——AI低代码维格云架构视图怎么用?
架构视图是一个展示信息层级关系的视图,轻轻拖拽卡片,就能搭建精巧缜密的企业组织架构视图、实现信息结构化。 利用好架构视图,可以很好地解决以下场景: 展示企业/团队的组织关系 可视化管理产品开发架构 统筹全员 OKR 完成情况 架构视图的基础知识 架构视图分为以下几个…...
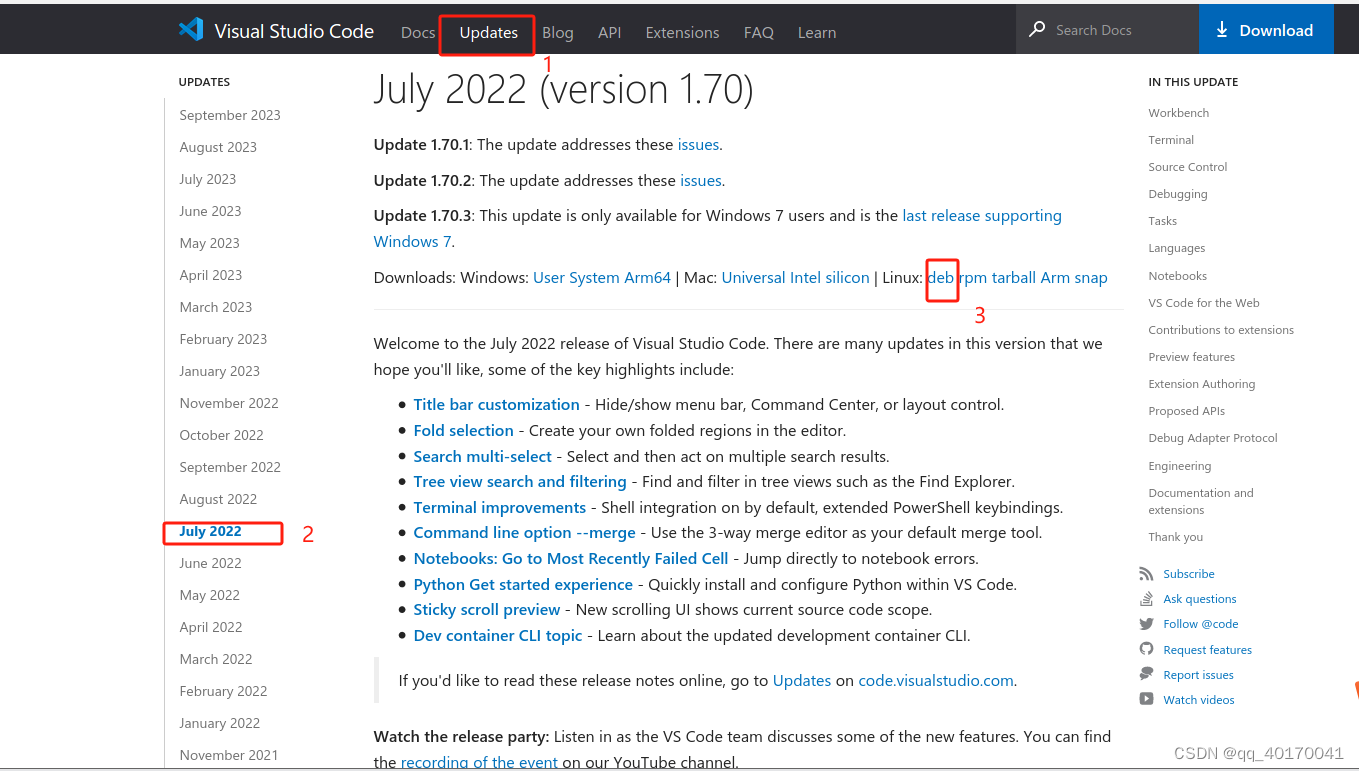
ubuntu16.04安装vscode遇到的code 依赖于 libnss3 (>= 2:3.30)解决
ubuntu16.04安装vscode遇到的code 依赖于 libnss3 (> 2:3.30);然而:系统中 libnss3:amd64 的版本为 2:3.28.4-0ubuntu0.16.04.14解决方法 一开始下载了最新版本的vscode,安装时出现了上面的错误状况,最新版本的依赖库版本过低的…...
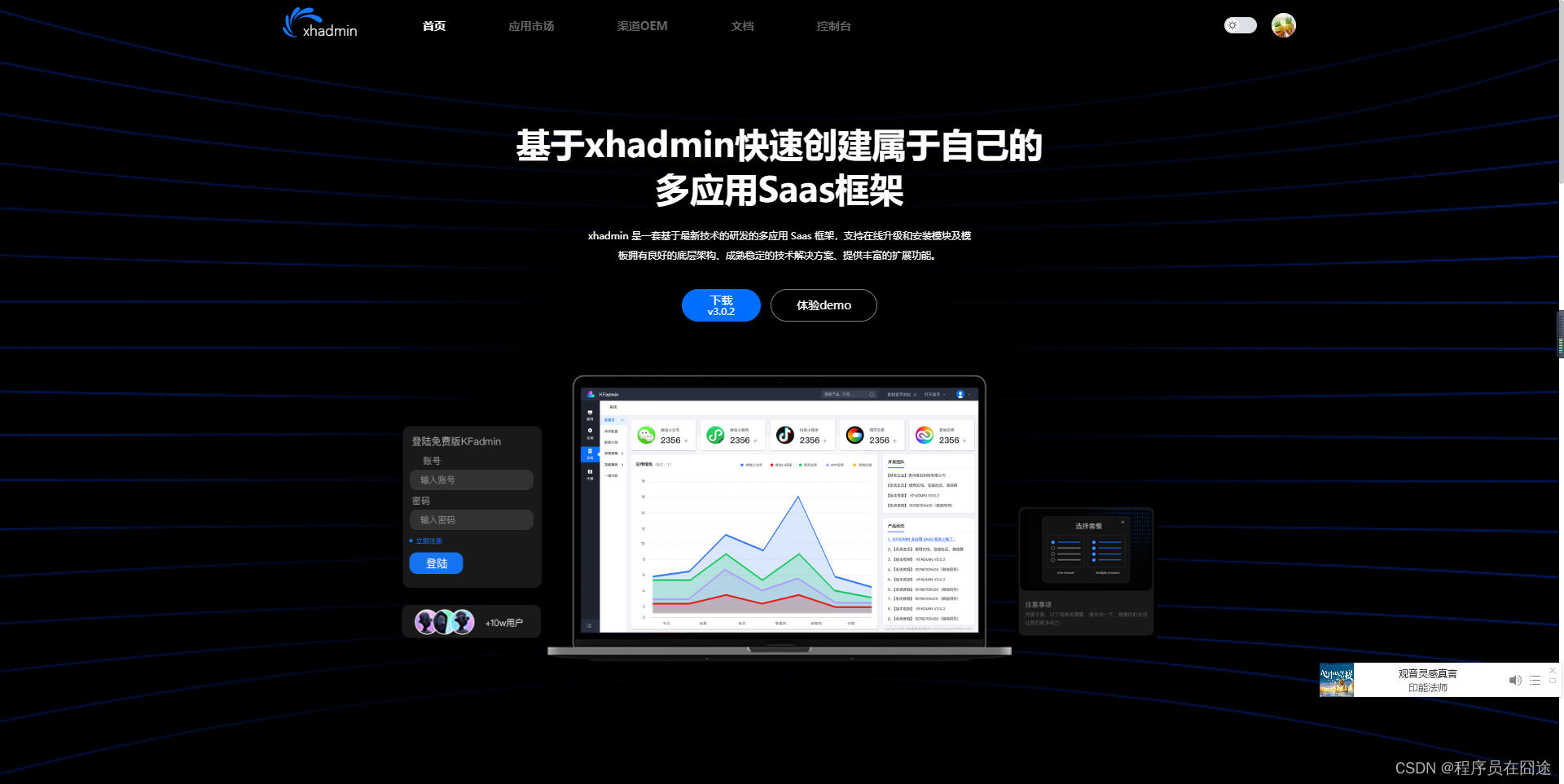
它来了,xhadmin多应用Saas框架正式发布!
这是一个很激动人心的时刻,因为这个框架从立项到现在已经一年多的时间了,先给大家欣赏下颜值吧。 上图所示是总后台的首页截图,看上去还是比较满意的,不过后续还有一些小小的调整。 应用市场的效果也是相当炸裂的,整体…...

PixMIM论文笔记
论文名称:PixMIM: Rethinking Pixel Reconstruction in Masked Image Modeling 发表时间:2023 年 3 月 4 日 作者及组织:上海人工智能实验室、西蒙菲莎大学、香港中文大学 GitHub:https://github.com/open-mmlab/mmselfsup/tree/d…...
设计师首选:最佳的5款网页设计软件
对于UI设计师来说,网页设计是一项必要的技能。如何做好网页设计?除了设计理念,网页设计和制作软件的应用也是不可或缺的。目前市场上有很多这样的软件,工人要想做好,就必须先磨利工具。如果他们想做网页设计࿰…...

ES6箭头函数
1.箭头函数的写法 如果函数内有返回值 var fn v > v 1 返回值如果不是表达式(是对象),用()括号返回 var fn v > ({ obj: v }) 返回值如果不是表达式(也不是对象)方法体内按正常写 var fu () > {var a 1;var b a1;return b; } 2.箭头函数和普通…...

毫米波雷达在环境监测中的关键作用
随着环境问题的日益凸显,精确、实时的环境监测成为了保护地球的关键一环。在这个背景下,毫米波雷达技术逐渐崭露头角,以其在环境监测中的独特优势成为不可或缺的工具。本文将探讨毫米波雷达在环境监测中的关键作用,以及它是如何应…...
print() 函数
二、print() 函数 这里先说一下 print() 函数,如果你是新手,可能对函数不太了解,没关系,在这里你只要了解它的组成部分和作用就可以了,后面函数这一块会详细说明的。 print() 函数由两部分构成 : 指令&a…...
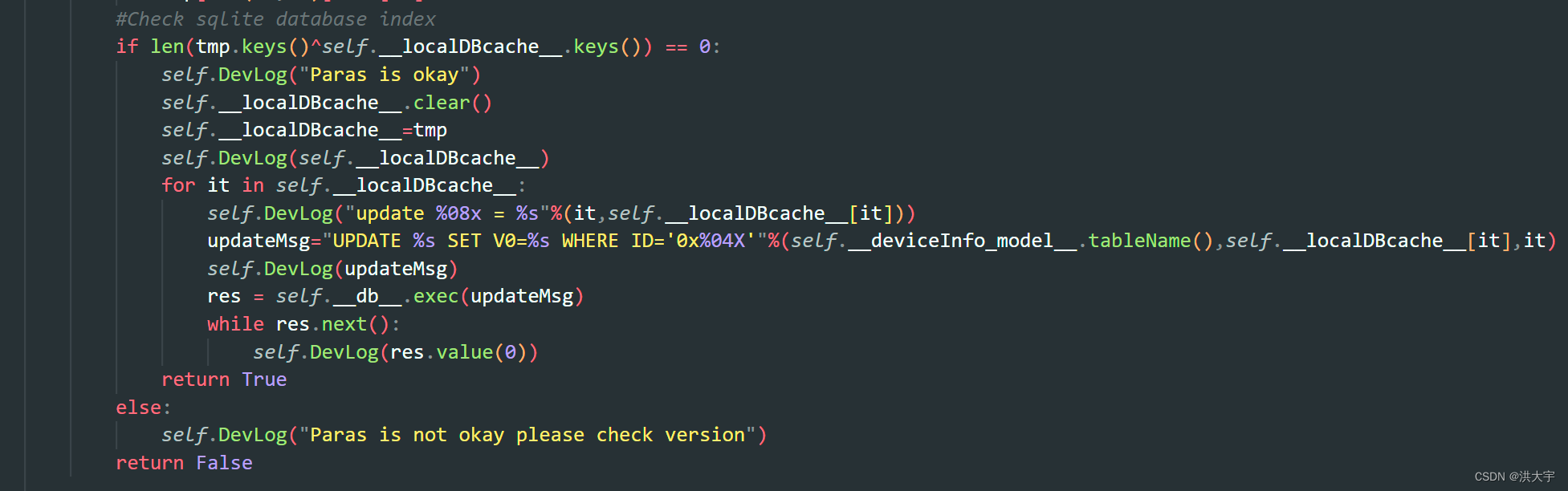
PyQt 小程序
设备管理程序 v0.0.1.0, 终于出了一个基础版本,… … 两个字典的键值判断 辛亏用的是Python 这个编码时间大大缩短了...

大模型技术实践(五)|支持千亿参数模型训练的分布式并行框架
在上一期的大模型技术实践中,我们介绍了增加式方法、选择式方法和重新参数化式方法三种主流的参数高效微调技术(PEFT)。微调模型可以让模型更适合于我们当前的下游任务,但当模型过大或数据集规模很大时,单个加速器&…...
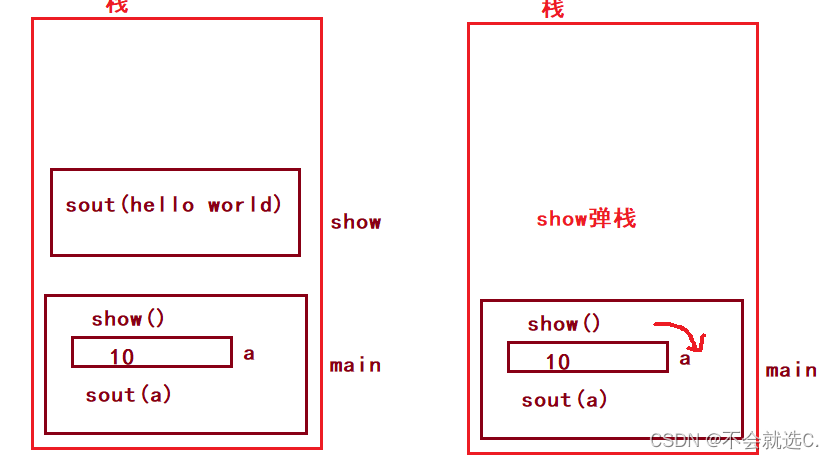
[正式学习java②]——数组的基本使用,java内存图与内存分配
一、数组的两种初始化方式 1.完整格式(静态初始化) 数据类型[] 数组名 new 数据类型[]{元素1,元素2…}; //范例 int[] arr new int[]{1,2,3,4}; 简化书写 一般我们会省略后面的 new 数据类型[] int[] arr {1,2,3,4}; 2.动态初始化 当不知道数组里面的初始值的时候…...

ESP32网络开发实例-TCP服务器数据传输
TCP服务器数据传输 文章目录 TCP服务器数据传输1、IP/TCP简单介绍2、软件准备3、硬件准备4、TCP服务器实现本文将详细介绍在Arduino开发环境中,实现一个ESP32 TCP服务器,从而达到与TCP客户端数据交换的目标。 1、IP/TCP简单介绍 Internet 协议(IP)是 Internet 的地址系统,…...

四川天蝶电子商务有限公司抖音电商服务引领行业标杆
随着电子商务的飞速发展,四川天蝶电子商务有限公司作为一家领先的抖音电商服务提供商,已经脱颖而出。本文将详细解析四川天蝶电子商务有限公司的抖音电商服务,让您一探究竟。 一、卓越的服务理念 四川天蝶电子商务有限公司始终坚持以客户为中…...

复制活动工作表和计数未保存工作簿进行
我给VBA下的定义:VBA是个人小型自动化处理的有效工具。可以大大提高自己的劳动效率,而且可以提高数据的准确性。我这里专注VBA,将我多年的经验汇集在VBA系列九套教程中。 作为我的学员要利用我的积木编程思想,积木编程最重要的是积木如何搭建…...

ORA-12541:TNS:no listener 无监听程序
问题截图 解决方法 1、删除Listener 新建一个新的 2、主机为服务器ip 3、设置数据库环境 只需要设置实例名不需要设置路径 4、服务命名 一样设置为ip 服务名与监听名一直 eg:orcl...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
