【C++ 中的友元函数:解密其神秘面纱】
友元函数,作为C++中一个重要但常常被误解的概念,经常让初学者感到困惑。本文将带您逐步了解友元函数的含义、用途以及如何正确使用它们。
什么是友元函数?
在C++中,友元函数是一种特殊的函数,它允许某个类或类的成员函数访问另一个类的私有成员。通常,C++中的封装性原则要求类的私有成员只能被该类的成员函数访问,但友元函数打破了这一规则。
为什么需要友元函数?
友元函数有其存在的合理用途。有些时候,我们可能需要让一个独立的函数能够访问某个类的私有数据。这种情况可能包括:
-
操作符重载:当我们需要重载一些操作符,例如
+、<<等,以便它们能够与自定义类一起使用时,友元函数非常有用。 -
提高性能:有时,友元函数可以直接访问类的私有成员,而不需要通过公共接口,从而提高代码的性能。
-
维护旧代码:在将已存在的C代码转化为C++时,友元函数可以用来维护现有的逻辑,而无需大规模重构。
如何定义友元函数?
在C++中,友元函数的定义和声明有一些特殊之处。以下是如何定义一个友元函数的步骤:
- 在要成为友元的类中声明友元函数,通常在类的声明中使用
friend关键字,如下所示:
class MyClass { public:// ...friend void FriendFunction(MyClass&); };
- 在类外部定义友元函数,允许它访问类的私有成员:
void FriendFunction(MyClass& obj) {// 在这里可以访问 MyClass 的私有成员 }
友元函数的限制和注意事项
尽管友元函数有其用途,但它们也有一些限制和注意事项:
-
滥用友元函数是不推荐的:过多地使用友元函数会破坏类的封装性,使代码更难维护。应该只在确实需要的情况下使用友元。
-
友元不具有继承性:友元关系不会继承到子类中。如果派生类需要访问基类的私有成员,需要单独声明友元关系。
-
友元函数可以是全局函数或其他类的成员函数:友元函数不一定要是全局函数,它们也可以是其他类的成员函数。
示例:操作符重载中的友元函数
一个常见的用例是在自定义类中使用友元函数来重载操作符。例如,让我们考虑一个表示复数的类 Complex,我们希望能够重载 + 操作符以便能够执行复数的加法。
class Complex {
private:double real;double imag;
public:Complex(double r, double i) : real(r), imag(i) {}// ...friend Complex operator+(const Complex& lhs, const Complex& rhs);
};Complex operator+(const Complex& lhs, const Complex& rhs) {return Complex(lhs.real + rhs.real, lhs.imag + rhs.imag);
}
在这个示例中,operator+ 函数是一个友元函数,它可以访问 Complex 类的私有成员。
结论
友元函数是C++中的一个强大但需要谨慎使用的特性。通过使用友元函数,您可以让独立的函数访问类的私有成员,从而实现更灵活的编程。然而,滥用友元函数可能会破坏类的封装性,因此需要谨慎使用。了解何时使用友元函数以及如何正确定义它们对于C++编程非常重要。希望本文有助于解开友元函数的神秘面纱,使您能够更好地利用这一特性。
相关文章:

【C++ 中的友元函数:解密其神秘面纱】
友元函数,作为C中一个重要但常常被误解的概念,经常让初学者感到困惑。本文将带您逐步了解友元函数的含义、用途以及如何正确使用它们。 什么是友元函数? 在C中,友元函数是一种特殊的函数,它允许某个类或类的成员函数…...
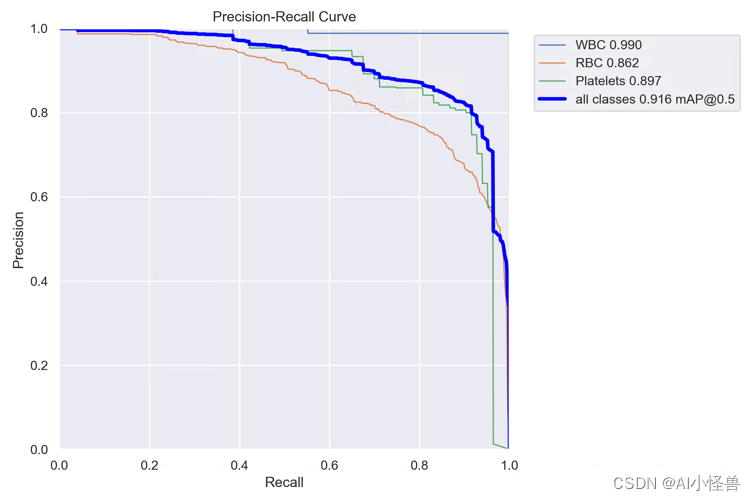
YOLOv8涨点技巧:手把手教程,注意力机制如何在不同数据集上实现涨点的工作,内涵多种网络改进方法
💡💡💡本文独家改进:手把手教程,解决注意力机制引入到YOLOv8在自己数据集不涨点的问题点,本文提供五种改进方法来解决此问题; ContextAggregation | 亲测在血细胞检测项目中涨点,…...

牛客:FZ12 牛牛的顺时针遍历
FZ12 牛牛的顺时针遍历 文章目录 FZ12 牛牛的顺时针遍历题目描述题解思路题解代码 题目描述 题解思路 通过一个变量来记录当前方向,遍历矩阵,每次遍历一条边,将该边的信息加入到结果中 题解代码 func spiralOrder(matrix [][]int) []int {…...
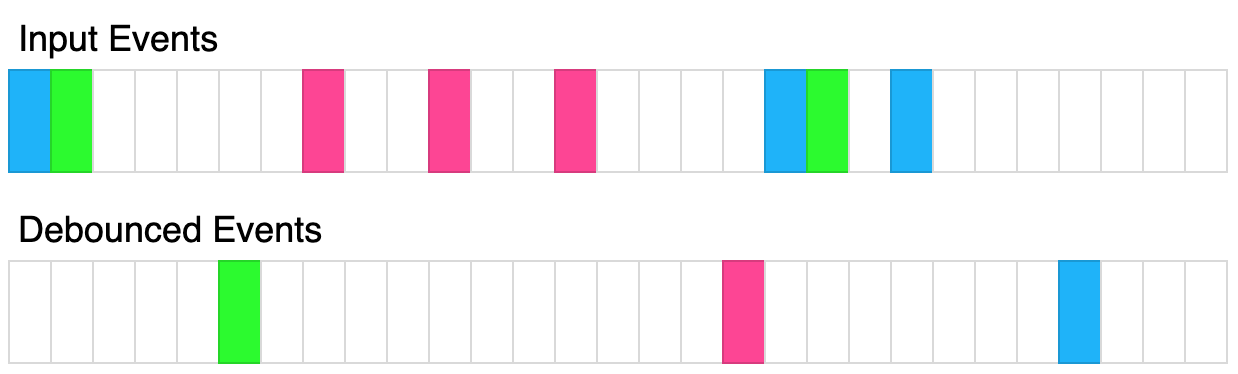
函数防抖(javaScript)
防抖说明 (1)防抖的目的: 当多次执行某一个动作的时候,限制函数调用的次数,节约资源。 (2)防抖的概念: 函数防抖(debounce):就是指触发事件后&…...
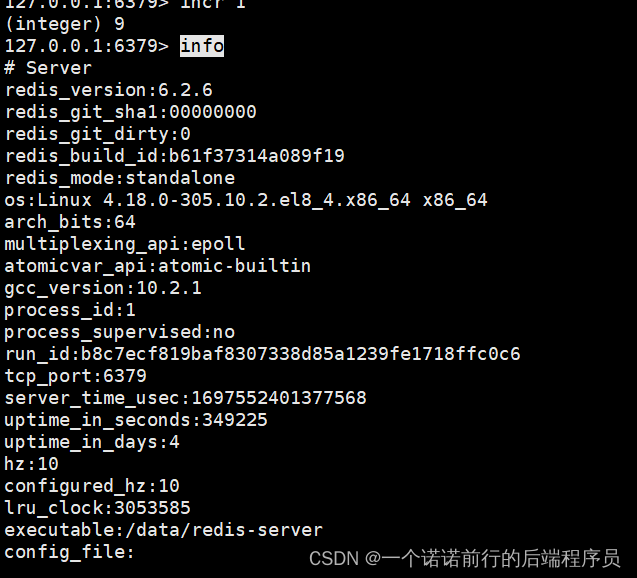
日常学习记录随笔-redis实战
redis的持久化(rdb,aof,混合持久化) redis的主从架构以及redis的哨兵架构 redis的clusterredis 是要做持久化的,一般用redis会把数据放到缓存中为了提升系统的性能 如果redis没有持久化,重启的化数据就会丢失,所有的请…...
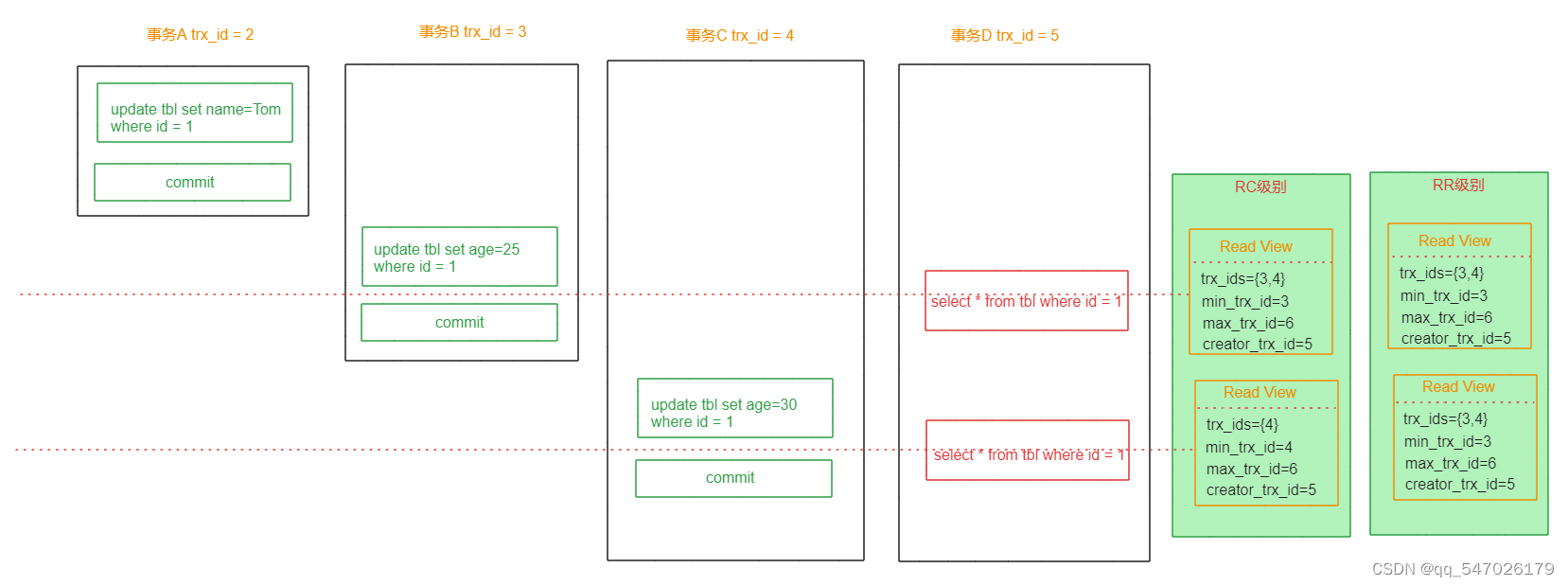
MySQL事务MVCC详解
一、概述 MVCC (MultiVersion Concurrency Control) 叫做多版本并发控制机制。主要是通过数据多版本来实现读-写分离,做到即使有读写冲突时,也能做到不加锁,非阻塞并发读,从而提高数据库并发性能。 MVCC只在已提交读(…...

SQL RDBMS 概念
SQL RDBMS 概念 RDBMS是关系数据库管理系统(Relational Database Management System)的缩写。 RDBMS是SQL的基础,也是所有现代数据库系统(如MS SQL Server、IBMDB2、Oracle、MySQL和MicrosoftAccess)的基础。 关系数据库管理系统(Relational Database Management Sy…...
onlyoffice的介绍搭建、集成过程。Windows、Linux
文章目录 什么是onlyoffice功能系统要求安装必备组件 windows搭建资源下载安装数据库onlyoffice安装测试 Linux搭建dockerdocker-compose 项目中用到的技术,做个笔记哈~ 什么是onlyoffice 在本地服务器上安装ONLYOFFICE Docs Community Edition Community Edition…...

37. 解数独
编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) 数独部分空…...
git cherry-pick 合并某次提交
一、无冲突的情况 1、合并其它分支某次提交 切换到主分支,想把其他分支的某次commit修改 合并到主分支上, 可以用 git cherry-pick 命令 比如,其它分支,某次提交的commit Hash 是30e48158badc39801f1ce3cb375a07b872d6f220 &a…...

【面试HOT100】子串普通数组矩阵
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于LeetCodeHot100进行的,每个知识点的修正和深入主要参考…...
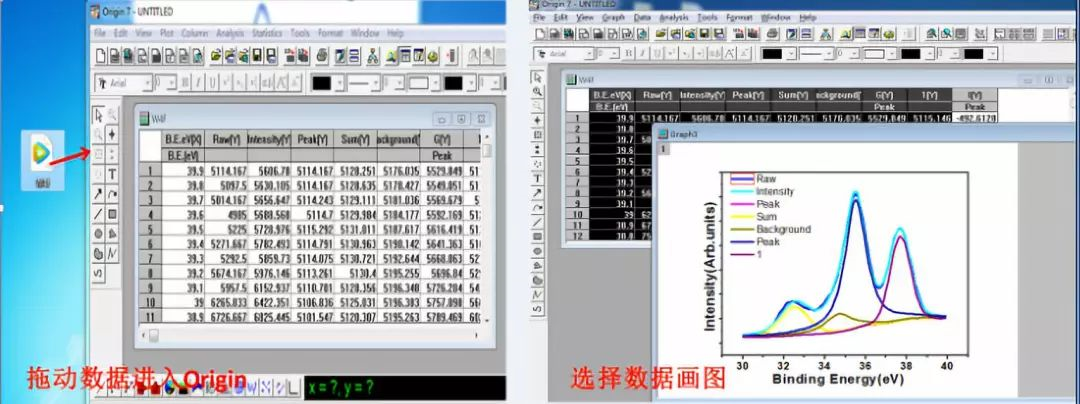
XPSpeak软件教程-科学指南针
在做X 射线光电子能谱(XPS)测试时,科学指南针检测平台工作人员在与很多同学沟通中了解到,好多同学仅仅是通过文献或者师兄师姐的推荐对XPS测试有了解,但是对于其软件操作还属于小白阶段,针对此,科学指南针检测平台团队…...

NLP算法面经 | 腾讯 VS 美团
作者 | 曾同学 编辑 | NewBeeNLP 面试锦囊之面经分享系列,持续更新中 后台回复『面试』加入讨论组交流噢 lz从3月初脚因打球扭伤了开始,投递简历,接二连三的面试鞭尸又面试,昨天才终于上岸了,分享经验~ 腾讯PCG看点&…...

【广州华锐互动】塔吊多人安拆VR互动培训系统
塔吊多人安拆VR互动培训系统由广州华锐互动制作,是一种基于VR技术的模拟实训系统,专门用于培训塔吊驾驶员和操作员。 在现实生活中,塔吊操作具有一定的危险性,尤其是在培训过程中容易发生意外。而使用VR互动实训系统,学…...
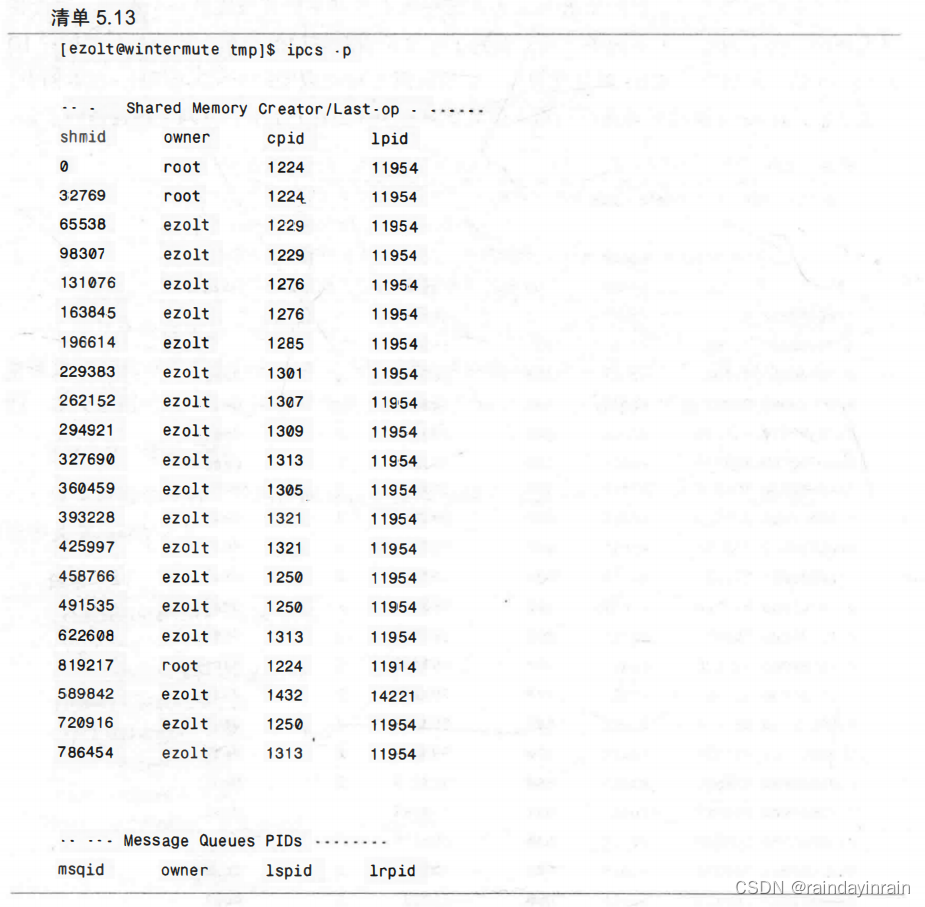
Linux性能优化--性能工具:特定进程内存
5.0 概述 本章介绍的工具使你能诊断应用程序与内存子系统之间的交互,该子系统由Linux内核和CPU管理。由于内存子系统的不同层次在性能上有数量级的差异,因此,修复应用程序使其有效地使用内存子系统会对程序性能产生巨大的影响。 阅读本章后&…...
MyLife - Docker安装rabbitmq
Docker安装rabbitmq 个人觉得像rabbitmq之类的基础设施在线上环境直接物理机安装使用可能会好些。但是在开发测试环境用docker容器还是比较方便的。这里学习下docker安装rabbitmq使用。 1. rabbitmq 镜像库地址 rabbitmq 镜像库地址:https://hub.docker.com/_/rabbi…...
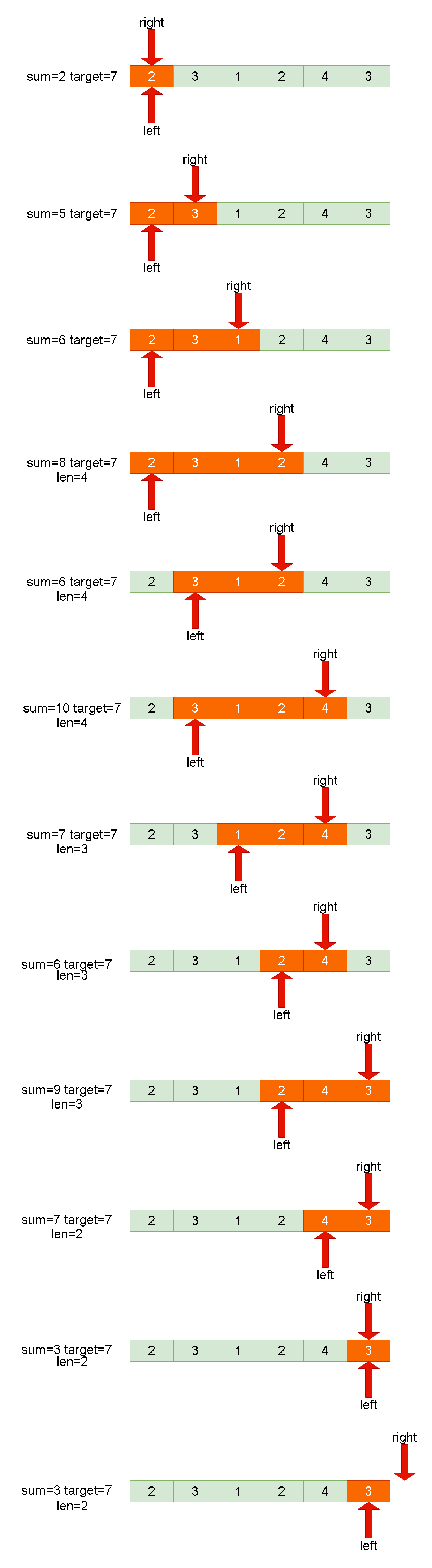
Leetcode刷题详解——长度最小的子数组
1. 题目链接:209. 长度最小的子数组 2. 题目描述: 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度**。**如果不…...

客流人数管理新趋势:景区客流采集分析系统的功能特点
随着旅游业的蓬勃发展,越来越多的人选择前往景区进行休闲和旅游。然而,人流量的增加也给景区管理带来了一系列的挑战。为了更好地管理和运营景区,景区客流采集分析系统应运而生。 一、案例展示 二、产品卖点 该系统利用先进的人工智能算法和…...

【仙逆】王林极限跑酷,藤厉自食恶果,仙逆战斗获好评,张虎命运被改写
Hello,小伙伴们,我是小郑继续为大家深度解析国漫资讯。 最新一集《仙逆》已经更新,相信很多小伙伴都已经先睹为快,在击杀了白展之后,张虎和王林担心其师傅即墨老人报复,因此躲到看似安全的藤家城,以为那里有…...

想要精通算法和SQL的成长之路 - 前缀和的应用
想要精通算法和SQL的成长之路 - 前缀和的应用 前言一. 区域和检索 - 数组不可变二. 二维区域和检索 - 矩阵不可变2.1 前缀和的计算2.2 用前缀和计算二维区域和 三. 矩形区域不超过 K 的最大数值和 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 区域和检索 - 数组不可变 原…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
