37. 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
示例 1:

输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] 输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] 解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个
class Solution {
public:bool isvaild(int row,int col,char val,vector<vector<char>>& board){//rowfor(int i = 0;i < 9;i++){if(board[row][i] == val) return false;}//colfor(int j = 0;j < 9;j++){if(board[j][col] == val) return false;}//九宫格int startx = (row/3)*3; // 假如在第一个九宫格,row/3=0,再*3=0;int starty = (col/3)*3; //假如在第二个九宫格,row/3=1,再*3=3; 我直呼nbfor(int i = startx;i < startx+3;i++){for(int j = starty;j < starty+3;j++){if(board[i][j] == val) return false;}}return true;}bool backtracking(vector<vector<char>>& board){for(int i = 0;i < board.size();i++){for(int j = 0;j < board[0].size();j++){//遇到空格if(board[i][j] == '.'){for(char a = '1';a <= '9';a++){//判断这里应该填入啥数字合法if(isvaild(i,j,a,board)){board[i][j] = a;//得将这个状态一直返回if(backtracking(board) == true) return true;board[i][j] = '.'; // 回溯}}return false; //填入0-9都不对,都不合法,填错了。}}}return true; //填完且填正确了。}void solveSudoku(vector<vector<char>>& board) {backtracking(board);}
};相关文章:

37. 解数独
编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) 数独部分空…...
git cherry-pick 合并某次提交
一、无冲突的情况 1、合并其它分支某次提交 切换到主分支,想把其他分支的某次commit修改 合并到主分支上, 可以用 git cherry-pick 命令 比如,其它分支,某次提交的commit Hash 是30e48158badc39801f1ce3cb375a07b872d6f220 &a…...

【面试HOT100】子串普通数组矩阵
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于LeetCodeHot100进行的,每个知识点的修正和深入主要参考…...
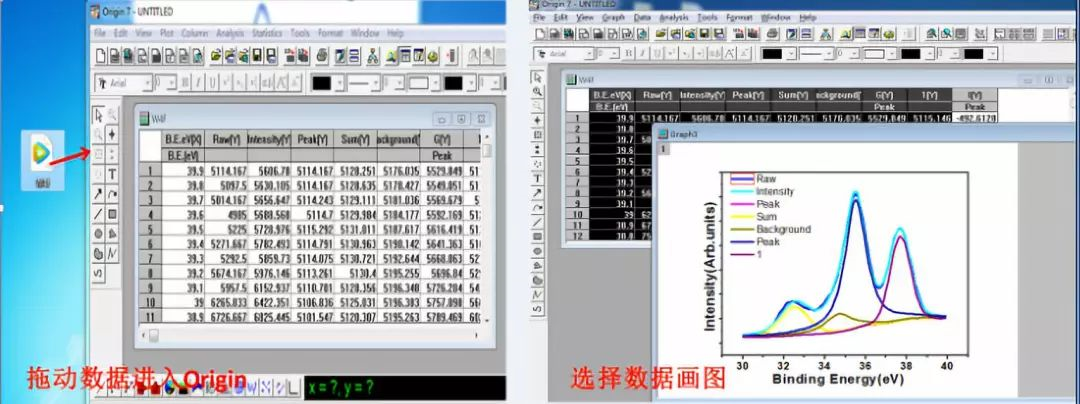
XPSpeak软件教程-科学指南针
在做X 射线光电子能谱(XPS)测试时,科学指南针检测平台工作人员在与很多同学沟通中了解到,好多同学仅仅是通过文献或者师兄师姐的推荐对XPS测试有了解,但是对于其软件操作还属于小白阶段,针对此,科学指南针检测平台团队…...

NLP算法面经 | 腾讯 VS 美团
作者 | 曾同学 编辑 | NewBeeNLP 面试锦囊之面经分享系列,持续更新中 后台回复『面试』加入讨论组交流噢 lz从3月初脚因打球扭伤了开始,投递简历,接二连三的面试鞭尸又面试,昨天才终于上岸了,分享经验~ 腾讯PCG看点&…...

【广州华锐互动】塔吊多人安拆VR互动培训系统
塔吊多人安拆VR互动培训系统由广州华锐互动制作,是一种基于VR技术的模拟实训系统,专门用于培训塔吊驾驶员和操作员。 在现实生活中,塔吊操作具有一定的危险性,尤其是在培训过程中容易发生意外。而使用VR互动实训系统,学…...
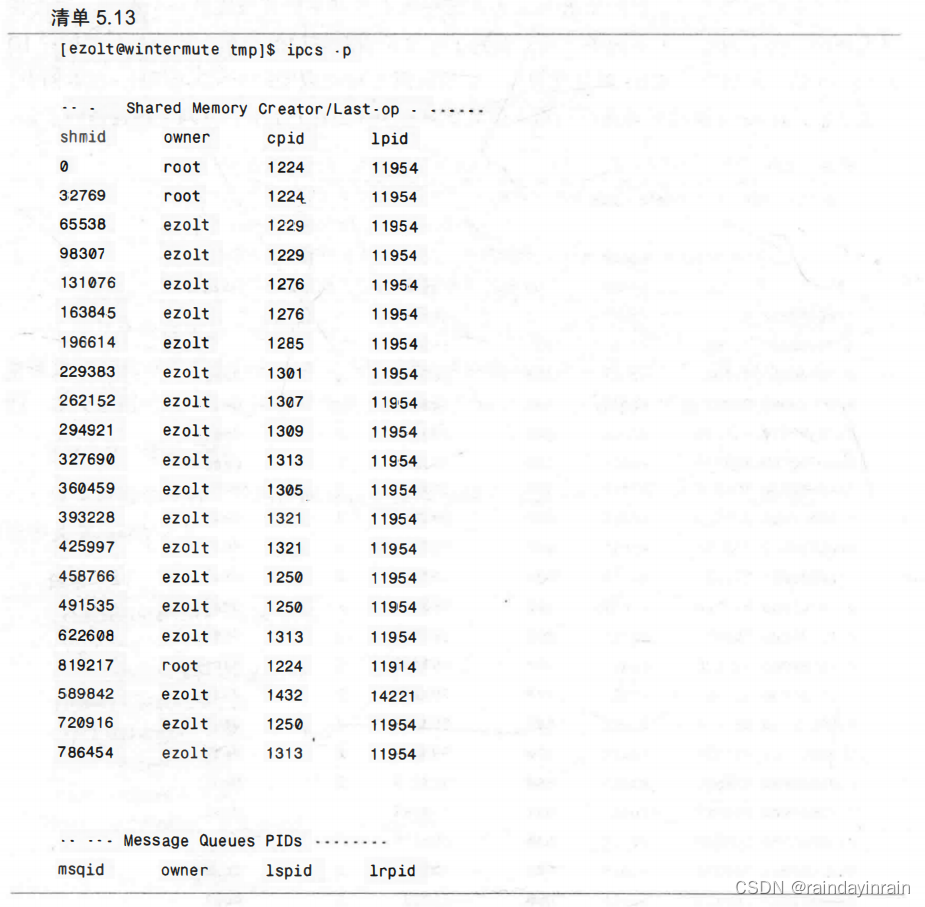
Linux性能优化--性能工具:特定进程内存
5.0 概述 本章介绍的工具使你能诊断应用程序与内存子系统之间的交互,该子系统由Linux内核和CPU管理。由于内存子系统的不同层次在性能上有数量级的差异,因此,修复应用程序使其有效地使用内存子系统会对程序性能产生巨大的影响。 阅读本章后&…...
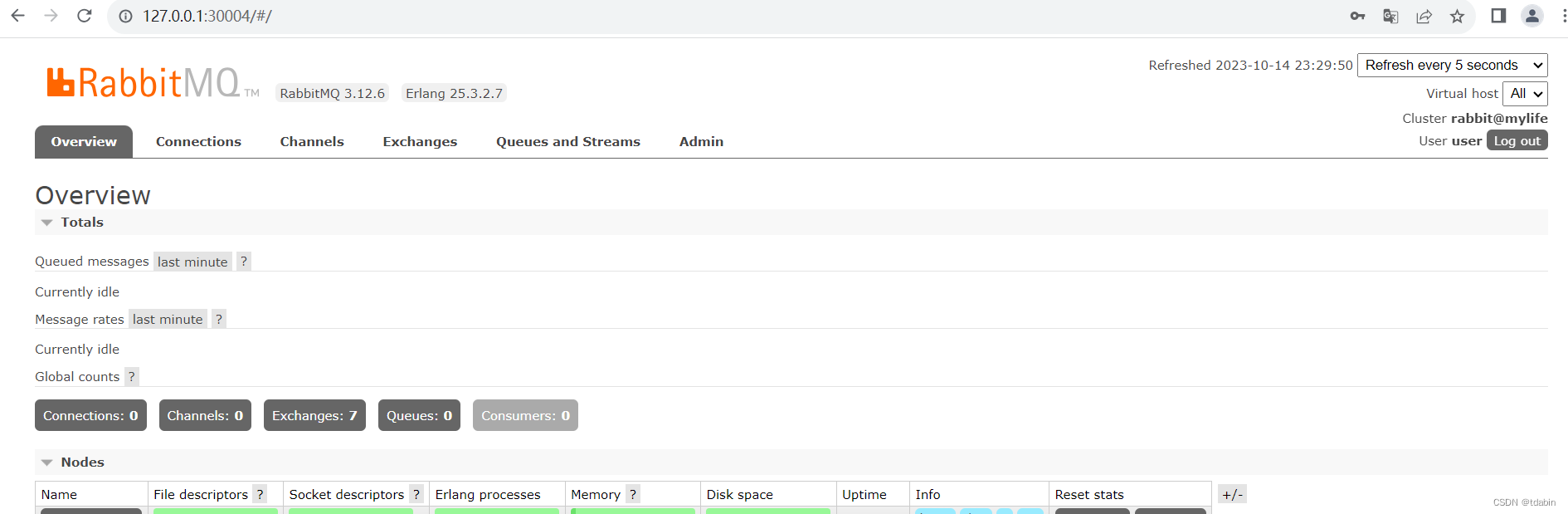
MyLife - Docker安装rabbitmq
Docker安装rabbitmq 个人觉得像rabbitmq之类的基础设施在线上环境直接物理机安装使用可能会好些。但是在开发测试环境用docker容器还是比较方便的。这里学习下docker安装rabbitmq使用。 1. rabbitmq 镜像库地址 rabbitmq 镜像库地址:https://hub.docker.com/_/rabbi…...
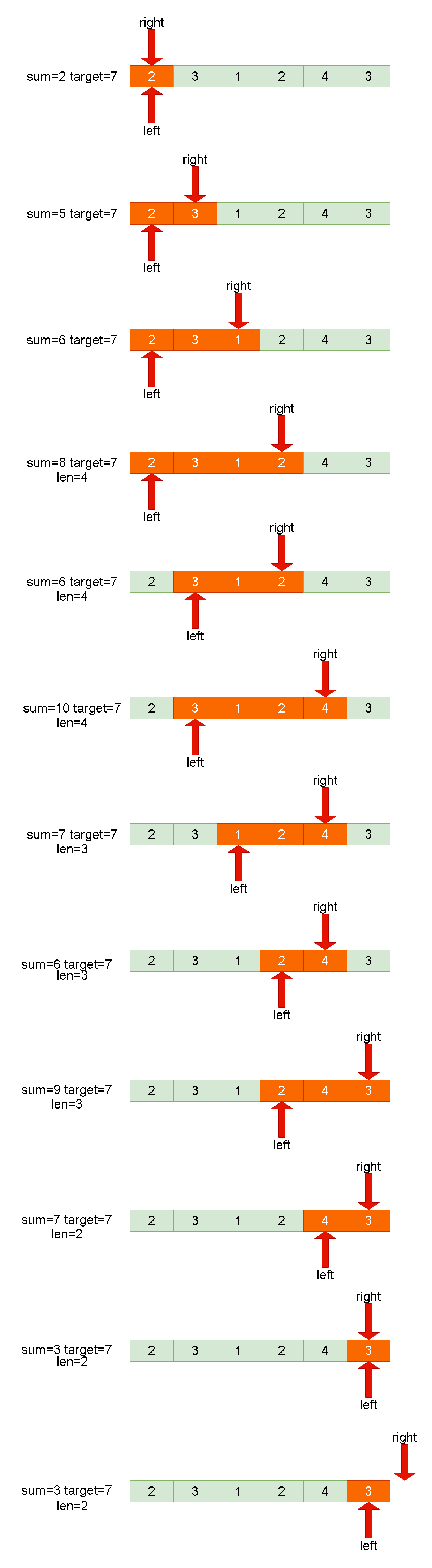
Leetcode刷题详解——长度最小的子数组
1. 题目链接:209. 长度最小的子数组 2. 题目描述: 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度**。**如果不…...

客流人数管理新趋势:景区客流采集分析系统的功能特点
随着旅游业的蓬勃发展,越来越多的人选择前往景区进行休闲和旅游。然而,人流量的增加也给景区管理带来了一系列的挑战。为了更好地管理和运营景区,景区客流采集分析系统应运而生。 一、案例展示 二、产品卖点 该系统利用先进的人工智能算法和…...

【仙逆】王林极限跑酷,藤厉自食恶果,仙逆战斗获好评,张虎命运被改写
Hello,小伙伴们,我是小郑继续为大家深度解析国漫资讯。 最新一集《仙逆》已经更新,相信很多小伙伴都已经先睹为快,在击杀了白展之后,张虎和王林担心其师傅即墨老人报复,因此躲到看似安全的藤家城,以为那里有…...

想要精通算法和SQL的成长之路 - 前缀和的应用
想要精通算法和SQL的成长之路 - 前缀和的应用 前言一. 区域和检索 - 数组不可变二. 二维区域和检索 - 矩阵不可变2.1 前缀和的计算2.2 用前缀和计算二维区域和 三. 矩形区域不超过 K 的最大数值和 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 区域和检索 - 数组不可变 原…...
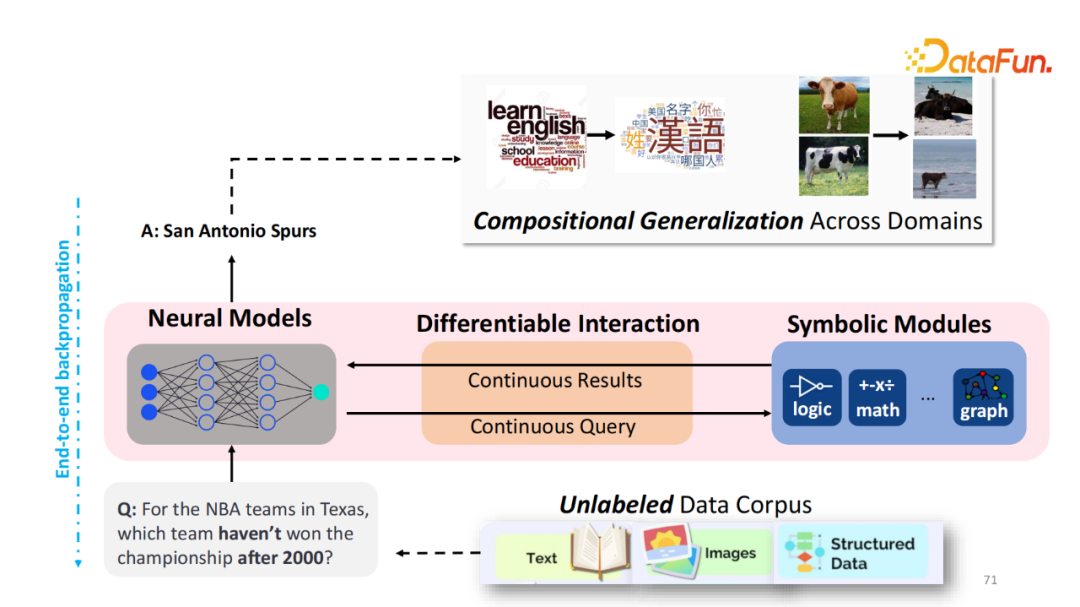
如何让大模型自由使用外部知识与工具
本文将分享为什么以及如何使用外部的知识和工具来增强视觉或者语言模型。 全文目录: 1. 背景介绍 OREO-LM: 用知识图谱推理来增强语言模型 REVEAL: 用多个知识库检索来预训练视觉语言模型 AVIS: 让大模型用动态树决策来调用工具 技术交流群 建了技术交流群&a…...

关注用户信息卡片
效果展示 CSS 知识点 box-shadow 属性回顾CSS 变量回顾 实现页面整体布局 <div class"card"><div class"box"><!-- 视频 --><div class"vide_box"><video src"user.mp4" type"video/mp4" aut…...

【Java基础面试十八】、说一说重写与重载的区别
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:说一说重写与重载的区别…...
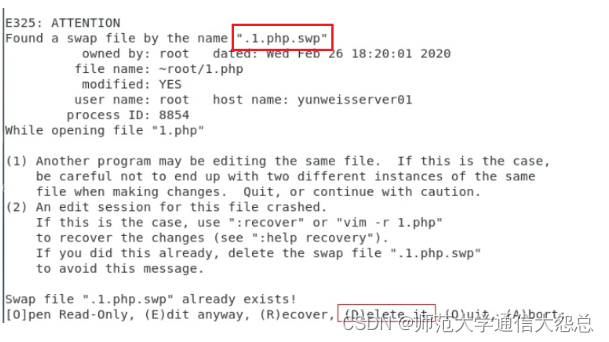
Linux文件管理(上)
一、VIM编辑器 1、vi概述 vi(visual editor)编辑器通常被简称为vi,它是Linux和Unix系统上最基本的文本编辑器,类似于Windows 系统下的notepad(记事本)编辑器。 2、vim编辑器 Vim(Vi improved)是vi编辑器…...
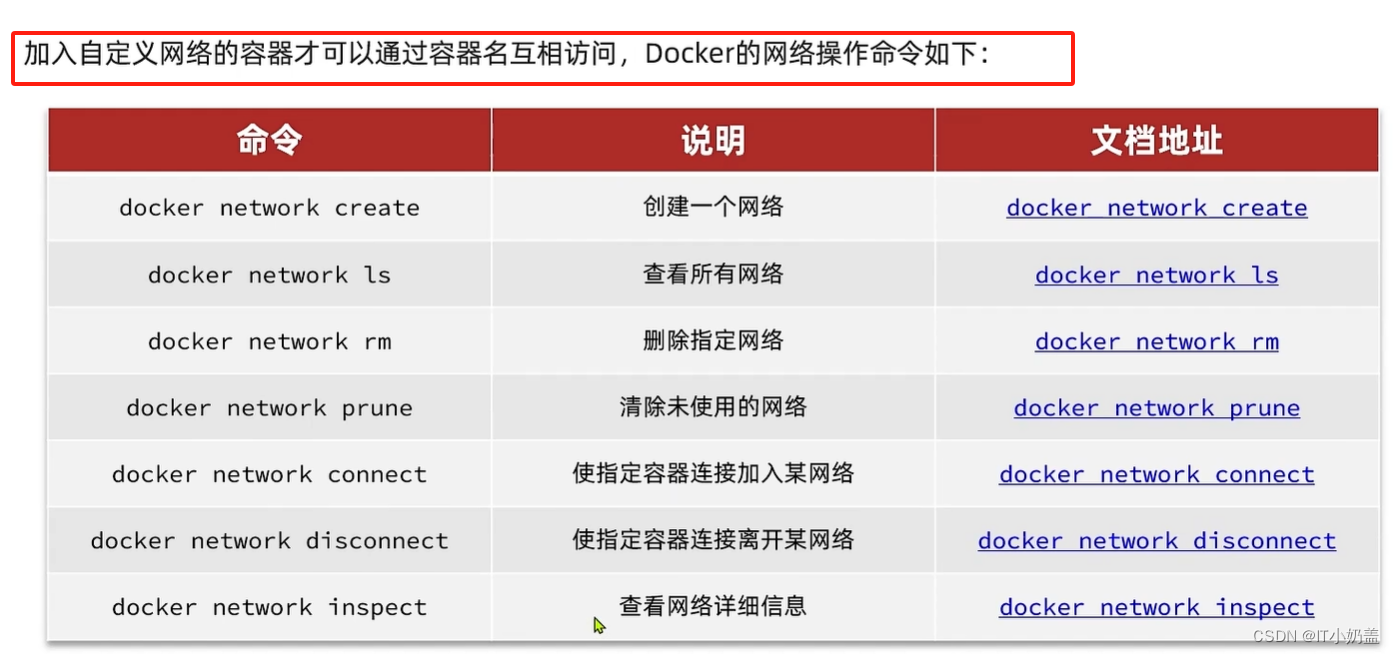
docker 复习
文章目录 1. docker 基础1.1 docker 安装配置镜像加速器拉取镜像的仓库: docker 部署Mysql 镜像docker 命令的详细解释docker 常见命令docker 数据卷docker 相关命令总结 2.自定义镜像2.1 dockerfile2.2 try 构建一个Java镜像,并部署2.3 总结: 3. docker…...

React之事件机制与事件绑定
一,时间机制 是什么 React基于浏览器的事件机制自身实现了一套事件机制,包括事件注册、事件的合成、事件冒泡、事件派发等 在React中这套事件机制被称之为合成事件 合成事件(SyntheticEvent) 合成事件是 React模拟原生 DOM事…...
spark stream入门案例:netcat准实时处理wordCount(scala 编程)
目录 案例需求 代码 结果 解析 案例需求: 使用netcat工具向9999端口不断的发送数据,通过SparkStreaming读取端口数据并统计不同单词出现的次数 -- 1. Spark从socket中获取数据:一行一行的获取 -- 2. Driver程序执行时,…...
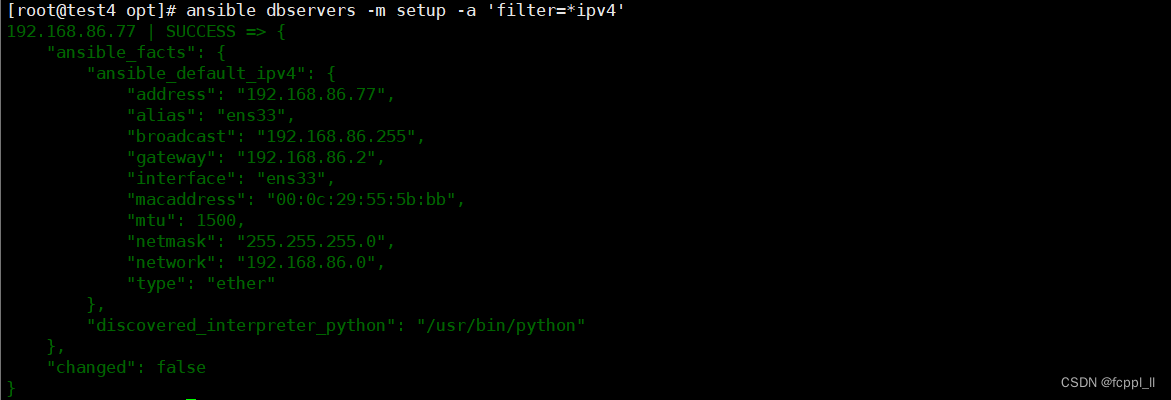
Ansible基础及模块
Ansible是一个基于Python开发的配置管理和应用部署工具,能批量配置、部署、管理上千台主机。比如以前需要切换到每个主机上执行的一或多个操作,使用Ansible只需在固定的一台Ansible控制节点上去完成所有主机的操作 Ansible是基于模块工作的,它…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
