03_51单片机点亮LED灯
51单片机是一种非常常见的单片机型号,广泛应用于各种嵌入式系统和电子设备中。LED灯是一种常见的输出设备,用于显示信息或指示状态。下面是关于51单片机控制LED灯的介绍:
1. 连接LED灯:将LED的正极连接到51单片机的一个I/O引脚,将LED的负极连接到单片机的地线(GND)。
2. 控制LED灯亮灭:在单片机程序中,通过对相应的I/O引脚进行高低电平的控制,可以实现对LED灯的亮灭操作。
3. 初始化引脚:在单片机的初始化代码中,需要将控制LED灯的I/O引脚设置为输出模式,以便能够控制LED灯的亮灭状态。
4. 控制LED灯亮度:通过控制LED灯的亮灭时间比例,可以实现对LED灯亮度的控制。可以使用延时函数来控制LED灯的闪烁频率。
5. 控制多个LED灯:如果需要控制多个LED灯,可以将它们连接到不同的I/O引脚,然后在程序中分别控制各个引脚的电平状态。
6. 控制LED灯的其他效果:除了简单的亮灭操作,还可以通过改变LED灯的亮灭模式(如闪烁、呼吸灯等)来实现更多的视觉效果。
需要注意的是,在进行单片机的LED灯控制时,要确保正确连接LED灯的极性,同时编写正确的程序代码来控制LED灯的亮灭状态。
step1:新建51单片机工程




 创建c语言文件
创建c语言文件



 修改字体的大小
修改字体的大小
 led简介:**
led简介:**
LED(Light Emitting Diode,发光二极管)是一种半导体器件,能够将电能转化为光能,实现电能到光能的直接转换。LED灯具有低功耗、高亮度、长寿命、快速反应速度等特点,因此被广泛应用于照明、显示、指示等领域。
以下是LED的一些主要特点和优势:
- 低功耗:LED灯的能效非常高,相比于传统的白炽灯和荧光灯,LED的能耗更低,能够在相同亮度的情况下节约大量电能。
- 高亮度:LED具有高亮度的特点,能够产生明亮的光线,适用于各种照明和显示应用。
- 长寿命:由于LED是固态器件,没有易损件,因此具有长寿命的优势。一般LED的寿命可达到数万小时以上,相比传统光源更加耐用。
- 快速反应速度:LED的反应速度非常快,能够在纳秒级别内进行开关操作,适用于高速通信和显示应用。
- 色彩丰富:通过不同的材料和工艺,LED能够发出不同颜色的光线,包括红、绿、蓝以及混合光色。
- 环保无污染:LED不含汞等有害物质,不会产生有害的紫外线和红外线辐射,对环境和人体健康较为友好。
- 可调光性:通过控制电流或脉冲宽度调制技术,LED能够实现可调光的功能,满足不同场景的照明需求。
由于以上的优点,LED已经广泛应用于各个领域,包括室内照明、户外照明、汽车照明、电子显示屏、指示灯、背光源等。随着技术的不断进步,LED的性能和应用将继续得到发展和拓展。
进制转换表:单片机多使用16进制进行控制

点亮led灯并将程序下载到



 具体型号要根据自己的单片机进行选择
具体型号要根据自己的单片机进行选择




下载完成后重新关闭开启单片机


相关文章:

03_51单片机点亮LED灯
51单片机是一种非常常见的单片机型号,广泛应用于各种嵌入式系统和电子设备中。LED灯是一种常见的输出设备,用于显示信息或指示状态。下面是关于51单片机控制LED灯的介绍: 1. 连接LED灯:将LED的正极连接到51单片机的一个I/O引脚&a…...

【前端设计模式】之备忘录模式
备忘录模式是一种行为设计模式,它允许在不破坏封装性的前提下捕获和恢复对象的内部状态。在前端开发中,备忘录模式可以用于保存和恢复用户界面的状态,以及实现撤销和重做功能。 备忘录模式特性: 封装了对象的状态:备…...

复习Day15:栈与队列part02:20. 有效的括号、1047.删除字符串中所有相邻重复项
我用的方法是在leetcode再过一遍例题,明显会的就复制粘贴,之前没写出来就重写,然后从拓展题目中找题目来写。辅以Labuladong的文章看。然后刷题不用CLion了,使用leetcode自带的IDE模拟面试环境。 历史博客链接: http…...

基于Java的宠物商城管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

Python的GIL存在的情况下,是否还有必要添加线程锁。
GIL锁的产生: 为了保证在单线程情况下,Python的正常执行和效率,GIL锁产生了,由于只有一把锁就不会产生死锁也不用切换。 对于Python语言而言,只有CPython解释器(用C语言编写的Python解释库)存在…...
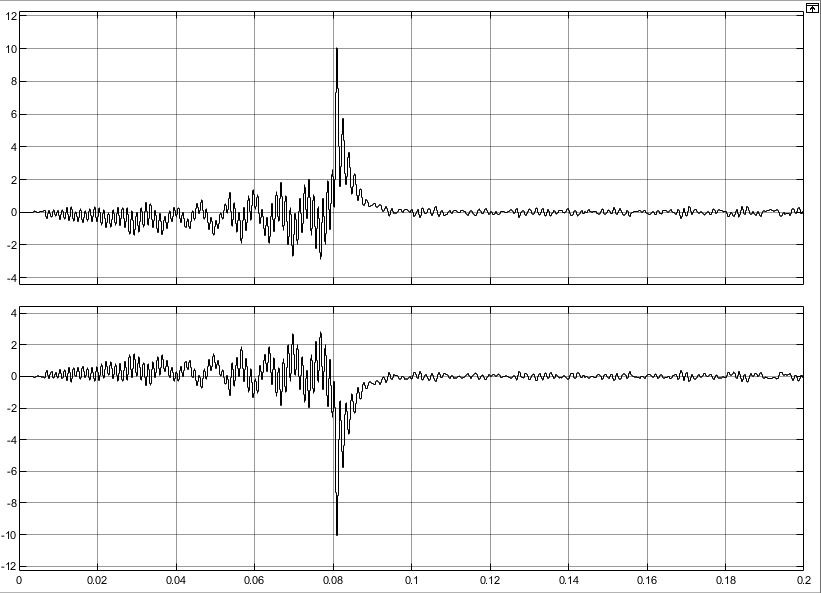
基于下垂控制的孤岛双机并联逆变器环流抑制MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 在实际应用中逆变器都是并联运行的,但是逆变器的并联运行也存在不少问题,由于线路阻抗差异、各个逆变器输出端瞬时电压幅值不同等,都容易导致环流的出现。环流会导致逆变器损耗增加,从而影响微电网的输出效率…...

spring事务面试题
1.Spring 事务实现方式有哪些? 事务就是一系列的操作原子操作,Spring事务机制主要 包括声明式事务和编程式事务。 编程式事务:通过编程的方式管理事务,自己设置未提交模式,自己获取连接,自己预编译,自己回…...

C++标准库算法整理
目录 1、数值操作 1.1、std::accumulate 1.2、std::inner_product 1.3、std::partial_sum 1.4、std::exclusive_scan 1.5、std::inclusive_scan 1.6、std::reduce 2、相邻元素 2.1、std::adjacent_difference 2.2、std::adjacent_find 2.3、std::unique 2.4、std::u…...
【待补】)
【Codeforces】Codeforces Round 903 (Div. 3)【待补】
Dashboard - Codeforces Round 903 (Div. 3) - Codeforces Problem - C - Codeforces Problem - D - Codeforces...
)
workerman 运行时报错 Call to undefined function posix_getpid()
使用 验证php扩展是否齐全 curl -Ss https://www.workerman.net/check | php缺少posix 下载 在 Linux 系统上,可以使用包管理器来安装 php-posix 扩展,例如 Ubuntu 系统可以通过以下命令进行安装: sudo apt-get install php-posix如果你使用…...

【探讨C++中的临时对象:一时之物还是永恒之道?】
在C编程中,临时对象是一个经常引起讨论的话题。它们是什么,为什么它们存在,以及如何正确使用它们?本文将深入探讨C中的临时对象,帮助您理解它们的含义和用途。 什么是临时对象? 临时对象(Temp…...
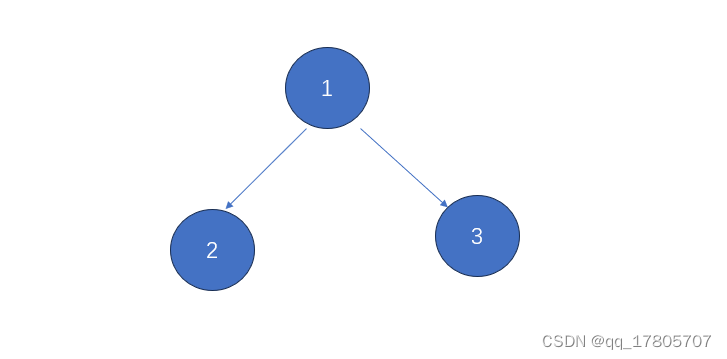
二叉树相关算法
1、二叉树基本操作 二叉树的定义就不在这里多说了,下面这个图就是一个简单的二叉树: 二叉树的三种遍历方式: 前序遍历:头左右,也就是先头后左再右:1245367 public static void prePrint(BinaryTreeNode …...

Vue_Bug npm install报错 code:128
Bug描述: npm install报错 code:128 npm ERR! Warning: Permanently added ‘github.com’ (ED25519) to the list of known hosts. npm ERR! gitgithub.com: Permission denied (publickey). npm ERR! fatal: Could not read from remote repository. n…...

【Unity ShaderGraph】| 如何快速制作一个 马赛克效果 实战
前言 【Unity ShaderGraph】| 如何快速制作一个 马赛克效果 实战一、效果展示二、马赛克效果四、应用实例 前言 本文将使用Unity 的ShaderGraph制作一个马赛克的效果,可以直接拿到项目中使用。对ShaderGraph还不了解的小伙伴可以参考这篇文章:【Unity S…...

【Java 进阶篇】JavaScript DOM Document对象详解
在前端开发中,DOM(文档对象模型)扮演着重要的角色。它允许我们使用JavaScript来与网页文档进行交互,实现动态的网页效果。DOM的核心部分之一就是Document对象,它代表了整个HTML文档。在本篇博客中,我们将深…...
按摩师,迭代出最优解(卡尔曼滤波也是类似迭代))
LetCode刷题[简单题](5)按摩师,迭代出最优解(卡尔曼滤波也是类似迭代)
所有的遍历寻求有条件约束的最大值都可以转换成,新的数带来的最大值的变化,问题往这个方向转化就可以,问题都是在最中进行选择的,因此关注的问题最大值得上限就好了,不必关注可能随机的下限。关注随机可能的下限会把问…...
C/C++笔试易错与高频题型图解知识点(二)—— C++部分(持续更新中)
目录 1.构造函数初始化列表 1.1 构造函数初始化列表与函数体内初始化区别 1.2 必须在初始化列表初始化的成员 2 引用&引用与指针的区别 2.1 引用初始化以后不能被改变,指针可以改变所指的对象 2.2 引用和指针的区别 3 构造函数与析构函数系列题 3.1构造函数与析…...

使用new创建动态结构
在运行时创建数组优于在编译时创建数组,对于结构(同一个结构可以存储多种类型的数据。)也是如此。需要在程序运行时为结构分配所需的空间,这也可以使用new运算符来完成。通过使用new,可以创建动态结构。同样࿰…...
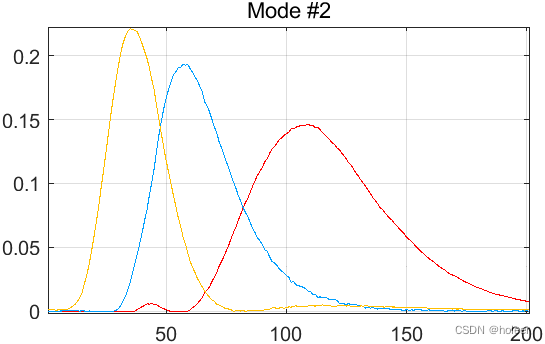
论文笔记与复现[156]PARAFAC. tutorial and applications
原文下载:https://www.sciencedirect.com/science/article/abs/pii/S0169743997000324 摘要 本文介绍了PARAFAC的多维分解方法及其在化学计量学中的应用。PARAFAC是PCA向高阶数组的推广,但该方法的一些特性与普通的二维情况截然不同。例如,…...

Python 基础30道测试题
你好,我是悦创。 我会给出 30 道涉及 Python 基础的题目。这些题目将覆盖各种 Python 基础知识点,包括数据类型、控制结构、函数、模块等。 输出 “Hello, World!”。创建一个变量,并为其赋值,然后输出该变量的值。输入两个数&a…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
