【算法挨揍日记】day15——560. 和为 K 的子数组、974. 和可被 K 整除的子数组

560. 和为 K 的子数组
560. 和为 K 的子数组
题目描述:
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。
子数组是数组中元素的连续非空序列。
解题思路:
我们可以很容易想到暴力解法,但是时间复杂度为N^2,我们可以是用前缀和对其优化
我们可以利用前缀和数组sum来记录,sum【i】代表到i位置的子数组之和
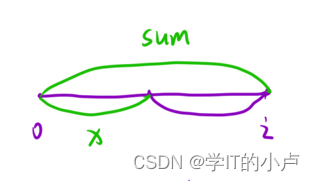
假设这是0-i的数组后面的我们先不看,我们可以将其分成两部分,一部分之和为k,另外一部分为sum【i】-k,本题是求和为k的数组的个数
那问题就可以变为在sum【i】-k中有多少个子数组等于sum【i】-k
这段区间正负都有,子区间可能不只有一个噢!!!
我们可以利用hash来完成本题,一个参数为前缀和,一个参数为次数 ,都是int类型
我们可以利用一个int变量来代替sum数组,因为sum不用每个都记录下来,只要记录上一个位置
解题代码:
class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int,int>hash;hash[0]=1;int ret=0;int sum=0;for(auto x:nums){sum+=x;if(hash.count(sum-k))ret+=hash[sum-k];hash[sum]++;}return ret;}
};974. 和可被 K 整除的子数组
974. 和可被 K 整除的子数组
题目描述:
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目。
子数组 是数组的 连续 部分。
解题思路:
解决本题我们先来补充两个知识点
- 同余定理:(a-b)/p=k....0可以转换为a%p=b%p,具体证明可见同余定理_百度百科 (baidu.com)
- C++中,负数(a)%正数(p),在C++负数求余正数正确应该为正数,但是计算结果为负数,我们对其修正时期变成a%p+p,但是为了考虑到正负统一的问题,我们再次进行修正让其变为(a%p+p)%p
接下来我们来看一下本题,本题如果你做了上一题,你会发现基本上是类似的
只不过判断条件不太一样罢了
题目要求的可以被k整除的数组为图中sum-x部分,那就变成(sum-x)%k==0也就变成了sum%k==x%k,也就转为为在【0,i-1】这个区间内有多少个前缀和的余数等于sum%k
解题代码:
class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int>hash;hash[0%k]=1;int ret=0;int sum=0;for(auto x:nums){sum+=x;int r=(sum%k+k)%k;if(hash.count(r))ret+=hash[r];hash[r]++;}return ret;}
};
相关文章:

【算法挨揍日记】day15——560. 和为 K 的子数组、974. 和可被 K 整除的子数组
560. 和为 K 的子数组 560. 和为 K 的子数组 题目描述: 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 子数组是数组中元素的连续非空序列。 解题思路: 我们可以很容易想到暴力解法…...

数字时代的探索与革新:Socks5代理的引领作用
在当今快速发展的数字时代,技术创新推动着社会的变革与进步。Socks5代理作为一项重要的网络技术,正引领着跨界电商、爬虫数据分析、企业全球化和游戏体验优化等领域的发展。本文将深入探讨Socks5代理技术在这些领域中的引领作用,以及它如何塑…...
算法-堆/归并排序-排序链表
算法-堆/归并排序-排序链表 1 题目概述 1.1 题目出处 https://leetcode.cn/problems/sort-list/description/?envTypestudy-plan-v2&envIdtop-interview-150 1.2 题目描述 2 优先级队列构建大顶堆 2.1 思路 优先级队列构建小顶堆链表所有元素放入小顶堆依次取出堆顶…...
word 如何编写4x4矩阵
百度上给的教程,打印出来没有对齐 https://jingyan.baidu.com/article/6b182309995f8dba58e159fc.html 百度上的方式试了一下,不会对齐。导致公式看起来很奇怪。 下面方式会自动对齐 摸索了一下发现可以用下面这种方式编写 4x4 矩阵。先创建一个 3x3…...
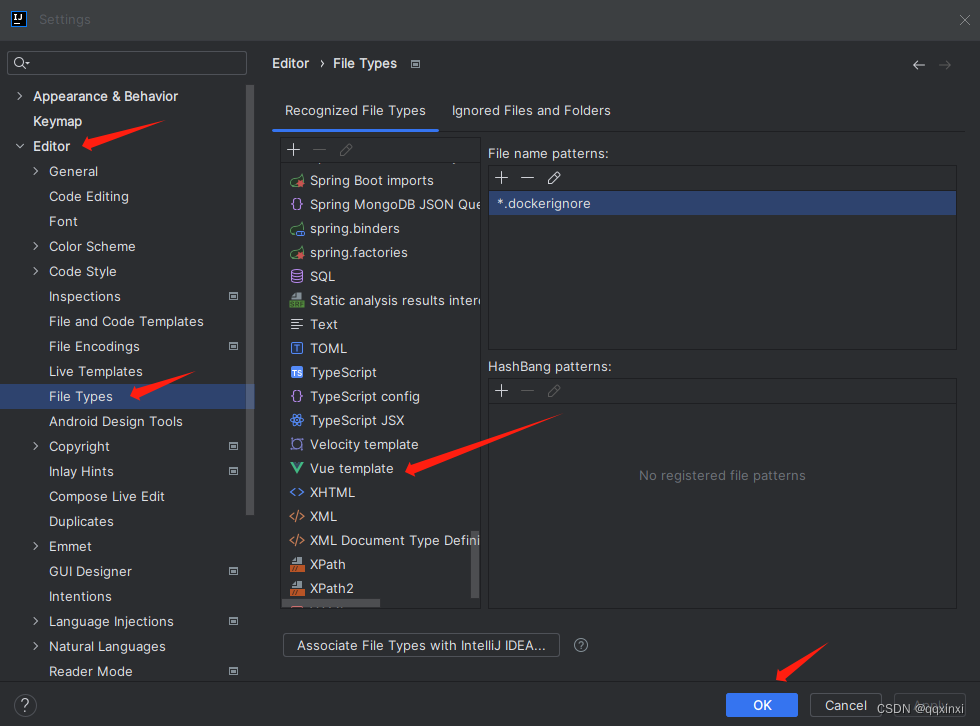
INTELlij IDEA编辑VUE项目
菜单中选择setting–>Plugins 或者快捷键 ctrlalts 搜索vue,但有些情况会搜索不出来,先说搜索到的情况 如下图所示: 如果没有vue.js则说明过去已经安装了。 搜索到了后点击Install安装即可, 但即使搜索成功了,也不…...
linux进程间通讯--信号量
1.认识信号量 方便理解:信号量就是一个计数器。当它大于0能用,小于等于0,用不了,这个值自己给。 2.特点: 信号量用于进程间同步,若要在进程间传递数据需要结合共享内存。信号量基于操作系统的 PV 操作&am…...

VS Code连接远程Linux服务器开发c++项目
1.在远程 Linux 上安装包 yum groupinstall "development tools" -y yum install cmake -y2.在 VSCode 上安装插件 C/CC/C Extension PackCMakeCMake ToolsCMake Language Support 3.连接远程Linux服务器...

stable diffusion的模型选择,采样器选择,关键词
一、Stable Diffusion的模型选择: 模型下载地址:https://civitai.com/,需要科学上网。 Deliberate:全能模型,prompt越详细生成的图片质量越好Realistic Vision:现实模型,生成仿真式图片&#…...

BI零售数据分析:以自身视角展开分析
随着零售业务不断扩展,市场竞争不断加剧,各层级的销售管理人员都急需一张能快速查看销售数据分析报表,能从中知道自己管辖内的业务最近或过去的情况,并依次为依据科学优化销售管理措施。这就要求零售数据分析报表信息足够多、数据…...
)
Maven 使用教程(三)
一、如何使用外部依赖项? 您可能已经注意到POM中的一个dependencies元素,我们一直在使用它作为示例。事实上,您一直在使用外部依赖项,但在这里我们将更详细地讨论它是如何工作的。有关更全面的介绍,请参阅我们的依赖机…...

行秋找工作的记录
2023-10-17 15:35-16:00 中移(苏州)研发中心面试 问了项目,还有一些我没准备到的Java八股文:Java类的加载过程,发射机制,redis存储结构,二叉平衡树等。但我也都没回答上来。应该无了。 2023-1…...
vue项目打包,使用externals抽离公共的第三方库
封装了一个插件,用来vue打包抽离公共的第三方库,使用unplugin进行插件开发,vite对应的功能使用了vite-plugin-externals进行二次开发 github地址 npm地址 hfex-auto-externals-plugin 自动注入插件,使用 unplugin 和 html-webpack-plugin进…...

九阳真经之各大厂校招
大学计算机系的同学要怎么努力才能校招进大厂? 秋招的大公司非常多,也是非常好的,赶上了秋招,你基本工作就敲定了,在整个应届毕业生的人群中你就占据很大的优势了。 如何准备应届校招? 一、做好规划,把…...

Go语言入门心法(五): 函数
Go语言入门心法(一): 基础语法 Go语言入门心法(二): 结构体 Go语言入门心法(三): 接口 Go语言入门心法(四): 异常体系 Go语言入门心法(五): 函数 一: go语言函数认知 函数相关认知升维:函数的功能就是把相对独立的某个相同或者时类型的功能抽象处理,使之成为一个…...

gitignore文件的语法规则
行注释:以"#"符号开头的行表示注释,Git会忽略这些行。空行:空行会被忽略。文件和目录规则: 可以使用通配符来匹配文件和目录。常用的通配符有: “*”:匹配0个或多个字符。“?”:匹配…...

vscode提示扩展主机在过去5分钟内意外终止了3次,解决方法
参考链接: https://code.visualstudio.com/blogs/2021/02/16/extension-bisect https://code.visualstudio.com/docs/setup/uninstall#_clean-uninstall 使用vscode打开jupyter notebook记事本时,窗口右下角提示扩展主机在过去5分钟内意外终止了3次 而…...
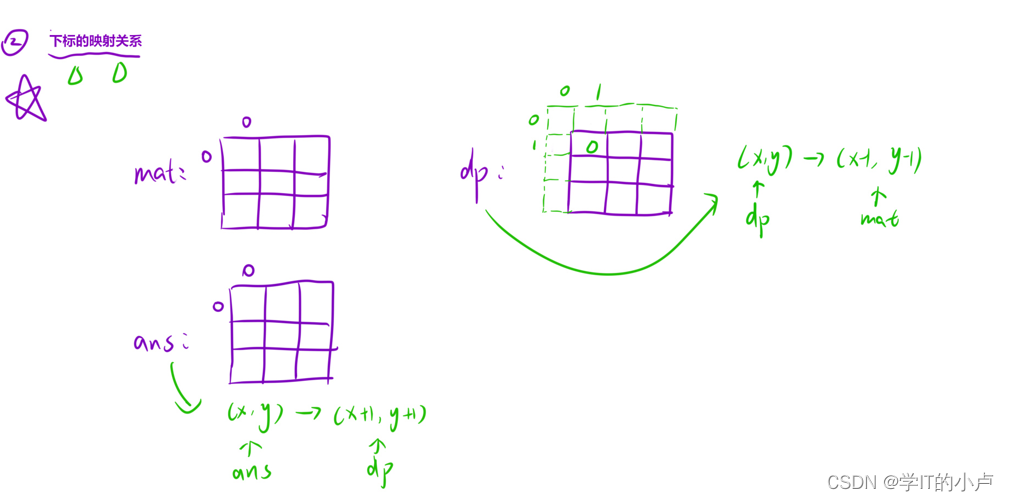
【算法挨揍日记】day16——525. 连续数组、1314. 矩阵区域和
525. 连续数组 525. 连续数组 题目描述: 给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。 解题思路: 本题的元素只有0和1,根据题目意思,我们可以把题目看成找一段最…...
k8s-13 存储之secret
Secret 对象类型用来保存敏感信息,例如密码、OAuth 令牌和 ssh key。 敏感信息放在 secret 中比放在 Pod 的定义或者容器镜像中来说更加安全和灵活 。 Pod 可以用两种方式使用 secret:作为 volume 中的文件被挂载到 pod 中的一个或者多个容器里 当 kubelet 为 pod 拉…...
)
什么是高阶成分(HOC)
高阶组件(Higher-Order Component,HOC)是一种在React中用于组件复用和逻辑抽象的设计模式。它本质上是一个函数,接受一个组件作为参数,并返回一个新的组件。 1. HOC的作用: HOC允许我们在不修改原始组件的…...

深度学习硬件配置推荐
目录 1. 基础推荐2. GPU显存与内存是一个1:4的配比?3. deep learning 入门和kaggle比赛4. 有些 Kaggle 比赛数据集很大,可能需要更多的 GPU 显存,请推荐显存4. GDDR6和HBM25. HDD 或 SATA SSD1. 基础推荐 假设您作为一个深度学习入门学者的需求,以下是一份推荐的电脑硬件配…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...