【vue2小知识】实现axios的二次封装

🥳博 主:初映CY的前说(前端领域)
🌞个人信条:想要变成得到,中间还有做到!
🤘本文核心:在vue2中实现axios的二次封装
目录
一、平常axios的请求发送方式
二、axios的一次封装
三、axios的二次封装
四、总结
【前言】我们在使用axios发送请求的时候,如果是直接使用axios用来发送我们的请求,这样的话我们需要写url、请求方式methood、如果有请求参数的话我们的axios的代码段会看起来稍微有点多并且的话我们的代码段统一的管理与后期的修改。故此在此基础上我们就需要对我们的axios进行封装来便于我们对我们接口的统一管理同时也使得代码看起来简洁。
一、平常axios的请求发送方式
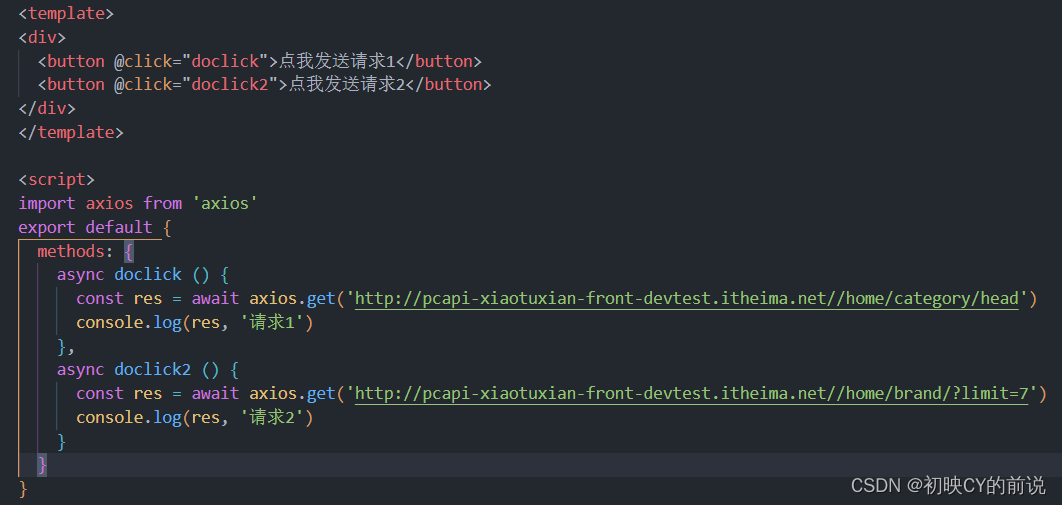
我们进页面进行发送请求见下:
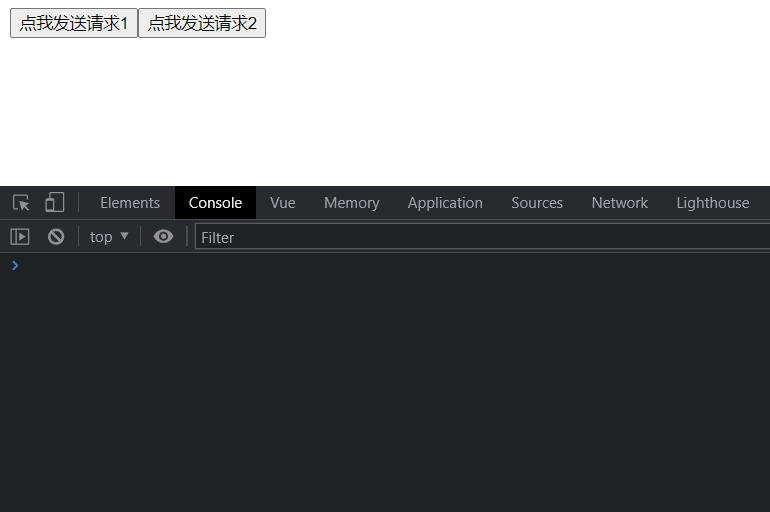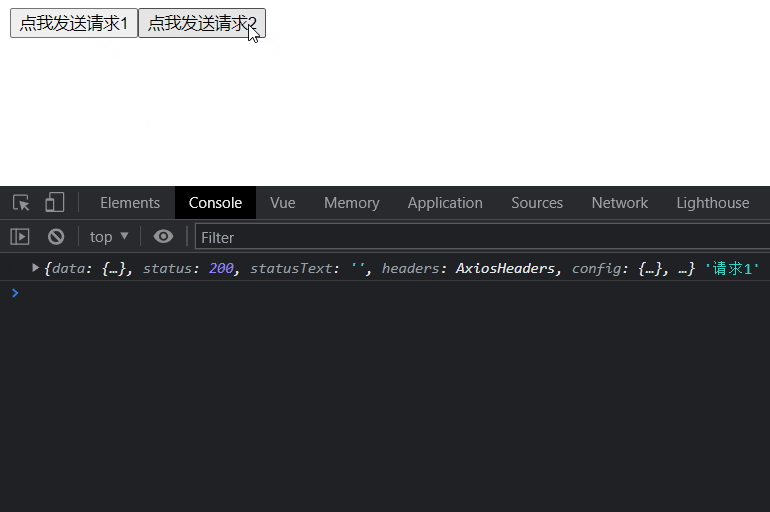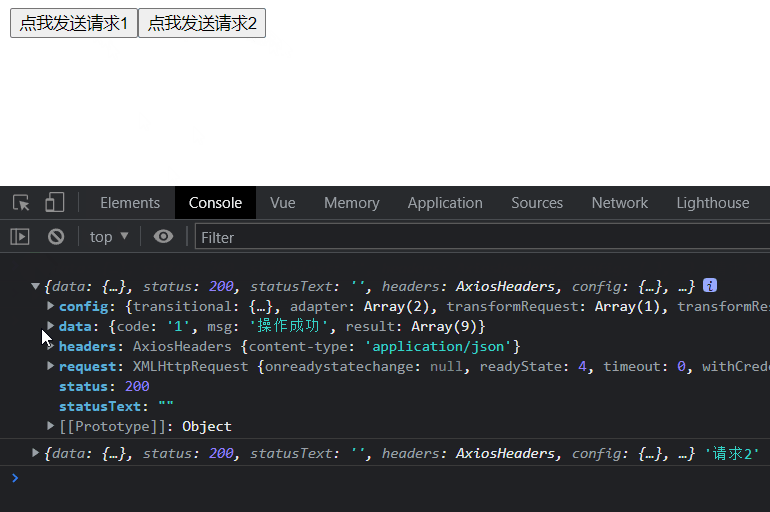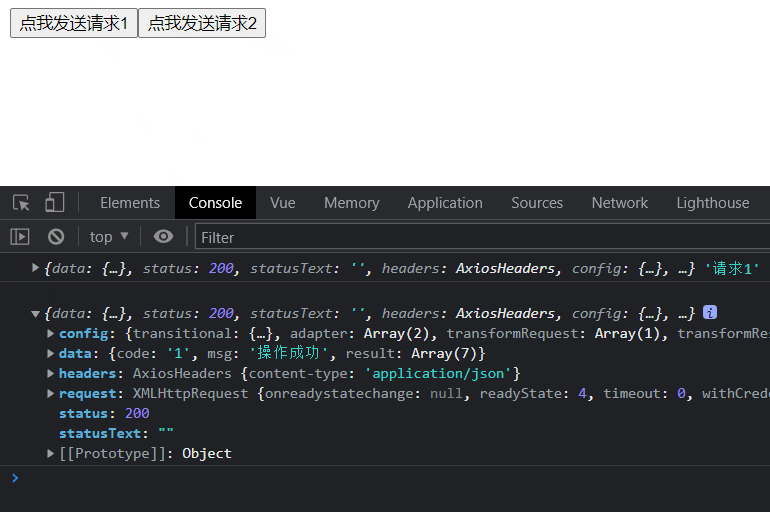
可以看到我们的请求可以成功的将我们的请求发出去并且可以收到响应。这是最基础的发送方式,我们可以看到
①我们的url中有很多重复的部分
②每个页面都这样写请求代码段多
③业务没有抽离开,不便于我们管理我们接口(多组件的时候)
综上,我们简化一下我们的请求见下↓
二、axios的一次封装
我们会在src/utils创建一个request.js的文件来存放我们的基地址与拦截器
当我们写了基地址我们每次写请求的时候就不需要写那一大段重复的代码
/* 封装axios用于发送请求 */
import axios from 'axios'/*
(1)request 相当于 Axios 的实例对象
(2)为什么要有request,而不是直接用axios* 项目开发中,有可能会有两个基地址* 不同的接口配置不同(有的要token,有的不要token)
*/
const request = axios.create({baseURL: '/home/', // 设置基地址,博主这个请求跨域了因此我设置了代理服务器,因此基地址才这么短timeout: 5000 // 请求超时:当5s没有响应就会结束请求
})// 添加请求拦截器,一下内容是axios的拦截器,可以不用写
request.interceptors.request.use(function (config) {// 在发送请求之前做些什么return config},function (error) {// 对请求错误做些什么return Promise.reject(error)}
)// 添加响应拦截器
request.interceptors.response.use(function (response) {// 对响应数据做点什么return response.data},function (error) {// 对响应错误做点什么return Promise.reject(error)}
)export default request
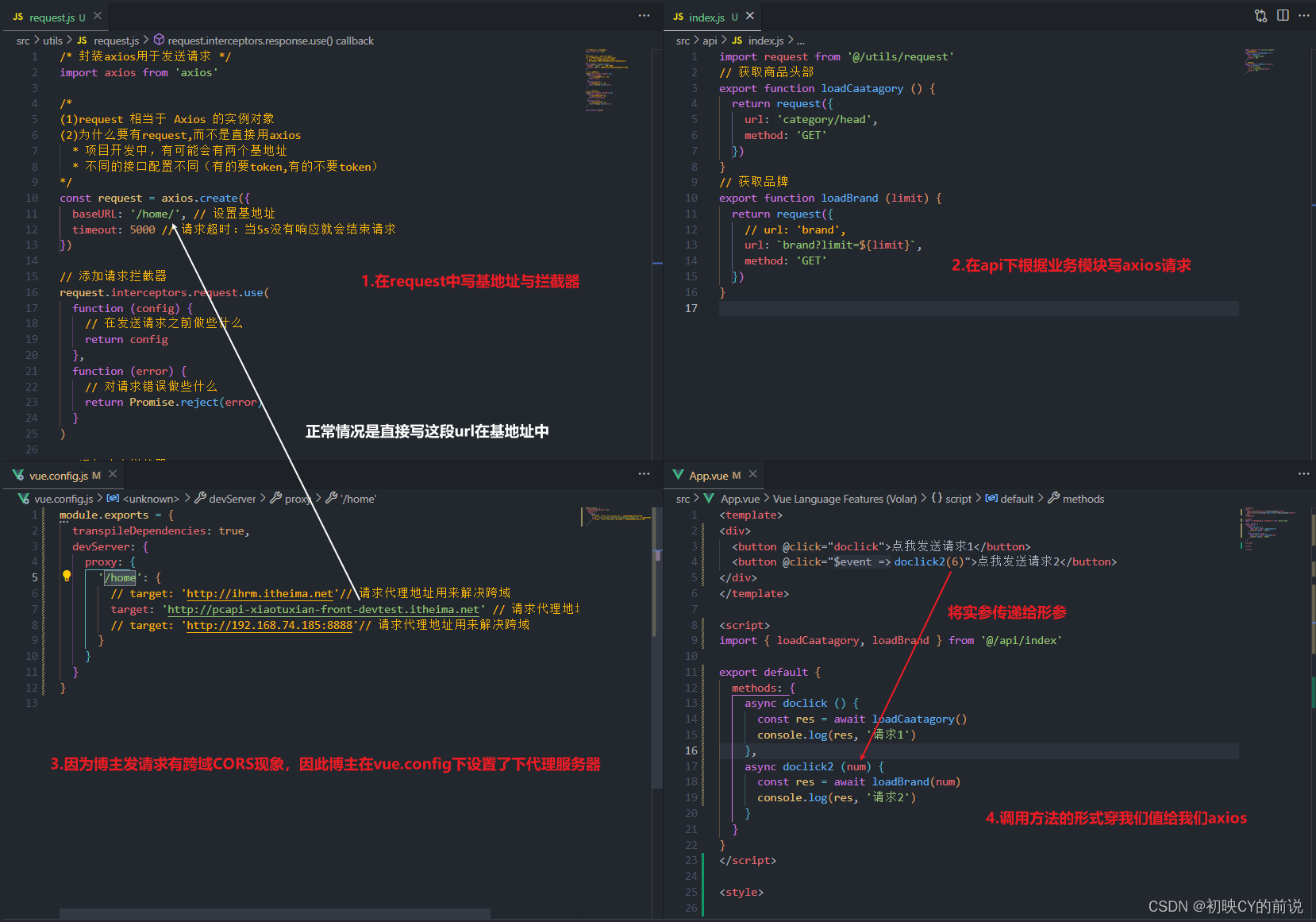
可见当我们写下了基地址之后我们就完成我们的第一次封装,引入了基地址与拦截器
三、axios的二次封装
把接口的路径写在了页面里面 : 如果接口很多,万一以后接口路径变了。怎么办呢? 一个一个文件去找是不是太麻烦了?
解决方案 : 把每一个请求接口单独封装
通俗一点来说:我们根据我们的业务来写当前页面需要的接口,这样接口便于管理。比如:我A页面需要三个接口,B页面需要五个接口。我们在一个js文件中写下八个接口吗?可以但是不推荐。
我们可以尝试将A与B两个页面的接口分离出来。
类似于这样的:
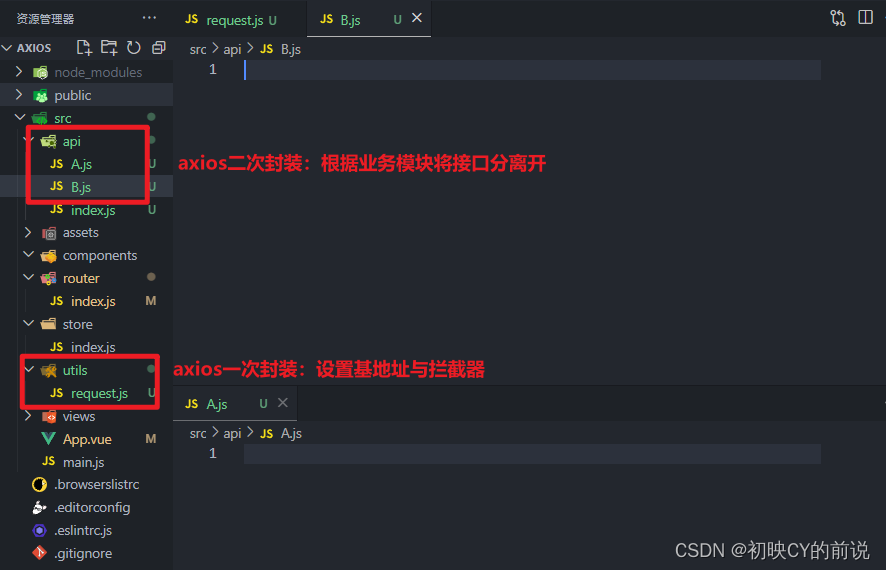
好的,基本概念了解了,我们尝试来抽离下我们的接口
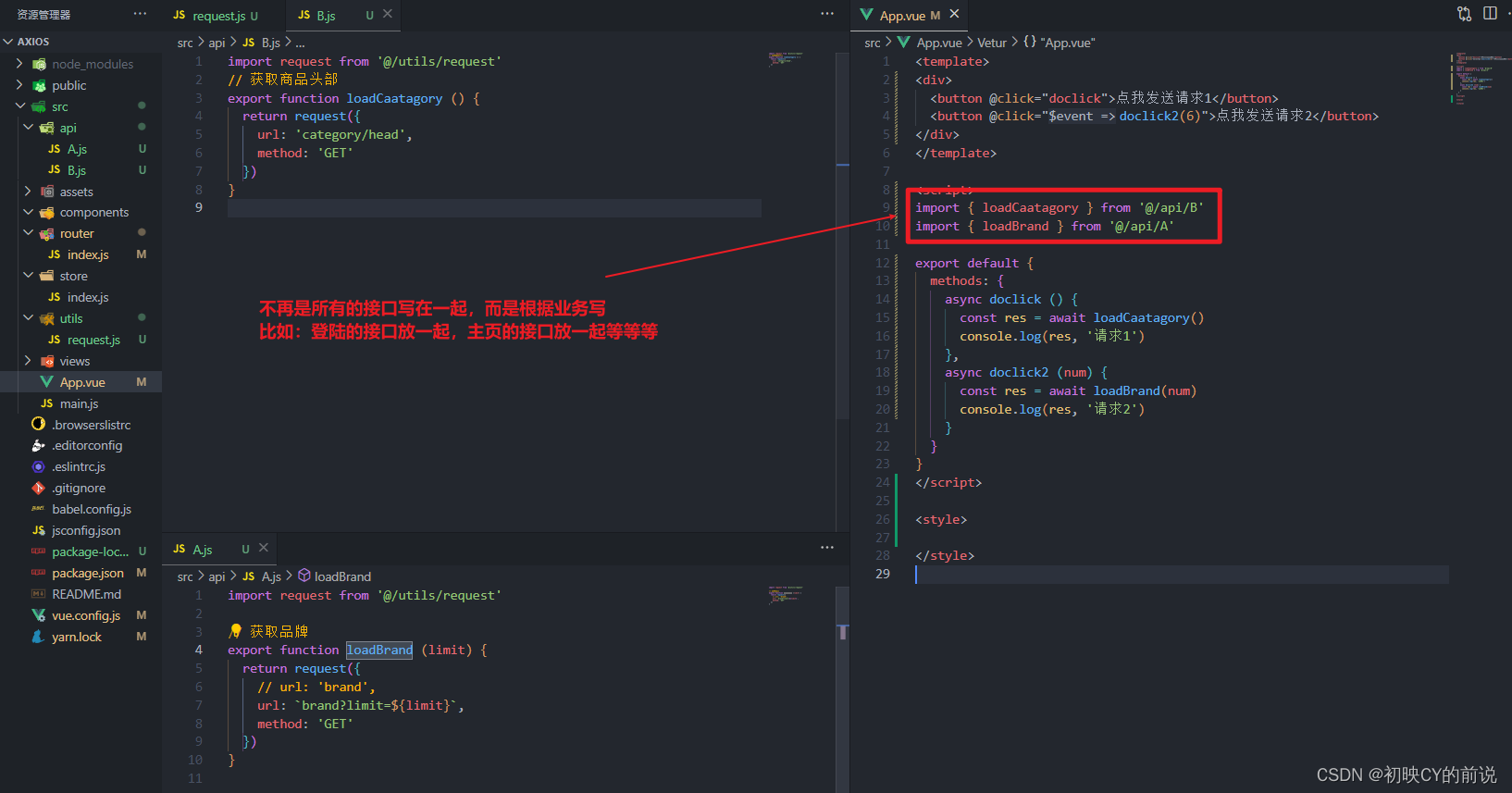
我们来测试下:
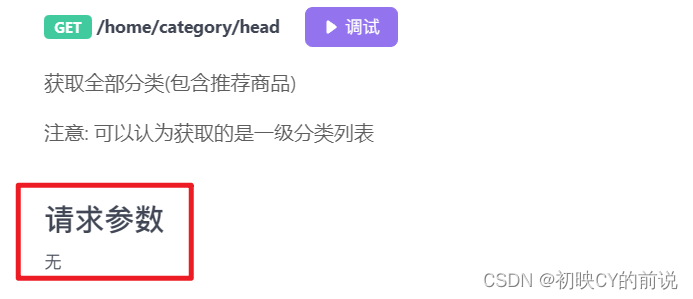
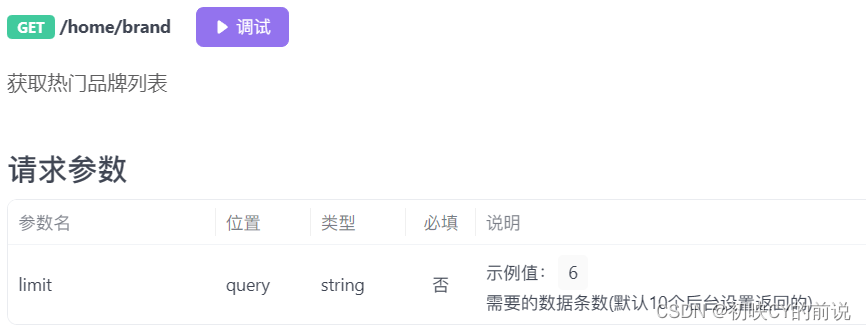
【源代码以及接口文档补充】
下面是我的接口的地址:
App.vue
<template>
<div><button @click="doclick">点我发送请求1</button><button @click="doclick2(6)">点我发送请求2</button>
</div>
</template><script>
import { loadCaatagory } from '@/api/B'
import { loadBrand } from '@/api/A'export default {methods: {async doclick () {const res = await loadCaatagory()console.log(res, '请求1')},async doclick2 (num) {const res = await loadBrand(num)console.log(res, '请求2')}}
}
</script><style></style>
A.js
import request from '@/utils/request'// 获取品牌
export function loadBrand (limit) {return request({// url: 'brand',url: `brand?limit=${limit}`,method: 'GET'})
}
B.js
import request from '@/utils/request'
// 获取商品头部
export function loadCaatagory () {return request({url: 'category/head',method: 'GET'})
}
vue.config
module.exports = {transpileDependencies: true,devServer: {proxy: {'/home': {target: 'http://pcapi-xiaotuxian-front-devtest.itheima.net' // 请求代理地址用来解决跨域}}}
}
四、总结
我们封装axios是为了将我们的接口根据模块的不同而分离开来,便于我们的管理。
第一次封装:提取公共部分
第二次封装:根据业务模块分离接口
愿你有所收获,本文就此结束!
相关文章:

【vue2小知识】实现axios的二次封装
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:在vue2中实现axios的二次封装 目录 一、平常axios的请求发送方式 二、axios的一次封装…...

走近php的数组:数组的定义与数组函数
数组是一种数据结构,它由一组元素组成,这些元素可以是相同类型或不同类型。数组是在程序运行时动态创建的,可以根据需要增加或删除元素,因此它们是非常灵活和实用的数据结构。在大多数编程语言中,数组都有一个索引&…...
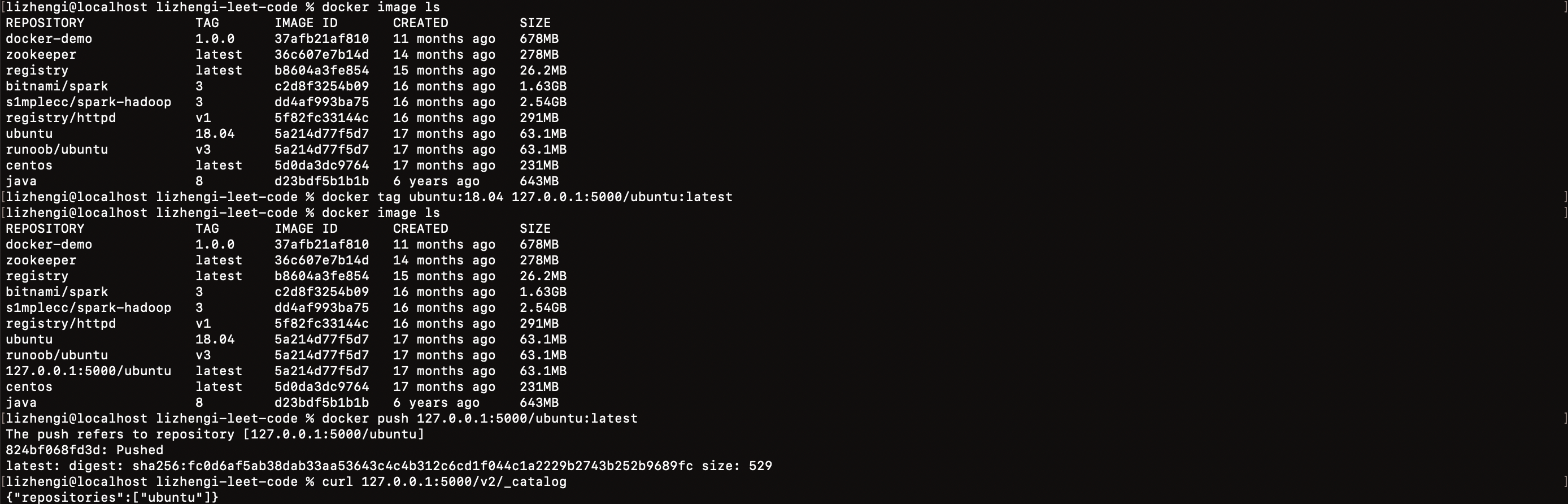
Docker 应用实践-仓库篇
目前 Docker 官方维护了一个公共仓库 Docker Hub,用于查找和与团队共享容器镜像,界上最大的容器镜像存储库,拥有一系列内容源,包括容器社区开发人员、开放源代码项目和独立软件供应商(ISV)在容器中构建和分…...
python+django篮球NBA周边商城vue
目 录 第一章 绪 论 1 1.1背景及意义 1 1.2国内外研究概况 1 1.3 研究的内容 1 第二章 关键技术的研究 3 2.1 vue技术介绍 3 myproject/ <-- 高级别的文件夹 |-- myproject/ <-- Django项目文件夹 | |-- myproje…...
抽象类与接口的区别
抽象类什么是抽象类?抽象类是特殊的类,只是不能被实例化;除此以外,具有类的其他特性;重要的是抽象类可以包括抽象方法,这是普通类所不能的。抽象方法只能声明于抽象类中,且不包含任何实现&#…...

1904. 你完成的完整对局数
题目: 一款新的在线电子游戏在近期发布,在该电子游戏中,以 刻钟 为周期规划若干时长为 15 分钟 的游戏对局。这意味着,在 HH:00、HH:15、HH:30 和 HH:45 ,将会开始一个新的对局,其中 HH 用一个从 00 到 23…...

Vue3:自定义指令以及简单的后台管理权限封装
目录 前言: 自定义指令介绍: 局部的自定义指令: 全局自定义指令: 讲讲后台管理权限管理: 前言: 说起这个自定义指令的使用场景,我第一反应就是,后台管理的权限管理,要…...
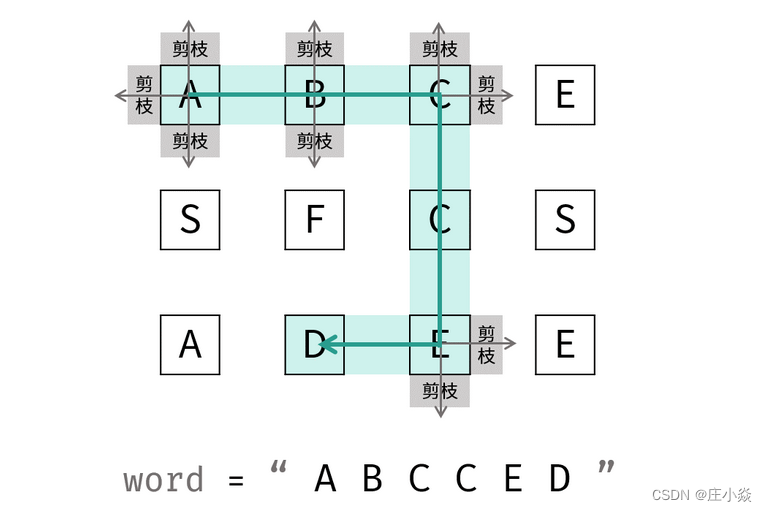
剑指 Offer 12. 矩阵中的路径
摘要 剑指 Offer 12. 矩阵中的路径 一、回溯算法解析 本问题是典型的矩阵搜索问题,可使用 深度优先搜索(DFS) 剪枝解决。 深度优先搜索: 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归,先朝一个方向搜…...
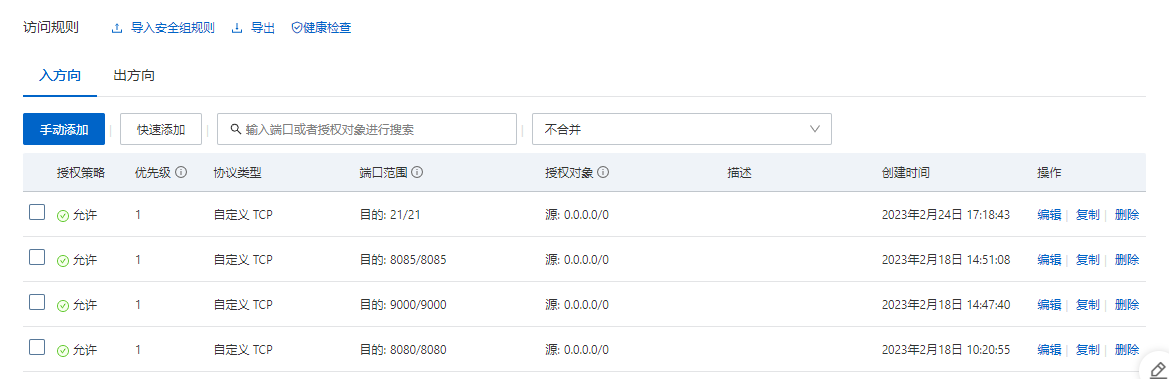
springboot+jersey+tomcat实现跨域方式上传文件到服务器
前言 在服务器上,当我们启动了tomcat,就可以以 http://ip地址:8080/文件路径/文件名 的方式,进行访问到我们服务器上处于tomcat的webapps文件夹下的文件 于是为了可以往上面加文件,我们有两种方式,一种就是直接复制文…...

【微信小程序】-- 常用视图容器类组件介绍 -- view、scroll-view和swiper(六)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &#…...
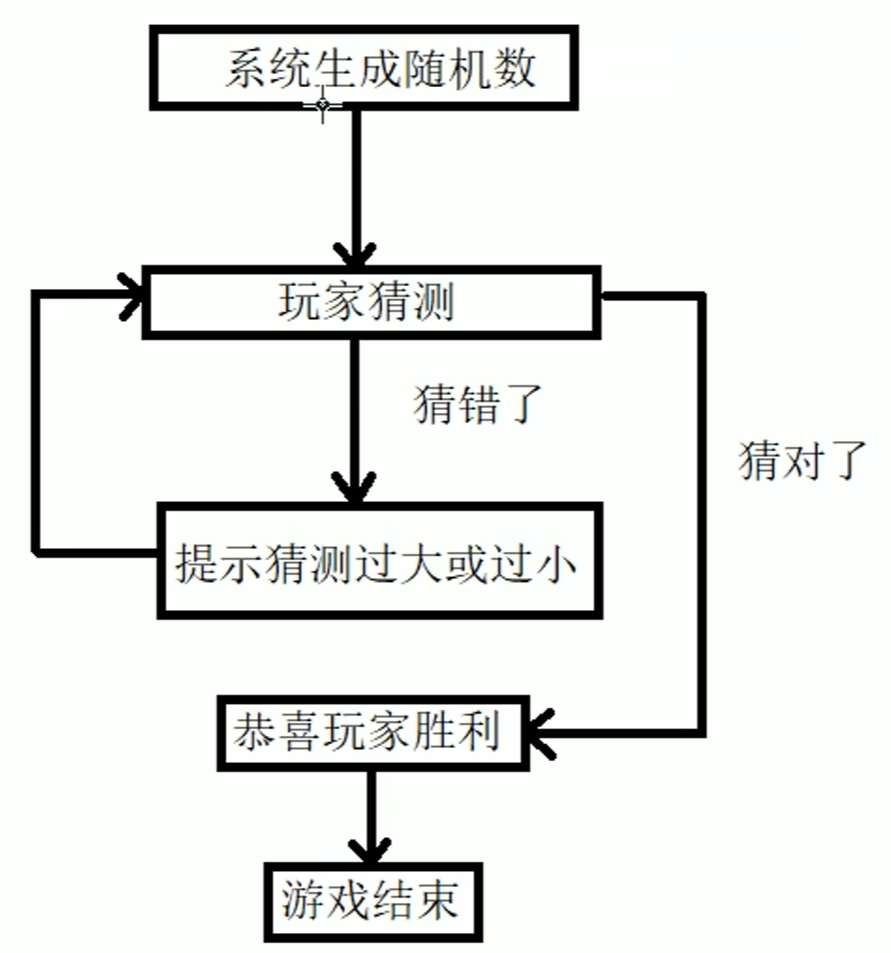
猜数字游戏——C++
我们在有了一定的C基础了以后,简单的实现一个案例(其实只要会while循环结构就行了),我们本章内容会实现猜数字游戏,大家有什么语法疑问可以看看我写的:C快速入门_染柒_GRQ的博客-CSDN博客,该博客…...

整数对最小和
题目描述 给定两个整数数组 array1 array2。数组元素按升序排列,假设从array1 、array2中分别取出一个元素可构成一对元素,现在需要取出K个元素并对取出的所有元素求和,计算和的最小值 注意事项 两对元素如果对应于array1 array2中的两个下…...

2023-2-22 -javaagent
周三,天气晴,7度 Java Agent Java Agent也叫作java探针,可以实现动态修改java字节码,完成额外的功能。在java类编译成字节码,在jvm执行之前,它可以读取修改字节码,以来完成额外的功能。 使用…...

JavaScript BOM操作
目录 前言 window 对象 location 对象 navigator 对象 screen 对象 history 对象 前言 BOM(Browser Object Model)指的是浏览器对象模型,它是 JavaScript 和浏览器之间的接口。通过 BOM,JavaScript 可以与浏览器窗口交互&…...

【机器学习 | 强基计划】开山篇 | 机器学习介绍及其类别和概念阐述
🤵♂️ 个人主页: @计算机魔术师 👨💻 作者简介:CSDN内容合伙人,全栈领域优质创作者。 机器学习 | 强基计划系列 (一) 作者: 计算机魔术师 版本: 1.0 ( 2022.2.25) 注释:文章会不定时更新补充 文章目录 前言一、机器学习概览1.1 有监督学习和无监督学习1.1.…...
)
华为OD机试真题Java实现【合规数组】真题+解题思路+代码(20222023)
合规数组 题目 给定一个正整数数组 检查数组中是否存在满足规则的数组组合 规则: A = B + 2C 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Java)真题目录汇总 ## 输入 第一行输出数组的元素个数 接下来一行输出所有数组元素,用空格隔开 输出 如果存在满…...

BoostSearcher搜索引擎项目
BoostSearcher搜索引擎项目 1.BoostSearcher这个项目是什么? 答:一个为Boost文档建立索引的站内搜索引擎,简单的说就是一个类似于csdn站内文档搜索框。 项目展示: gitee:https://gitee.com/zxlfx/boost-search-engine-project …...
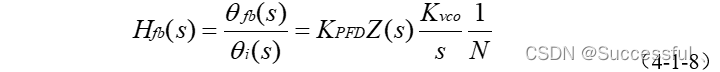
【模拟集成电路】频率综合器(Frequency Synthesizer,FS)设计
应用于无线局域网的频率综合器设计前言频率综合器简介各部分链接链接:前言 本文主要内容是对频率综合器或称为PLL 做出简单介绍,为课程设计部分章节内容,后需给出各部分的设计方案,以及测试结果。 频率综合器简介 无线收发系统中…...
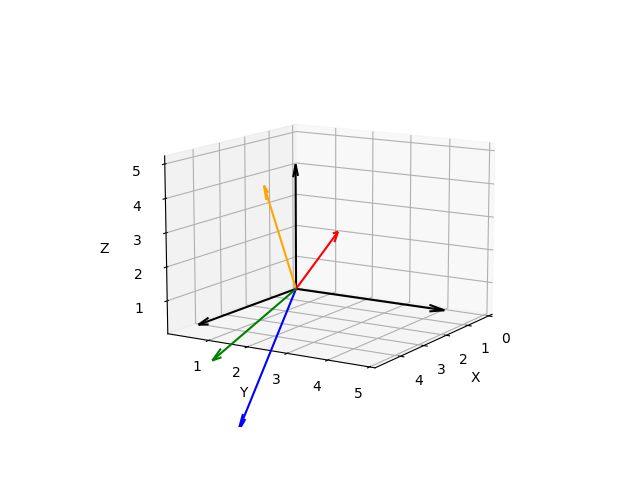
实例8:机器人的空间描述和变换仿真
实例8:机器人的空间描述和变换仿真 实验目的 通过刚体与刚体的平动、转动基础知识的学习,熟悉位姿的描述通过Python编程实践,可视化学习坐标系的变换,熟悉空间变换 实验要求 通过python编程,输入一指定向量和对应的…...

网络 导航
目录内容链接网络网络参考文章:【网络】http请求 调试网络问题解决参考文章:【问题解决】网络 IP DNS解析网络问题解决参考文章:【问题解决】网络 TCP 规则 抓包网络问题解决参考文章:【问题解决】网络 Http请求 调试网络问题解决…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
