机器学习-无监督学习之聚类
文章目录
- K均值聚类
- 密度聚类(DBSCAN)
- 层次聚类
- AGNES 算法
- DIANA算法
- 高斯混合模型聚类
- 聚类效果的衡量指标
- 小结
K均值聚类
- 步骤:
Step1:随机选取样本作为初始均值向量。
Step2:计算样本点到各均值向量的距离,距离哪个最近就属于哪个簇
Step3:重新计算中心点作为均值向量,重复第二步直到收敛 - 常见距离
- 曼哈顿距离(街区距离)
- 欧氏距离
- 切比雪夫距离(棋盘距离)
- 闵氏距离(结合前三种)
- 余弦相似度
- 适用场景:塔吊和文本分析
- 汉明距离
- 适用场景:计算机网络中二进制纠错
- 没有哪个距离最好,只有哪个距离最合适,这就是理解这么多距离的原因
密度聚类(DBSCAN)
- 概念:
- 给定数据集D={x1,x2,…,xm}
- 邻域ε:对x∈D,其ε邻域包含样本集D中与x的距离不大于ε的样本
- 核心对象:若x的ε邻域至少包含MinPts个样本,即|N(x)|≥MinPts,则x是一个核心对象。
N ( x ) = { x ′ ∈ D ∣ dist ( x , x ′ ) ≤ ε } N(x) = \{x' \in D \mid \text{dist}(x, x') \leq \varepsilon\} N(x)={x′∈D∣dist(x,x′)≤ε}
- 密度直达、密度可达、密度相连
层次聚类
应用:生物领域
AGNES 算法
- 思想类似归并排序,自底向上
Step1:先将每个样本当成一个簇
Step2:然后将距离最近的两个簇进行合并
Step3:重复Step2
直到,最远的两个簇的距离超过阈值或簇的个数达到指定值 - 距离:最大距离、最小距离、平均距离
DIANA算法
- 思想类似快速排序,自顶向下
Step1:初始化,所有样本集中归为一个簇
Step2:在同一个簇中,计算任意两个样本之间的距离,找到距离最远的两个样本点a,b,
将a,b作为两个簇的中心:
Step3:计算原来簇中剩余样本点距离a,b的距离,距离哪个中心近,分配到哪个簇中
Step4:重复步骤2、3
直到,最远两簇距离不足阈值,或者簇的个数达到指定值,终止算法
高斯混合模型聚类
- 应用:将混合的连个数据集分开
- 一维高斯函数,多元独立高斯函数
- 正态分布就是高斯函数
f ( x ) = 1 ( 2 π ) d / 2 ⋅ ∣ Σ ∣ 1 / 2 ⋅ exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) f(x) = \frac{1}{(2\pi)^{d/2} \cdot |\Sigma|^{1/2}} \cdot \exp\left(-\frac{1}{2}(x - \mu)^T \Sigma^{-1} (x - \mu)\right) f(x)=(2π)d/2⋅∣Σ∣1/21⋅exp(−21(x−μ)TΣ−1(x−μ)) - 高斯混合模型:
f ( x ) = ∑ i = 1 K w i ⋅ 1 ( 2 π ) d / 2 ⋅ ∣ Σ i ∣ 1 / 2 ⋅ exp ( − 1 2 ( x − μ i ) T Σ i − 1 ( x − μ i ) ) f(x) = \sum_{i=1}^{K} w_i \cdot \frac{1}{(2\pi)^{d/2} \cdot |\Sigma_i|^{1/2}} \cdot \exp\left(-\frac{1}{2}(x - \mu_i)^T \Sigma_i^{-1} (x - \mu_i)\right) f(x)=i=1∑Kwi⋅(2π)d/2⋅∣Σi∣1/21⋅exp(−21(x−μi)TΣi−1(x−μi))
Step1:将参数随机初始化
Step2:计算x_j由各混合成分生成的后验概率,即观测数据x_j由第i个分模型生成的概率p(z_j=i|x_j)并记为γ_ji
Responsibility ( x i , θ ) = π k ⋅ N ( x i ∣ μ k , Σ k ) ∑ j = 1 K π j ⋅ N ( x i ∣ μ j , Σ j ) \text{Responsibility}(x_i, \theta) = \frac{\pi_k \cdot \mathcal{N}(x_i | \mu_k, \Sigma_k)}{\sum_{j=1}^{K} \pi_j \cdot \mathcal{N}(x_i | \mu_j, \Sigma_j)} Responsibility(xi,θ)=∑j=1Kπj⋅N(xi∣μj,Σj)πk⋅N(xi∣μk,Σk)
Step3:利用γ_ji计算新均值
Step4:利用γ_ji计算新标准差
Step5:利用γ_ji计算新权值
Step6:重复Step2-5直到收敛 - 最大似然函数思想
聚类效果的衡量指标
- 目的:评估聚类结果是否好坏,确立优化目标
- 结论:簇内彼此相似,簇间彼此不同
- 指标(是否用到样本均值):
- 外部指标:JC指数、FMI指数、RI指数
- 内部指标:DB指数,Dunn指数
小结
- 没有最优的算法,只有最合适的算法。
参考书:周志华-机器学习-西瓜书
相关文章:

机器学习-无监督学习之聚类
文章目录 K均值聚类密度聚类(DBSCAN)层次聚类AGNES 算法DIANA算法 高斯混合模型聚类聚类效果的衡量指标小结 K均值聚类 步骤: Step1:随机选取样本作为初始均值向量。 Step2:计算样本点到各均值向量的距离,…...

智能垃圾桶丨悦享便捷生活
垃圾桶是人们日常生活所必不可少的必需品,它让生活中所产生的垃圾有了一个正确的存放地方。随着生产技术的迅速发展,垃圾桶也得以更新换代。由最初的简单式的圆筒式垃圾桶,到现在出现的感应式垃圾桶、智能语音控制垃圾桶,垃圾桶也…...

【数据结构】线性表(一)线性表的定义及其基本操作(顺序表插入、删除、查找、修改)
目录 一、线性表 1. 线性表的定义 2. 线性表的要素 二、线性表的基本操作 三、线性表的顺序存储结构 1. 定义 2. 顺序表的操作 a. 插入操作 b. 删除操作 c. 查找操作 d. 修改操作 e. 代码实例 一、线性表 1. 线性表的定义 一个线性表是由零个或多个具有相同…...

MyBatis的自定义插件
MyBatis的自定义插件 前置知识 MyBatis 可以拦截的四大组件 Executor - 执行器StatementHandler - SQL 语句构造器ParameterHandler - 参数处理器ResultSetHandler - 结果集处理器 自定义 MyBatis 插件 /*** 打印 sql 执行的时间插件*/ Intercepts(// 指定拦截器拦截的对象…...

生物制剂\化工\化妆品等质检损耗、制造误差处理作业流程图(ODOO15/16)
生物制剂、化工、化妆品等行业,因为产品为液体,产品形态和质量容易在各个业务环节发生变化,常常导致实物和账面数据不一致,如果企业业务流程不清晰,会导致系统大量的库存差异,以及财务难以核算的问题&#…...

vbv介绍
VBV模型 VBV即Video Buffer Verifier(视频缓冲区校验器)。 本质是encoder端的一个虚拟buffer,可以将VBV当做一个容量受限的管道,有一个上限容量值和下限容量值,在经过此管道的调节之后能限制编码码率在上限容量值和下限容量值之间。VBV对标NetEq中的那几个buffer(decoder b…...

Linux CentOS 8(网卡的配置与管理)
Linux CentOS 8(网卡的配置与管理) 目录 一、项目介绍二、命令行三、配置文件四、图形画界面的网卡IP配置4.1 方法一4.2 方法二 一、项目介绍 Linux服务器的网络配置是Linux系统管理的底层建筑,没有网络配置,服务器之间就不能相互…...

python -m pip install 和 pip install 的区别解析
python -m pip install 和 pip install 的区别解析 python -m pip install 使用了 -m 参数来确保以 Python 模块的形式运行 pip,适用于确保在不同的环境中正确使用 pip,这篇文章主要介绍了python -m pip install 和 pip install 的区别,需要的朋友可以参…...

深度解读js中数组的findIndex方法
js中数组有一个findIndex方法,这个方法是一个让人感到很困惑的方法。 首先来看看MDN对这个方法的解释:Array.prototype.findIndex() - JavaScript | MDN The findIndex() method of Array instances returns the index of the first element in an arra…...
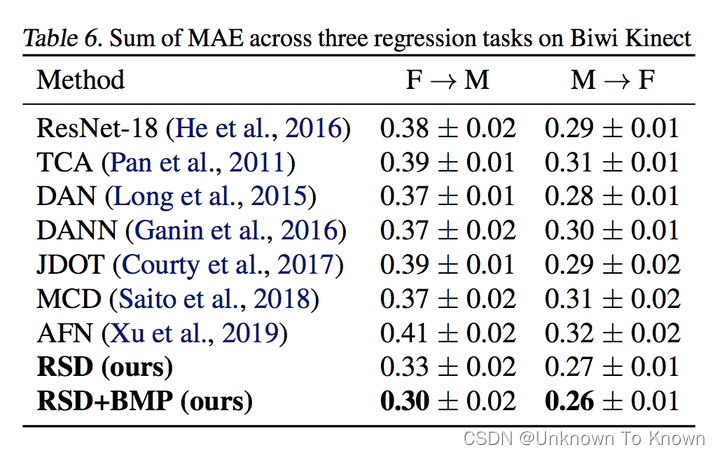
ICML2021 | RSD: 一种基于几何距离的可迁移回归表征学习方法
目录 引言动机分析主角(Principal Angle)表征子空间距离正交基错配惩罚可迁移表征学习实验数据集介绍 实验结果总结与展望 论文链接 相关代码已经开源 引言 深度学习的成功依赖大规模的标记数据,然而人工标注数据的代价巨大。域自适应&…...

中国人民大学与加拿大女王大学金融硕士:在该奋斗的岁月里,对得起每一寸光阴
在这个快速变化的世界中,金融行业面临不断更新的挑战和机遇。为了应对这些挑战,中国人民大学与加拿大女王大学合作举办金融硕士项目,旨在培养具有国际视野、扎实的金融理论基础和实战经验的专业人才。 中国人民大学和加拿大女王大学金融硕士…...

Python基础教程:装饰器的详细教程
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 一、什么是装饰器 目的:给func()方法,增加一个功能,在fun()执行期间,同时把fun()执行速率机算出来 import time def func():print(嘻嘻哈哈)start_time time.time() ti…...

Apache poi xwpf word转PDF中文显示问题解决
原问题解决方法:https://github.com/opensagres/xdocreport/issues/161 POM依赖 <properties><java.version>1.8</java.version><poi.version>3.14</poi.version></properties><dependencies><dependency><gro…...

Gartner发布2024年十大战略技术趋势
今日,Gartner发布了2024年企业机构需要探索的十大战略技术趋势。这十大趋势包括:全民化的生成式;AI 信任、风险和安全管理;AI 增强开发;智能应用;增强型互联员工队伍;持续威胁暴露管理ÿ…...

在UniApp中使用uni.makePhoneCall方法调起电话拨打功能
目录 1.在manifest.json文件中添加权限 2. 组件中如何定义 3.如何授权 4.相关知识点总结 1.在manifest.json文件中添加权限 {"permissions": {"makePhoneCall": {"desc": "用于拨打电话"}} }2. 组件中如何定义 <template>…...
苹果手机怎么刷机?掌握好这个方法!
苹果手机以其优秀的性能与高颜值的设计赢得了一大批用户的喜爱。但是,当手机使用久了以后,难免会出现一些系统问题。在遇到运行不稳定、忘记锁屏密码、软件故障、频繁死机等情况时,我们可能需要对手机进行刷机来解决问题。那么,苹…...

最新ai创作系统CHATGPT系统源码+支持GPT4.0+支持ai绘画(Midjourney)
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统AI绘画系统,支持OpenAI GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署…...

代码随想录算法训练营Day56|动态规划14
代码随想录算法训练营Day56|动态规划14 文章目录 代码随想录算法训练营Day56|动态规划14一、1143.最长公共子序列二、 1035.不相交的线三、53. 最大子序和 动态规划 一、1143.最长公共子序列 class Solution {public int longestCommonSubsequence(String text1, String text2…...
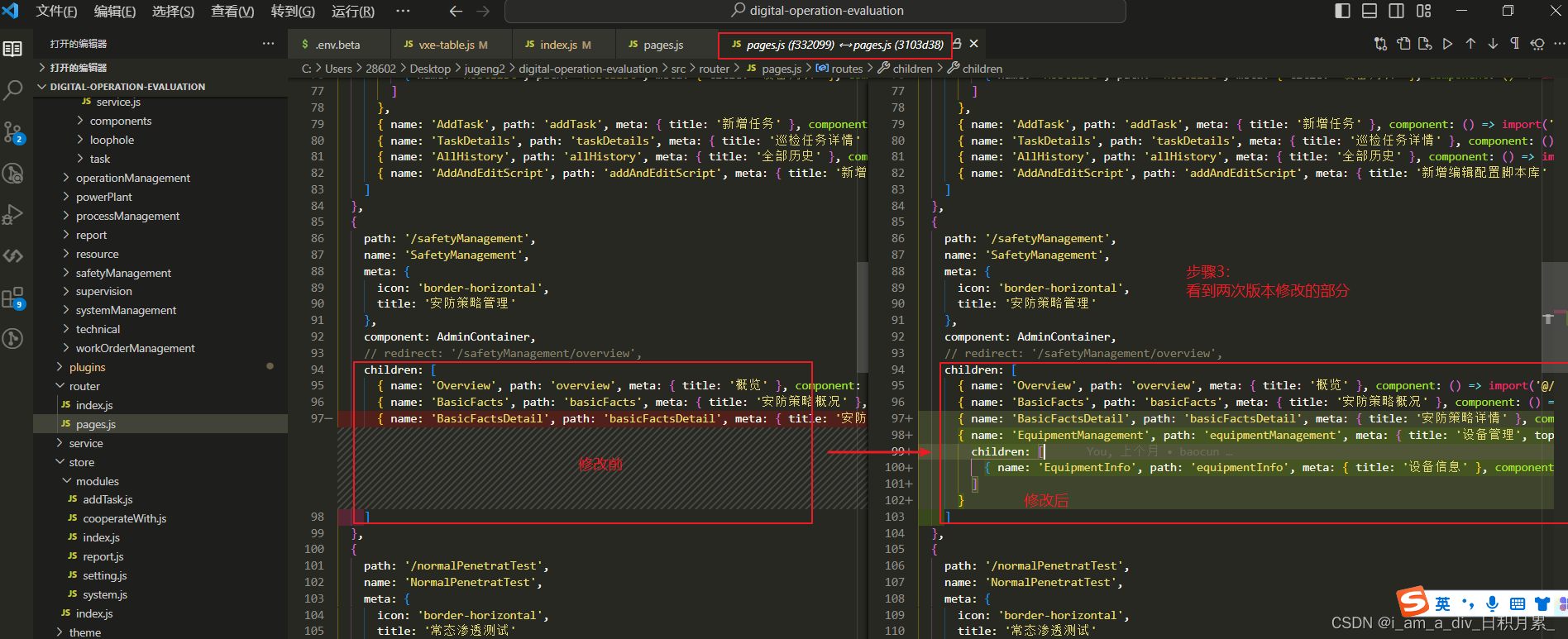
VsCode通过Git History插件查看某个页面的版本修改记录
首先需要安装插件Git History 方式一:通过 点击File History 查看某个文件变更;即通过commit的提交记录去查看某个文件的修改 方式二:通过点击选择toggle File Blame 查看当前页面每一行所有提交修改记录...
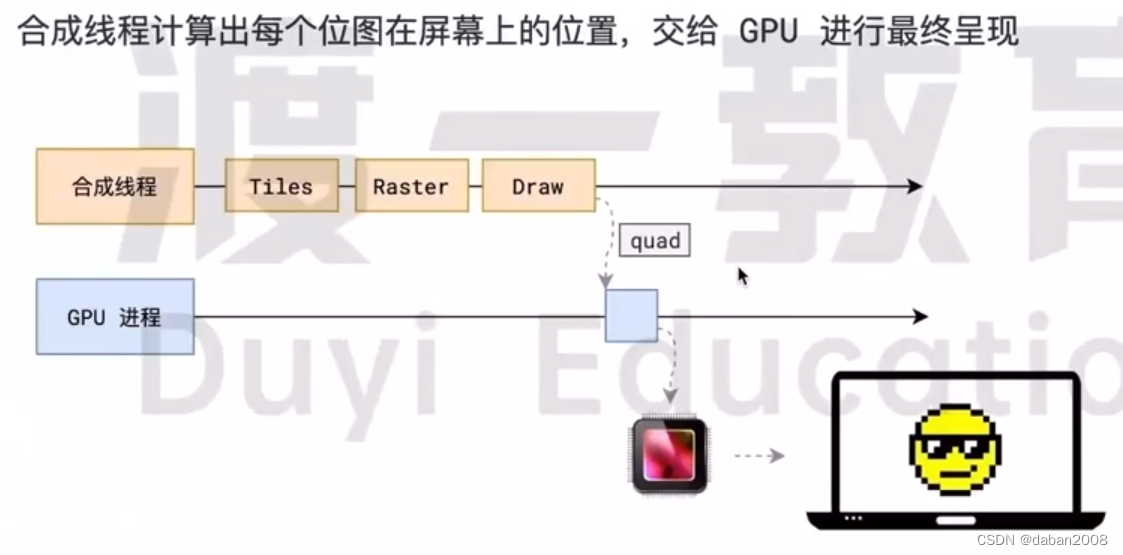
事件循环(渡一)
一、事件循环 浏览器有哪些进程和线程 浏览器是一个多进程多线程的应用程序,当启动浏览器后,会默认启动多个进程 可以在浏览器任务管理器中查看所有进程 其中最主要的进程有: 浏览器进程 主要负责界面展示,用户交互,…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...
