二叉树的前 中 后序的非递归实现(图文详解)

🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:非递归实现二叉树的前中后序遍历.
金句分享:
✨不要慌,不要慌,太阳下了,有月光!✨
前言
为什么要掌握非递归呢?
递归实现前中后序遍历十分轻松,二非递归就复杂许多了.
主要是递归有以下几个缺陷:
-
内存消耗:递归算法由于会在堆栈中不停地压入和弹出函数调用记录,因此会占用大量的内存,如果递归的次数过多,可能会导致栈溢出。
-
效率低下:递归算法的效率低下,因为每次递归都需要重新压入调用记录和恢复上一次的状态,这些操作都会增加额外的开销,导致递归算法效率低下,特别是在处理大量数据时会更为明显。
-
可读性较差:递归算法的代码一般会比较复杂,理解和维护难度较大,而且递归算法往往涉及到栈的使用,在理解和分析时需要一定的数学基础。
总结:主要害怕栈溢出,其次,可以增加一点点效率.
一、非递归实现"前序遍历"
题目链接:传送门
题目要求:
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
补充知识:
二叉树的前序遍历,又称为先序遍历,是指先访问节点本身,然后按照先左后右的顺序遍历其左右子树。具体步骤如下:
- 访问根节点。
- 遍历左子树,即对左子节点进行前序遍历。
- 遍历右子树,即对右子节点进行前序遍历。
方法一、思路分析:

- 根节点入栈.
- 栈顶元素入存入
vector,根节点出栈. - 右孩子入栈
- 左孩子入栈
因为我们要求:
先访问左孩子,再访问右孩子.
而栈是后进先出的结构,所以:
右孩子先入栈,左孩子后入栈.
步骤示例图:
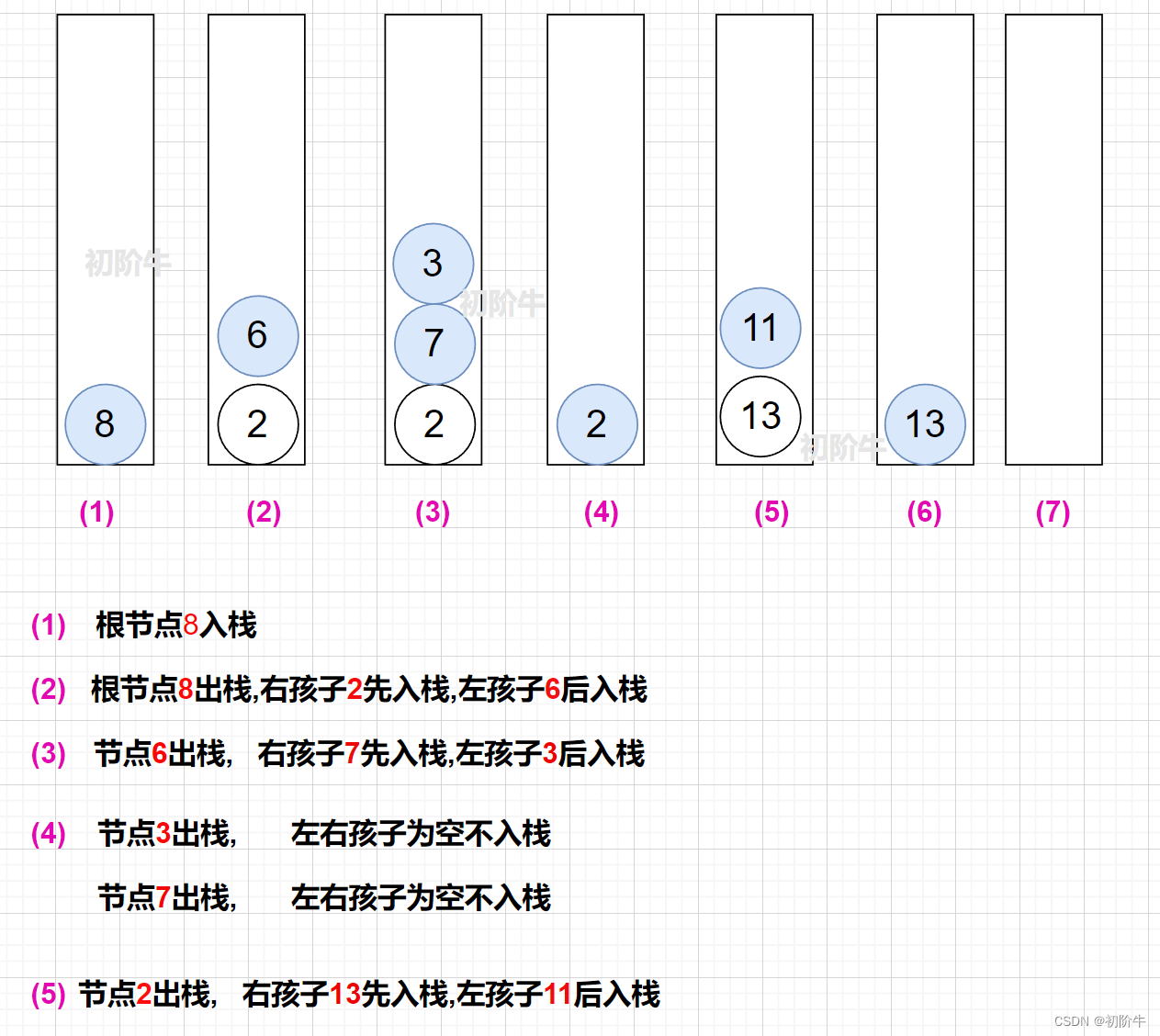 (图片为博主:"初阶牛"原创,未经允许,不得复制)
(图片为博主:"初阶牛"原创,未经允许,不得复制)
结果:

🍔非递归代码实现1:
class Solution {public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> s1;vector<int> v1;s1.push(root);//根节点先入栈while (!s1.empty()) { //当栈为空时,结束TreeNode* top = s1.top();if(top==nullptr)break;v1.push_back(top->val); //出栈前,先将栈顶元素存入vector//栈顶元素出栈s1.pop();//栈顶元素的右左子树入栈if (top->right)s1.push(top->right);if (top->left)s1.push(top->left);}return v1;}};
方法二、思路分析
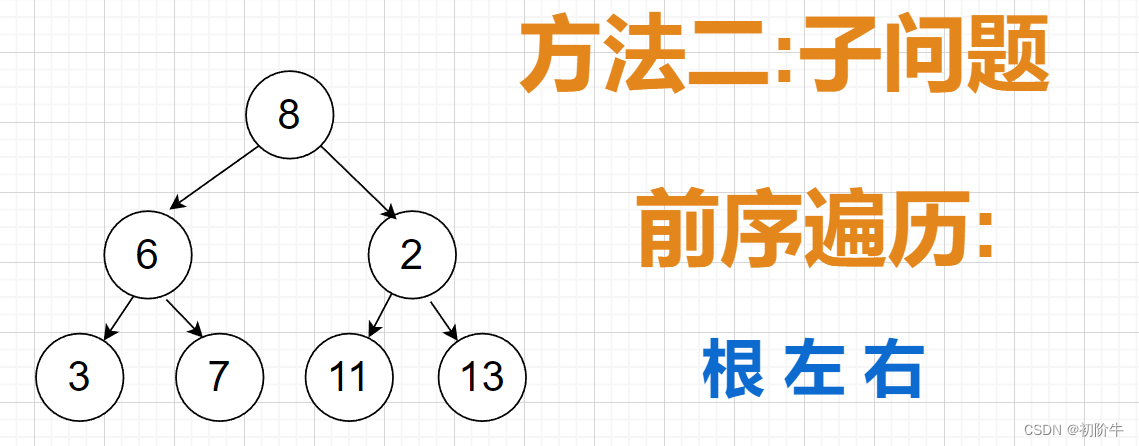
- 左路节点一边存入vector,一边入栈.
- 栈顶元素出栈,如果栈顶元素有右子树,则将右子树转化为子问题,和步骤1一样.
注意循环的结束条件.
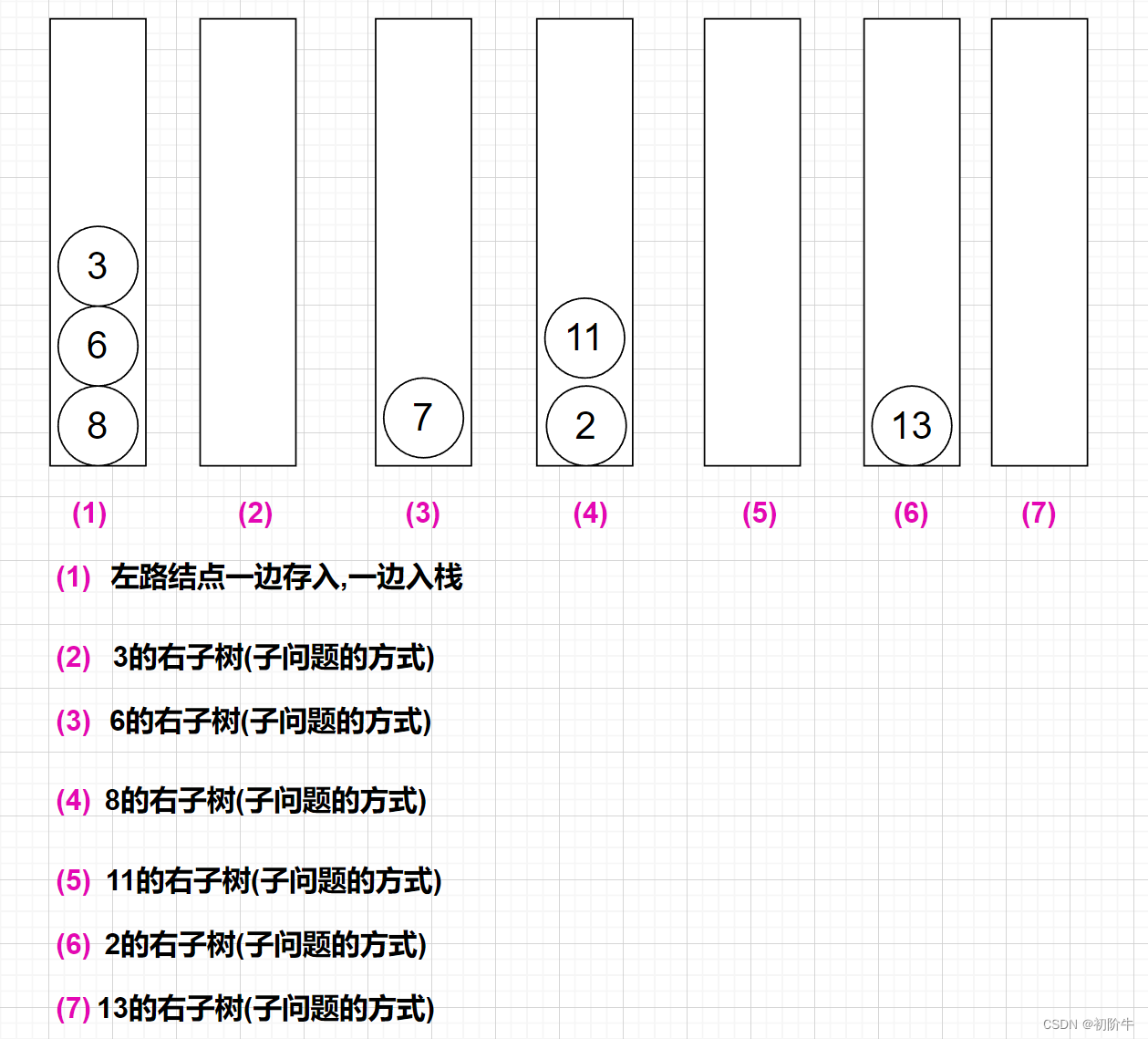 (图片为博主:"初阶牛"原创,未经允许,不得复制)
(图片为博主:"初阶牛"原创,未经允许,不得复制)
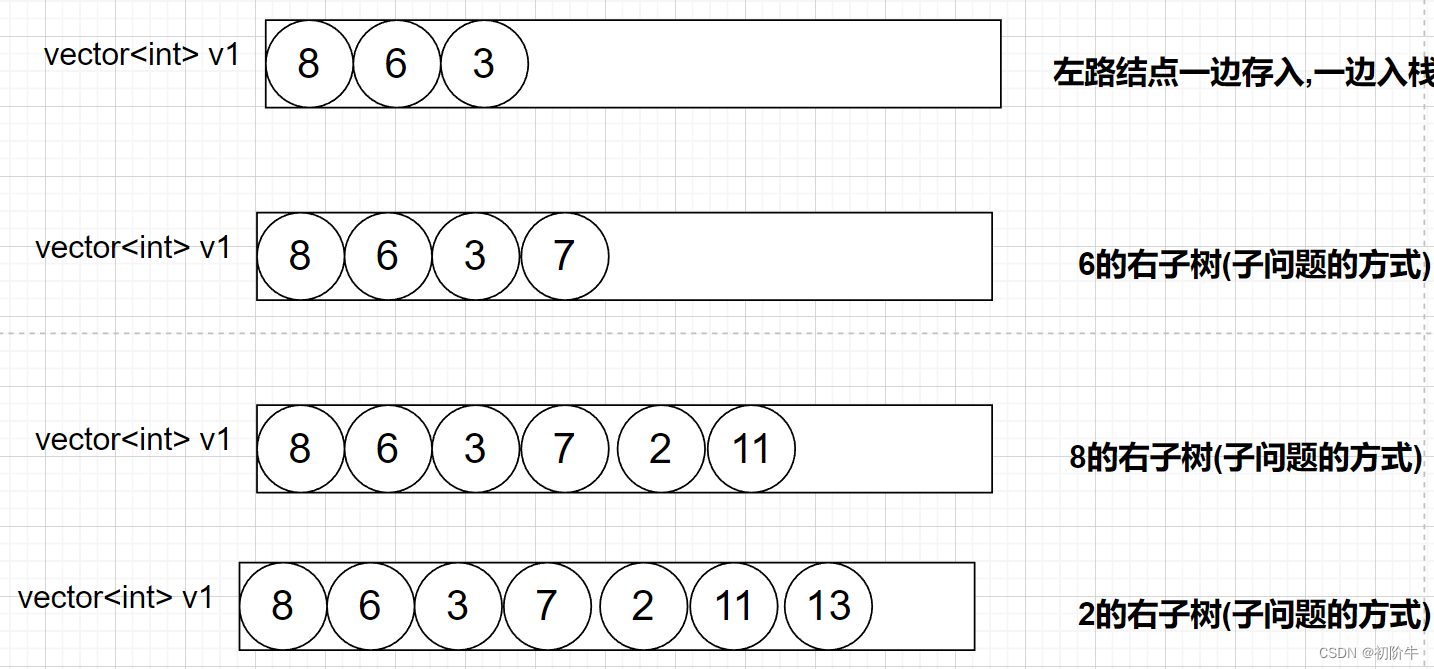
(图片为博主:"初阶牛"原创,未经允许,不得复制)
🍉非递归实现2:
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> v1;stack<TreeNode*> s1;TreeNode* cur=root;while(cur || !s1.empty()){//将左路节点全部存入栈while(cur){v1.push_back(cur->val);s1.push(cur);cur=cur->left;}//栈顶元素出栈TreeNode*top=s1.top();s1.pop();//如果栈顶元素的右子树存在,则转化为子问题解决.if(top->right)cur=top->right; //关键语句,通过让cur等于栈顶元素的右子树.}return v1;}
};
二、非递归实现"中序遍历"
题目链接:传送门
题目描述:
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
补充知识:
二叉树的中序遍历指的是按照从小到大的顺序,依次访问二叉树中的所有节点。即先访问左子树,再访问根节点,最后访问右子树。
中序遍历算法如下:
- 如果当前节点的左子树非空,则递归遍历左子树。
- 访问当前节点。
- 如果当前节点的右子树非空,则递归遍历右子树。
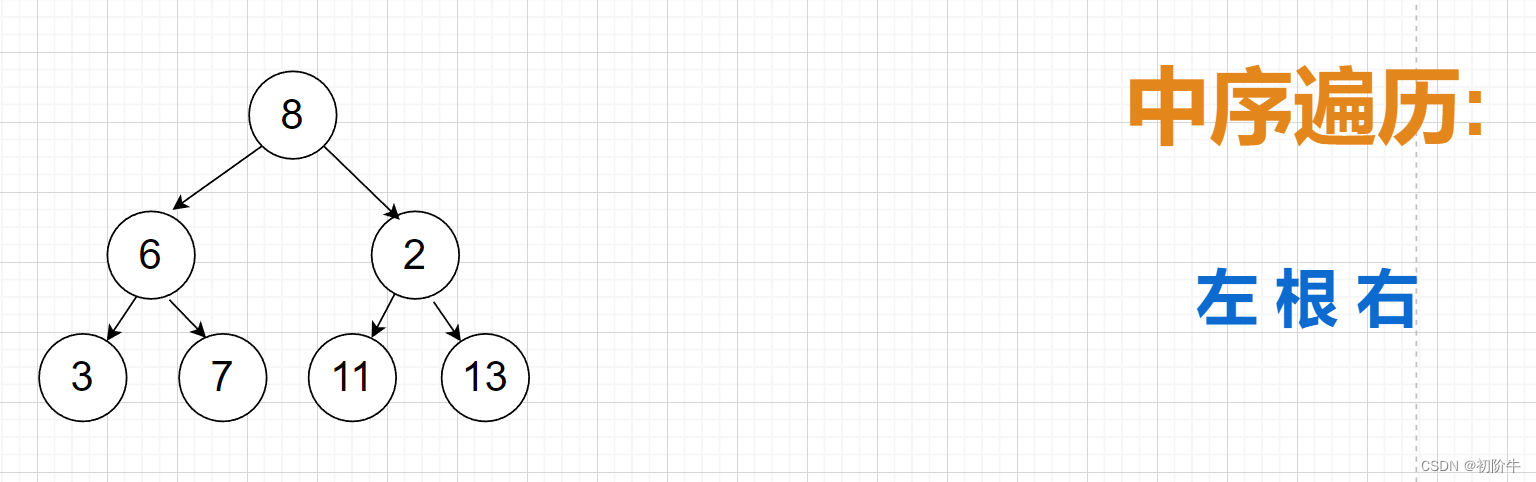
思路分析:
有了前面的前序遍历的思想,对于中序遍历,需要注意的是存入容器(这里是vector)的时机.
- 左路节点依次入栈.(与前序对比:此时入栈并没有入容器.)
- 栈顶元素入容器,栈顶元素出栈,栈顶元素的右子树子问题解决.
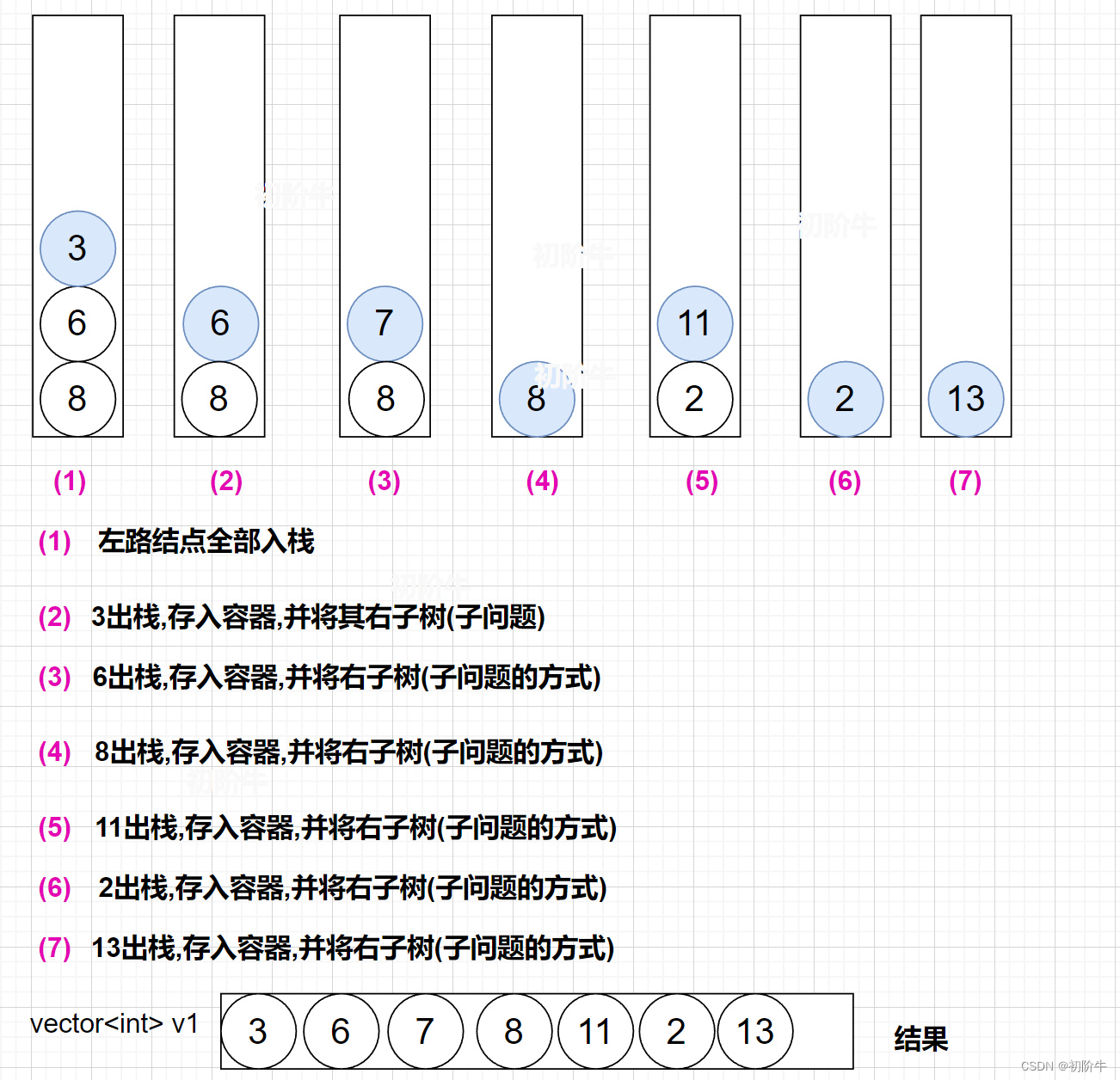
(图片为博主:"初阶牛"原创,未经允许,不得复制)
🔑非递归代码实现:
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {stack<TreeNode*> s1;vector<int> v1;TreeNode* cur=root;while(cur||!s1.empty()){//沿着左子树一直入节点while(cur){s1.push(cur);cur=cur->left;}TreeNode* top = s1.top();if(top==nullptr)break;v1.push_back(top->val);//栈顶元素出栈s1.pop();//右子树 以子问题的方式解决if(top->right)cur=top->right;}return v1;}
};
三、非递归实现"后序遍历"
题目链接:传送门
题目描述:
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
二叉树的后序遍历指的是先访问左右子树,最后访问根节点的顺序遍历。即先遍历左子树,再遍历右子树,最后访问根节点。
后序遍历算法如下:
- 如果当前节点的左子树非空,则递归遍历左子树。
- 如果当前节点的右子树非空,则递归遍历右子树。
- 访问当前节点。
思路分析
对于后序遍历,同样注意存入容器的时机,应当是左子树和右子树都访问完毕,才能够访问根节点.
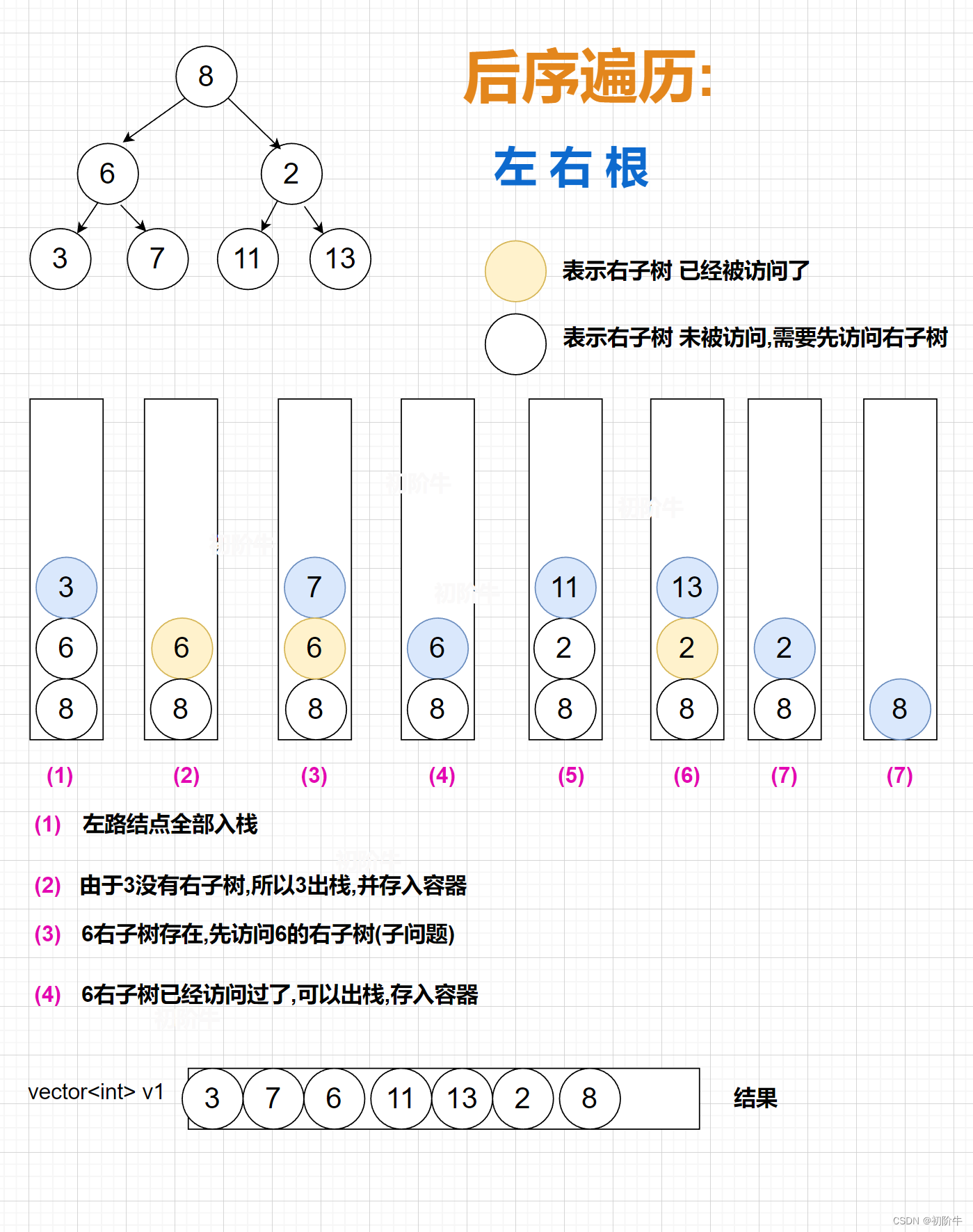
注意点:
(1)访问结点之前,需要先判断右子树是否已经被访问.
如何判断根节点的右子树已经有没有访问?
答案: 上一个存入的结点是自己右子树,则右子树已经被访问.
上一个结点不是自己的右子树,则右子树未被访问.
示例:
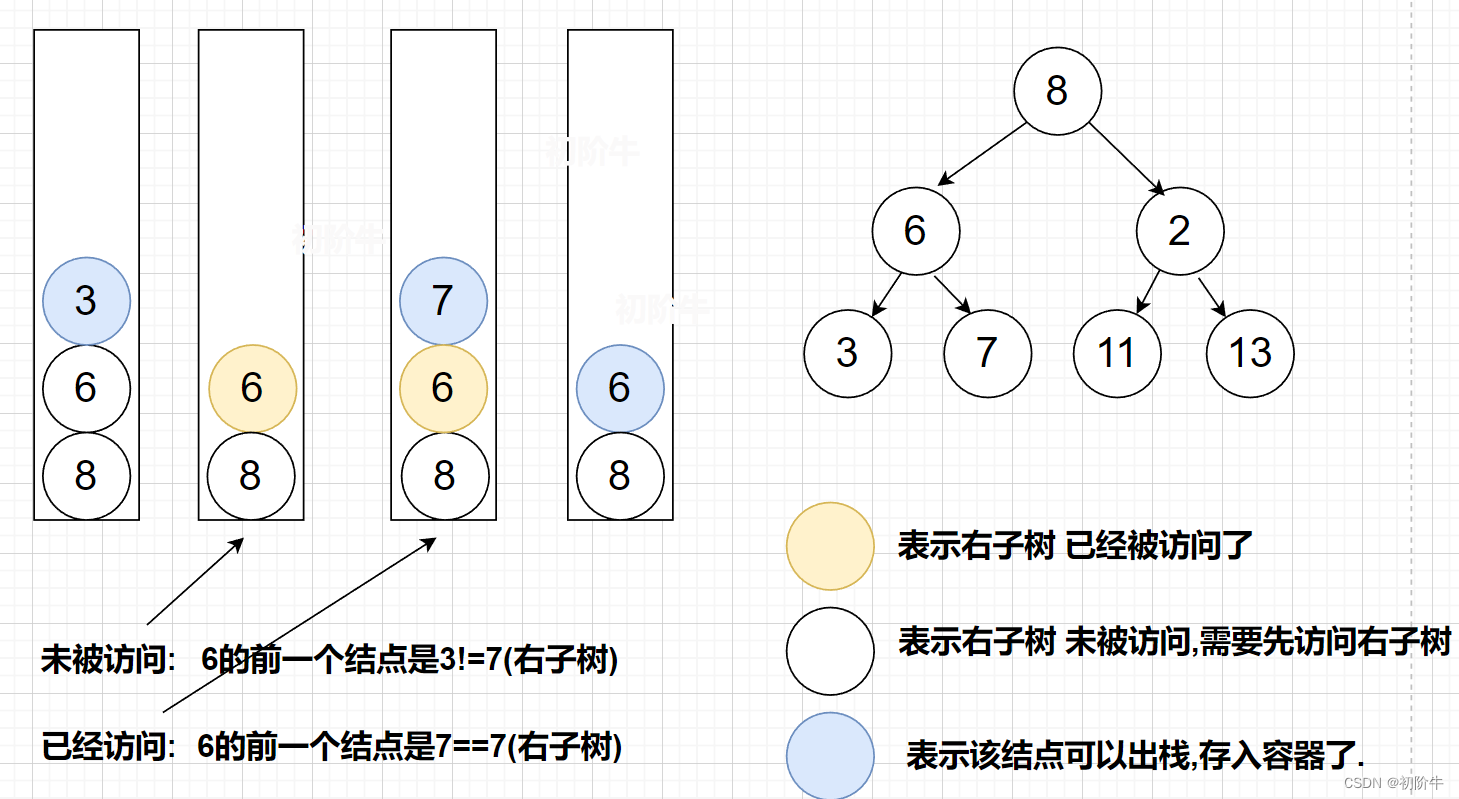
💗非递归代码实现:
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> s1;vector<int> v1;TreeNode* prv = nullptr;TreeNode* cur = root;while (cur || !s1.empty()) {//沿着左子树一直入节点while (cur) {s1.push(cur);cur = cur->left;}TreeNode* top = s1.top();if (top == nullptr)break;//右子树 以子问题的方式解决if (prv!=top->right && top->right) {cur = top->right;continue;} prv=top;v1.push_back(top->val);//栈顶元素出栈s1.pop();}return v1;}
};
相关文章:

二叉树的前 中 后序的非递归实现(图文详解)
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻强烈推荐优质专栏: 🍔🍟🌯C的世界(持续更新中) 🐻推荐专栏1: 🍔🍟🌯C语言初阶 🐻推荐专栏2: 🍔…...
.NET验收
验收通用模板: 1.该资料计划看几天? 实际看了几天? 计划7天,实际看了9天 2.多少天一篇总结?将总结列出来。 一周总结一篇。 博客地址:3.这个资料相较于之前资料共同的内容是什么? 不同的(需要强化学习)…...
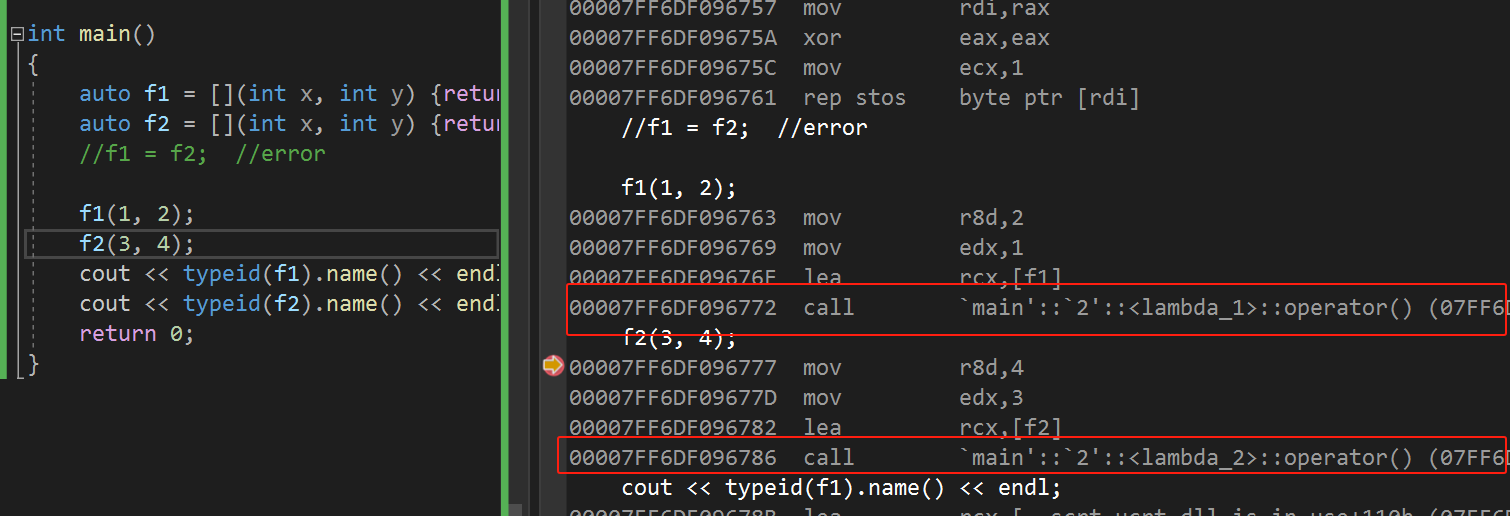
C++11——lambda表达式
文章目录 1. C98对自定义类型的排序2. lambda表达式语法2.1 捕捉列表 3. lambda底层原理 1. C98对自定义类型的排序 在C98中,想要对自定义类型就行排序,我们得自己写仿函数来表明我们相对哪一项进行排序 struct Student {Student(string name, long id…...

美国加密货币交易和借贷平台Membrane Labs完成2000万美元融资
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,总部位于美国纽约的加密货币交易和借贷平台Membrane Labs今日宣布已完成2000万美元A轮融资。 参与本轮融资的投资机构包括:Brevan Howard Digital、Point72 Ventures、Jane Street Cap…...

8-k8s-污点与容忍
文章目录 一、概念二、相关操作三、实操污点NoSchedule四、实操污点NoExecute五、实操容忍 一、概念 污点与容忍 污点taints定义在节点之上的键值型属性数据。当节点被标记为有污点,那么意味着不允许pod调度到该节点。 容忍tolerations是定义在 Pod对象上的键值型属…...
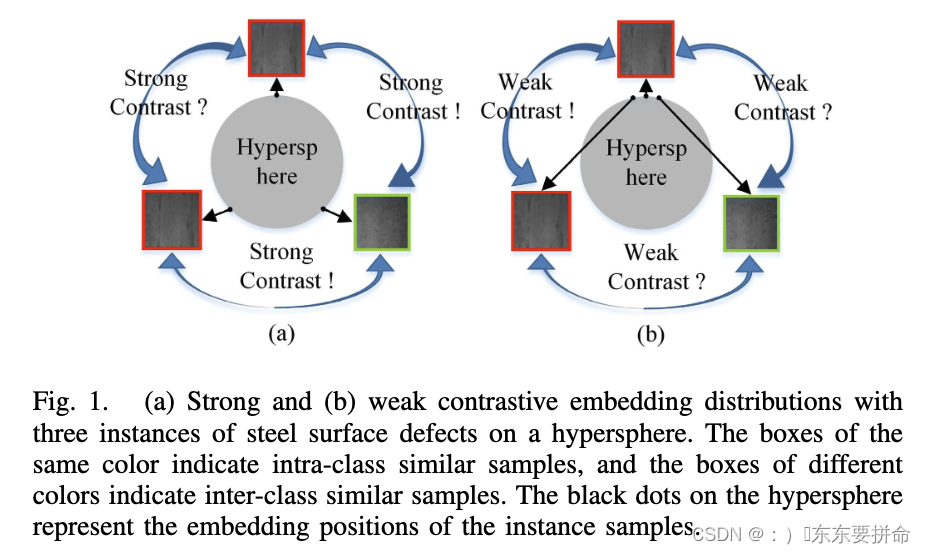
钢铁异常分类140篇Trans 学习笔记 小陈读paper
钢铁异常分类 对比学习 比较好用 1.首先,为每个实例生成一对样本, 来自同一实例的样本被认为是正例, 来自不同实例的样本被认为是负例。 2.其次,这些样本被馈送到编码器以获得嵌入。 3.在对比损失[16]的影响下, …...
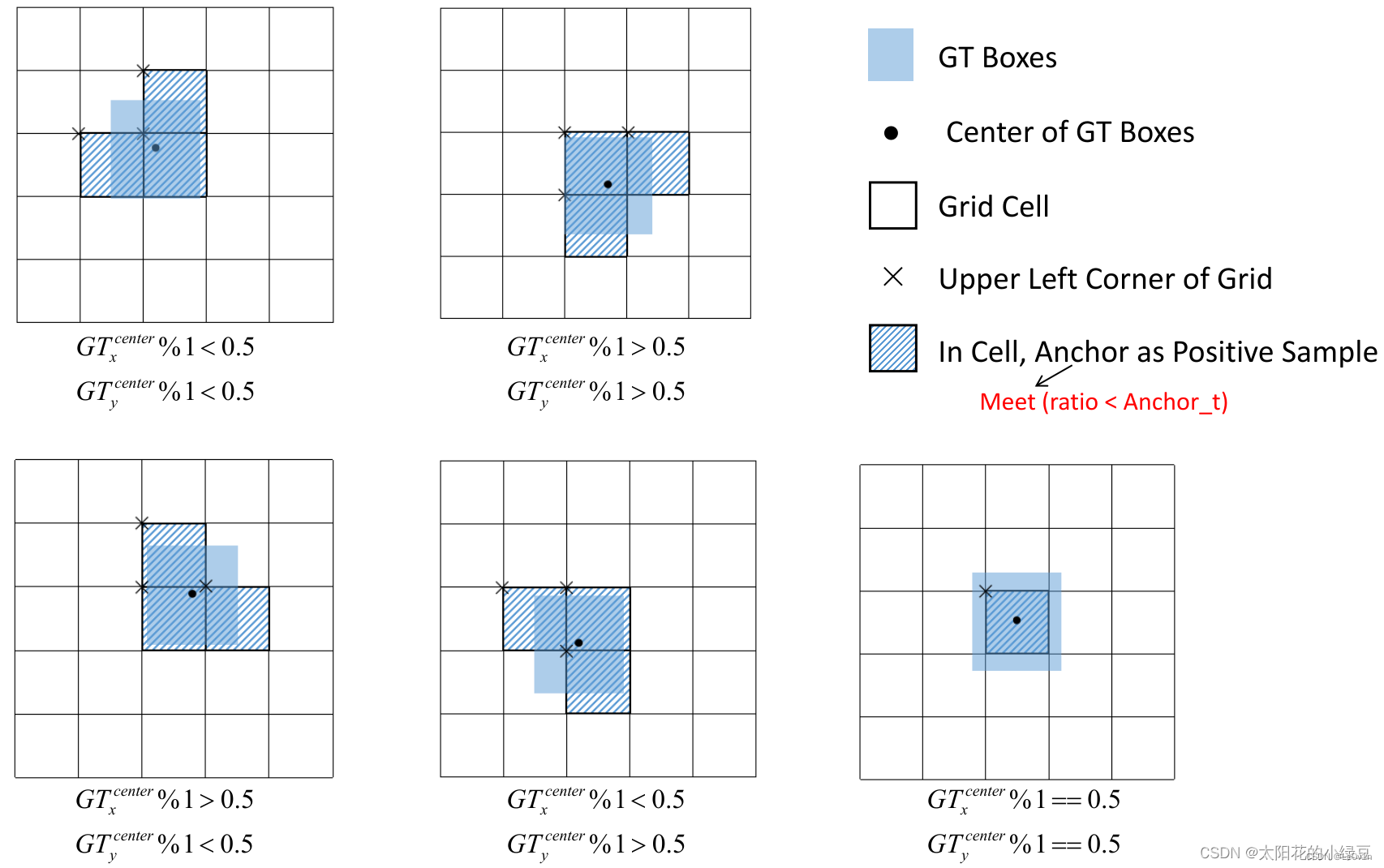
YOLOv5-理论部分
YOLOv5 作者: Ultralytics 论文源码: https://github.com/ultralytics/yolov5 Ultralytics:“超视觉技术” / “超视觉系统” 0. 引言 “YOLOv5 🚀 是世界上备受喜爱的视觉人工智能,代表了 Ultralytics 对未来视觉人工智能方法的开源研究&a…...

蓝桥等考C++组别一级004
第一部分:选择题 1、C L1(15分) 下列是编程语言的一项是( )。 A. C B. Word C. Excel D. PowerPoint 正确答案: A 2、C L1(15分) 仔细阅读以下程序代码,其中有…...
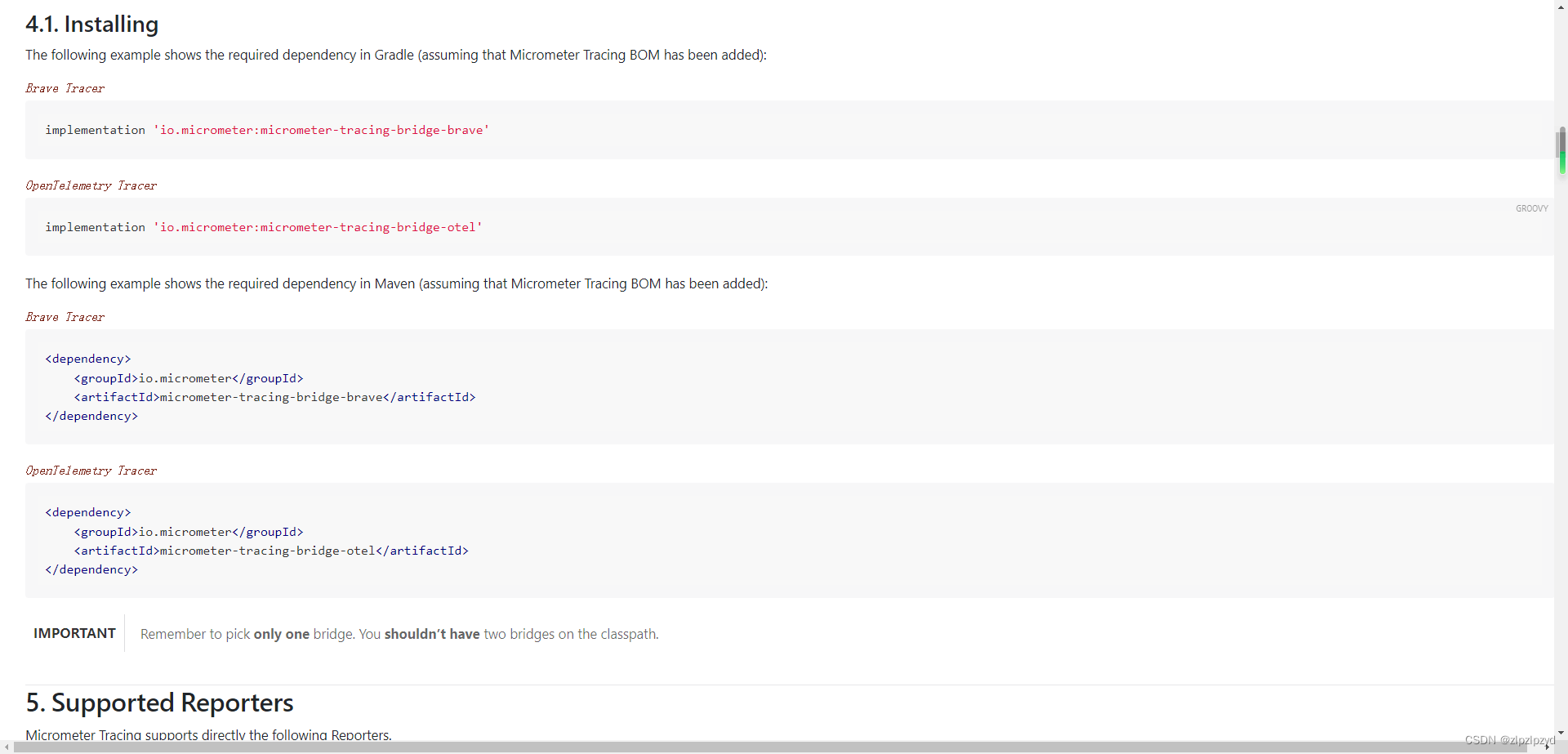
分布式服务的链路跟踪 Sleuth Micrometer zipkin OpenTelemetry
由来 在分布式应用开发过程中,一个请求会调用多个应用,会有那种需要知道各个应用之间耗时的想法,这样可以知道一个调用的总时长以及各个组件之间的处理耗时,后面方便定位问题。 理论依据 起源于 google dapper 论文 https://re…...

CUDA学习笔记4——自定义设备函数
自定义设备函数 核函数:__global__修饰;在设备中执行;设备函数:__device__修饰;在设备中执行;只能被核函数或其他设备函数调用;主机函数:__host__修饰(可省略࿰…...
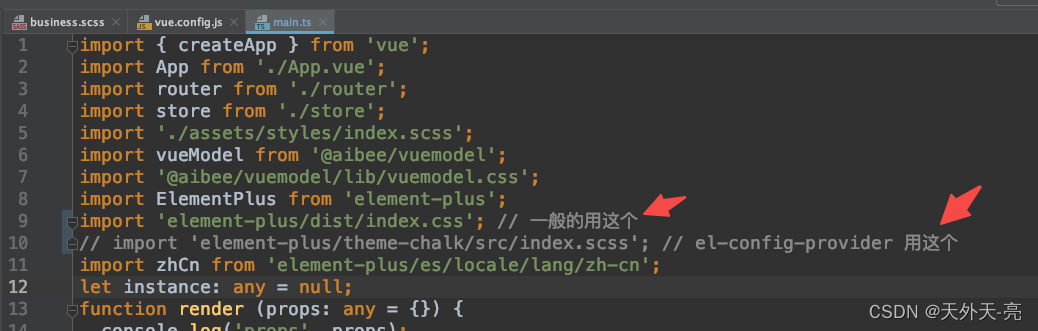
微前端四:qiankun在开发中遇到的问题
在qiankun开发中会遇到很多问题,上一篇微前端三:qiankun 协作开发和上线部署其实也是在解决一些经常遇到的问题,下面的两点也算是比较经典的了 1、子应用图片路径问题 2、基座是Vue2.0 element ui 配合 子应用 Vue3.0 element plus 导致的样…...

Android DisplayPolicy增加一些动作,打开后台接口
Android DisplayPolicy增加一些动作,打开后台接口 前言一、了解android全局滑动事件的拦截二、修改1.DisplayPolicy.java修改 前言 一些后台接口 界面之类的不方便打开,但是测试需要用到,这里就添加一个10秒内上拉6下,打开一个后…...
基于Linux安装Hive
Hive安装包下载地址 Index of /dist/hive 上传解压 [rootmaster opt]# cd /usr/local/ [rootmaster local]# tar -zxvf /opt/apache-hive-3.1.2-bin.tar.gz重命名及更改权限 mv apache-hive-3.1.2-bin hivechown -R hadoop:hadoop hive配置环境变量 #编辑配置 vi /etc/pro…...

FPGA 图像缩放 1G/2.5G Ethernet PCS/PMA or SGMII实现 UDP 网络视频传输,提供工程和QT上位机源码加技术支持
目录 1、前言版本更新说明免责声明 2、相关方案推荐UDP视频传输--无缩放FPGA图像缩放方案我这里已有的以太网方案 3、设计思路框架视频源选择ADV7611 解码芯片配置及采集动态彩条跨时钟FIFO图像缩放模块详解设计框图代码框图2种插值算法的整合与选择 UDP协议栈UDP视频数据组包U…...

重复控制逆变器的仿真分析研究
摘 要 本次设计主要以重复控制逆变器控制系统设计应用作为研究背景,运用MATLAB/Simulink仿真工具搭建相应的仿真模型。重复控制逆变器控制系统拥有很好的动态特性,运行稳定性高、调速的范围较大,性能可靠等,在实际生产制造中被广…...

WuThreat身份安全云-TVD每日漏洞情报-2023-10-18
漏洞名称:致远 OA XML 外部实体注入漏洞 漏洞级别:高危 漏洞编号:NULL 相关涉及:V5/G6 V6.0及以上全系列版本 漏洞状态:POC 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-26027 漏洞名称:XNSOFT NCONVERT 图像文件缓冲区溢出 漏洞级别:中危 漏洞编号:CVE-…...

开启机器人学新时代,《机器人学建模、规划与控制》完美诠释未来
机器人学是未来发展的热点领域之一,而在这个领域中,建模、规划与控制则是必不可少的基础技术。今天作者要向大家推荐一本机器人学领域的经典教材——《机器人学建模、规划与控制》。 这本书由西安交通大学出版社出版,作者是机器人学专业的鼎…...

C#根据ip获取地理位置信息的方法,史上最全
商业收费 百度地图高德地图腾讯地图纯真IP 开源免费 纯真ip免费版 以前可以直接下载,现在获取ip数据库的方式改变了,自行官网查看把,个人或者学术研究,商用追责,商业用途慎用 using System.Collections.Generic; us…...

Git问题汇总
1.取消全局代理 一般报错Failed to connect to github.com port 443 after 21089 ms: Couldn’t connect to server 取消全局代理: git config --global --unset http.proxygit config --global --unset https.proxy#或者 git config --global http.proxy http://…...
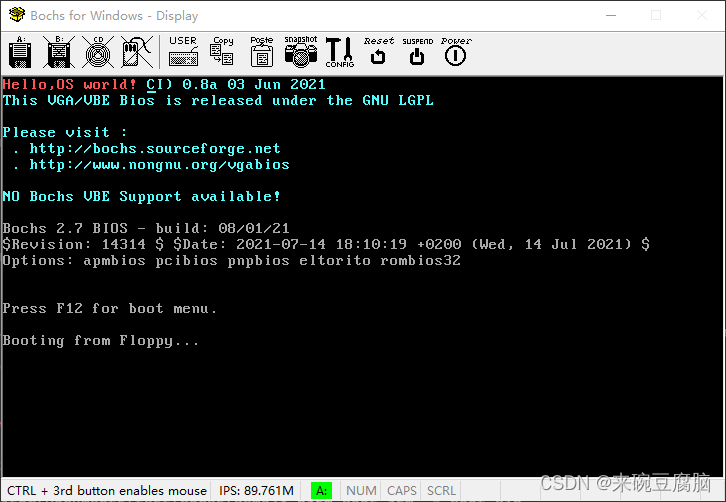
【linux 0.11 学习记录】一、环境配置,用Bochs输出hello world
想学习linux,又不知道从哪里下手,体系太大,哪块内容都很多,无奈下选择了linux0.11作为入口,本系列将是学习笔记,希望能坚持下去吧 环境配置 这里使用win10bochs2.7 安装bochs 官网:https://b…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
