【C语言经典例题】打印菱形
目录
一、题目要求
二、解题思路
上半部分三角形
打印空格
打印星号*
下半部分三角形
打印空格
打印星号*
三、完整代码
代码
运行截图:
一、题目要求
输入一个整数n(n为奇数),n为菱形的高,打印出该菱形
例:
输入:13
输出:

二、解题思路
这里我就拿上面输入 13 的例子来解释哈
先把菱形看成是上下两个三角形,然后分别打印即可;
又由于把多出来那一行放到上面的三角形去,更容易观察出结论,所以我就把最中间那一行归到上面的三角形去了,也就是这样子:
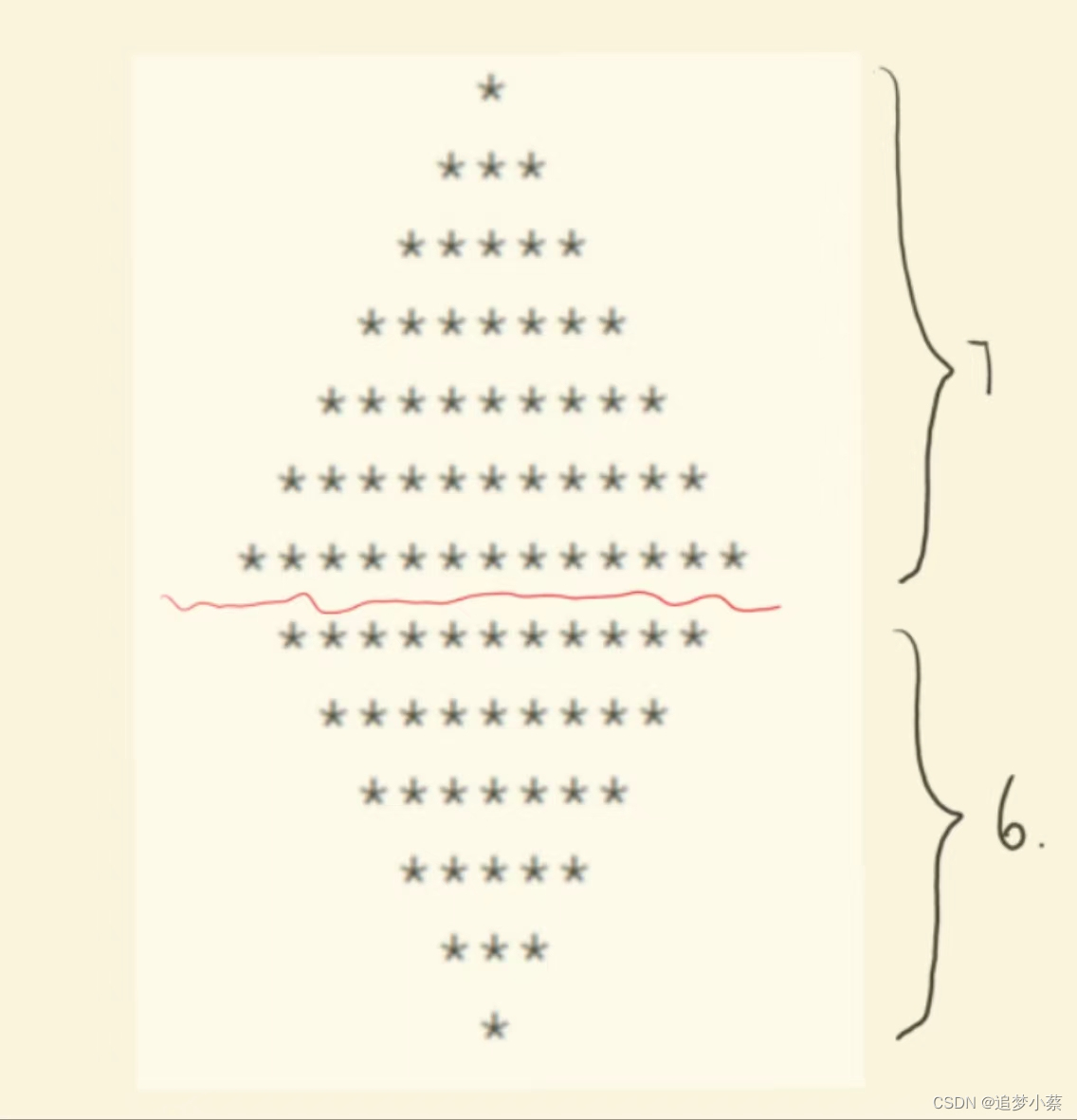
由此我们可以看出,上面的三角形,高为 n/2+1 ,而下面的三角形则是 n/2
我们先来看上面的三角形如何打印:
上半部分三角形
打印三角形分为 打印空格 和 打印星号*
打印空格
我们可以看到,星号* 能打印在中间,前面一定有空格把他顶过去的。
也就是这样子:

那么要打印多少个空格呢?
请看下面的分析:

由此我们就可以推算出空格数目的公式:
空格数= (n+1)/2 - 行数(i)
打印星号*
我们直接来看下星号个数的分析:

可以看出,
在上半部分的三角形中,星号数 = 行数 * 2 - 1
下半部分三角形
老样子,打印三角形还是分为 打印空格 和 打印星号
打印空格
在下半部分,我把行数重新从零开始计算,数字小点会更容易找规律
请看下面的图解:

不难看出,在下半部分的三角形中
空格数 = 行数(i)
打印星号*
老规矩,直接上思路图解:

由图我们可以看出,
在下半部分的三角形中,星号数 = n - 2 * 空格数
至此,上下两个三角形的规律已全部找出,接下来只要打印出来就好啦
三、完整代码
请看完整代码:
代码
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>int main()
{int i, j, k, n;printf("请输入菱形的高(必须为奇数):");while(~scanf("%d", &n)) {if (n % 2 == 0){printf("输入错误,请重新输入\n");}elsebreak;}for (i = 1; i <= (n / 2) + 1; i++) //i为行数{for (j = 1; j <= (n + 1) / 2 - i; j++)printf(" ");for (k = 1; k <= 2 * i - 1; k++)printf("*");printf("\n");}for (i = 1; i <= n / 2; i++) //i为行数{for (j = 1; j <= i; j++)printf(" ");for (k = 1; k <= n - 2 * i; k++)printf("*");printf("\n");}return 0;
}运行截图:

以上就是本篇博客的全部内容啦,如有不足之处,还请各位指出,期待能和各位一起进步!
相关文章:

【C语言经典例题】打印菱形
目录 一、题目要求 二、解题思路 上半部分三角形 打印空格 打印星号* 下半部分三角形 打印空格 打印星号* 三、完整代码 代码 运行截图: 一、题目要求 输入一个整数n(n为奇数),n为菱形的高,打印出该菱形 例&a…...
easyExcel与poi版本不兼容导致的后台报错问题
1、背景:最新接手公司系统excel导入解析模块,点击批量导入,后台报错如下 com.alibaba.excel.exception.ExcelAnalysisException: java.lang.NoClassDefFoundError: org/apache/poi/poifs/filesystem/FileMagicat com.alibaba.excel.analysis.…...
Fiddler报文分析-断点应用、模拟网络限速-HTTPS的 拦截
目录 一、报文分析 Statistics 请求性能数据 检查器(Inspectors) 自定义响应(AutoResponder) Composer Composer的功能就是用来创建HTTP Request然后发送请求。 允许自定义请求发送到服务器,即可以手动创建一个新…...
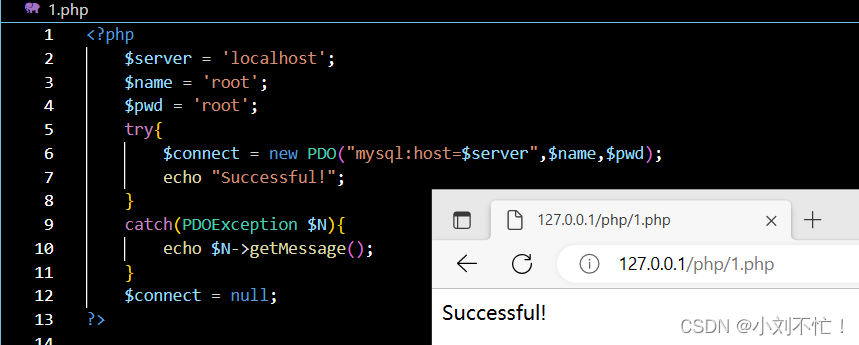
PHP基础(3)
PHP基础表单提交文件处理PHP连接数据库异常抛出表单提交 PHP通过全局变量 $_GET和 $_POST来收集表单数据。 接下来改用post方式进行提交,再次查看是否隐藏了提交的内容: 发现提交的信息已经不在链接之中进行显示了。 GET与POST区别在于一个会在连接…...
跳槽进字节跳动了,面试真的很简单
前言: 最近金三银四跳槽季,相信很多小伙伴都在面试找工作, 怎样才能拿到大厂的offer,没有掌握绝对的技术,那么就要不断的学习 如何拿下阿里等大厂的offer的呢,今天分享一个秘密武器,资深测试工程师整理的…...

【SpringBoot9】HandlerInterceptor拦截器的使用 ——防重复提交
看本篇博客前应当先看完前面三篇,这一篇是基于前面三篇的知识点的整合。所以很多重复的代码这里就不写出了 后台通过拦截器和redis实现防重复提交,避免因为网络原因导致多次请求同时进入业务系统,导致数据错乱,也可以防止对外暴露…...
之域控安全和跨域攻击-约束性委派攻击)
内网渗透(五十八)之域控安全和跨域攻击-约束性委派攻击
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Linux僵尸进程理解作业详解
1 下面有关孤儿进程和僵尸进程的描述,说法错误的是? A.孤儿进程:一个父进程退出,而它的一个或多个子进程还在运行,那么那些子进程将成为孤儿进程。 B.僵尸进程:一个进程使用fork创建子进程,如果…...
)
每日一题——L1-078 吉老师的回归(15)
L1-078 吉老师的回归 曾经在天梯赛大杀四方的吉老师决定回归天梯赛赛场啦! 为了简化题目,我们不妨假设天梯赛的每道题目可以用一个不超过 500 的、只包括可打印符号的字符串描述出来,如:Problem A: Print "Hello world!&qu…...

ESP32设备驱动-DS1264数字温度传感器驱动
DS1264数字温度传感器驱动 1、DS1264介绍 DS1624 由两个独立的功能单元组成:一个 256 字节非易失性 E2 存储器和一个直接数字温度传感器。 非易失性存储器由 256 字节的 E2 存储器组成。 该存储器可用于存储用户希望的任何类型的信息。 这些内存位置通过 2 线串行总线访问。…...
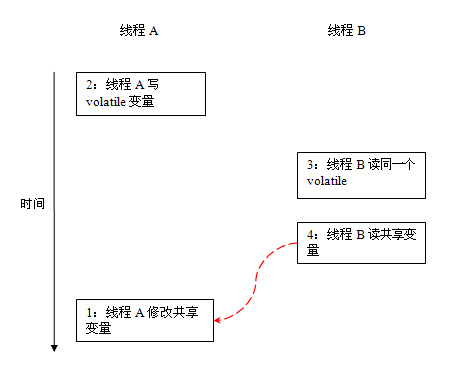
8000+字,就说一个字Volatile
简介 volatile是Java提供的一种轻量级的同步机制。Java 语言包含两种内在的同步机制:同步块(或方法)和 volatile 变量,相比于synchronized(synchronized通常称为重量级锁),volatile更轻量级&…...

MySQL的函数
Java知识点总结:想看的可以从这里进入 目录3.3、MySQL的函数3.3.1、字符串函数3.3.2、数学函数3.3.3、聚合函数3.3.4、日期函数3.3.5、条件判断函数3.3.6、系統信息函数3.3.7、其他函数3.3、MySQL的函数 MySQL提供了丰富的内置函数,这些函数使得数据的维…...

python排序算法
排序是指以特定格式排列数据。 排序算法指定按特定顺序排列数据的方式。 最常见的排序是数字或字典顺序。 排序的重要性在于,如果数据是以分类方式存储,数据搜索可以优化到非常高的水平。 排序也用于以更易读的格式表示数据。 下面来看看python中实现的5…...

【C++入门第二期】引用 和 内联函数 的使用方法及注意事项
前言引用的概念初识引用区分引用和取地址引用与对象的关系引用的特性引用的使用场景传值和引用性能比较引用和指针的区别内联函数内联函数的概念内联函数的特性前言 本文主要学习的是引用 及 内联含函数,其中的引用在实际使用中会异常舒适。 引用的概念 概念&…...
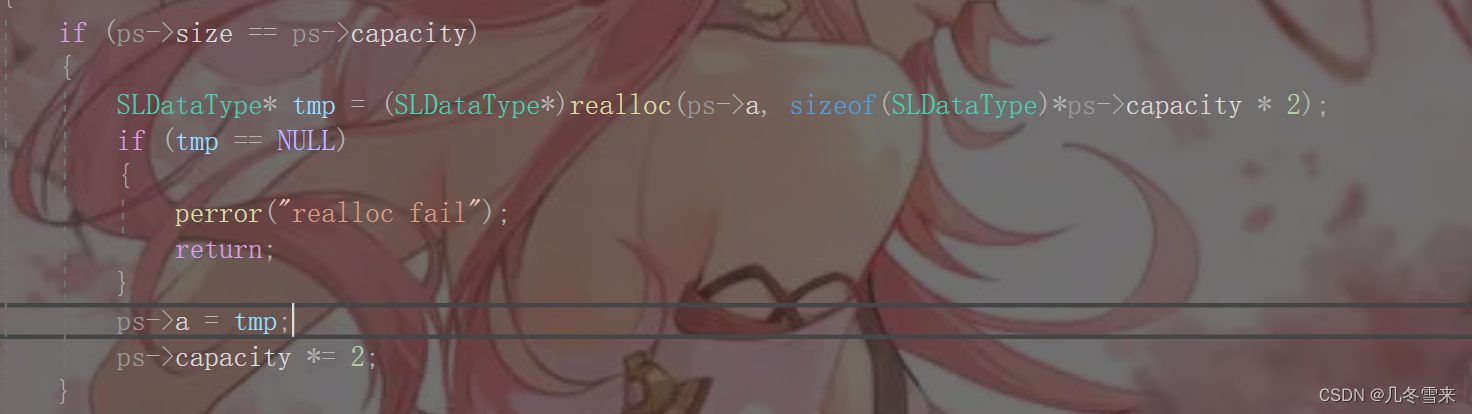
数据结构——顺序表讲解
作者:几冬雪来 时间:2023年2月25日 内容:数据结构顺序表内容讲解 目录 前言: 顺序表: 1.线性表: 2.什么是顺序表: 3.顺序表的概念和构成: 4.顺序表的书写: 1…...
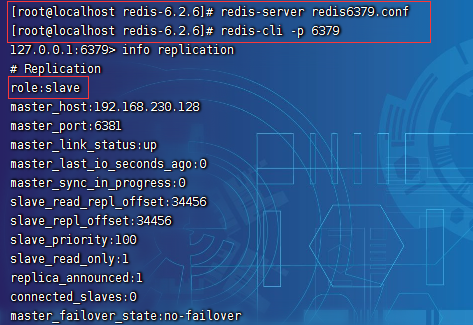
Redis 主从复制-服务器搭建【薪火相传/哨兵模式】
Redis 安装参考文章:Centos7 安装并启动 Redis-6.2.6 注意:本篇文章操作,不能在 静态IP地址 下操作,必须是 动态IP地址,否则最后主从服务器配置不成功! 管道符查看所有redis进程:ps -ef|grep re…...
分组查询)
数据库|(五)分组查询
(五)分组查询1. 介绍2. 语法3. 简单分组函数2. 添加筛选条件3. 添加复杂的筛选条件4. 分组查询特点5. 按表达式或函数分组6. 按多个字段分组7. 分组查询添加排序1. 介绍 引入:查询每个部门的平均工资 -- 以前写法:求的是总平均工…...

Orin安装ssh、vnc教程
文章目录一:ssh远程终端的配置PC的配置MobaXterm的下载二:VNC Viewer远程图形界面终端配置:PC配置:一:ssh远程 终端的配置 1.ifconfig查看终端ip地址 其中的eth是网口,我们需要看的是wlan0下的inet&#…...
Allegro如何快速删除孤立铜皮操作指导
Allegro如何快速删除孤立铜皮操作指导 在做PCB设计的时候,铺铜是常用的设计方式,在PCB设计完成之后,需要删除PCB上孤立的铜皮,即铜皮有网络但是却没有任何连接 如下图 通过Status报表也可以看到Isolated shapes 如何快速地删除孤立铜皮,具体操作如下 点击Shape...

从单管单色到单管RGB,这项MicroLED工艺不可忽视
微显示技术商Porotech,在CES 2023期间展示了最新的MicroLED显示模组。近期,AR/VR光学领域的知名博主Karl Guttag深度分析了该公司的微显示技术,并指出Porotech带来了他见过最有趣的MicroLED技术。Guttag表示:Porotech是本届CES上给…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
