python排序算法
排序是指以特定格式排列数据。 排序算法指定按特定顺序排列数据的方式。 最常见的排序是数字或字典顺序。
排序的重要性在于,如果数据是以分类方式存储,数据搜索可以优化到非常高的水平。 排序也用于以更易读的格式表示数据。 下面来看看python中实现的5种排序方式。
- 冒泡排序
- 合并排序
- 插入排序
- 希尔排序
- 选择排序
冒泡排序
它是一种基于比较的算法,其中每对相邻元素进行比较,如果元素不合适,元素将进行交换。
def bubblesort(list):# Swap the elements to arrange in orderfor iter_num in range(len(list)-1,0,-1):for idx in range(iter_num):if list[idx]>list[idx+1]:temp = list[idx]list[idx] = list[idx+1]list[idx+1] = templist = [19,2,31,45,6,11,121,27]
bubblesort(list)
print(list)
执行上面示例代码,得到以下结果 -
[2, 6, 11, 19, 27, 31, 45, 121]
合并排序
合并排序首先将数组分成相等的一半,然后以排序的方式组合它们。参考以下代码实现 -
def merge_sort(unsorted_list):if len(unsorted_list) <= 1:return unsorted_list
# Find the middle point and devide itmiddle = len(unsorted_list) // 2left_list = unsorted_list[:middle]right_list = unsorted_list[middle:]left_list = merge_sort(left_list)right_list = merge_sort(right_list)return list(merge(left_list, right_list))# Merge the sorted halvesdef merge(left_half,right_half):res = []while len(left_half) != 0 and len(right_half) != 0:if left_half[0] < right_half[0]:res.append(left_half[0])left_half.remove(left_half[0])else:res.append(right_half[0])right_half.remove(right_half[0])if len(left_half) == 0:res = res + right_halfelse:res = res + left_halfreturn resunsorted_list = [64, 34, 25, 12, 22, 11, 90]print(merge_sort(unsorted_list))执行上面示例代码,得到以下结果 -
[11, 12, 22, 25, 34, 64, 90]
插入排序
插入排序包括为排序列表中的给定元素找到正确的位置。 所以在开始时比较前两个元素并通过比较来对它们进行排序。 然后选取第三个元素,并在前两个排序元素中找到它的正确位置。 通过这种方式,逐渐将更多元素添加到已排序的列表中,并将它们置于适当的位置。
参考下面代码的实现 -
def insertion_sort(InputList):for i in range(1, len(InputList)):j = i-1nxt_element = InputList[i]
# Compare the current element with next onewhile (InputList[j] > nxt_element) and (j >= 0):InputList[j+1] = InputList[j]j=j-1InputList[j+1] = nxt_elementlist = [19,2,31,45,30,11,121,27]
insertion_sort(list)
print(list)
执行上面示例代码,得到以下结果 -
[2, 11, 19, 27, 30, 31, 45, 121]
希尔排序
希尔排序涉及排序远离其他的元素。对给定列表的大型子列表进行排序,并继续缩小列表的大小,直到所有元素都被排序。 下面的程序通过将其等于列表大小的一半来找到间隙,然后开始对其中的所有元素进行排序。 然后不断重置差距,直到整个列表被排序。
def shellSort(input_list):gap = len(input_list) / 2while gap > 0:for i in range(gap, len(input_list)):temp = input_list[i]j = i
# Sort the sub list for this gapwhile j >= gap and input_list[j - gap] > temp:input_list[j] = input_list[j - gap]j = j-gapinput_list[j] = temp# Reduce the gap for the next elementgap = gap/2list = [19,2,31,45,30,11,121,27]shellSort(list)
print(list)
执行上面示例代码,得到以下结果 -
[2, 11, 19, 27, 30, 31, 45, 121]
选择排序
在选择排序中,首先查找给定列表中的最小值并将其移至排序列表。 然后为未排序列表中的每个剩余元素重复该过程。 输入排序列表的下一个元素将与现有元素进行比较并放置在正确的位置。 所以最后所有来自未排序列表的元素都被排序。参考以下代码实现 -
def selection_sort(input_list):for idx in range(len(input_list)):min_idx = idxfor j in range( idx +1, len(input_list)):if input_list[min_idx] > input_list[j]:min_idx = j
# Swap the minimum value with the compared valueinput_list[idx], input_list[min_idx] = input_list[min_idx], input_list[idx]l = [19,2,31,45,30,11,121,27]
selection_sort(l)
print(l)
执行上面示例代码,得到以下结果 -
[2, 11, 19, 27, 30, 31, 45, 121]
相关文章:

python排序算法
排序是指以特定格式排列数据。 排序算法指定按特定顺序排列数据的方式。 最常见的排序是数字或字典顺序。 排序的重要性在于,如果数据是以分类方式存储,数据搜索可以优化到非常高的水平。 排序也用于以更易读的格式表示数据。 下面来看看python中实现的5…...

【C++入门第二期】引用 和 内联函数 的使用方法及注意事项
前言引用的概念初识引用区分引用和取地址引用与对象的关系引用的特性引用的使用场景传值和引用性能比较引用和指针的区别内联函数内联函数的概念内联函数的特性前言 本文主要学习的是引用 及 内联含函数,其中的引用在实际使用中会异常舒适。 引用的概念 概念&…...
数据结构——顺序表讲解
作者:几冬雪来 时间:2023年2月25日 内容:数据结构顺序表内容讲解 目录 前言: 顺序表: 1.线性表: 2.什么是顺序表: 3.顺序表的概念和构成: 4.顺序表的书写: 1…...
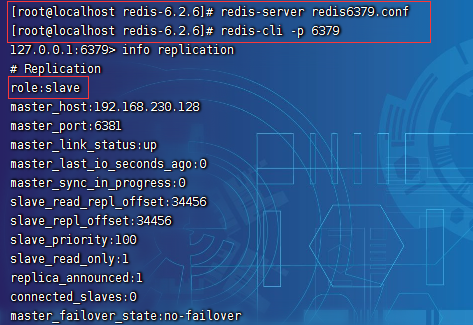
Redis 主从复制-服务器搭建【薪火相传/哨兵模式】
Redis 安装参考文章:Centos7 安装并启动 Redis-6.2.6 注意:本篇文章操作,不能在 静态IP地址 下操作,必须是 动态IP地址,否则最后主从服务器配置不成功! 管道符查看所有redis进程:ps -ef|grep re…...
分组查询)
数据库|(五)分组查询
(五)分组查询1. 介绍2. 语法3. 简单分组函数2. 添加筛选条件3. 添加复杂的筛选条件4. 分组查询特点5. 按表达式或函数分组6. 按多个字段分组7. 分组查询添加排序1. 介绍 引入:查询每个部门的平均工资 -- 以前写法:求的是总平均工…...

Orin安装ssh、vnc教程
文章目录一:ssh远程终端的配置PC的配置MobaXterm的下载二:VNC Viewer远程图形界面终端配置:PC配置:一:ssh远程 终端的配置 1.ifconfig查看终端ip地址 其中的eth是网口,我们需要看的是wlan0下的inet&#…...
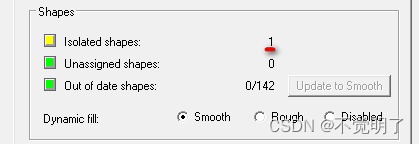
Allegro如何快速删除孤立铜皮操作指导
Allegro如何快速删除孤立铜皮操作指导 在做PCB设计的时候,铺铜是常用的设计方式,在PCB设计完成之后,需要删除PCB上孤立的铜皮,即铜皮有网络但是却没有任何连接 如下图 通过Status报表也可以看到Isolated shapes 如何快速地删除孤立铜皮,具体操作如下 点击Shape...

从单管单色到单管RGB,这项MicroLED工艺不可忽视
微显示技术商Porotech,在CES 2023期间展示了最新的MicroLED显示模组。近期,AR/VR光学领域的知名博主Karl Guttag深度分析了该公司的微显示技术,并指出Porotech带来了他见过最有趣的MicroLED技术。Guttag表示:Porotech是本届CES上给…...

6-Java中新建一个文件、目录、路径
文章目录前言1-文件、目录、路径2-在当前路径下创建一个文件3-在当前路径下创建一个文件夹(目录)3.1 测试1-路径已经存在3.2 测试2-路径不存在3.2 创建不存在的路径并新建文件3.3 删除已存在的文件并新建4-总结前言 学习Java中如何新建文件、目录、路径…...

Bootstrap系列之Flex布局
文章目录Bootstrap中的Flexd-flex与d-inline-flex也存在响应式变化flex水平布局flex垂直布局flex水平与垂直也存在响应式变化内容排列(justify-content响应式变化也存在于这里sm,md,lg,xl)子元素对齐方式Align items&a…...
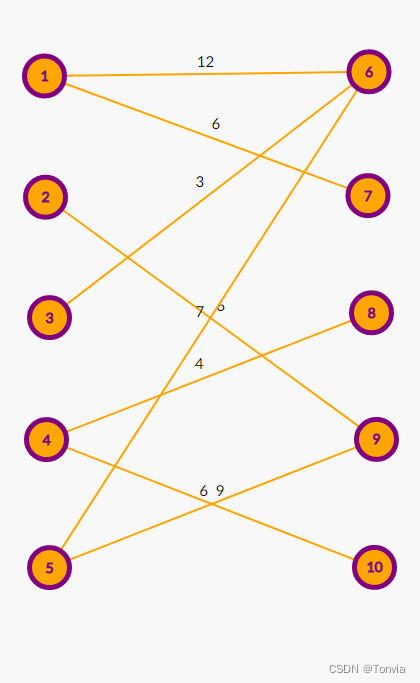
匈牙利算法与KM算法的区别
前记 在学习过程中,发现很多博客将匈牙利算法和KM算法混为一谈,当时只管用不管分析区别,所以现在来分析一下两个算法之间的区别。 匈牙利算法在二分图匹配的求解过程中共两个原则: 1.最大匹配数原则 2.先到先得原则 而KM算法求…...

You Only Need 90K Parameters to Adapt Light 论文阅读笔记
这是BMVC2022的论文,提出了一个轻量化的局部全局双支路的低光照图像质量增强网络,有监督。 思路是先用encoder f(⋅)f(\cdot)f(⋅)转到raw-RGB域,再用decoder gt(⋅)g_t(\cdot)gt(⋅)模拟ISP过程转到sRGB域。虽然文章好像没有明确指出&…...
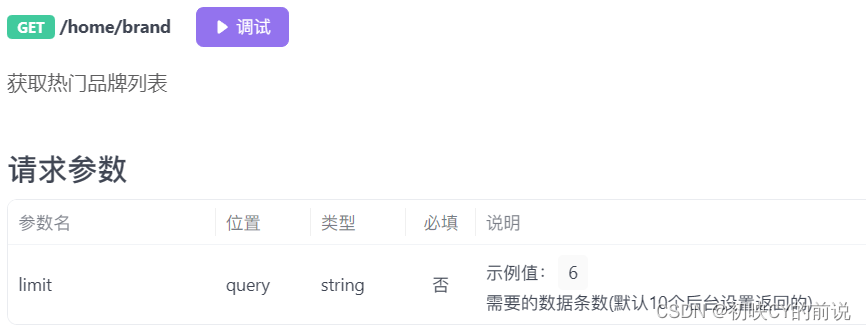
【vue2小知识】实现axios的二次封装
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:在vue2中实现axios的二次封装 目录 一、平常axios的请求发送方式 二、axios的一次封装…...

走近php的数组:数组的定义与数组函数
数组是一种数据结构,它由一组元素组成,这些元素可以是相同类型或不同类型。数组是在程序运行时动态创建的,可以根据需要增加或删除元素,因此它们是非常灵活和实用的数据结构。在大多数编程语言中,数组都有一个索引&…...
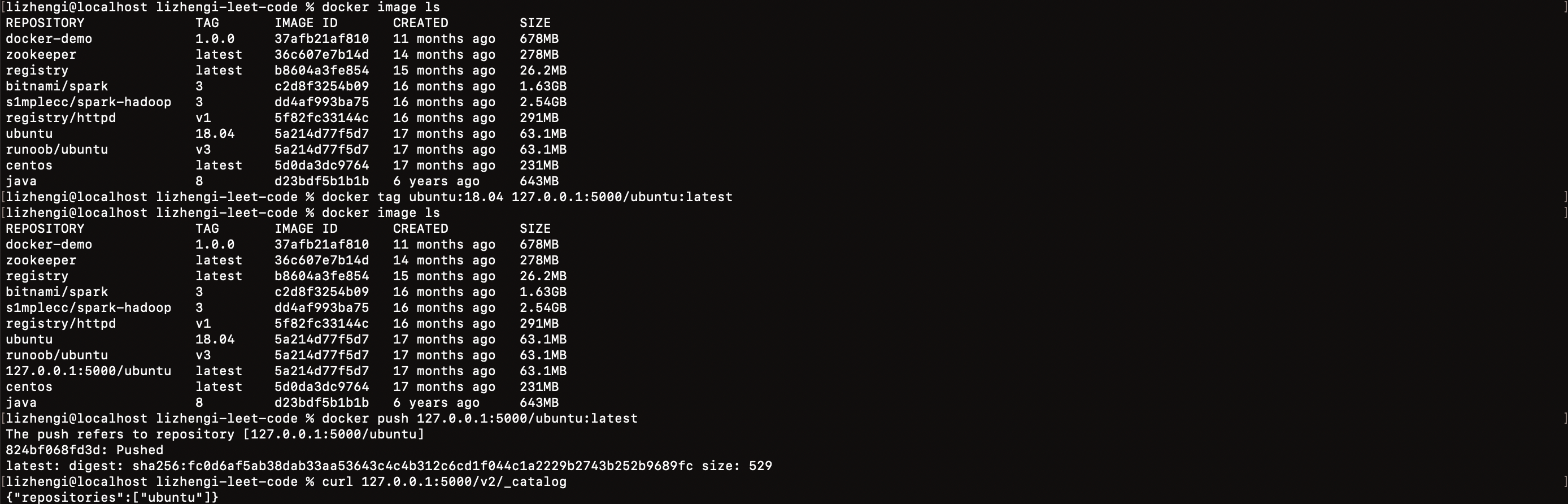
Docker 应用实践-仓库篇
目前 Docker 官方维护了一个公共仓库 Docker Hub,用于查找和与团队共享容器镜像,界上最大的容器镜像存储库,拥有一系列内容源,包括容器社区开发人员、开放源代码项目和独立软件供应商(ISV)在容器中构建和分…...
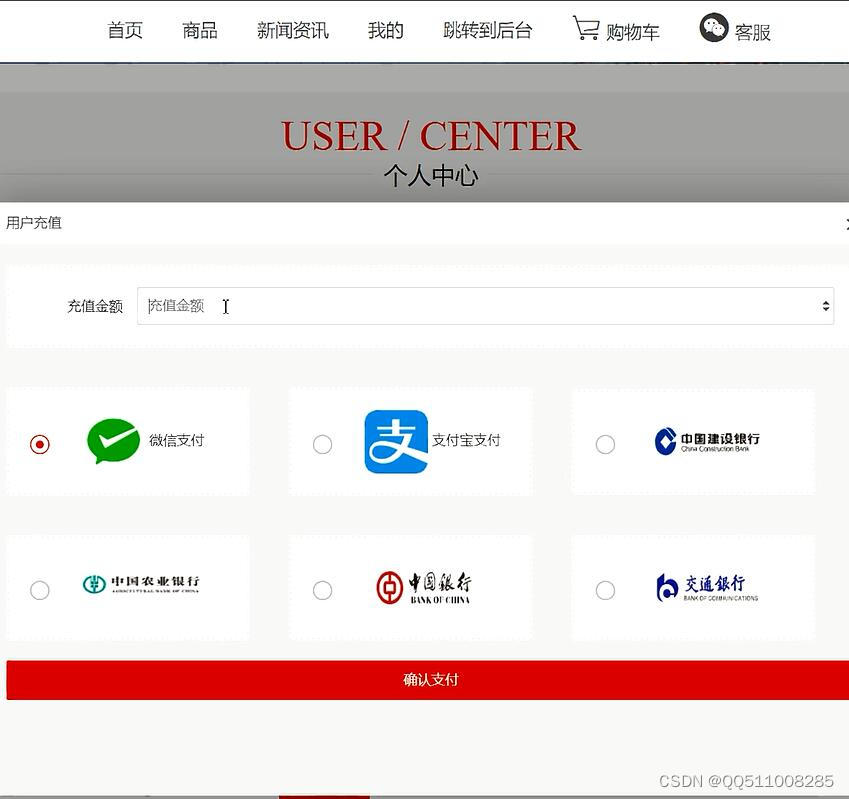
python+django篮球NBA周边商城vue
目 录 第一章 绪 论 1 1.1背景及意义 1 1.2国内外研究概况 1 1.3 研究的内容 1 第二章 关键技术的研究 3 2.1 vue技术介绍 3 myproject/ <-- 高级别的文件夹 |-- myproject/ <-- Django项目文件夹 | |-- myproje…...
抽象类与接口的区别
抽象类什么是抽象类?抽象类是特殊的类,只是不能被实例化;除此以外,具有类的其他特性;重要的是抽象类可以包括抽象方法,这是普通类所不能的。抽象方法只能声明于抽象类中,且不包含任何实现&#…...

1904. 你完成的完整对局数
题目: 一款新的在线电子游戏在近期发布,在该电子游戏中,以 刻钟 为周期规划若干时长为 15 分钟 的游戏对局。这意味着,在 HH:00、HH:15、HH:30 和 HH:45 ,将会开始一个新的对局,其中 HH 用一个从 00 到 23…...

Vue3:自定义指令以及简单的后台管理权限封装
目录 前言: 自定义指令介绍: 局部的自定义指令: 全局自定义指令: 讲讲后台管理权限管理: 前言: 说起这个自定义指令的使用场景,我第一反应就是,后台管理的权限管理,要…...
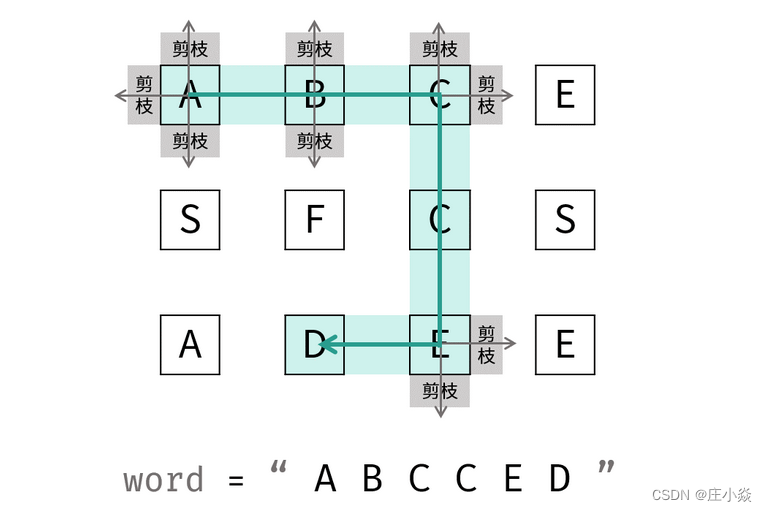
剑指 Offer 12. 矩阵中的路径
摘要 剑指 Offer 12. 矩阵中的路径 一、回溯算法解析 本问题是典型的矩阵搜索问题,可使用 深度优先搜索(DFS) 剪枝解决。 深度优先搜索: 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归,先朝一个方向搜…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
