P5461 赦免战俘
题目描述
现有 2 n × 2 n ( n ≤ 10 ) 2^n\times 2^n (n\le10) 2n×2n(n≤10) 名作弊者站成一个正方形方阵等候 kkksc03 的发落。kkksc03 决定赦免一些作弊者。他将正方形矩阵均分为 4 个更小的正方形矩阵,每个更小的矩阵的边长是原矩阵的一半。其中左上角那一个矩阵的所有作弊者都将得到赦免,剩下 3 个小矩阵中,每一个矩阵继续分为 4 个更小的矩阵,然后通过同样的方式赦免作弊者……直到矩阵无法再分下去为止。所有没有被赦免的作弊者都将被处以棕名处罚。
给出 n n n,请输出每名作弊者的命运,其中 0 代表被赦免,1 代表不被赦免。
输入格式
一个整数 n n n。
输出格式
2 n × 2 n 2^n \times 2^n 2n×2n 的 01 矩阵,代表每个人是否被赦免。数字之间有一个空格。
样例输入
3
样例输出
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 1
0 0 0 0 0 1 0 1
0 0 0 0 1 1 1 1
0 0 0 1 0 0 0 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
1 1 1 1 1 1 1 1
问题分析
2n 就是n个2相乘。比如,21 =2,22 =4,25 =32,210 =1024。
2n 可以被一直除以2进行均分,直到只剩1为止。
长度是2n的一维数组,可以被一直均分成两份,直到只剩一个格子为止。
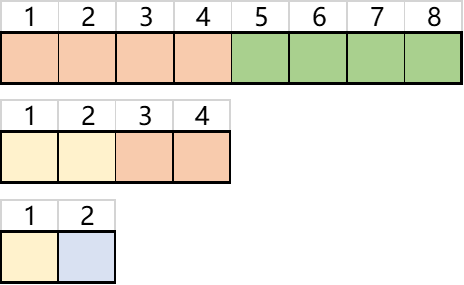
2n × 2n 的二维数组(矩阵),可以被一直均分成4份,直到只剩一个格子为止。
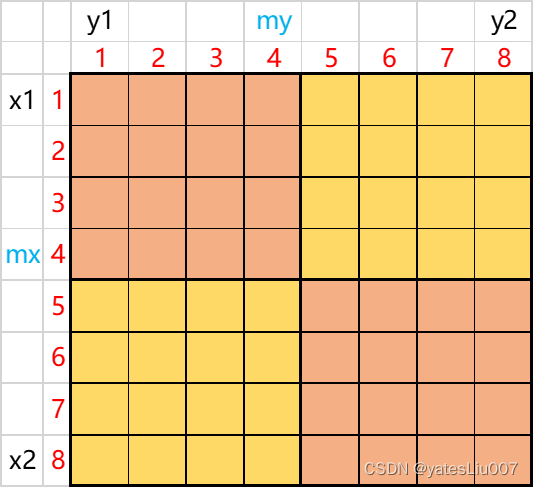

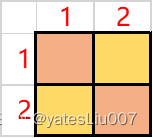
如何使用代码将矩阵均分成4份呢?
用(x1,y1)表示左上角的格子,(x2,y2)表示右下角的格子,那么(x1,y1)和(x2,y2)就确定了一个唯一 的矩阵。
如果找到了被均分成的4个小矩阵的左上格子和右下格子,那么4个小矩阵也就被确定了。
令 mx = (x1+x2)/2 , my=(y1+y2)/2,就可以得到如下结果:
- 左上方的1/4矩阵,左上角的格子是(x1,y1),右下角的格子是( mx, my)。
- 右上方的1/4矩阵,左上角的格子是(x1,my+1),右下角的格子是( mx, y2)。
- 左下方的1/4矩阵,左上角的格子是(mx+1,
y1),右下角的格子是( x2, my)。 - 右下方的1/4矩阵,左上角的格子是(mx+1, my+1),右下角的格子是( x2, y2)。
C++中,通过位运算 1<<n 可以快速计算出 2n的值。
由于 n≤10 ,所以,数组的行列数可以设置为 (1<<10)+5。
作弊者只有被赦免和不被赦免两种状态,定义成bool类型数组就够了。
将矩阵不断均分的过程可以用递归函数实现。递归结束条件是,矩阵只有1×1大小,这个时候就不能继续均分了。
递归步骤如下:
1、计算出mx,my;
2、将左上矩阵中的值改为true。
3、递归处理右上、左下和右下的矩阵
参考代码
#include<bits/stdc++.h>
using namespace std;
const int M=(1<<10)+5;
bool a[M][M]; //a[i][j]=true表示被赦免,否则表示不被赦免
//(x1,y1)-正方形左上角;(x2,y2)-正方形右下角
void dfs(int x1,int y1,int x2,int y2) {//当(x1,y1)和(x2,y2)指向同一个格子时,不能再分。if(x1==x2&&y1==y2) return;//否则,继续将正方形均分成4个更小的正方形//计算左上正方形的左下角方格下标int mx=(x1+x2)/2,my=(y1+y2)/2; //左上角的赦免for(int i=x1; i<=mx; i++)for(int j=y1; j<=my; j++)a[i][j]=true;//递归处理其他3个小矩阵dfs(x1,my+1,mx,y2); //右上dfs(mx+1,y1,x2,my); //左下 dfs(mx+1,my+1,x2,y2); //右下
}
int main() {int n;cin>>n;n=1<<n;dfs(1,1,n,n);//按要求输出:0 代表被赦免,1 代表不被赦免。for(int i=1; i<=n; i++) {for(int j=1; j<=n; j++)printf("%d ",!a[i][j]);printf("\n");}return 0;
}
相关文章:

P5461 赦免战俘
题目描述 现有 2 n 2 n ( n ≤ 10 ) 2^n\times 2^n (n\le10) 2n2n(n≤10) 名作弊者站成一个正方形方阵等候 kkksc03 的发落。kkksc03 决定赦免一些作弊者。他将正方形矩阵均分为 4 个更小的正方形矩阵,每个更小的矩阵的边长是原矩阵的一半。其中左上角那一个矩阵…...

【工具】转码silk格式为mp3
【工具】转码slk格式为mp3 前提 安装 ffmpeg 【安装】Linux安装ffmpeg_linux安装ffmpeg4.4_我是Superman丶的博客-CSDN博客 GitHub - kn007/silk-v3-decoder: [Skype Silk Codec SDK]Decode silk v3 audio files (like wechat amr, aud files, qq slk files) and convert to o…...

蓝桥杯每日一题2023.10.18
题目描述 特别数的和 - 蓝桥云课 (lanqiao.cn) 题目分析 简单枚举每一个可行的数 #include<bits/stdc.h> using namespace std; int flag, ans; int main() {int n;cin >> n;for(int i 1; i < n; i ){flag 0;int x i;while(x){int y x % 10;if(y 2 || y…...
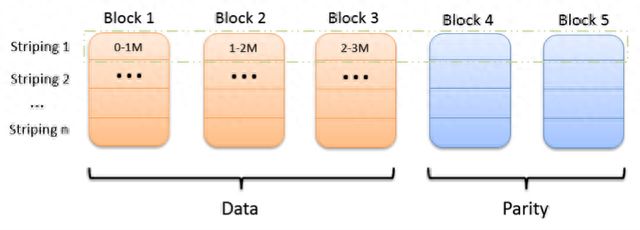
大数据开发中的秘密武器:探索Hadoop纠删码的奇妙世界
随着大数据技术的发展,HDFS作为Hadoop的核心模块之一得到了广泛的应用。为了系统的可靠性,HDFS通过复制来实现这种机制。但在HDFS中每一份数据都有两个副本,这也使得存储利用率仅为1/3,每TB数据都需要占用3TB的存储空间。因此&…...

华为数通方向HCIP-DataCom H12-831题库(单选题:301-310)
第301题 关于配置防火墙安全区域的安全级别的描述,错误的是 A、同一系统中,两个安全区域不允许配置相同的安全级别 B、只能为自定义的安全区域设定安全级别 C、安全级别一旦设定不允许更改 D、新建的安全区域,系统默认其安全级别为1 答案:D 解析: 新创建的安全区域缺省未…...
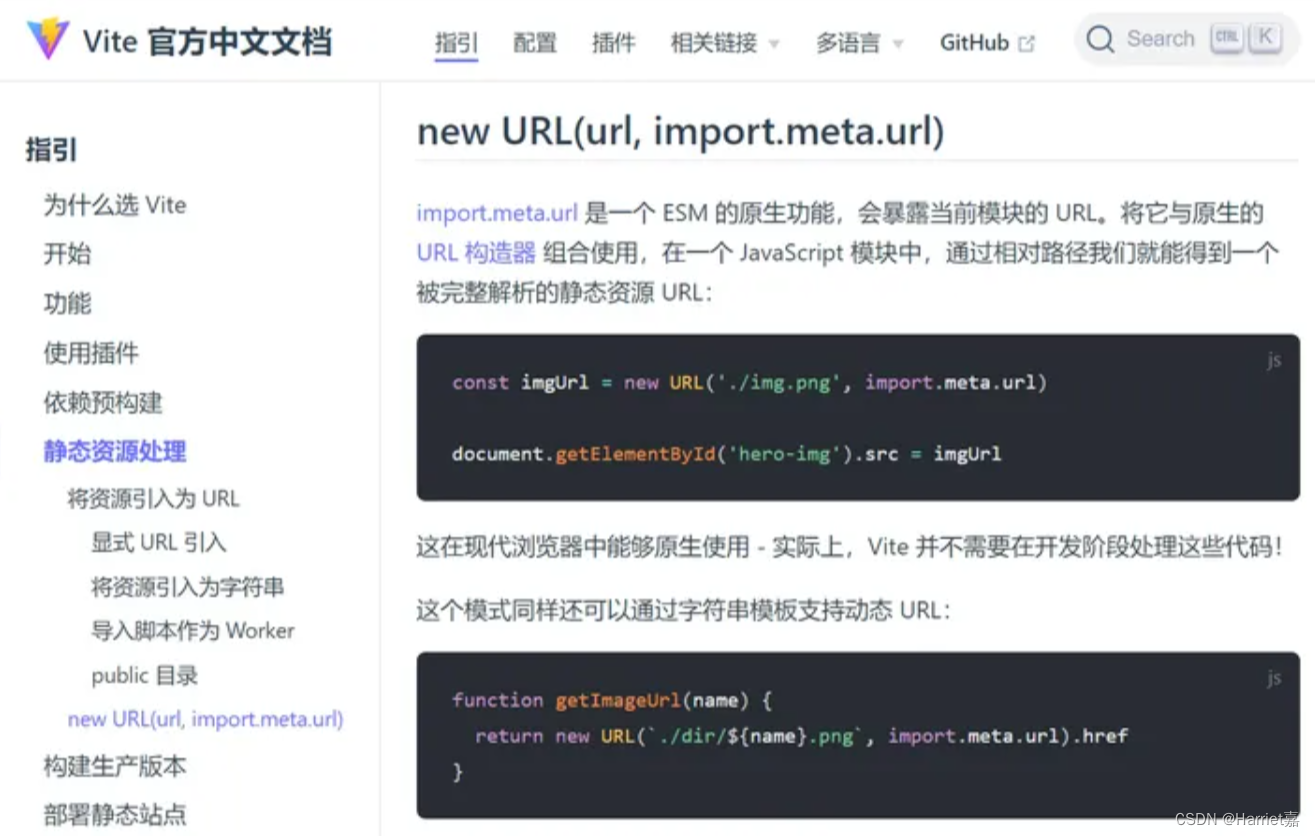
Vite 踩坑 —— require is not defined
动态require引入图片报错 require 是属于 Webpack 的方法,而我使用的是 Vite,所以我们需要去寻找 Vite 静态资源处理的方法 所以,我们只需要将代码改写以下形式即可。 template <CarouselItem v-for"(item,index) of carous…...

彻底理解操作系统与内核的区别!
通用底盘技术 Canoo公司有一项核心技术专利,这就是它们的通用电动底盘技术,长得是这个样子,非常像一个滑板: 这个带轮子、有电池、能动的滑板已经包含了一辆车最核心的组件,差的就是一个外壳。这个看起来像滑板的东西…...

微信小程序4
一自定义组件应用 1.介绍 微信小程序自定义组件是指开发者可以自定义组件,将一些常用的 UI 元素封装成一个自定义组件,然后在多个页面中复用该组件,实现代码复用和页面性能优化的效果。 2.自定义组件分为两种类型 组件模板类型:…...

OpenCV14-图像平滑:线性滤波和非线性滤波
OpenCV14-图像平滑:线性滤波和非线性滤波 1.图像滤波2.线性滤波2.1均值滤波2.2方框滤波2.3高斯滤波2.4可分离滤波 3.非线性滤波3.1中值滤波3.2双边滤波 1.图像滤波 图像滤波是指去除图像中不重要的内容,而使关心的内容表现得更加清晰的方法,…...

kafka_2.10启动Kafka broker
要启动 Kafka broker,你需要执行以下步骤: 首先,确保你已经安装了 Kafka。你可以从 Apache Kafka 的官方网站下载 Kafka 的二进制发行版,并按照官方文档中的说明进行安装。 在安装完成后,进入 Kafka 的安装目录。 打…...
【配置环境】SQLite数据库安装和编译以及VS下C++访问SQLite数据库
一,环境 Windows 11 家庭中文版,64 位操作系统, 基于 x64 的处理器SQLite - 3.43.2Microsoft Visual Studio Community 2022 (64 位) - Current 版本 17.5.3 二,SQLite简介 简要介绍 SQLite(Structured Query Language for Lite&a…...
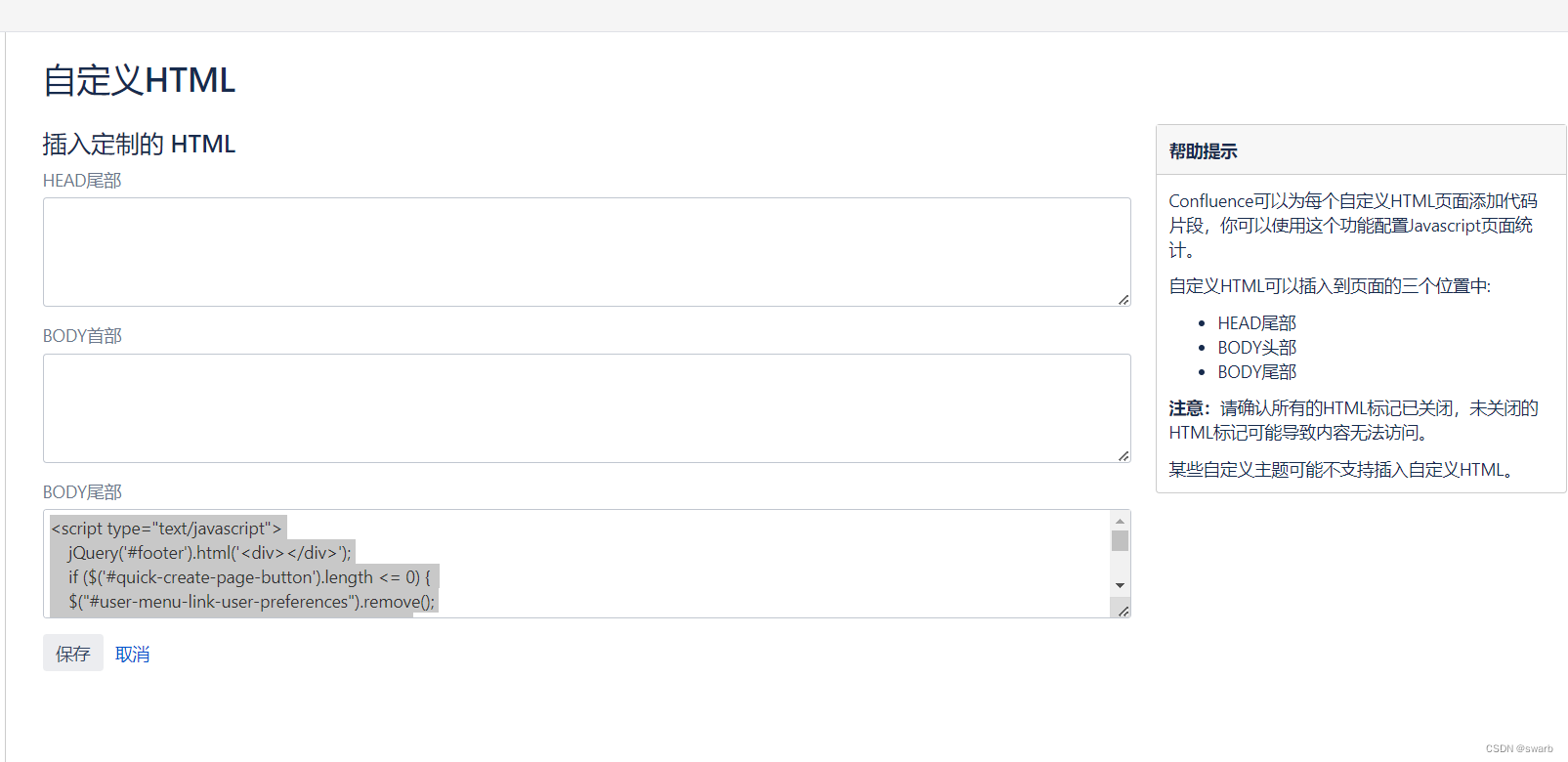
Confluence 自定义展示页面
1. 概述 Confluence 作为知识库可通过JS脚本方式,根据登录用户或用户组进行前端页面的自定义 2. 实现方式 Confluence →管理→自定义HTML 嵌入对应JS脚本,示例如下 <script type"text/javascript">jQuery(#footer).html(<div>…...

使用C#的Socket从头实现的带有文件上传和下载功能的HTTP服务器
使用C#和Socket从头实现的带有文件上传和下载功能的HTTP服务器。它支持GET、POST请求方法,并能处理URL参数、请求体以及文件上传和下载。 using System; using System.IO; using System.Net; using System.Net.Sockets; using System.Text;class HttpServer {publi…...

【OSPF Loading、FULL状态与display ospf peer brief命令、OSPF的数据库讲解】
个人名片: 🐼作者简介:一名大二在校生,喜欢编程🎋 🐻❄️个人主页🥇:落. 🐼个人WeChat:hmmwx53 🕊️系列专栏:🖼️ 零基…...

除氟树脂在工业、市政含氟废水处理中的应用
含氟废水的不达标排放对自然环境有很大的危害,氟化物离子可以累积在土壤和水体中,从而对生态系统造成破坏。大量的氟化物离子会对植物生长产生不良影响,并对水生生物造成毒性作用,严重时还可能导致生态灾难。氟化物离子如果没有得…...

模拟地和数字地的区别
模拟地和数字地的主要区别体现在设计目的、处理技术、数据类型和数据精度四个方面。 设计目的:模拟地的主要设计目的是分析时空数据、进行模型和预测,它主要关注动态变化和过程。而数字地的主要设计目的是数据的存储、管理、查询和分析,在地…...

Druid连接池最小连接数设置失效问题
问题发现: 配置 当项目启动后 线程池确实是初始化了5条连接,但是当项目运行一段时间后,5条连接确消失了,只会程序用到得时候,再去初始化连接,这样有点违背了参数设置得意义,后来通过查阅资料发…...

Javascript数据类型和类型转换
Javascript数据类型和类型转换 在JavaScript中,理解数据类型,如何区分它们,以及它们如何被转换是至关重要的。在这篇文章中,我们将探讨这些主题,以帮助巩固你的JavaScript基础。 基础数据类型和引用数据类型 当涉及…...
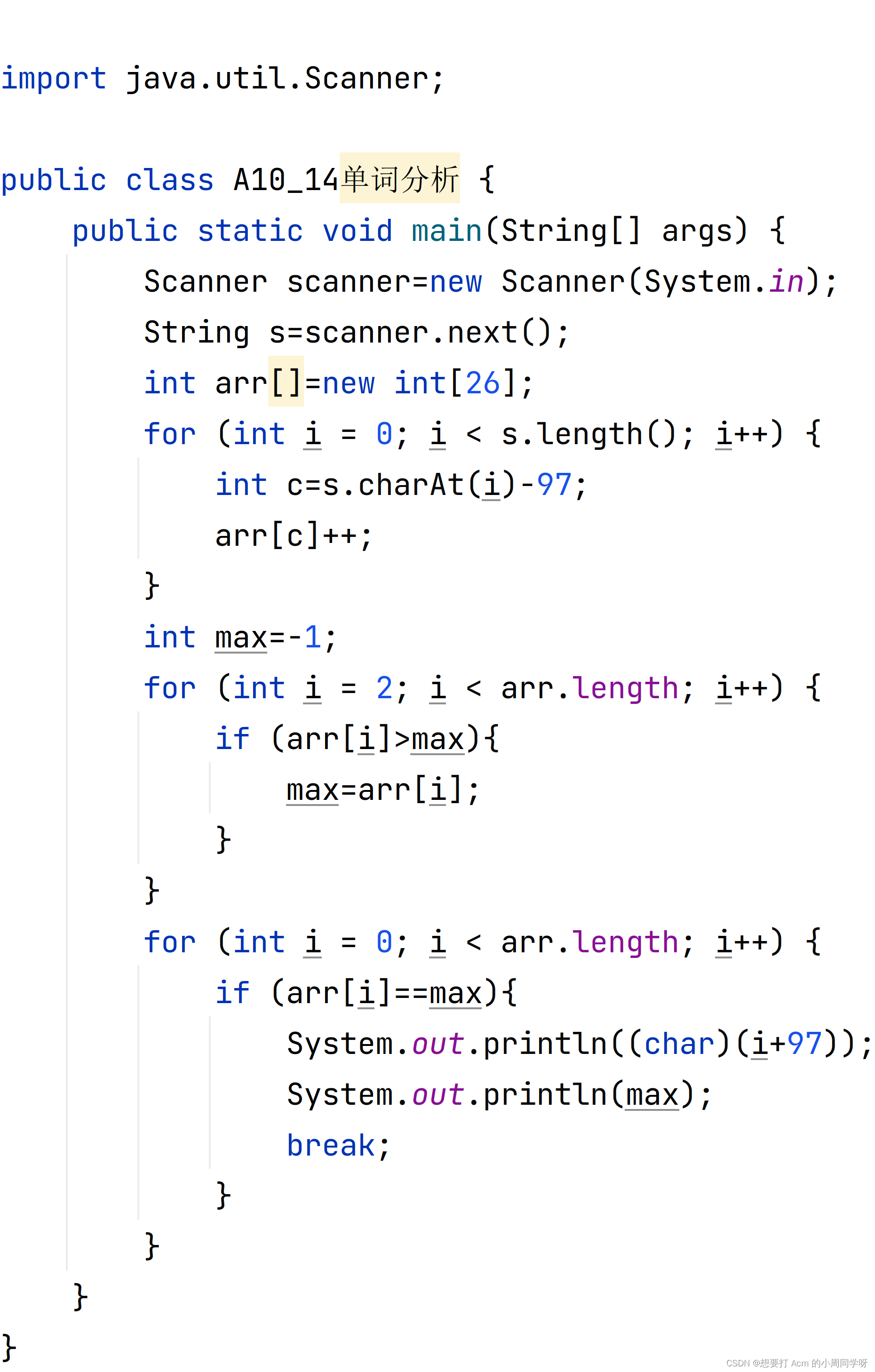
冲刺十五届蓝桥杯P0005单词分析
文章目录 题目分析代码 题目 单词分析 分析 统计字符串中字母出现的次数,可以采用哈希表,代码采用的是数组来存储字符,将字符-97,得到对应的数组下标,将对应下标的数组;找到数组元素最大的下标ÿ…...
php获取10年内的年份并加入下拉列表
要实现的效果 在html中内嵌php循环将数组中的年份加入下拉列表 <div class="form-group"><label>年份:</label><div class="input-group"><div class="input-group-prepend"><span class="input-group-te…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
