494.目标和 474.一和零
目标和
题目
给一个都是正整数的组合,然后你可以在里面任意添加+或-,求使得最后结果为
目标和S(target)的有多少种方法?
范围
- 数组非空,且长度不会超过 20 。
- 初始的数组的和不会超过 1000 。
- 保证返回的最终结果能被 32 位整数存下。
思路
用背包方法的话,这是怎么带入背包方法的?任意添加+或-后会分成两个组合
+是left(总和),-是right(总和),如果结果为目标和target的话,sum=left+right(总和),target=left-right(目标和),推出right=left-target 推出sum=left+(left-target)最后推出 left=(target+sum)/2,利用target和sum都确定这一点,可以求出+的组合left来。
带入背包问题
假设加法的总和为x(left),那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = target
x = (target + sum) / 2
此时问题就转化为,装满容量为x的背包,有几种方法。
这个时候装满了容量为x的背包相当于,任意+或者-之后的目标值被满足了。
这里如果x = (target + sum) / 2没有被整除,说明最后目标值不能为target,说明没有方案
同时如果 S的绝对值大于sum,那么也没有方案
递推公式
dp[j] += dp[j - nums[i]]dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法,nums[i]是那个都是正整数的组合的第i个数,方法不同的方法就不考虑放还是不放了,都放进去,然后累加起来。比如
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
- 他们的dp[1-5]种方法都加起来。
初始化
dp[0]=1,为什么?不知道,按定义来,容量为0的背包的最大方法数为1,+0和-0是一种方法吗?总之dp[0]=1能通过
总代码
class Solution {
public:int findTargetSumWays(vector<int>& nums, int S) {int sum = 0;for (int i = 0; i < nums.size(); i++) sum += nums[i];if (abs(S) > sum) return 0; // 此时没有方案if ((S + sum) % 2 == 1) return 0; // 此时没有方案int bagSize = (S + sum) / 2;vector<int> dp(bagSize + 1, 0);dp[0] = 1;for (int i = 0; i < nums.size(); i++) {for (int j = bagSize; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagSize];}
};这题也挺抽象的
一和零
题目
给一个元素只由0和1组成的集合strs,再给两个正整数m和n,要求找出最多有m个0和n个1的集合strs的子集,同时这个子集的元素最多。
示例 :
- 输入:strs = ["10", "0", "1"], m = 1, n = 1
- 输出:2
- 解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
思路
带入背包问题,相当于把strs的每个元素作为物品,每个物品计算他们的0和1的数量,然后执行放和不放最多承载m个0和n个1背包的操作,区别不过这里有0,1两个维度而已。
m 和 n 和 元素最多的子集 是3个维度,用二维数组dp[i][j],意思是最多m个0和n个1的集合的最大元素个数是dp[i][j],然后套用01背包公式求出结果就行了。
递推公式
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);由01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i])得来,
zeroNum oneNum相当于之前的重量weight[i],dp[i][j]和dp[i - zeroNum][j - oneNum]的意思还是放入还是不放入的意思,不过由之前只有 j 的一个维度变成了 i 和 j 的两个维度,加1是相当于之前的价值value[i],因为每次遍历的是单个字符串,所以只能+1.
初始化
物品价值不会为负数,初始化为0
vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0));遍历顺序
一维度的01背包都是后续遍历,这里虽然像两维度的,但却是两个相同维度的一维度,所以顺序先遍历那边都行,我是这样理解的。
总代码
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0for (string str : strs) { // 遍历每个物品,也就是每个字符串int oneNum = 0, zeroNum = 0;for (char c : str) {//遍历当前物品也就是当前的字符串的0和1数量if (c == '0') zeroNum++;else oneNum++;}//用上面得到当前字符串的0和1数量for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历!for (int j = n; j >= oneNum; j--) {dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}//注意第一个for到这里才结束return dp[m][n];}
};这题也蛮抽象的
相关文章:

494.目标和 474.一和零
目标和 题目 给一个都是正整数的组合,然后你可以在里面任意添加或-,求使得最后结果为 目标和S(target)的有多少种方法? 范围 数组非空,且长度不会超过 20 。初始的数组的和不会超过 1000 。保证返回的…...

模拟电源与数字电源之间的区别
BOSHIDA 模拟电源与数字电源之间的区别 模拟电源与数字电源是两种不同的电源类型,其核心区别在于电源控制方式和输出特性。本文将从这两方面对模拟电源和数字电源进行比较和分析。 电源控制方式: 模拟电源的控制方式以模拟电压和模拟电流为基础。模拟电…...
P5461 赦免战俘
题目描述 现有 2 n 2 n ( n ≤ 10 ) 2^n\times 2^n (n\le10) 2n2n(n≤10) 名作弊者站成一个正方形方阵等候 kkksc03 的发落。kkksc03 决定赦免一些作弊者。他将正方形矩阵均分为 4 个更小的正方形矩阵,每个更小的矩阵的边长是原矩阵的一半。其中左上角那一个矩阵…...

【工具】转码silk格式为mp3
【工具】转码slk格式为mp3 前提 安装 ffmpeg 【安装】Linux安装ffmpeg_linux安装ffmpeg4.4_我是Superman丶的博客-CSDN博客 GitHub - kn007/silk-v3-decoder: [Skype Silk Codec SDK]Decode silk v3 audio files (like wechat amr, aud files, qq slk files) and convert to o…...

蓝桥杯每日一题2023.10.18
题目描述 特别数的和 - 蓝桥云课 (lanqiao.cn) 题目分析 简单枚举每一个可行的数 #include<bits/stdc.h> using namespace std; int flag, ans; int main() {int n;cin >> n;for(int i 1; i < n; i ){flag 0;int x i;while(x){int y x % 10;if(y 2 || y…...
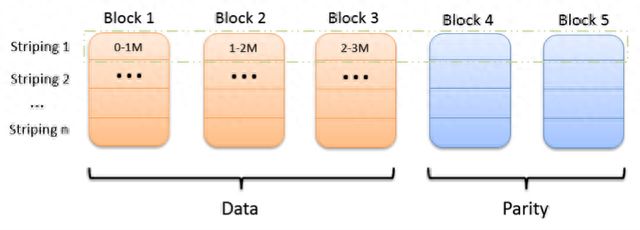
大数据开发中的秘密武器:探索Hadoop纠删码的奇妙世界
随着大数据技术的发展,HDFS作为Hadoop的核心模块之一得到了广泛的应用。为了系统的可靠性,HDFS通过复制来实现这种机制。但在HDFS中每一份数据都有两个副本,这也使得存储利用率仅为1/3,每TB数据都需要占用3TB的存储空间。因此&…...

华为数通方向HCIP-DataCom H12-831题库(单选题:301-310)
第301题 关于配置防火墙安全区域的安全级别的描述,错误的是 A、同一系统中,两个安全区域不允许配置相同的安全级别 B、只能为自定义的安全区域设定安全级别 C、安全级别一旦设定不允许更改 D、新建的安全区域,系统默认其安全级别为1 答案:D 解析: 新创建的安全区域缺省未…...
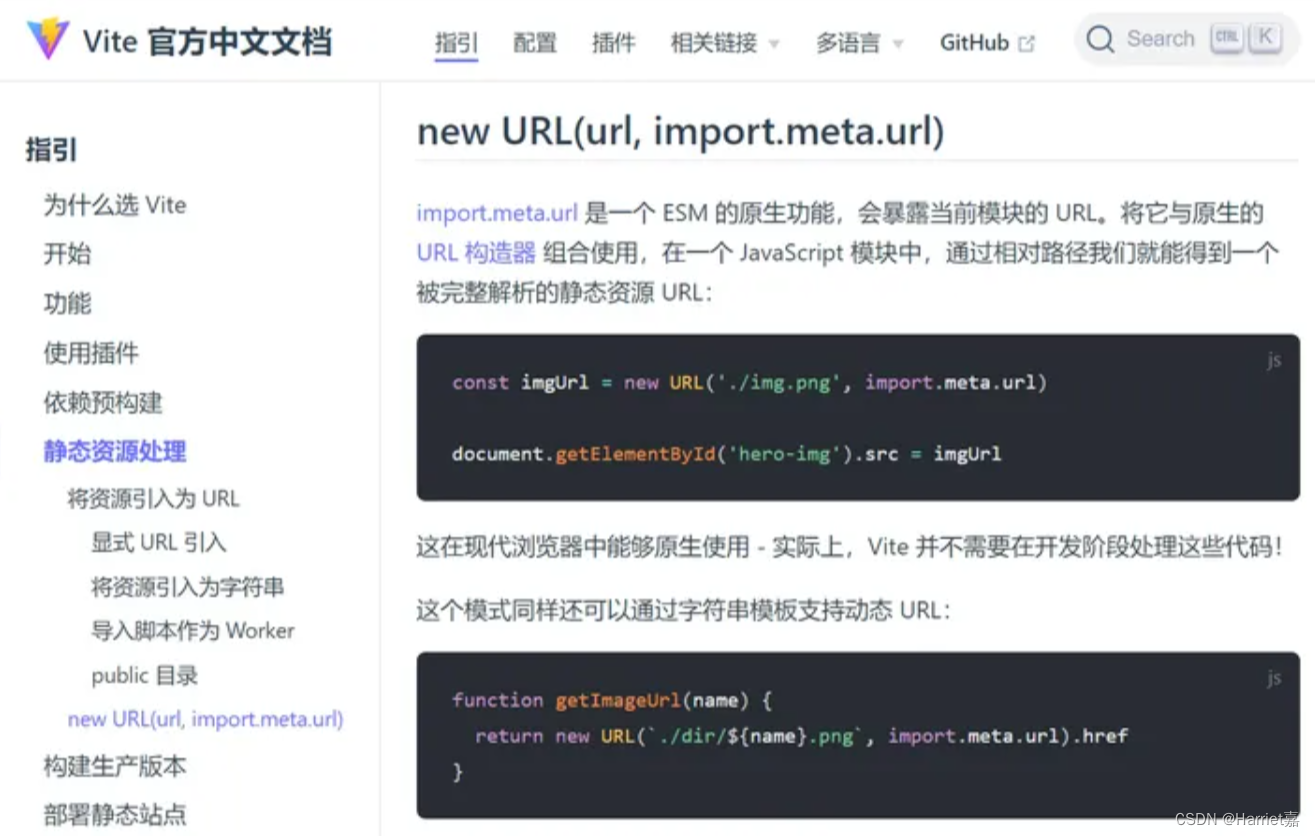
Vite 踩坑 —— require is not defined
动态require引入图片报错 require 是属于 Webpack 的方法,而我使用的是 Vite,所以我们需要去寻找 Vite 静态资源处理的方法 所以,我们只需要将代码改写以下形式即可。 template <CarouselItem v-for"(item,index) of carous…...

彻底理解操作系统与内核的区别!
通用底盘技术 Canoo公司有一项核心技术专利,这就是它们的通用电动底盘技术,长得是这个样子,非常像一个滑板: 这个带轮子、有电池、能动的滑板已经包含了一辆车最核心的组件,差的就是一个外壳。这个看起来像滑板的东西…...

微信小程序4
一自定义组件应用 1.介绍 微信小程序自定义组件是指开发者可以自定义组件,将一些常用的 UI 元素封装成一个自定义组件,然后在多个页面中复用该组件,实现代码复用和页面性能优化的效果。 2.自定义组件分为两种类型 组件模板类型:…...

OpenCV14-图像平滑:线性滤波和非线性滤波
OpenCV14-图像平滑:线性滤波和非线性滤波 1.图像滤波2.线性滤波2.1均值滤波2.2方框滤波2.3高斯滤波2.4可分离滤波 3.非线性滤波3.1中值滤波3.2双边滤波 1.图像滤波 图像滤波是指去除图像中不重要的内容,而使关心的内容表现得更加清晰的方法,…...

kafka_2.10启动Kafka broker
要启动 Kafka broker,你需要执行以下步骤: 首先,确保你已经安装了 Kafka。你可以从 Apache Kafka 的官方网站下载 Kafka 的二进制发行版,并按照官方文档中的说明进行安装。 在安装完成后,进入 Kafka 的安装目录。 打…...
【配置环境】SQLite数据库安装和编译以及VS下C++访问SQLite数据库
一,环境 Windows 11 家庭中文版,64 位操作系统, 基于 x64 的处理器SQLite - 3.43.2Microsoft Visual Studio Community 2022 (64 位) - Current 版本 17.5.3 二,SQLite简介 简要介绍 SQLite(Structured Query Language for Lite&a…...
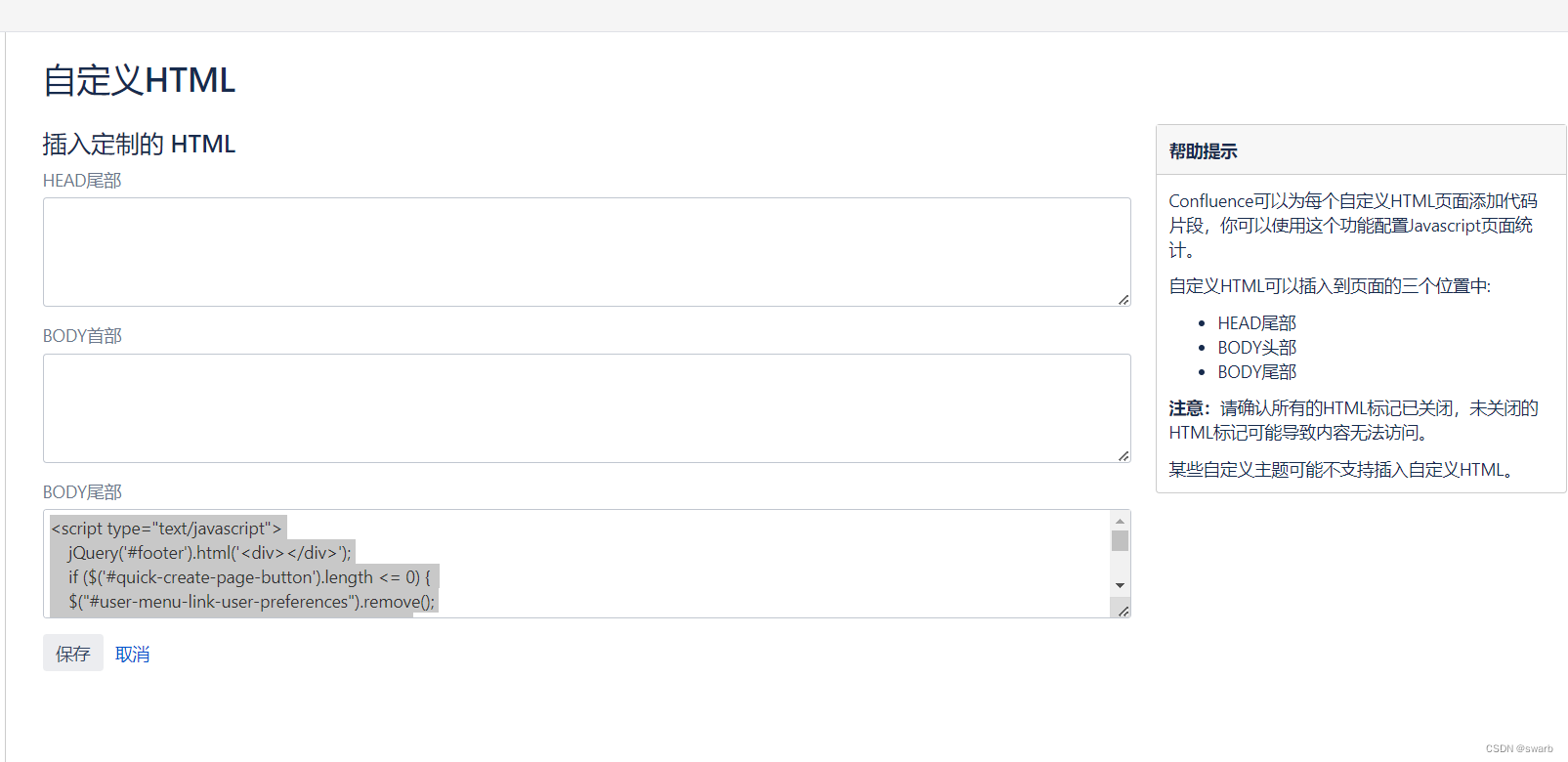
Confluence 自定义展示页面
1. 概述 Confluence 作为知识库可通过JS脚本方式,根据登录用户或用户组进行前端页面的自定义 2. 实现方式 Confluence →管理→自定义HTML 嵌入对应JS脚本,示例如下 <script type"text/javascript">jQuery(#footer).html(<div>…...

使用C#的Socket从头实现的带有文件上传和下载功能的HTTP服务器
使用C#和Socket从头实现的带有文件上传和下载功能的HTTP服务器。它支持GET、POST请求方法,并能处理URL参数、请求体以及文件上传和下载。 using System; using System.IO; using System.Net; using System.Net.Sockets; using System.Text;class HttpServer {publi…...

【OSPF Loading、FULL状态与display ospf peer brief命令、OSPF的数据库讲解】
个人名片: 🐼作者简介:一名大二在校生,喜欢编程🎋 🐻❄️个人主页🥇:落. 🐼个人WeChat:hmmwx53 🕊️系列专栏:🖼️ 零基…...

除氟树脂在工业、市政含氟废水处理中的应用
含氟废水的不达标排放对自然环境有很大的危害,氟化物离子可以累积在土壤和水体中,从而对生态系统造成破坏。大量的氟化物离子会对植物生长产生不良影响,并对水生生物造成毒性作用,严重时还可能导致生态灾难。氟化物离子如果没有得…...

模拟地和数字地的区别
模拟地和数字地的主要区别体现在设计目的、处理技术、数据类型和数据精度四个方面。 设计目的:模拟地的主要设计目的是分析时空数据、进行模型和预测,它主要关注动态变化和过程。而数字地的主要设计目的是数据的存储、管理、查询和分析,在地…...

Druid连接池最小连接数设置失效问题
问题发现: 配置 当项目启动后 线程池确实是初始化了5条连接,但是当项目运行一段时间后,5条连接确消失了,只会程序用到得时候,再去初始化连接,这样有点违背了参数设置得意义,后来通过查阅资料发…...

Javascript数据类型和类型转换
Javascript数据类型和类型转换 在JavaScript中,理解数据类型,如何区分它们,以及它们如何被转换是至关重要的。在这篇文章中,我们将探讨这些主题,以帮助巩固你的JavaScript基础。 基础数据类型和引用数据类型 当涉及…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...
