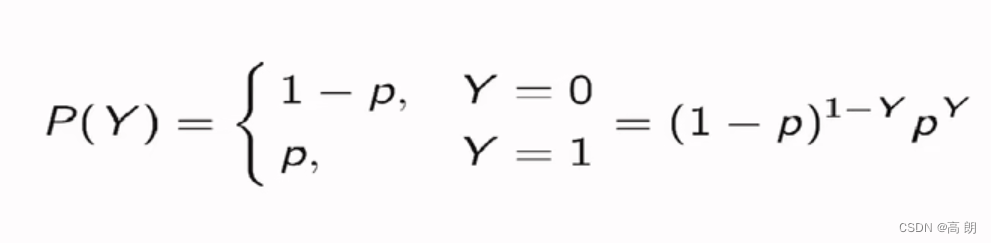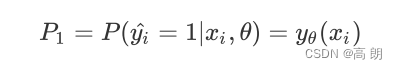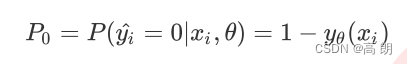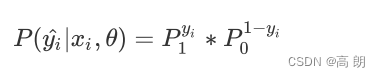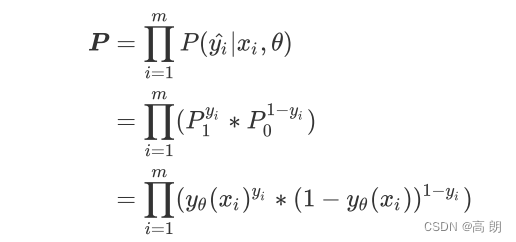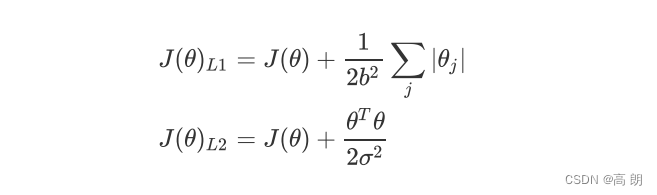【机器学习】逻辑回归
文章目录
- 逻辑回归
- 定义损失函数
- 正则化
- sklearn里面的逻辑回归
- 多项式逻辑回归
逻辑回归
逻辑回归,是一种名为“回归”的线性分类器,其本质是由线性回归变化而来的,一种广泛使用于分类问题中的广义回归算法。
线性回归是机器学习中最简单的的回归算法,它写作一个几乎人人熟悉的方程:
z = b + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n = θ T X , ( θ 0 = b ) z = b+θ_1x_1+θ_2x_2+...+θ_nx_n=θ^TX,(θ_0=b) z=b+θ1x1+θ2x2+...+θnxn=θTX,(θ0=b)
θ被统称为模型的参数,其中 b b b被称为截距(intercept), θ 1 θ_1 θ1 ~ θ n θ_n θn 被称为系数(coefficient)。此时我们的z是连续的,所以是回归模型。
线性回归的任务,就是构造一个预测函数z来映射输入的特征矩阵x和标签值y的线性关系,而构造预测函数的核心就是找出模型的参数:θ系数和 b,著名的最小二乘法就是用来求解线性回归中参数的数学方法。
如果想要z是离散的,也就是标签是离散型变量,则需要再做一次函数转换 g ( z ) g(z) g(z),并且令 g ( z ) g(z) g(z)的值分布在(0,1)之间,且当 g ( z ) g(z) g(z)接近0时样本的标签为类别0,当 g ( z ) g(z) g(z)接近1时样本的标签为类别1,这样就得到了一个分类模型。而这个联系函数对于逻辑回归来说,就是Sigmoid函数:
g ( z ) = 1 1 + e − z = 1 1 + e − θ T X g(z) = \frac{1}{1+e^{-z}}=\frac{1}{1+e^{-θ^TX}} g(z)=1+e−z1=1+e−θTX1
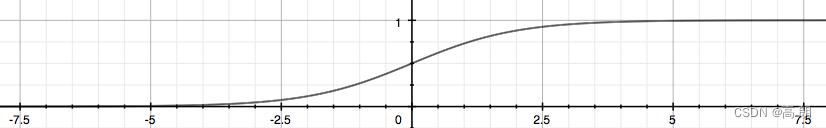
Sigmoid函数是一个S型的函数,当自变量z趋近正无穷时,因变量g(z)趋近于1,而当z趋近负无穷时,g(z)趋近于0,它能够将任何实数映射到(0,1)区间,使其可用于将任意值函数转换为更适合二分类的函数。
二元逻辑回归的一般形式:
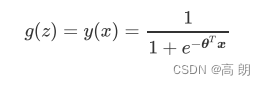
逻辑回归,可以理解维为由线性回归通过Sigmoid函数转换,使其预测值在[0,1]之间,达到二分类的效果。
为什么叫逻辑回归?何来的逻辑?
y ( x ) y(x) y(x)是逻辑回归返回的标签值,且取值在[0,1]之间,所以 y ( x ) y(x) y(x)和 1 − y ( x ) 1-y(x) 1−y(x)的和必然是1,如
果我们令 y ( x ) y(x) y(x) 除以 1 − y ( x ) 1-y(x) 1−y(x)可以得到形似几率(odds)的 y ( x ) 1 − y ( x ) \frac{y(x)}{1-y(x)} 1−y(x)y(x) ,在此基础上取对数,可以很容易就得到:
y(x)的形似几率取对数的本质其实就是我们的线性回归z,我们实际上是在对线性回归模型的预测结果取
对数几率来让其的结果无限逼近0和1。因此,其对应的模型被称为”对数几率回归“(logistic Regression),音译过来就是逻辑回归,这个名为“回归”却是用来做分类工作的分类器。
定义损失函数
定义损失函数非常重要,它能帮我们找到一组最佳的参数θ和偏置b,使得我们的模型能够更加准确的进行预测,即是说,能够衡量参数的模型拟合训练集时产生的信息损失的大小,并以此衡量参数的优劣,我们在求解参数时,追求损失函数最小,让模型在训练数据上的拟合效果最优。
二元逻辑回归的标签服从伯努利分布(即0-1分布):
我们可以将一个特征向量为x,参数为θ的模型中的一个样本i的预测情况表现为如下形式:
- 样本i在由特征向量x和参数θ组成的预测函数中,样本标签被预测为1的概率为:
- 样本i在由特征向量x和参数θ组成的预测函数中,样本标签被预测为0的概率为:
当 P 1 P_1 P1被的值为1的时候,代表样本i的标签被预测为1,当 P 0 P_0 P0的值为1的时候,代表样本i的标签被预测为0。
样本
i的真实标签 y i y_i yi为1:
- 如果 P 1 P_1 P1为1, P 0 P_0 P0为0,就代表样本
i的标签被预测为1,与真实值一致。模型预测正确没有信息损失。- 如果 P 1 P_1 P1此时为0, P 0 P_0 P0为1,就代表样本
i的标签被预测为0,与真实情况完全相反。预测错误有损失信息。
同理真实值 y i y_i yi为0的情况,所以希望当 y i y_i yi为1的时候,我们希望 P 1 P_1 P1非常接近1,当 y i y_i yi为0的时候,我们希望 P 0 P_0 P0非常接近1,这样,模型的效果就很好,信息损失就很少。
将两种取值的概率整合,我们可以定义如下等式:
y i ^ 预测值 \hat{y_i}预测值 yi^预测值,当预测值与真实值一样时,上式是1的,表示预测真确,所以我们在追求 P ( y i ^ ∣ x i , θ ) P(\hat{y_i}|x_i,θ) P(yi^∣xi,θ)的最大值。这就将模型拟合中的“最小化损失”问题,转换成了对函数求解极值的问题。
P ( y i ^ ∣ x i , θ ) P(\hat{y_i}|x_i,θ) P(yi^∣xi,θ)是对单个样本i而言的函数,对一个训练集的m个样本来说,我们可以定义如下等式来表达所有样本在特征矩阵X和参数θ组成的预测函数中,预测出所有可能的 y ^ \hat{y} y^的概率P为:
这就是我们的交叉熵函数。为了数学上的便利以及更好地定义”损失”的含义,我们希望将极大值问题转换为极小值问题,因此我们对 log P \log{P} logP取负,并且让参数θ作为函数的自变量,就得到了我们的损失函数:
这就是一个,基于逻辑回归的返回值 y θ ( x i ) y_θ(x_i) yθ(xi)的概率性质得出的损失函数。在这个函数上,我们只要追求最小值,就能让模型在训练数据上的拟合效果最好,损失最低。
正则化
正则化是用来防止模型过拟合的过程,常用的有L1正则化和L2正则化两种选项,分别通过在损失函数后加上参数向量 的L1范式和L2范式的倍数来实现。
这个增加的范式,被称为“正则项”,也被称为"惩罚项"。损失函数改变,基于损失函数的最优化来求解的参数取值必然改变,我们以此来调节模型拟合的程度。
L1范数:Loss function 加上 参数的绝对值之和,可以起到一个特征筛选的作用,使得某些参数直接为0。
L2范数:Loss function 加上 参数的绝对值平方之和,可以使Loss function更加平缓,防止出现过拟合,但只能使参数接近于0,不能为0,不能特征筛选。
sklearn里面的逻辑回归
- 类:
linear_model.LogisticRegression - 参数:




- 属性

- 接口

参数很多,但只需要理解下面常用的即可:
- 正则化相关
| 参数 | 说明 |
|---|---|
| penalty | 可以输入"l1"或"l2"来指定使用哪一种正则化方式,不填写默认"l2"。 注意,若选择"l1"正则化,参数solver仅能够使用求解方式”liblinear"和"saga“,若使用“l2”正则化,参数solver中所有的求解方式都可以使用。 |
| C | C正则化强度的倒数,必须是一个大于0的浮点数,不填写默认1.0,即默认正则项与损失函数的比值是1:1。C越小,损失函数会越小,模型对损失函数的惩罚越重,正则化的效力越强,参数会逐渐被压缩得越来越小。 |
sklearn里面L1和L2的公式:
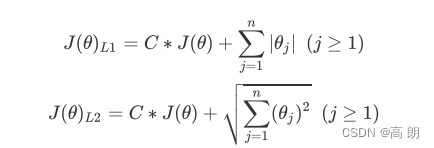
导入库:
from sklearn.linear_model import LogisticRegression as LR # 逻辑回归
from sklearn.datasets import load_breast_cancer # 乳腺癌数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split # 划分测试集和训练集
from sklearn.metrics import accuracy_score # 精确性,模型评估指标之一
data = load_breast_cancer() # 数据集
X = data.data # 特征
y = data.target # 标签lrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000) # L1范数
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000) # L2范数lrl1 = lrl1.fit(X,y)
lrl2 = lrl2.fit(X,y)通过coef_属性,查看每个特征所对应的参数:
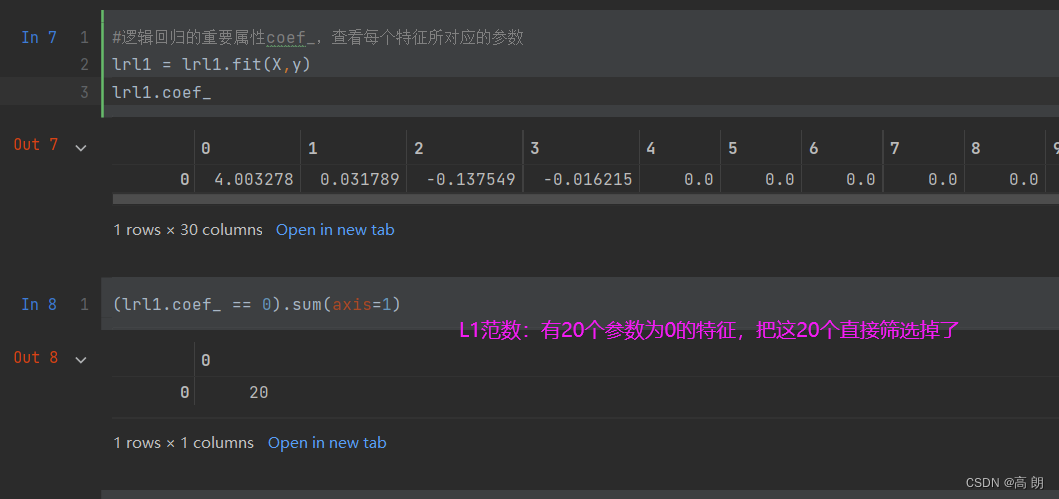
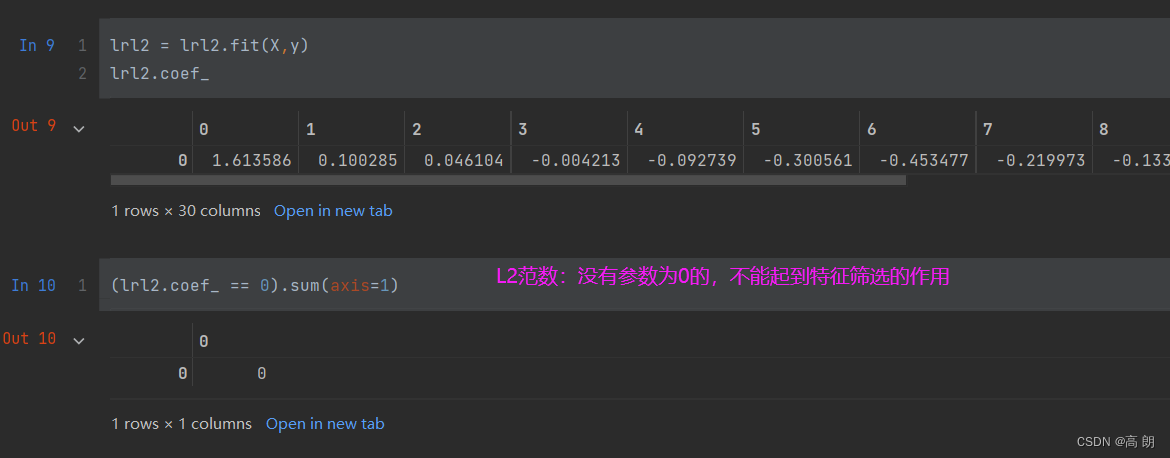
L1和L2模型训练的效果比较:
l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.linspace(0.05,1,19):lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)lrl1 = lrl1.fit(Xtrain,Ytrain)l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))lrl2 = lrl2.fit(Xtrain,Ytrain)l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示,右下角
plt.show()
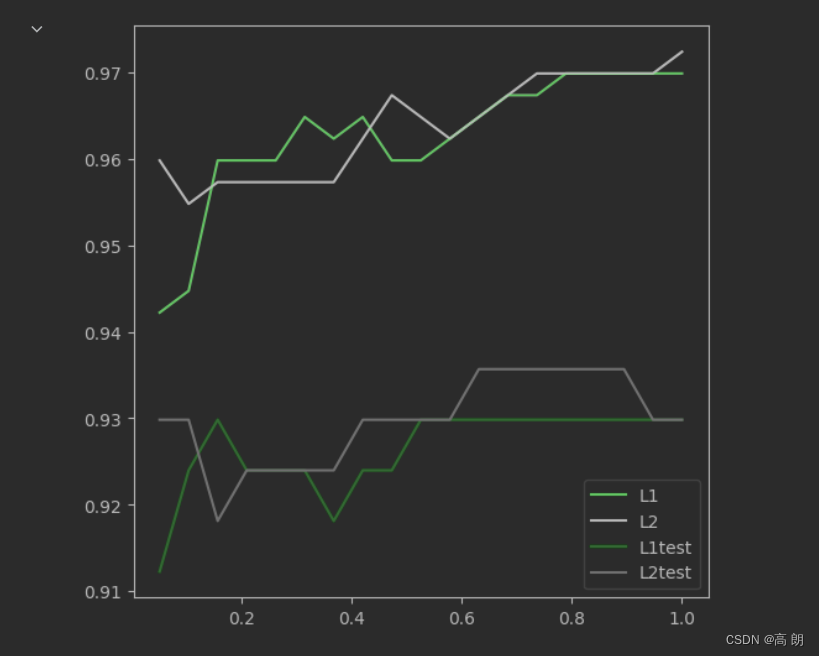 两种正则化的结果区别不大。但随着C的逐渐变大,正则化的强度越来越小,模型在训练集和测试集上的表现都呈上升趋势,直到C=0.8左右,训练集上的表现依然在走高,但模型在未知数据集上的表现开始下跌,这时候就是出现了过拟合。我们可以认为,C设定为0.8会比较好。在实际使用时,基本
两种正则化的结果区别不大。但随着C的逐渐变大,正则化的强度越来越小,模型在训练集和测试集上的表现都呈上升趋势,直到C=0.8左右,训练集上的表现依然在走高,但模型在未知数据集上的表现开始下跌,这时候就是出现了过拟合。我们可以认为,C设定为0.8会比较好。在实际使用时,基本
就默认使用l2正则化,如果感觉到模型的效果不好,那就换L1试试看。
- 重要参数
max_iter:最大的迭代次数【进行梯度下降找最小值的迭代次数】
参数max_iter最大迭代次数来代替步长(lreaning rate),帮助我们控制模型的迭代速度并适时地让模型停下。max_iter越大,代表步长越小,模型迭代时间越长,反之,则代表步长设置很大,模型迭代时间很短。
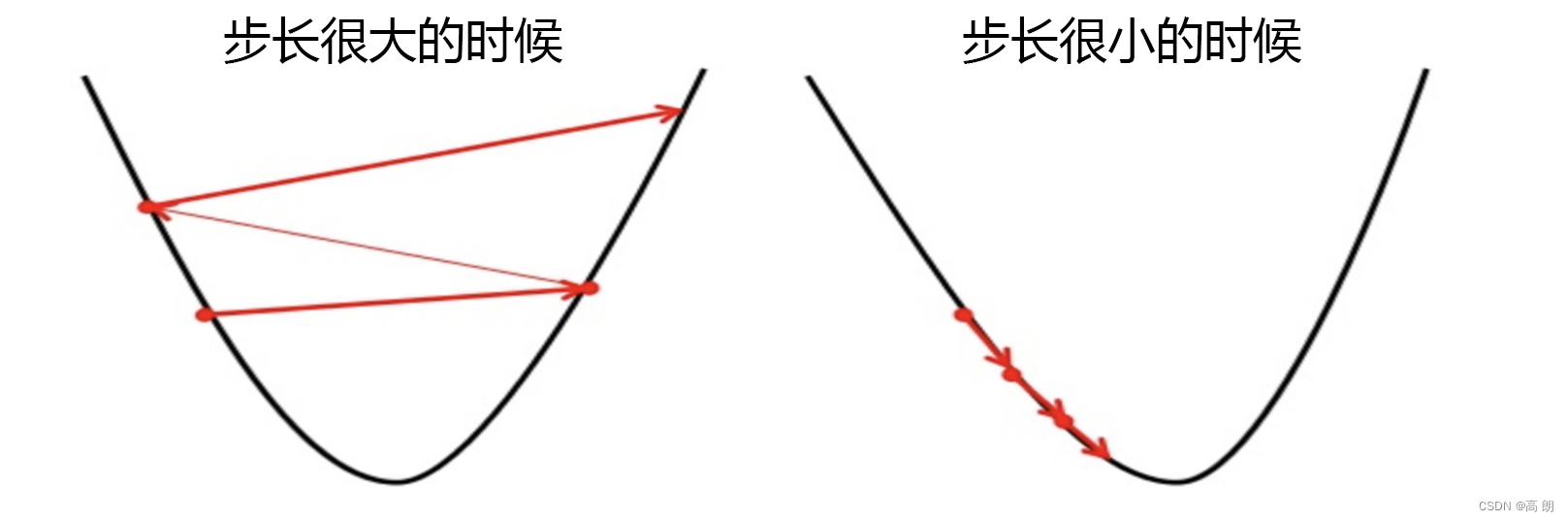
来看看乳腺癌数据集下,max_iter的学习曲线:
循环迭代次数
l2 = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.arange(1,201,10):lrl2 = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=i)lrl2 = lrl2.fit(Xtrain,Ytrain)l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
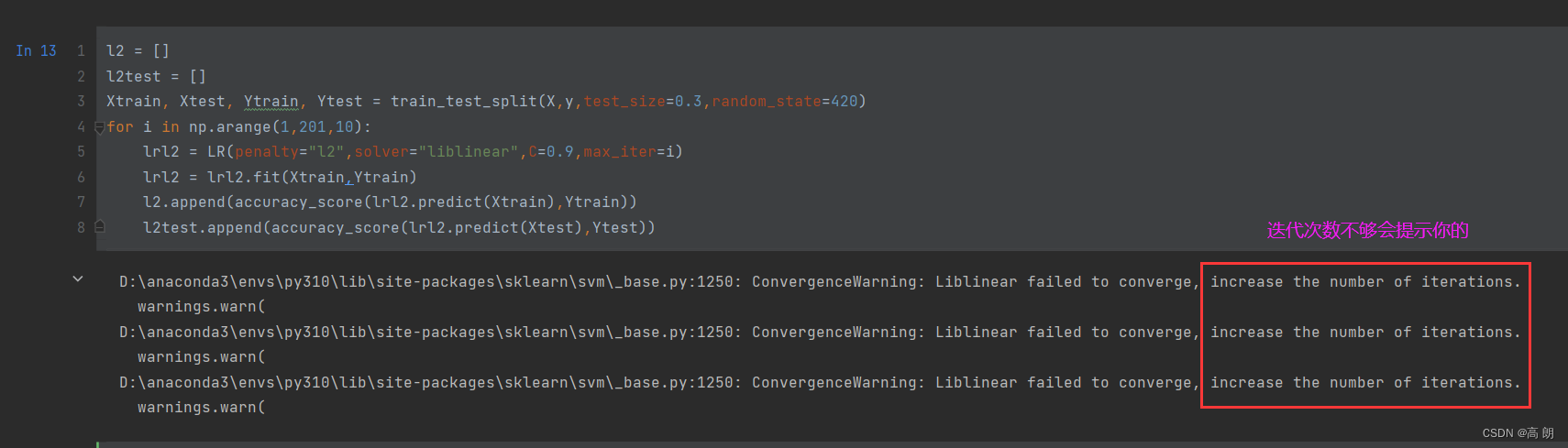
画出迭代次数与准确率的图
graph = [l2,l2test]
color = ["black","gray"]
label = ["L2","L2test"]plt.figure(figsize=(20,5))
for i in range(len(graph)):plt.plot(np.arange(1,201,10),graph[i],color[i],label=label[i])plt.legend(loc=4)
plt.xticks(np.arange(1,201,10))
plt.show()
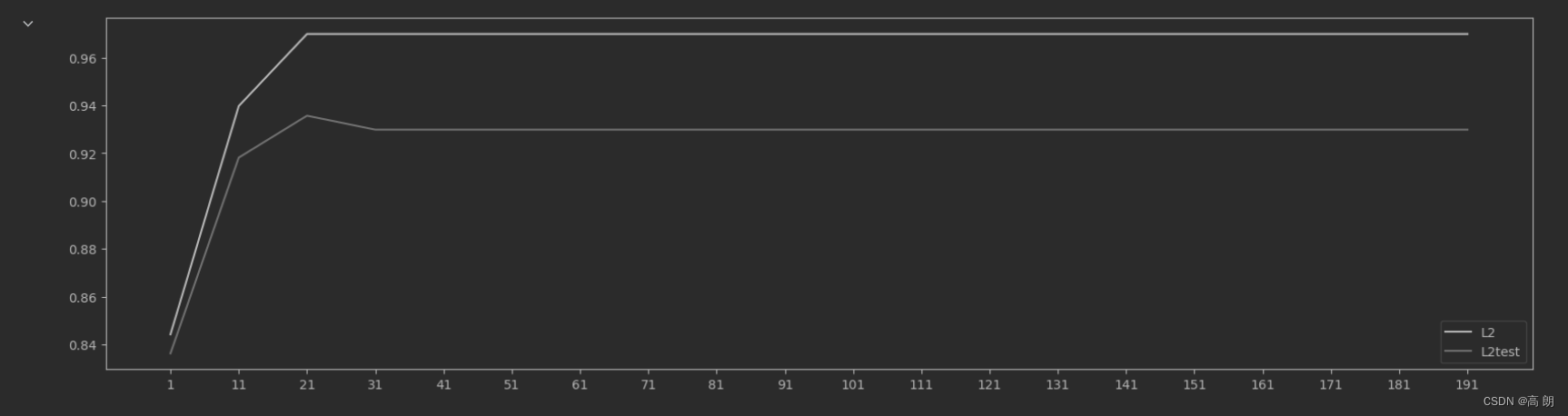
#我们可以使用属性.n_iter_来调用本次求解中真正实现的迭代次数
lr = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=300).fit(Xtrain,Ytrain)
lr.n_iter_
最大的迭代次数,并不是说就会迭代这么多次,如果梯度下降找到了局部最优点就会停止:

- 重要参数
solver&multi_class:【二元回归与多元回归】
上面都是针对二分类的逻辑回归展开,其实sklearn提供了多种可以使用逻辑回归处理多分类问题的选项。比如说,我们可以把某种分类类型都看作1,其余的分类类型都为0值,和”数据预处理“中的二值化的思维类似,这种方法被称为"一对多"(One-vs-rest),简称OvR,在sklearn中表示为“ovr"。又或者,我们可以把好几个分类类型划为1,剩下的几个分类类型划为0值,这是一种”多对多“(Many-vs-Many)的方法,简称MvM,在sklearn中表示为"Multinominal"。每种方式都配合L1或L2正则项来使用。
在sklearn中,我们使用参数multi_class来告诉模型,我们的预测标签是什么样的类型。
- “
auto”:表示会根据数据的分类情况和其他参数来确定模型要处理的分类问题的类型。比如说,如果数据是二分类,或者solver的取值为"liblinear",“auto"会默认选择"ovr”。反之,则会选择"nultinomial"。【默认】 - “
ovr”:表示分类问题是二分类,或让模型使用"一对多"的形式来处理多分类问题。 - ‘
multinomial’:表示处理多分类问题,这种输入在参数solver是’liblinear’时不可用。
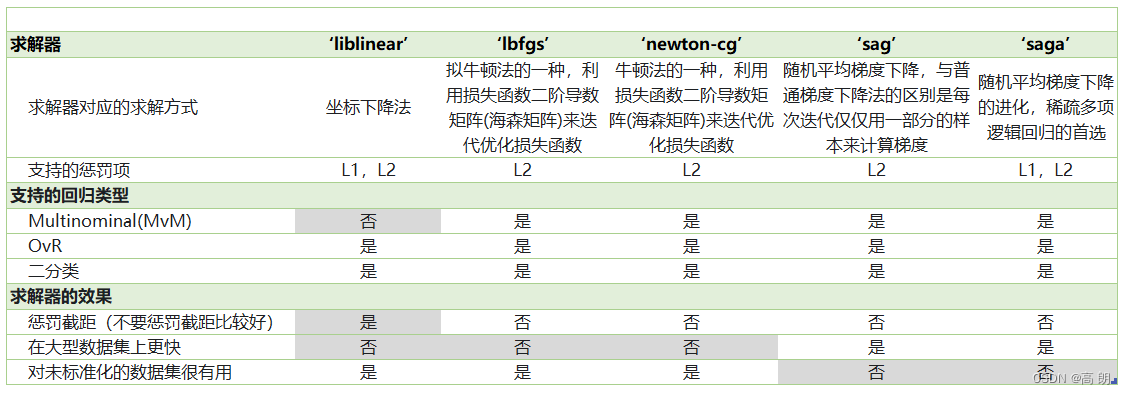
multinomial和ovr的区别:【鸢尾花数据集】
from sklearn.datasets import load_iris
iris = load_iris()
for multi_class in ('multinomial', 'ovr'):clf = LR(solver='sag', max_iter=200, random_state=42,multi_class=multi_class).fit(iris.data, iris.target)
#打印两种multi_class模式下的训练分数
#%的用法,用%来代替打印的字符串中,想由变量替换的部分。%.3f表示,保留三位小数的浮点数。%s表示,字符串。
#字符串后的%后使用元祖来容纳变量,字符串中有几个%,元祖中就需要有几个变量print("training score : %.3f (%s)" % (clf.score(iris.data, iris.target), multi_class))
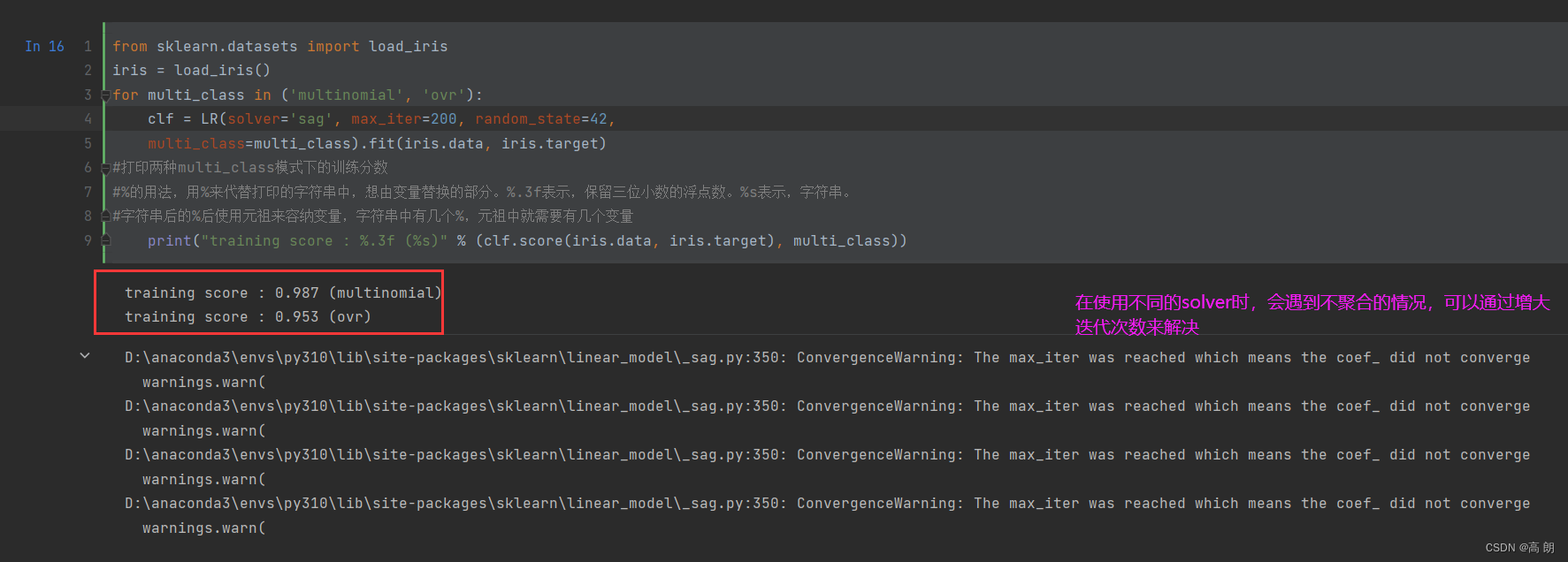
多项式逻辑回归
上文逻辑回归是在平面上找一条直线,用这条直线来分割所有样本对应的分类。
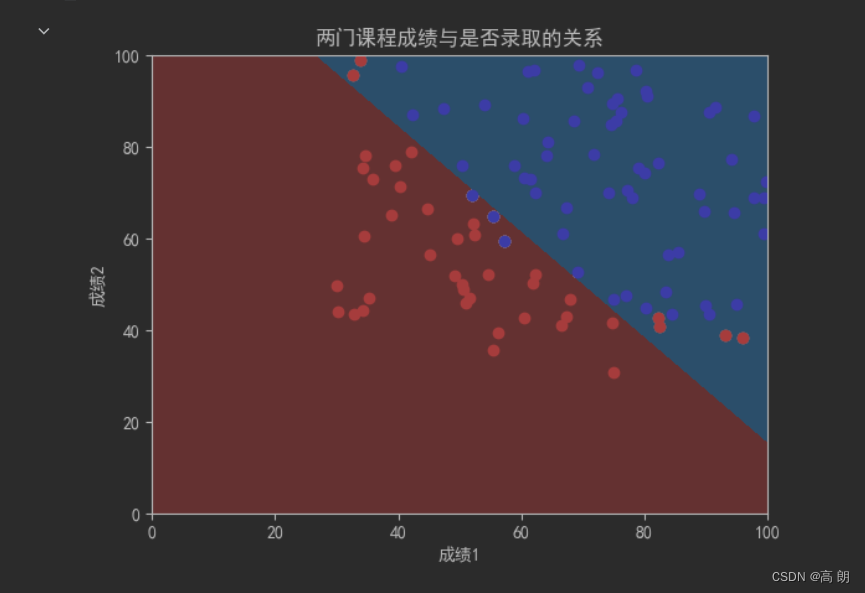 从图片中可以看得,一条直线不可能将红蓝点完全分隔开,可以采用多项式,不使用直线来分割,尽可能的提高分类的准确率。
从图片中可以看得,一条直线不可能将红蓝点完全分隔开,可以采用多项式,不使用直线来分割,尽可能的提高分类的准确率。
多项式实现:
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
#专门产生多项式的,并且多项式包含的是相互影响的特征集。
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split#增加多项式预处理
def polynomial_model(degree=1,**kwarg):polynomial_features = PolynomialFeatures(degree=degree,include_bias=False)logistic_regression = LogisticRegression(solver='liblinear',**kwarg)#solver的默认参数是'lbfgs',只支持L2,要改成'liblinear',L1,L2都能支持pipeline = Pipeline([("polynomial_features",polynomial_features),("logistic_regression",logistic_regression)])return pipelineX_train, X_test, y_train, y_test = train_test_split(data_X, data_y, random_state=666)
#增加二阶多项式特征,创建并训练模型
model=polynomial_model(degree=2,penalty='l1',max_iter=1000)#使用L1范式作为正则项,进行稀疏化
model.fit(X_train,y_train)#训练模型
# 结果可视化
plot_decision_boundary(model, axis=[0, 100, 0, 100])
plt.scatter(data_X[data_y == 0, 0], data_X[data_y == 0, 1], color='red')
plt.scatter(data_X[data_y == 1, 0], data_X[data_y == 1, 1], color='blue')
plt.xlabel('成绩1')
plt.ylabel('成绩2')
plt.title('两门课程成绩与是否录取的关系')
plt.show()
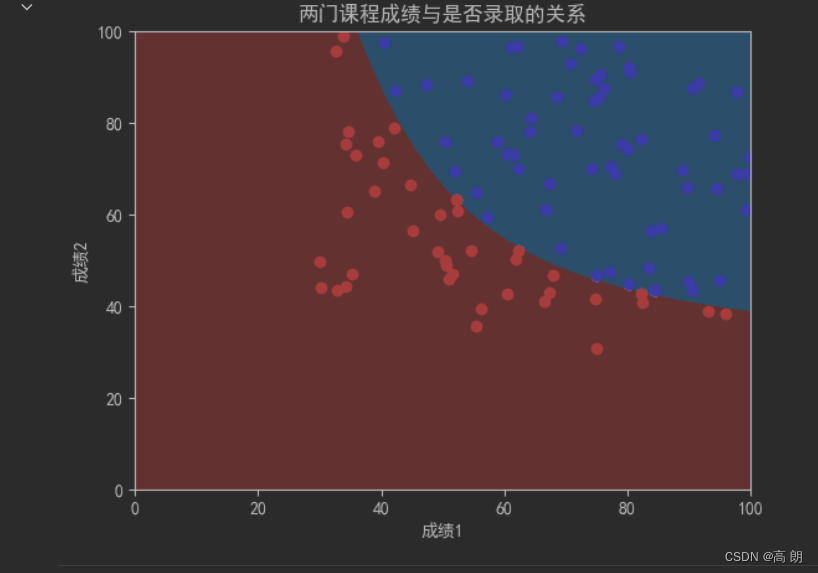 从图片中可以看到采用多项式之后,基本能够完全分隔开红蓝两类,至少准确率要比之前的高。
从图片中可以看到采用多项式之后,基本能够完全分隔开红蓝两类,至少准确率要比之前的高。
相关文章:

【机器学习】逻辑回归
文章目录 逻辑回归定义损失函数正则化 sklearn里面的逻辑回归多项式逻辑回归 逻辑回归 逻辑回归,是一种名为“回归”的线性分类器,其本质是由线性回归变化而来的,一种广泛使用于分类问题中的广义回归算法。 线性回归是机器学习中最简单的的…...

DITA-OT 4.0新特性 - PDF themes,定制PDF样式的新方法
随着DITA-OT 4.0的发布,它提供了一种新的定制PDF样式方法,这种方法就是PDF theme。这篇文章来聊一聊这种定制PDF输出的新方法和实验结果。 在进入PDF theme细节之前,为各位读者梳理一下DITA-OT将DITA和Markdown发布成PDF的几种方法。 - 1 …...

MySQL 8.0 OCP认证精讲视频、环境和题库之四 多实例启动 缓存、事务、脏读
一、配置第一个mysqld服务 1、编辑选项文件,指定以下选项: [mysqld] basedir/mysql80 datadir/mysql80/data1 socket/mysql80/data1/mysqld.sock pid-file/mysql80/data1/mysqld.pid log-error/mysql80/dat…...
对代码感兴趣 但不擅长数学怎么办——《机器学习图解》来救你
目前,该领域中将理论与实践相结合、通俗易懂的著作较少。机器学习是人工智能的一部分,很多初学者往往把机器学习和深度学习作为人工智能入门的突破口,非科班出身的人士更是如此。当前,国内纵向复合型人才和横向复合型人才奇缺;具有…...

【EI会议征稿】第三届大数据、信息与计算机网络国际学术会议(BDICN 2024)
第三届大数据、信息与计算机网络国际学术会议(BDICN 2024) 2024 3rd International Conference on Big Data, Information and Computer Network 第三届大数据、信息与计算机网络国际学术会议(BDICN 2024)定于2024年1月12-14日在…...
【Arduino+ESP32+腾讯云+sg90】强制门户+腾讯云控制开关灯
作者有话说 博主对于Arduino开发并没有基础,但是为了实现更加方便的配网,这几天一直在尝试用ESP32-12F(因为手头刚好有一个,其他的也可以)来做远程开关灯!不知道大家是否注意到,上一篇利用STM32…...
windows中elasticsearch7中添加用户名密码验证
1.找到elsatic的bin目录输入cmd 2.生成ca证书 输入 elasticsearch-certutil ca 在es7根目录生成ca证书,输入密码时直接回车即可,否则后面会报错 Please enter the desired output file [elastic-stack-ca.p12]: #这里直接回车即可 Enter password for…...

linux安装达梦数据库(命令行安装)
安装达梦数据库 创建安装用户 1,创建安装用户组dinstall [rootdmDMServer1 ~]# groupadd -g 12345 dinstallgroupadd : 创建组 -g : 指定组id(GID) 12345: 指定的组名称 dinstall : 组名 2,创建安装用户dmdba [rootdmDMSe…...

Flutter——最详细(CustomScrollView)使用教程
CustomScrollView简介 创建一个 [ScrollView],该视图使用薄片创建自定义滚动效果。 [SliverList],这是一个显示线性子项列表的银子列表。 [SliverFixedExtentList],这是一种更高效的薄片,它显示沿滚动轴具有相同范围的子级的线性列…...

解决容器内deepspeed微调大模型报错
解决容器内deepspeed微调大模型报错:[launch.py:315:sigkill_handler] Killing subprocess 问题描述:解决办法 问题描述: 在容器中用deepspeed微调百川大模型2时,出现上述错误,错误是由于生成容器时,共享内…...
UE 插件模块引用
如Plugons中的模块A想要引用模块B: 1、模块A中的.uplugin文件加入↓ 2、模块A中的.Build.cs文件加入↓ 3、在模块A需要用到模块B的地方直接include 4、重新generate Project 5、重新编译 注意两个模块之间不能循环引用...

python元组、拆包和装包
注意 元组不能修改元素 元组:如果元素为字符串且元素为1个,必须加一个, ********* t1 (aa,) 下标和切片 in not in for ... in ... 元组转为列表 拆包、装包...

1-Docker安装MySQL8.0
1 背景知识记录 1.1 MySQL 的基本配置记录 MySQL的配置文件目录(/etc/mysql): root2dd6033b5c17:/etc/mysql# pwd /etc/mysql root2dd6033b5c17:/etc/mysql# ls conf.d my.cnf my.cnf.fallback MySQL的data文件目录(/var/lib/my…...

配电房智能化改造在加油站等的应用
随着科技的发展和智能化趋势的推进,对加油站配电房进行智能化改造成为了一个必然的选择。智能化改造不仅可以提高加油站的工作效率,减少事故发生率,还可以实现能源的合理利用,提高经济效益。 力安科技加油站智能化改造升级是一种高…...
)
集准测试-架构真题(五十六)
如果数据库单标即可实现业务功能,采用()方式进行数据交换与处理较为合适。如果通过数据库不同表的连接操作获取数据才能实现业务功能,这时候采用()方式进行数据交换与处理合适。 主动记录数据网关包装器数…...

木与空间的舞蹈:奥地利住宅的独特设计
国外著名设计师,为一位业主设计了一座住宅,附带有附属建筑和有盖的入口,形成了像庭院一样的建筑群。 这座住宅采用了当地的传统建筑风格,有长方形的平面和陡峭的顶棚,与周围的房屋相符。然而,内部设计别具一…...
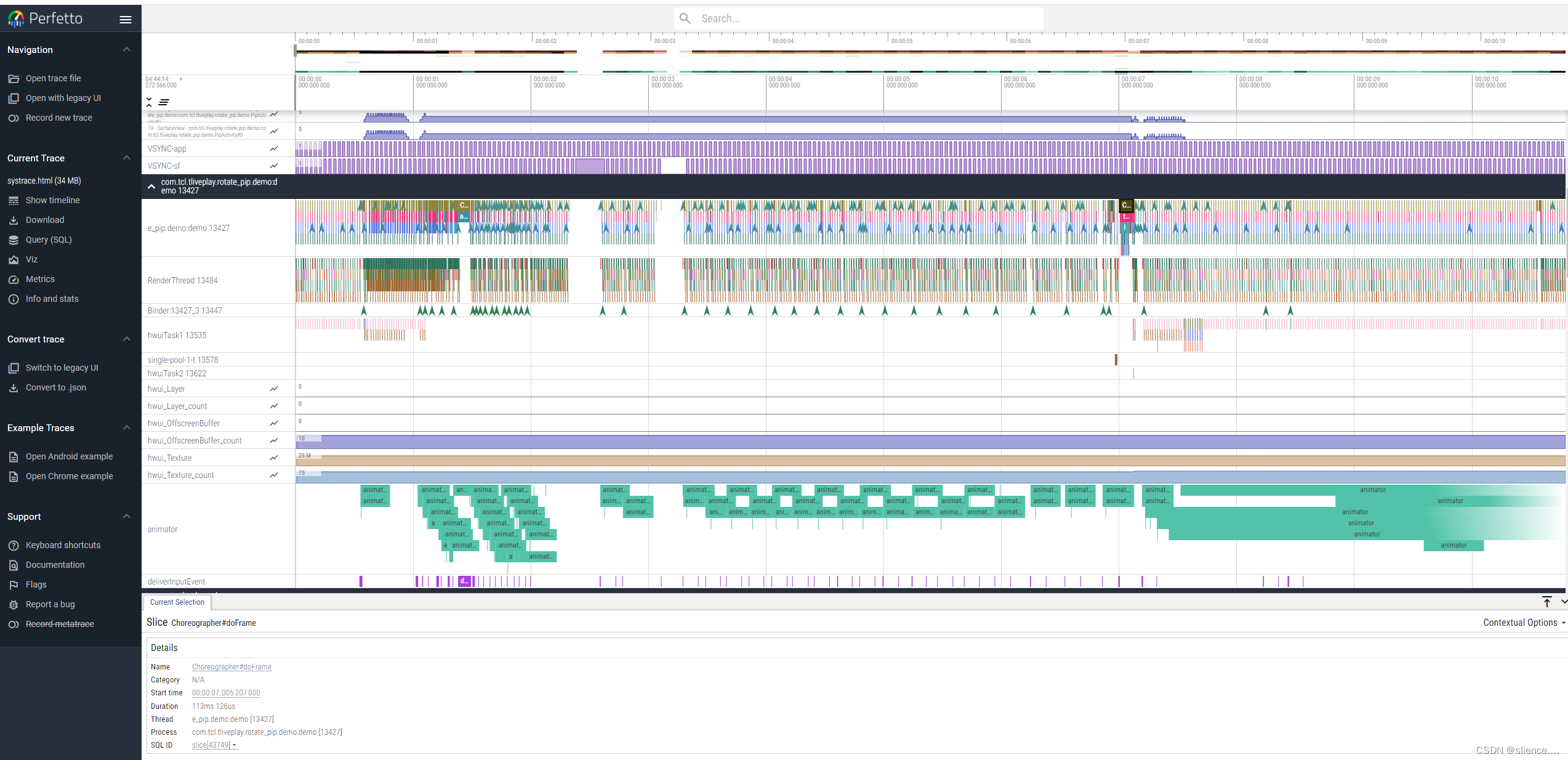
性能优化-卡顿优化-tarce抓取及分析
性能优化(卡顿分析) 文章目录 一、抓取trace的方法1.使用systrace抓取trace2.使用atrace抓取3.使用Perfetto抓取trace 二、trace文件的分析1.快捷操作1.1 导航操作1.2 快捷操作 2.chrome trace工具分析trace文件3.Prefetto分析trace文件 一、抓取trace的…...

P5740 【深基7.例9】最厉害的学生
题目描述 现有 N N N 名同学参加了期末考试,并且获得了每名同学的信息:姓名(不超过 8 8 8 个字符的仅有英文小写字母的字符串)、语文、数学、英语成绩(均为不超过 150 150 150 的自然数)。总分最高的学…...

Hive引擎MR、Tez、Spark
Hive引擎包括:默认MR、Tez、Spark 不更换引擎hive默认的就是MR。 MapReduce:是一种编程模型,用于大规模数据集(大于1TB)的并行运算。 Hive on Spark:Hive既作为存储元数据又负责SQL的解析优化࿰…...

不写前端代码,curl直接调试sse
不写前端代码,curl直接开两个终端调试sse 过程: 客户端向服务端发送建立连接请求; 服务端向客户端推送内容; 服务端向客户端发送结束信号并结束 注意事项: 只有连接时要求content-type是xxx 其他问题: …...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...