一起学数据结构(9)——二叉树的链式存储及相关功能实现
目录
1. 二叉树的链式存储:
2. 二叉树的前序遍历:
3. 二叉树的中序遍历:
4. 二叉树的后序遍历:
5. 统计二叉树的结点总数
6.统计二叉树的叶子结点数:
7. 统计二叉树第层的结点数量:
8. 二叉树的销毁:
9.查找树中值为结点:
10. 二叉树的层序遍历:
11. 代码总览:
11.1 头文件TRLIst.h
11.2 函数实现文件TRList.c
11.3 函数测试文件Test.c
在数据结构的第七篇文章中提到,对于完全二叉树而言,可以采用顺序存储的方法来存储完全二叉树。但是对于非完全二叉树而言,(例如下图中给出的二叉树)存储方法需要采用链式存储。本文将围绕二叉树的链式存储展开,介绍链式存储方法以及此类二叉树相关功能的实现。

1. 二叉树的链式存储:
在前几篇文章介绍完全二叉树及堆的代码实现时,会涉及到此类数据结构的插入结点、删除结点等特点。但是,对于非完全二叉树,由于结构并不像完全二叉树一样有一定规律,因此,利用非完全二叉树存储数据的操作较为复杂。并且,在存储数据这一方面,之前的完全二叉树更为合适。所以,对于普通的非完全二叉树来说,插入、删除结点的操作是没有意义的。
对于非完全二叉树的价值,主要是体现于后续更复杂的数据结构中,例如红黑树等。因此,文章后续实现的功能主要是利用递归来针对于非完全二叉树自身而言,例如求非完全二叉树的叶子结点数目,二叉树的深度等等。在二叉树的链式存储这一部分,将通过构建关于新建结点函数来手动构建上图给出的非完全二叉树。
对于非完全二叉树,在关于树的基础的文章中就提到,链式存储的方法可以归结为左孩子,右兄弟。所以,树的结点的结构如下:
typedef int TRDataType;
typedef struct TreeNode
{TRDataType val;struct TreeNode* left;struct TreeNode* right;
}TRNode; 在确立了二叉树结点的结构之后,下一步构建函数,代码如下:
TRNode* BuyTRNode(int x)
{TRNode* newnode = (TRNode*)malloc(sizeof(TRNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->val = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}下一步,通过上面的两个函数,直接构建出上图中给出的非完全二叉树,即:
int main()
{TRNode* node1 = BuyTRNode(1);TRNode* node2 = BuyTRNode(2);TRNode* node3 = BuyTRNode(3);TRNode* node4 = BuyTRNode(4);TRNode* node5 = BuyTRNode(5);TRNode* node6 = BuyTRNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return 0;
}(注: 文章后续所有的运行结果均需要适配相应的测试代码,测试代码将在文章最后统一给出)
2. 二叉树的前序遍历:
对于二叉树的前序遍历,其顺序是按照:根结点,左结点,右结点进行访问的,例如对于上面给出的树:其结点访问顺序依次为(注:将空看作结点):1,2,3,
,
,
,4,5,
,
,6,
,
。

利用图形来表示结点访问的顺序,即:
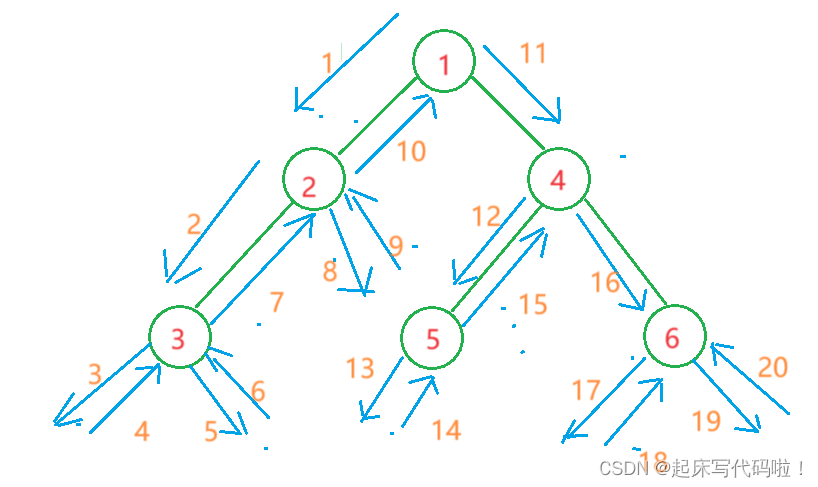
其中均代表访问到空结点,
代表访问到空结点后,返回上一个结点。在结点访问的过程中,每个结点都是按照:根结点、左结点、右结点的顺序。因此,对于这种重复性的问题,可以使用递归实现,具体代码如下:
//前序遍历
void PreOrder(TRNode* root)
{if (root == NULL){return;}//访问根结点:printf("%d ", root->val);//访问左结点:PreOrder(root->left);//访问右结点:PreOrder(root->right);
}运行结果如下:

3. 二叉树的中序遍历:
二叉树的中序遍历顺序为:左结点、根结点、右结点,依旧针对于上面给出的二叉树,中序遍历对于结点的访问顺序为:,3,
,2,
,1,
,5,
,4,
,6
。用图片表示结点的访问顺序,即:
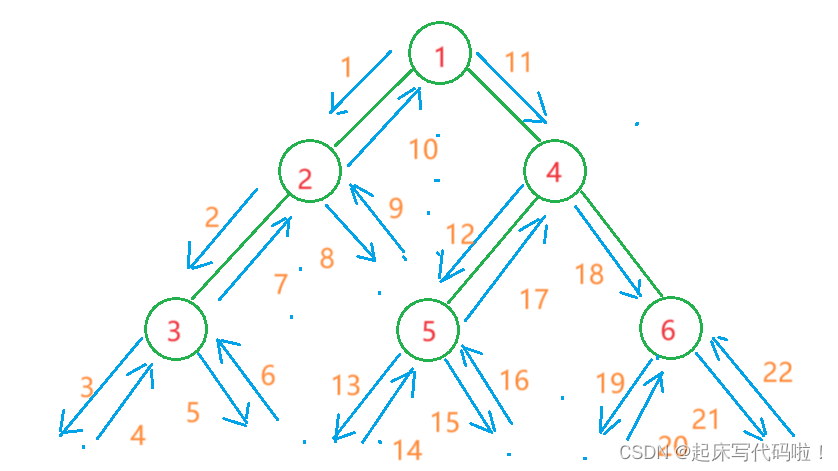
对应代码如下:
//中序遍历
void InOrder(TRNode* root)
{if (root == NULL){return;}//访问左结点:InOrder(root->left);//访问根结点:printf("%d ", root->val);//访问右结点:InOrder(root->right);
}结果如下:

4. 二叉树的后序遍历:
二叉树的后序遍历顺序为:左结点,右结点,根结点。针对上方给出的二叉树,后序遍历访问结点的顺序依次为:,
,
,
,
,
,
,
,
,
,
,
,
。
用图形表示结点的访问顺序,即:
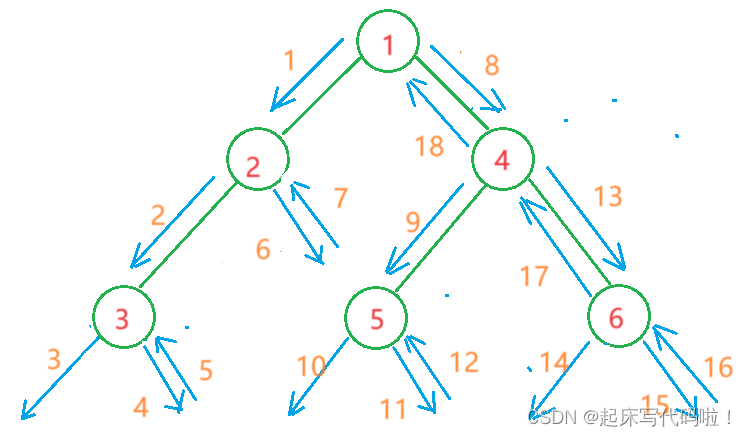
对应代码如下:
//后序遍历
void PostOrder(TRNode* root)
{if (root == NULL){return;}//访问左结点:InOrder(root->left);//访问右结点:InOrder(root->right);//访问根结点:printf("%d ", root->val);}结果如下:

5. 统计二叉树的结点总数
对于统计二叉树的结点总数这一功能,可以拆分为以下步骤利用递归进行实现:
1. 检测结点是否为空,如果为空,则表示结点为空,即不存在此结点,返回。如果不为空,则表示存在本结点,结果加1并且向下检测本结点的左、右结点。
2.在检测结点时,需要检测结点的左、右结点,检测方法参考1
具体代码如下:
//统计二叉树的结点树:
int TreeSize(TRNode* root)
{if (root == NULL){return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}测试结果如下:
6.统计二叉树的叶子结点数:
对于统计二叉树叶子结点数的功能实现,可以分成下面的部分:
1. 检测本结点是否符合叶子结点的特点,即:,并且
。如果符合,则返回值返回
。
2.若本结点不符合1中的判定条件,则存在两种情况,一是本结点为空,二是本结点为分支结点。对于第一种情况,返回值返回,对于第二种情况,则继续向下检测本结点的子结点,即
对应代码为:
//统计二叉树的叶子结点数:
int TreeLeafSize(TRNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}运行结果如下:
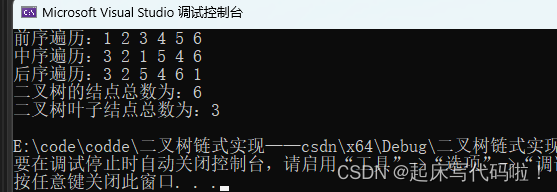
符合上图中的叶子结点数量。
7. 统计二叉树第 层的结点数量:
层的结点数量:
对于此功能的实现,同样可以分为下面的几步:
1.额外创建一个变量,用
来间接表示二叉树的层数,每经过依次递归,对
进行一次
的操作。当
时,表示已经到达目标层数。此时,如果目标层存在结点,则返回值返回
.
2.当时,表示还未到达目标层数,继续向下遍历该结点左、右两个子结点。
3.在函数传参的时候,需要注意,不能传递,需要传递
。具体代码如下:
//统计二叉树第k层结点数
int TNodeSize(TRNode* root, int k)
{if (root == NULL){return 0;}if (k == 0){return 1;}return TNodeSize(root->left, k - 1) + TNodeSize(root->right, k - 1);
}运行结果如下:

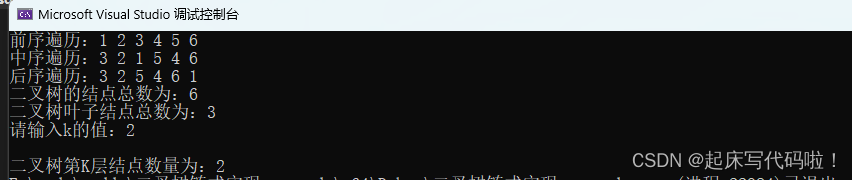


结点数量符合上方给出的二叉树。
8. 二叉树的销毁:
原理较为简单,只给出代码,不做过多解释:
//二叉树的销毁
void TNodeDestory(TRNode* root)
{if (root == NULL){return;}TNodeDestory(root->left);TNodeDestory(root->right);free(root);
}9.查找树中值为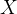 结点:
结点:
对于查找树中值为的结点这一功能,可以分成下面的步骤实现:
1. 检测本结点是否为空,如果为空则返回。
2.若本结点不为空,则检测本结点中存储的数值是否,若符合条件,则返回该结点的地址。
3.此时,结点即不为空,结点中存储的数值也,因此,继续遍历该结点的左、右两个子结点。
对于函数返回值的处理,可以在函数中额外创建一个函数指针,为了方便表达,将这个指针命名为。
如果函数的根结点中存储的数值就是,则直接返回该结点指针。如果不等于,按照上面的思路,函数会继续遍历根结点的子结点。直接令
接收函数的返回值,并且,在遍历的后方加上对于
的判定。由于
的返回值只存在两种情况,即
。所以,如果
返回值不为
,则不允许返回返回值。判定
的返回值为
,则返回返回值。如果在函数遍历的过程中,所有的
都不允许返回,则表示树种不存在存储数值为
的结点。直接返回
对应代码如下:
//查找树中值为x的结点:
TRNode* TRFind(TRNode* root,int x)
{if (root == NULL){return NULL;}if (root->val = x){return root;}TRNode* ret = NULL;ret = TRFind(root->left, x);if (ret){return ret;}ret = TRFind(root->right, x);if (ret){return ret;}return NULL;
}运行结果如下:
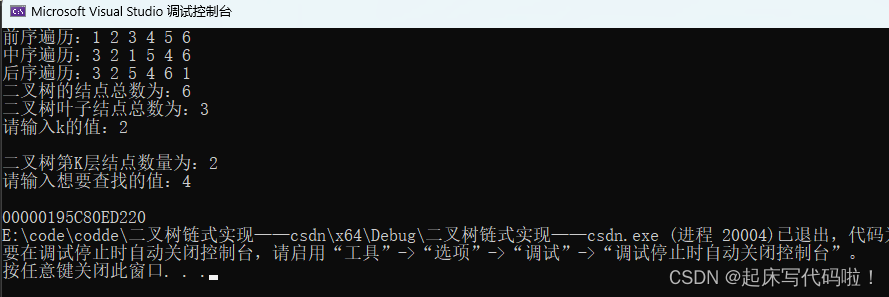
10. 二叉树的层序遍历:
对于二叉树的层序遍历,由于需要每一层挨个访问结点,因此,不能再用前面递归的思想来实现此功能 。如果不采用递归,则必须对每个结点的数值进行一次存储。所以,文章这里利用队列来辅助实现二叉树的层序遍历
(注:关于队列的相关知识及代码,可在前面的文章一起学数据结构(6)——栈和队列-CSDN博客获取,需要注意,在实现本功能时,需要将队列头文件中,
改成
以便匹配后序的返回值)
实现本功能的具体思路如下:
1. 创建一个队列,为了方便表达,将这个队列命名为。
2. 先往队列中利用插入函数插入二叉树根结点的数值。
3. 创建一个指针,命名为,利用这个指针来接受
函数(取队头元素函数)的返回值(返回值返回该结点的地址)。
4.按照层序遍历的顺序(即:一层一层,从左到右访问结点),向队列中插入数据,顺序为:插入左子结点,插入右子结点
5.销毁队头指针,利用循环配合上述步骤来完成对整个二叉树的访问,判定条件为(探空函数)
对应代码如下:
//层序遍历
void LevelOrder(Que* qs,TRNode* root)
{if(root)QueuePush(qs, root);while (!QueueEmpty(qs)){TRNode* violent = QueueFront(qs);printf("%d ", violent->val);if (violent->left)QueuePush(qs,violent->left);if (violent->right)QueuePush(qs,violent->right);QueuePop(qs);}}运行结果如下: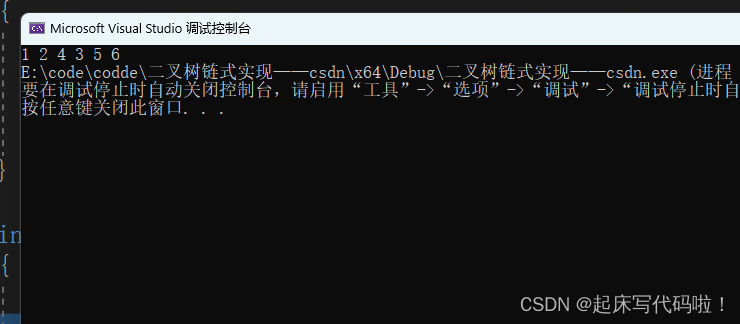
11. 代码总览:
11.1 头文件TRLIst.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>typedef int TRDataType;
typedef struct TreeNode
{TRDataType val;struct TreeNode* left;struct TreeNode* right;
}TRNode;#include"queue.h"//结点插入函数
TRNode* BuyTRNode(int x);//前序遍历
void PreOrder(TRNode* root);//中序遍历
void InOrder(TRNode* root);//后序遍历
void PostOrder(TRNode* root);//统计二叉树的结点树:
int TreeSize(TRNode* root);//统计二叉树的叶子结点数:
int TreeLeafSize(TRNode* root);//统计二叉树第k层结点数
int TNodeSize(TRNode* root, int k);//二叉树的销毁
void TNodeDestory(TRNode* root);//查找树中值为x的结点:
TRNode* TRFind(TRNode* root, int x);//层序遍历
void LevelOrder(Que* qs,TRNode* root);
11.2 函数实现文件TRList.c
#include"TRList.h"//结点插入函数
TRNode* BuyTRNode(int x)
{TRNode* newnode = (TRNode*)malloc(sizeof(TRNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->val = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}//前序遍历
void PreOrder(TRNode* root)
{if (root == NULL){return;}//访问根结点:printf("%d ", root->val);//访问左结点:PreOrder(root->left);//访问右结点:PreOrder(root->right);
}//中序遍历
void InOrder(TRNode* root)
{if (root == NULL){return;}//访问左结点:InOrder(root->left);//访问根结点:printf("%d ", root->val);//访问右结点:InOrder(root->right);
}//后序遍历
void PostOrder(TRNode* root)
{if (root == NULL){return;}//访问左结点:InOrder(root->left);//访问右结点:InOrder(root->right);//访问根结点:printf("%d ", root->val);
}//统计二叉树的结点树:
int TreeSize(TRNode* root)
{if (root == NULL){return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}//统计二叉树的叶子结点数:
int TreeLeafSize(TRNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}//统计二叉树第k层结点数
int TNodeSize(TRNode* root, int k)
{if (root == NULL){return 0;}if (k == 0){return 1;}return TNodeSize(root->left, k - 1) + TNodeSize(root->right, k - 1);
}//二叉树的销毁
void TNodeDestory(TRNode* root)
{if (root == NULL){return;}TNodeDestory(root->left);TNodeDestory(root->right);free(root);
}//查找树中值为x的结点:
TRNode* TRFind(TRNode* root,int x)
{if (root == NULL){return NULL;}if (root->val = x){return root;}TRNode* ret = NULL;ret = TRFind(root->left, x);if (ret){return ret;}ret = TRFind(root->right, x);if (ret){return ret;}return NULL;
}//层序遍历
void LevelOrder(Que* qs,TRNode* root)
{if(root)QueuePush(qs, root);while (!QueueEmpty(qs)){TRNode* violent = QueueFront(qs);printf("%d ", violent->val);if (violent->left)QueuePush(qs,violent->left);if (violent->right)QueuePush(qs,violent->right);QueuePop(qs);}}11.3 函数测试文件Test.c
#include"TRList.h"void TestOrder(TRNode* root)
{printf("前序遍历:");PreOrder(root);printf("\n");printf("中序遍历:");InOrder(root);printf("\n");printf("后序遍历:");PostOrder(root);printf("\n");
}void TestNode(TRNode* root)
{printf("二叉树的结点总数为:");int sum = TreeSize(root);printf("%d ", sum);printf("\n");int sum1 = TreeLeafSize(root);printf("二叉树叶子结点总数为:");printf("%d ", sum1);printf("\n");int k = 0;printf("请输入k的值:");scanf("%d", &k);int sum2 = TNodeSize(root, k-1);printf("\n");printf("二叉树第K层结点数量为:");printf("%d ", sum2);printf("\n");
}void TestTRDes(TRNode* root)
{printf("请输入想要查找的值:");int x = 0;scanf("%d", &x);TRNode* ret = NULL;ret = TRFind(root, x);printf("\n");
}void TestLOrder(TRNode* root)
{Que qs;QueueInit(&qs);LevelOrder(&qs, root);QueueDestory(&qs);
}int main()
{TRNode* node1 = BuyTRNode(1);TRNode* node2 = BuyTRNode(2);TRNode* node3 = BuyTRNode(3);TRNode* node4 = BuyTRNode(4);TRNode* node5 = BuyTRNode(5);TRNode* node6 = BuyTRNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;TestOrder(node1);TestNode(node1);TestTRDes(node1);TestLOrder(node1);return 0;
}相关文章:

一起学数据结构(9)——二叉树的链式存储及相关功能实现
目录 1. 二叉树的链式存储: 2. 二叉树的前序遍历: 3. 二叉树的中序遍历: 4. 二叉树的后序遍历: 5. 统计二叉树的结点总数 6.统计二叉树的叶子结点数: 7. 统计二叉树第层的结点数量: 8. 二叉树的销毁…...

vue 后端返回二进制流-前端通过blob对象下载文件-图片
前言 在实际开发中我们经常会遇见下载文件的场景,比如下载合同,下载文件 下载文件有2种方式,一种是后端返回二进制流,前端通过blob对象接受根据不同类型下载 还有一种把地址直接在浏览器新窗口打开浏览器打开pdf可以预览和下载&…...
)
vue el-dialog封装成子组件(组件化)
前言 实际开发过程中我们经常听见组件化开发,但在实际开发过程中(没有人审查时)怎么方便来 我们有时是因为时间不够,所以把所有代码写在一个页面。当业务逻辑复杂时可能会有1k多行 虽然不能要求自己写出高效复用性高的组件&…...

爬虫教程 一 requests包的使用
request 简介 requests 是一个常用的 HTTP 请求库,可以方便地向网站发送 HTTP 请求,并获取响应结果。 response.text 和response.content的区别 response.text 类型:str解码类型: requests模块自动根据HTTP 头部对响应的编码作…...
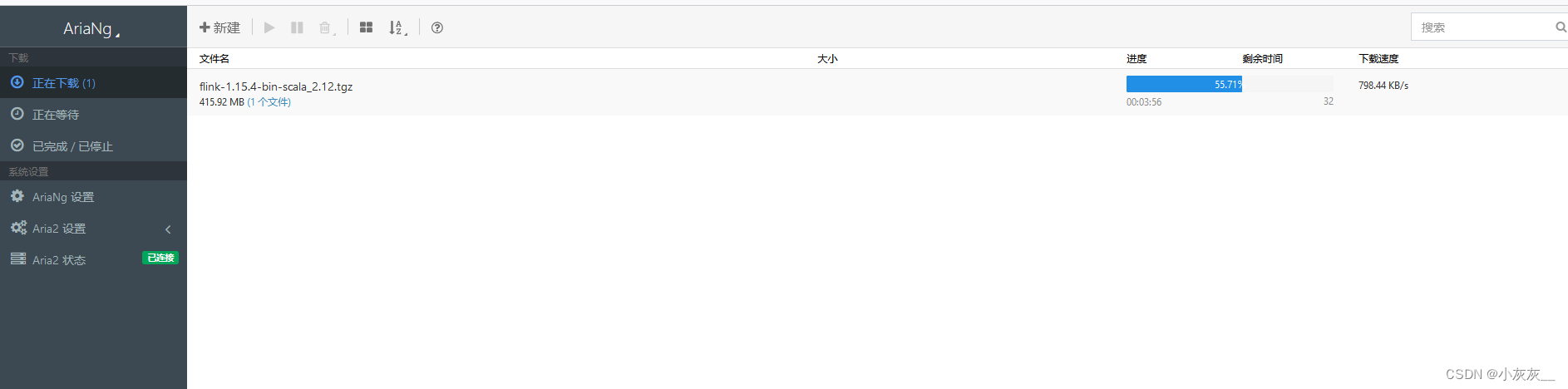
Aria2NG连接aria2-pro提示认证失败的处理办法
本文档适用于已经安装了aria2-pro和AriaNg的小伙伴~ 第一次登录管理端会提示”认证失败“ 这是因为aria设置了密码,需要在设置中配置上密码即可 配置完密码重新加载就可以正常使用啦 下载速度明显比以前快了很多 下载参考文档 Docker安装下载神器aria2并使用过程记…...
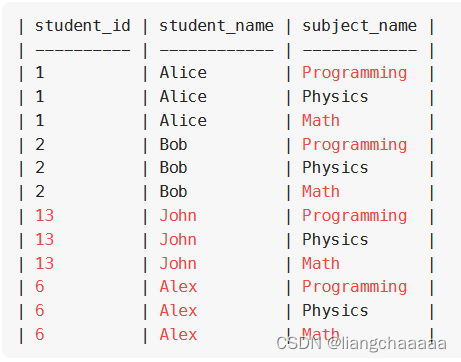
MYSQL 连接
高频 SQL 50 题(基础版) - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台 1378. 使用唯一标识码替换员工ID SELECT COALESCE(unique_id, NULL) AS unique_id,name FROM Employees LEFT JOIN EmployeeUNI ON Employees.…...

SeaTunnel 换maven源,解决插件下载慢
SeaTunnel 是使用的mvnw命令,可以先执行一下install-plugin.sh然后终止 理论上应该可以直接执行mvnw,他就会去安装下载maven,目录就是下面的目录 然后去服务器目录修改 setting.xml文件,设置镜像源即可 /root/.m2/wrapper/dists/apache-maven-3.8.4-bin/52ccbt68d252mdldqsfsn…...
安卓14通过“冻结”缓存应用程序腾出CPU,提高性能和内存效率
本月早些时候,我们听说更新到安卓14似乎提高了谷歌Pixel 7和Pixel 6的效率——提高了电池寿命,并在这个过程中减少了热量的产生。现在看来,安卓14的增效功能细节已经公布。 安卓侦探Mishaal Rahman在X(前身为Twitter)…...

jupyter崩溃OOM,out of memory,jupyter代码写不进去,保存不了。
最近写一个比较长的数据处理代码,有快千行,然后经常代码没有写入,然后直接网页崩溃,给我干蒙了。我已经是jupyter版本的问题,弄了半天,弄完,还是有这个问题。然后就查了一下,发现是j…...
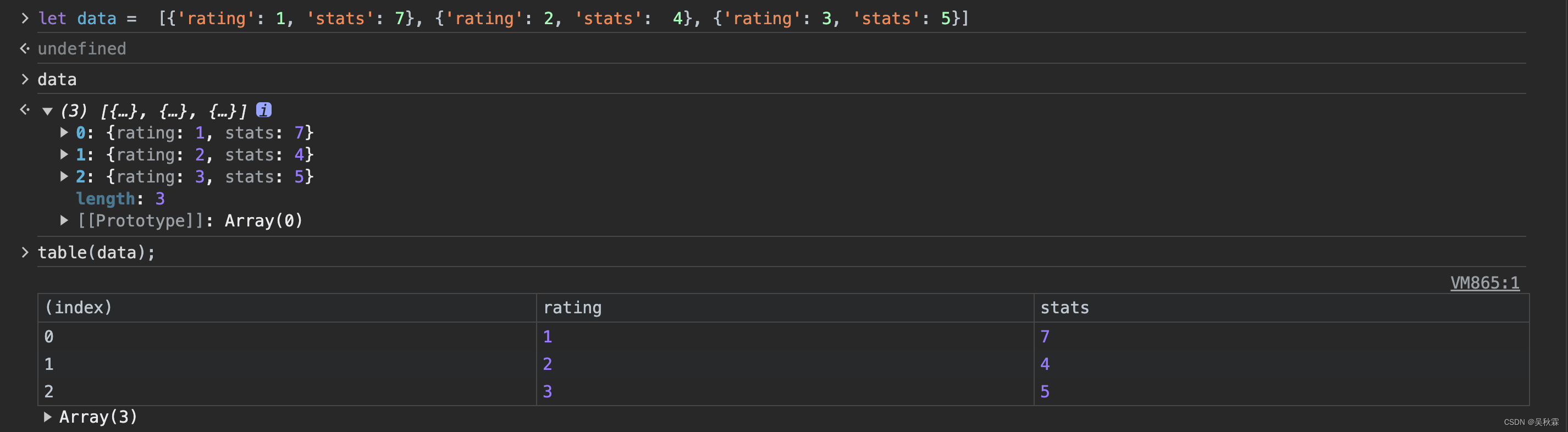
一文带你快速掌握爬虫开发中的一些高级调试技巧
文章目录 1. 写在前面2. Reply XHR(重新发起请求)3. copy as fecth(修改参数请求)4. copy()复制变量5. Web网页全屏截图6. 控制台安装使用npm7. 控制台中引用上次执行结果8. 控制台表展示对象数组 1. 写在前面 做过爬虫开发的人都…...

6.(vue3.x+vite)路由传参query与params区别
前端技术社区总目录(订阅之前请先查看该博客) 效果截图 一:路由传参有两种方式:params与query params与query区别 1:param,路由带“/”,query带“?” 2:query传过来的参数会显示到地址栏中 而params传过来的参数可以显示参数或隐藏参数到地址栏中(vue-router 4.1.4不…...

C++string的使用
CSDN的uu们,大家好。这里是C入门的第十六讲。 座右铭:前路坎坷,披荆斩棘,扶摇直上。 博客主页: 姬如祎 收录专栏:C专题 目录 1.构造函数 1.1 string() 1.2 string(const char* s) 1.3 string(const …...

闲着也是闲着,自己写歌东西玩一玩,碰碰脑子,简单快乐一点,双人出数的小游戏,后续还带补充
主旨就是每个人出一个数,目前限制两人,之后考虑多人,然后对其取差值,获取到一个结果,比对结果的奇偶数,还可以看下两人出同一个数的概率,反正概率上是一个比较稳定的。 当然自己想玩的活也可以做…...

牛客网 -- WY28 跳石板
题目链接: 跳石板_牛客题霸_牛客网 (nowcoder.com) 解题步骤: 参考代码: void get_approximate(vector<int>& v,int n) {//求约数,从2到sqrt(n)即可,原因看图解//这里一定要等于sqrt(n),例如16…...

[正式学习java③]——字符串在内存中的存储方式、为什么字符串不可变、字符串的拼接原理,键盘录入的小细节。
一、字符串 1.字符串在内存中的存储方式 🔥在java中,内存中有两个地方可以存储字符串,一个是字符串池,一个是堆内存,串池中的字符串不会重复,而堆中的字符串每次都会开辟一块新的空间,因为维护…...
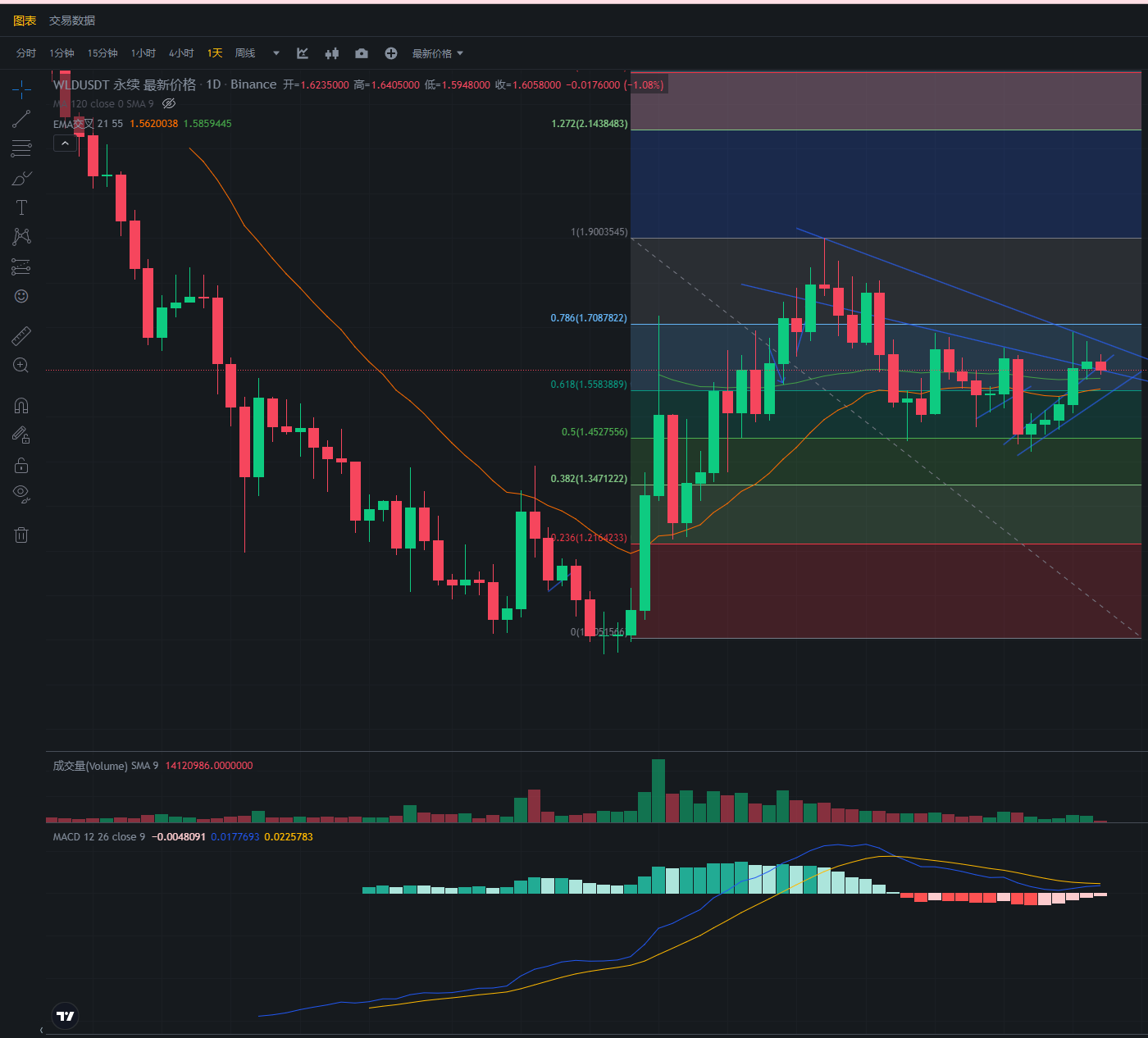
行情分析——加密货币市场大盘走势(10.18)
大饼昨日小幅度的下跌回调了,很快又上涨。目前看下来震荡向下刚刚开始,可以关注后续情况。大饼依然保持看空不做空,目前除了独立行情的币,就大饼非常强势。目前从MACD日线来看,还是保持多头趋势,预计明后两…...
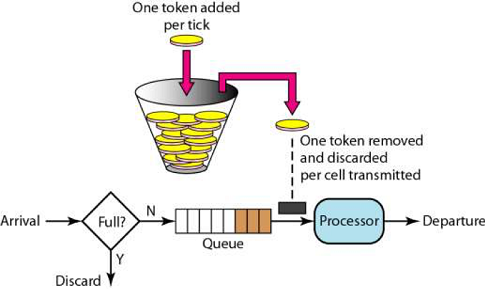
高并发场景下常见的限流算法及方案介绍
应用场景 现代互联网很多业务场景,比如秒杀、下单、查询商品详情,最大特点就是高并发,而往往我们的系统不能承受这么大的流量,继而产生了很多的应对措施:CDN、消息队列、多级缓存、异地多活。 但是无论如何优化&…...
虹科分享 | 选择SAS还是NVMe?虹科网络基础带您一探究竟!
存储架构师需要通过确保他们选择的存储解决方案提供支持其生态系统所需的安全性、稳定性、可扩展性和管理特性来应对当今的业务挑战。当他们考虑采用新的存储技术时,在采用新技术之前,他们应该权衡和审查一些基本的考虑因素。新的存储协议不断进入市场&a…...
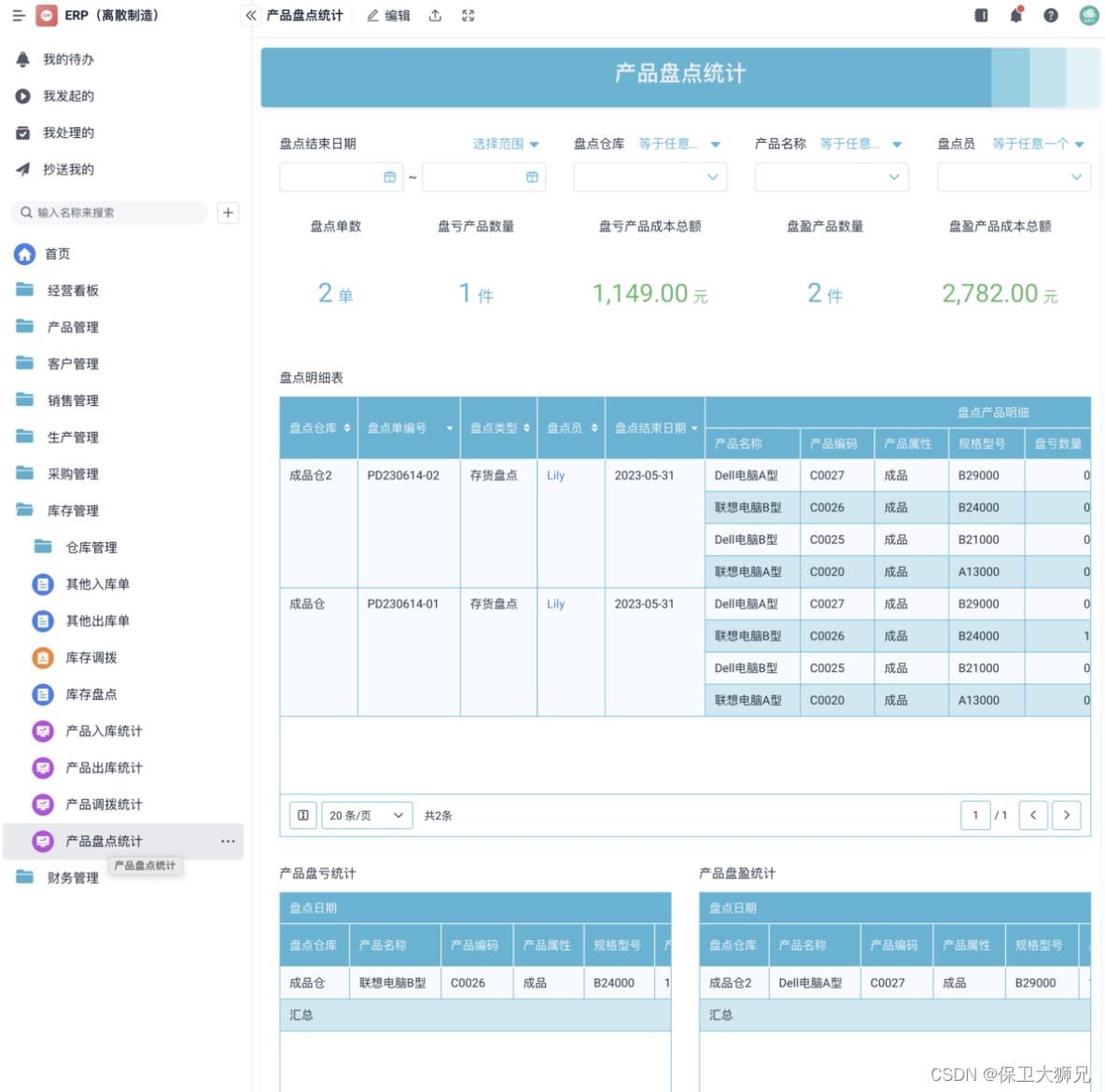
在ERP管理系统中,库存管理的基本流程是什么?
在ERP管理系统中,库存管理的基本流程是什么? 下面我就以我们公司正在用的简道云库存管理系统为例,为大家进行库存管理基本流程的演示 这个系统是我们公司自己搭建的,大家如果有需要可以自取,也可以在模板的基础上自行…...

Ruby 之 csv 文件读写
csv 文件写入 require csvtitle ["col1", "col2"] contents [["row11", "row12"], ["row21", "row22"]]csv1 CSV.open("test1.csv", "wb") do |csv|# write file titlecsv << titl…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...
