四边形不等式
区间dp问题,状态转移方程:
dp[i][j] = min( dp[i][k] + dp[k+1][j] +w[i][j] ) //w[i][j]是从i到j的,一个定值 不随k改变,而且w的值只和i j有关,是它们的二元函数。
其中i<=k<=j ,初始值dp[i][i]已知。
含义:
dp[i][j]是状态i到j的最小花费。
dp[i][k] + dp[k+1][j]体现递推关系,k在i和j之间滑动,k有一个最优值使dp最小。
w[i][j]的性质很重要!w[i][j]是和题目有关的费用,如果满足四边形不等式和单调性,那么用DP计算dp时,就可以用四边形不等式进行优化。
看w函数,
单调性:【如果大区间包含小区间,那么大区间的w值也大于】
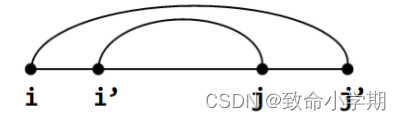
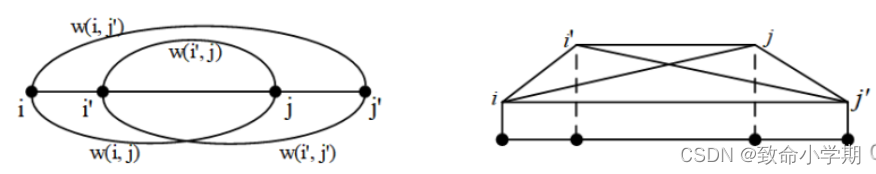
四边形不等式:
i,i',j,j' w[i,j]+w[i',j']<=w[i,j']+w[i',j] 交叉区间的和<=大区间和小区间的和
如果w满足单调性和四边形不等式的话,dp也满足。
dp[i][j]的最优分割点记为s[i][j],那么 s[i][j-1] <= s[i][j] <=s[i+1][j]
打表观察是否满足:
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
int w(int i,int j)
{//具体问题具体分析
}
int main()
{bool flag=true;//验证单调性 for(int l=1;l<=n;l++)for(int r=l+2;r<=n;r++)for(int i=l;i<=r;i++)for(int j=i;j<=r;j++)if(w(i,j)>w(l,r)) flag=false;//验证四边形不等式 for(int l=1;l<=n;l++)for(int r=l+2;r<=n;r++)if(w(l,r-1)+w(l+1,r)>w(l,r)+w(l+1,r-1)) flag=false;if(flag) //符合单调性以及四边形不等式else //不符合单调性以及四边形不等式return 0;
} 相关文章:
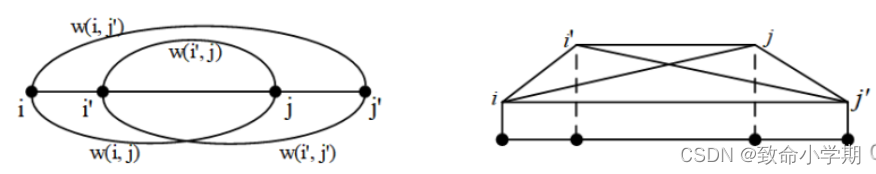
四边形不等式
区间dp问题,状态转移方程: dp[i][j] min( dp[i][k] dp[k1][j] w[i][j] ) //w[i][j]是从i到j的,一个定值 不随k改变,而且w的值只和i j有关,是它们的二元函数。 其中i<k<j ,初始值dp[i][i]已知。 含义&#x…...

Jmeter(四):请求默认值元件应用,正则表达式提取器元件讲解
Jmeter请求默认值元件应用 HTTP请求默认值 在公司内部进行测试的时候,一般测试环境访问的接口地址(服务器名称 或IP)、端口、协议一般都是不变的,但http请求取样器每个请求都要求写一遍 这些信息,在实际HTTP请求取样…...

LCR 001. 两数相除
剑指Offer通关 力扣搜索LCR即为剑指Offer的所有题目。 LCR 001. 两数相除 快速乘 解析: 题目规定只能用32位整数,所以取值范围在-2^31 ~ 2^31 - 1 之间。这里的特殊情况为什么不考虑被除数和除数为最大值?因为后面会将所有的数都转为负数…...

LeCun和Bengio“吵”起来了,人工智能是“潘多拉魔盒”吗?
作者 | 谢年年 上周末,深度学习领域最有影响力的三巨头之二Yann LeCun和Yoshua Bengio就AI的潜在风险和安全问题引发了一场激烈辩论,人工智能是“潘多拉魔盒”吗?这场辩论引来众多AI知名人士围观。 LeCun在Facebook上发起了这场辩论ÿ…...
电子期刊制作宝典,让你成为专业行家
电子期刊作为一种新兴的媒体形式,越来越受到人们的喜爱。它不仅方便快捷,而且可以随时随地阅读,不受时间和空间的限制。那么,如何制作一份高质量的电子期刊呢? 1.首先打开FLBOOK电子杂志平台 2.然后点击模板选择电子期…...

ESP32网络开发实例-Web显示传感器实时数据
Web显示传感器实时数据 文章目录 Web显示传感器实时数据1、软件准备2、硬件准备3、代码实现3.1 Web页面代码实现4.2 Web服务器代码实现本文将详细介绍如何使用ESP32在 Web 服务器上绘制传感器读数(温度、湿度和压力)。 ESP32 将托管一个网页,其中包含三个实时图表,每 30 秒…...

ARM Cortex-A9:裸机开发,点亮LED3
1.看原理图 外设板原理图 核心板原理图 2.在芯片手册中找到控制硬件的有效的特殊功能寄存器 选择0x1输出 GPX1DAT[0]->GPX1_0 0->1/0 3.编程 start.s Makefile复制到桌面 使用超级终端,连接串口 随便写一个 选择串口 配置串口 板子上电马上按enter…...

QT学习day2
一、思维导图 作业: 使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数将登录按钮使用qt5版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admi…...
214. Devu和鲜花
214. Devu和鲜花 - AcWing题库 如果每个盒子里的花的数量是无限的,用隔板法可以得出答案是 现在每个盒子中区的花数要满足n个条件 我们可以求答案的补集,用全部方案数减去补集方案数 每一个不符合条件的要求为,设为Bi 补集方案数为就成了…...

【C++初阶(三)引用与内联函数】
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...

RK3288 Android11 mini-pcie接口 4G模组EC200A适配(含自适应功能)
这里写目录标题 1、修改驱动内核配置①使能USBNET功能②使能 USB 串口 GSM、CDMA 驱动③使能 USB 的 CDC ACM模式④使能PPP功能 2、使用lsusb命令查看是否识别到usb接口的“EC200A”4G模组3、在drivers/usb/serial/option.c添加VID和PID信息①添加VID和PID定义②在option_ids 数…...

Windows安装Jenkins
JDK 11 以上 https://github.com/adoptium/temurin11-binaries/releases/download/jdk-11.0.20%2B8/OpenJDK11U-jdk_x64_windows_hotspot_11.0.20_8.msi https://www.jenkins.io/download/ 下载windows安装版本 授权用户administrator logon as services windows(server)安装…...

计算属性,侦听属性,方法区别及例子
计算属性、监听属性和方法都是Vue中的重要概念,但它们在功能和使用上有所不同: 计算属性:计算属性是基于依赖进行缓存的属性,可以根据其他数据动态计算得出。计算属性会根据依赖自动更新,但是只有在其所依赖的数据发生…...
Windows工业三防平板全功能NFC近距离感应一维/二维扫描
Windows系统工业三防平板电脑是一种在智慧工厂仓储物流、MES数采、车载设备、设备检测、自动化控制等领域广泛应用的先进设备。此外,它还在公共服务领域,如高速交通、物流运输、电力检测、公务执法、银行金融、船舶装备、户外勘测、建筑工程、汽车检测、…...

git远端协同开发、解决冲突、分支合并、gitlab使用、远程仓库回滚、为开源项目贡献代码、git工作流,git pull和git fetch,变基
协同开发 避免冲突 张三:改了 settings.py 第一行,提交了 李四:改了 settings.py 第二行,提交了 你也在改setting.py ,没有拉取代码,不知道他们提交了,动了第二行,但是跟李四代码不一样 你要…...
ims-go项目搭建
通过集成开发工具Goland创建项目 整合Gin框架,在终端中输入如下命令: go get -u github.com/gin-gonic/gin 整合Gorm,安装命令如下: go get -u gorm.io/gorm 安装sqlserver驱动,安装命令如下: go get -u…...

2022最新版-李宏毅机器学习深度学习课程-P26 Recurrent Neural Network
RNN 应用场景:填满信息 把每个单词表示成一个向量的方法:独热向量 还有其他方法,比如:Word hashing 单词哈希 输入:单词输出:该单词属于哪一类的概率分布 由于输入是文字序列,这就产生了一个问…...
【Qt控件之QButtonGroup】概述及使用
概述 QButtonGroup 类提供了一个容器来组织一组按钮部件。 QButtonGroup 提供了一个抽象容器,可以将按钮部件放置其中。它不提供此容器的可视表示(请参见 QGroupBox,用于容器部件),而是管理组中每个按钮的状态。 一个…...

【开源分享】基于Html开发的房贷计算器,模仿新浪财经
房贷计算器是一种房贷计算的在线计算Web应用,按用户选择的贷款类型、贷款金额、期限、利率可计算得出每月月供参考、支付利息、还款总额这些信息。本文模仿新浪财经开发的房贷计算器。 作品预览 https://fangdai.gitapp.cn 源码地址 https://github.com/geeeeeee…...

ftp文件上传缓慢问题
问题描述 某环境下,通过vsftp上传文件缓慢。 问题分析 这个问题是由于服务器DNS导致,如果在内网机器中,配置了公网的DNS或者其他不能链接的DNS,会导致上传缓慢。 解决方案 目前有两种解决方式,任选其一即可&#…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
