数据挖掘(6)聚类分析
一、什么是聚类分析
1.1概述
- 无指导的,数据集中类别未知
- 类的特征:
- 类不是事先给定的,而是根据数据的相似性、距离划分的
- 聚类的数目和结构都没有事先假定。
- 挖掘有价值的客户:
- 找到客户的黄金客户
- ATM的安装位置
1.2区别·

二、距离和相似系数
2.1概述
- 原则: 组内数据有较高相似度、不同组数据不相似
- 相似性的度量(统计学角度):
- Q型聚类:对样本聚类(行聚类)
- R型聚类:对变量聚类(列聚类)

2.2Q型聚类(样本聚类、行聚类)

1.样本资料矩阵:

2.定义距离的准则:
3.变量的类型
- 间隔尺度变量(数值型变量):可加可比
- 有序尺度变量(叙述型变量):不可加可比
- 名义尺度变量(名义型变量):不可加不可比
4.间隔尺度变量(数值型变量)
缺点:数据集中存在变量取值范围相差十分悬殊,会造成大数吃小数现象。
数值与指标量纲有关
度量值的标准化:
- 将初始测量值转换为无单位变量。
- 常用零均值规范化

特例:比例数值变量
5.有序尺度变量
- 只可以不可加:比如各种排名、等级
- 步骤

6.名义尺度变量(符号变量)
-
两种类型
- 二元变量:
- 只有两个取值变量:如男女、开关、01
- 名义变量:
- 二元变量推广:如颜色变量(R,G,B)
- 二元变量:
-
二元变量计算:
-
差异矩阵法:

-
恒定的相似度
- 对称的二元变量:取值01内容同等价值、相同权值
- 如:男女
- 简单匹配系数
- 取值不一样(01或10)的个数在所有变量的比重
- 对称的二元变量:取值01内容同等价值、相同权值
-
非恒定的相似度
- 非对称二元变量:取值01内容重要程度不同
- 如:病毒阴阳性
- Jaccard相关系数
- 取值不一样(01或10)的个数在所有变量(除去取值为00)的比重
- 非对称二元变量:取值01内容重要程度不同
- 相似度系数例子(小题计算):

- 名义变量计算(最常用):


-
7.混合数据类型
- 现实数据库中包含多类型的数据
- 如何计算?
- 将变量按类型分组,对每种类型的变量单独聚类分析,但实际中,往往不可行。
- 将所有的变量一起处理,只进行一次聚类分析。
- 相似度计算



2.3R型聚类(变量聚类、列聚类)
-
相似系数:
- 夹角余弦
- 相关系数
-
夹角余弦
- 值越大越好

-
变量间相似系数

-
相似系数

-
相似矩阵
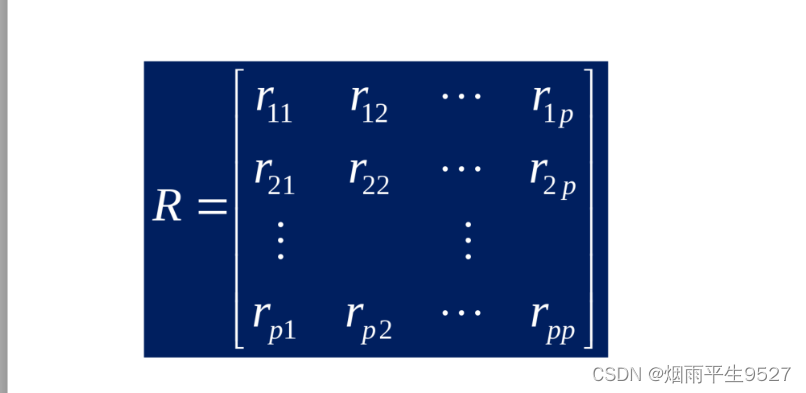
三、 类的定义和类间距离
3.1类的定义
- 定义1:任意元素
,间距离
满足:
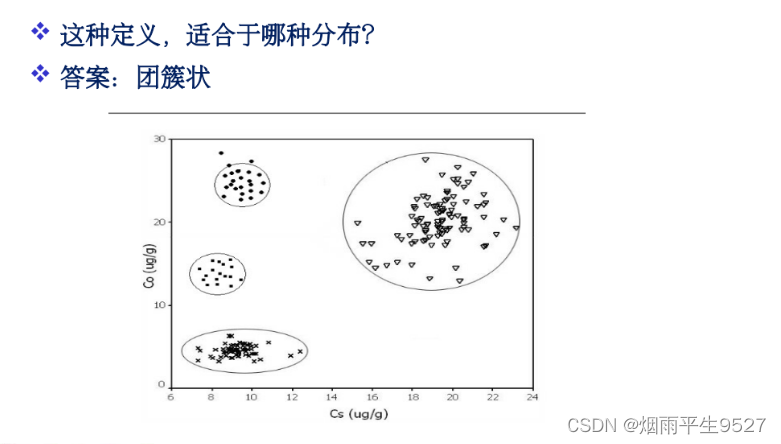
- 适合:团簇状
- 定义2:任意元素
,间距离
满足
(类内平均距离)
- 适合:团簇状
- 定义3:对于任意元素
,存在
使得其满足
(不要求任意两个元素)
- 适合:长条状
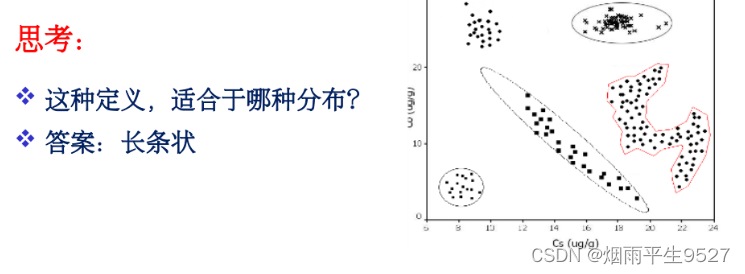
3.2类间距离
-
最近距离
-
与
最近距离为
-
是
和
,合并得到的
-
实际中不多见,避免极大值影响

-
例子
-
计算类间距离,然后将最小的两个进行合并

-
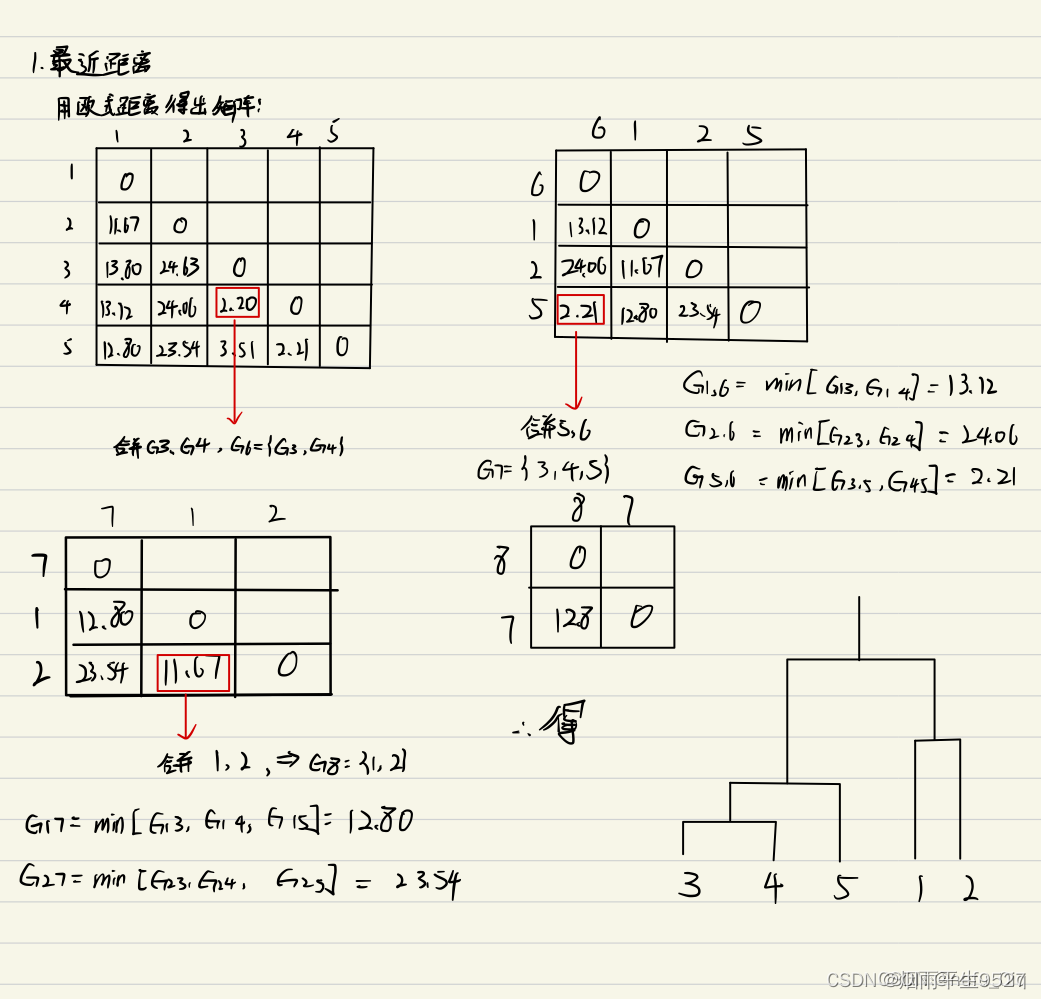
-
-
- 最远距离
与
最远距离为
是
和
,合并得到的
-
可能被极大值扭曲,删除后再聚类
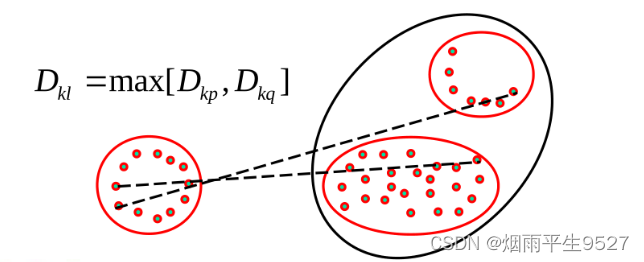
-
例题:与上面的类似,每次选取距离最小的,合并的时候取的是max
-
平均距离
-
- 中间距离
- 重心距离
-
一个类空间的位置用重心表示,两个类重心之间距离为二者的距离

-
对异常值不敏感,结果能稳定
-
四、基于划分的聚类方法
4.1划分方法
- 将n个对象划分成k类,且满足:
- 每个聚类内至少包含一个对象
- 每个对象必须属于一个类(模糊划分计划可以放宽要求)
- 划分方法:
- k-均值:每个聚类用该聚类中对象的平均值表示
- k-中心点:每个聚类用接近聚类重心的一个对象(真实存在的点)表示
4.2k-均值聚类算法
-
用类均值表示
-
不适合处理离散型属性,适合处理连续型属性
-
算法流程:

- 选取聚类中心:随机从n个数据选择k个对象作为初始聚类中心
- 对剩余的每个对象,根据各个聚类中心的距离,将其赋给最近的聚类。
- 重新计算每个聚类的平均值(中心)
- 不断重复,直到准则函数收敛(减小)
- 收敛准则函数:误差平方和最小

-
缺点:
-
局部最优,不是全局最优
-
结果与k的取值有关
-
不适合发现大小很不相同的簇、凹状的簇
*![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AwfktfUP-1641719199744)(/uploads/upload_98816f0f833feeb2da5536e0c31765d5.png =400x)]](https://img-blog.csdnimg.cn/1fec809c19684e9988326cf8ab99721c.png)
-
只有在簇的平均值被定义的情况下才能使用,不适合有类属性的数据。
-
对噪声、异常点敏感。
-
-
示意图例子:
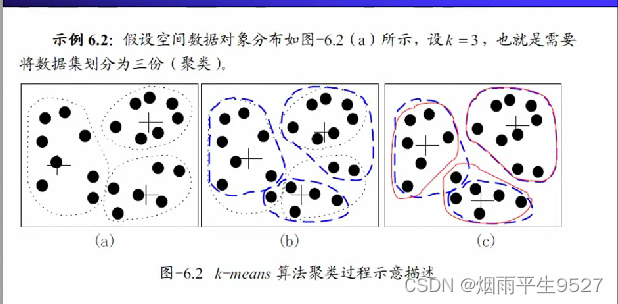
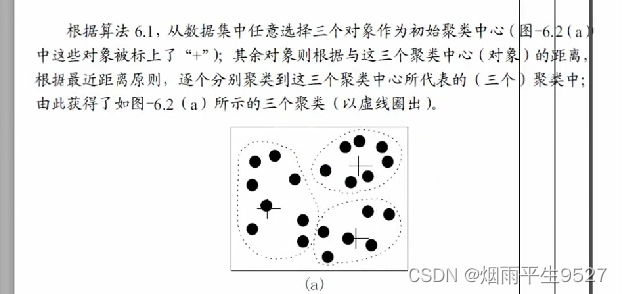
-

4.3k-中心点聚类算法
- k-中心点与k-均值算法区别
簇中心 评价准则 k-均值 簇中对象均值(可以是虚点) 误差平方和 k-中心点 接近簇中心的一个对象表示(实际存在的点) 绝对误差
- 基本策略
- 随意选择一个代表对象作为中心点,将剩余对象按最小距离划分进簇中。
- 重复利用非中心对象代替中心对象,若改善聚类的整体距离,则进行替代。
- 用代价函数进行估算质量:
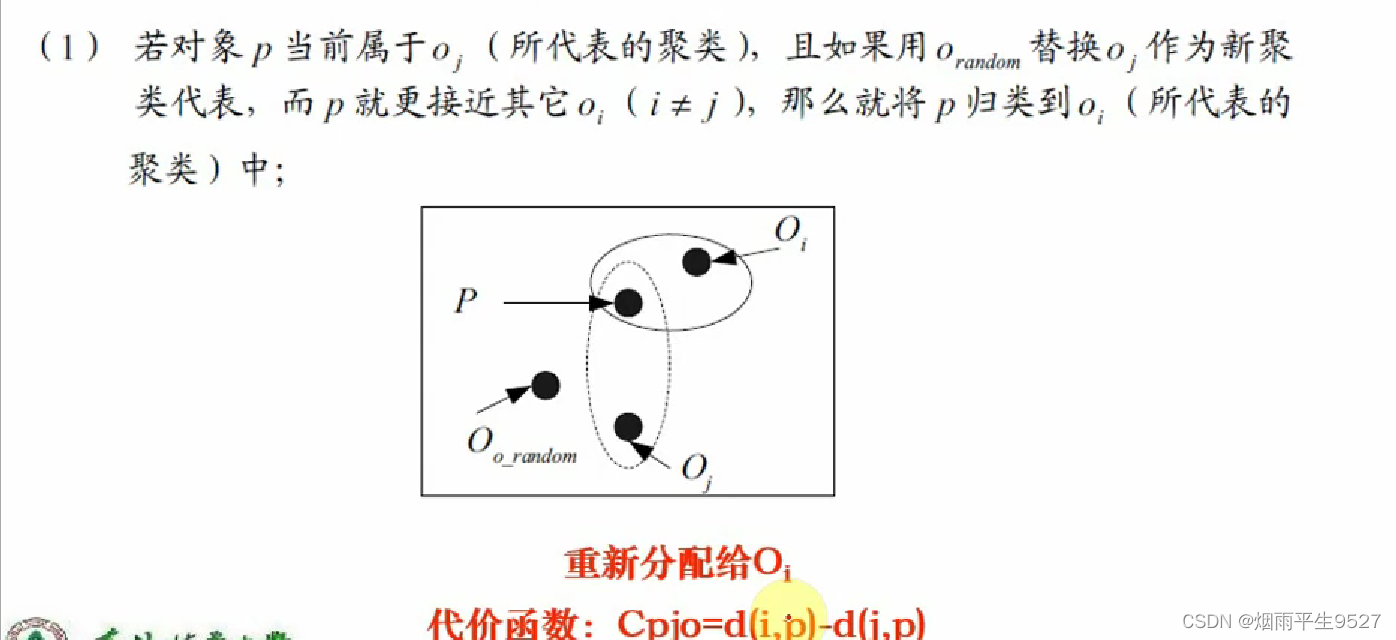
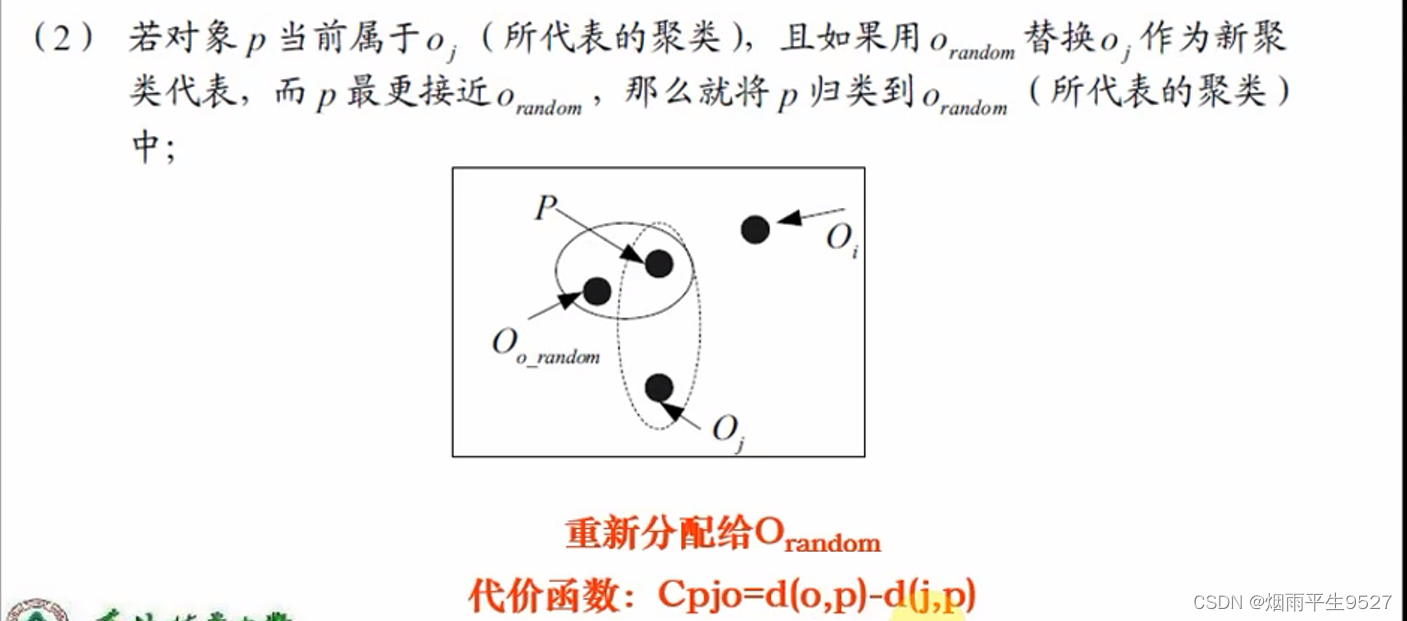
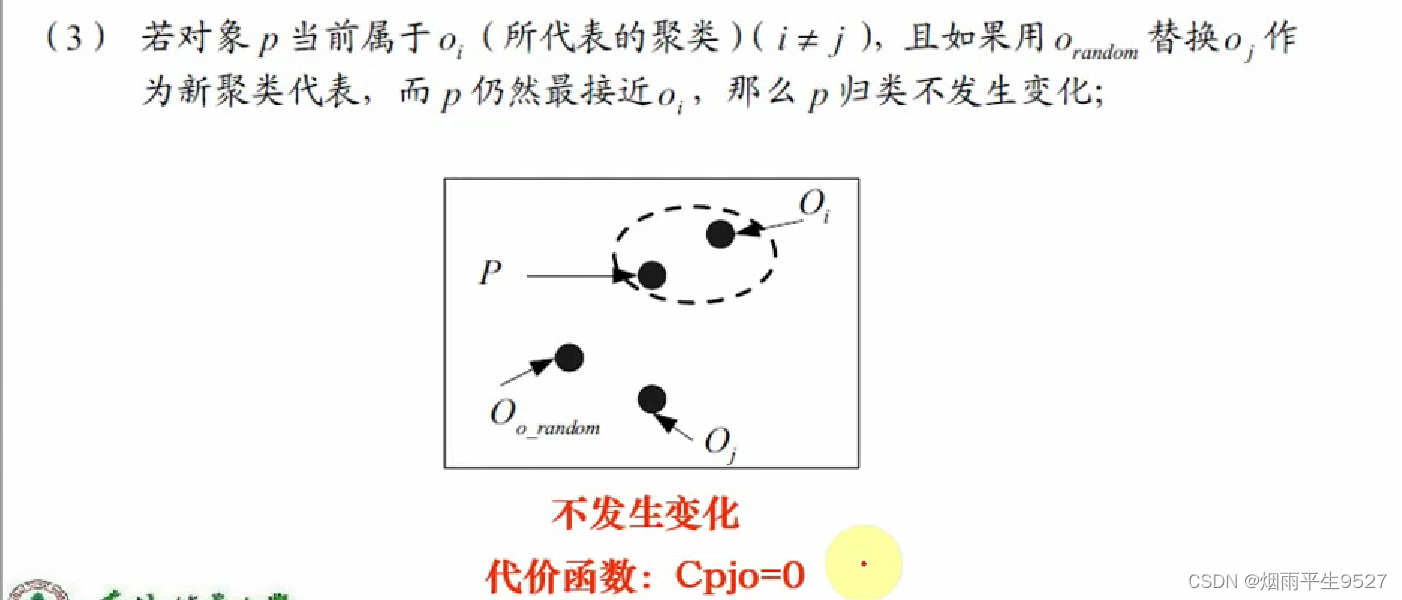
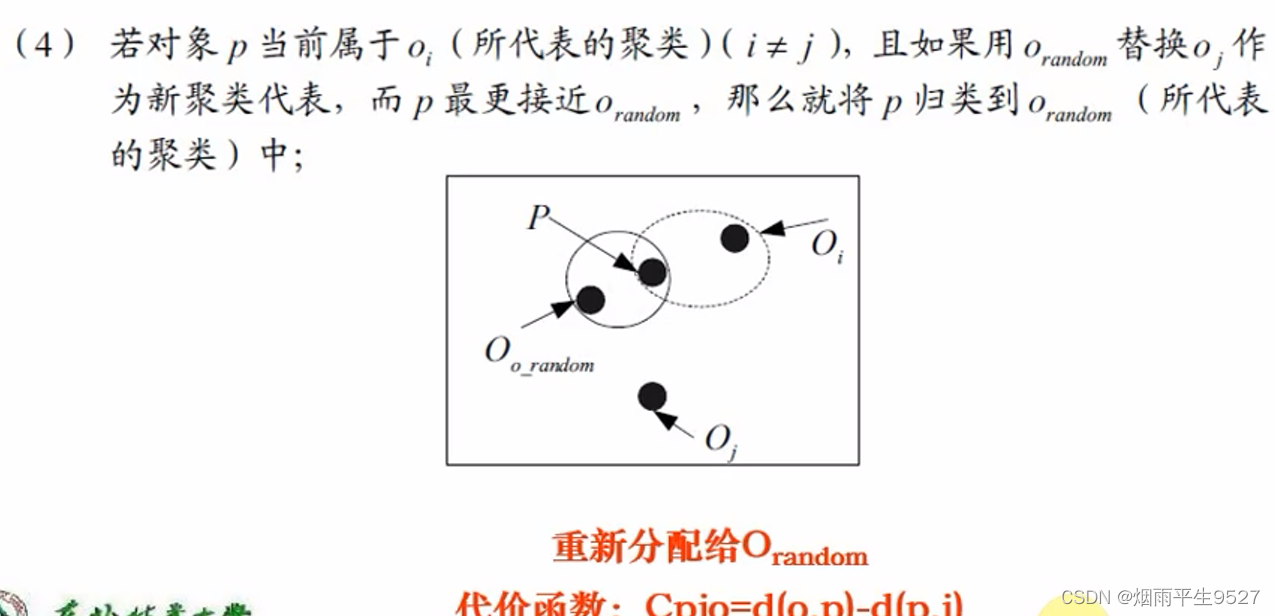
- 替代的四种情况
- 如何判断非代表对象
是否能替代当前代表对象
,需要对每个非中心点P考虑
- 替换的总代价:
- 若总代价为负,则可以替代
4.算法步骤
- 选取聚类中心:随机从n个数据对象选择k个
- 循环3-5,知道聚类不发生变化
- 对剩余的每个对象,根据各个聚类中心的距离,将其划分给最近的聚类。
- 选择任意非中心对象
计算与中心对象
交换的成本S。
- 若成本S为负,则交换中心对象。
五、基于层次的聚类方法
5.1 总述
- 给定的数据对象集合进行层次分解,根据层次分解的方式,层次的方法被分为凝聚、分裂。
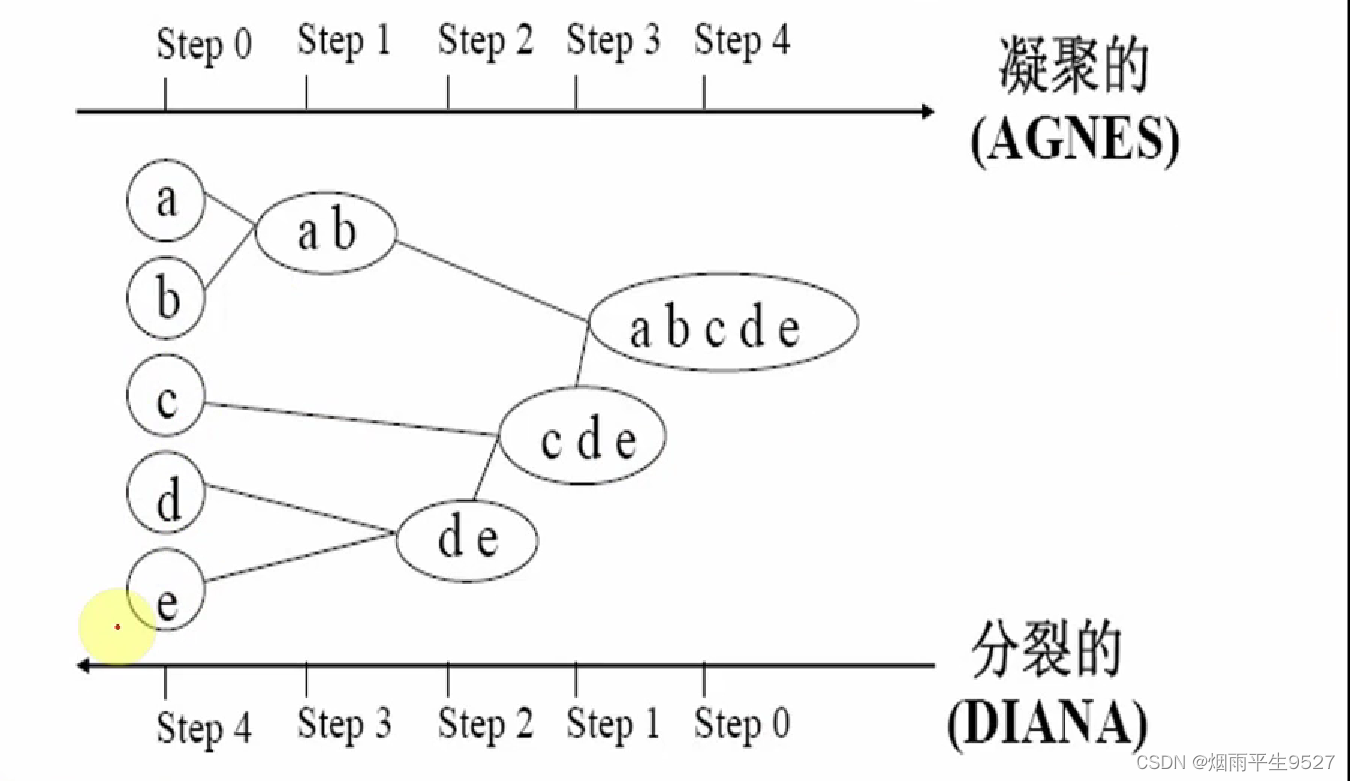
- 凝聚层次法(agnes算法)
- 自底向上
- 一开始将每个对象作为单独的一组,然后合并相近的组,直到合为一组或到达终止条件
- 分裂层次法(dinan算法)
- 自底向下
- 所有对象置于一个簇,在迭代的每一步,一个簇被分裂为更下的簇,直到每个对象单独为一个簇或到达某个终止条件
- 计算距离方法

5.2agnes算法
- 步骤:
- 每个对象当做一个初始簇
- repeant 3-4
- 根据两个簇中最近数据点找到最近的两个簇
- 合并两个簇,生成新的簇集合
- until 达到定义的簇的数目
- 例子

- 特点:
- 算法简单,合并会出现问题:一旦合并就不能撤销,可能会对后续操作产生影响。
- 复杂度比较大O(n^2)
5.3diana算法
- 簇的直径:一个簇中的任意两个数据点的距离中的最大值
- 平均相异度(平均距离):

- 算法步骤
将所有对象当做一个初始簇 for(int i = 1; i <= k; i++){在所以簇中挑选出最大直径的簇C找出C中与其他点平近距离最大的一个点p放入splinter group,剩余点放入old partyRepeat在old party中找出到splinter group比到old party更近的点,加入splinter groupUntil 没有新的点被分到splinter groupsplinter group 与 old party 就被分解为两个新的簇 } -
例题

六、 基于密度的聚类方法
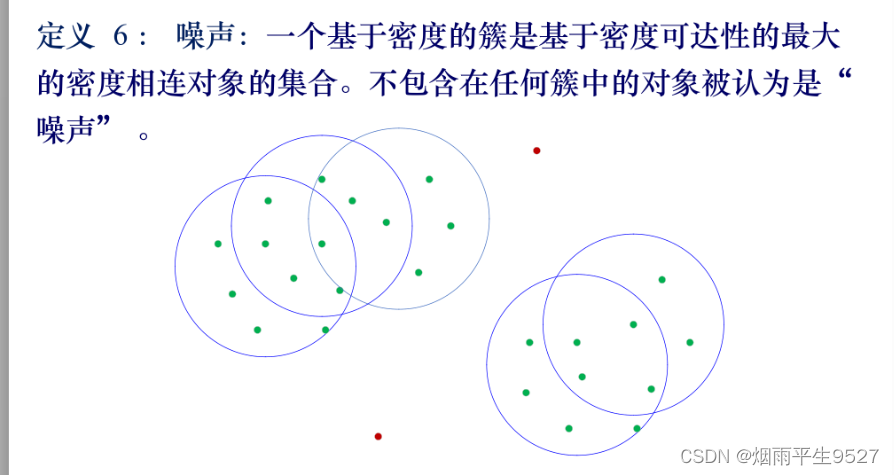
6.1概述
- 基于密度聚类方法
- 只要一个区域中点的密度(对象、数据点的数目)超过阈值,就将其加到与之相近的聚类中
- 可以过滤噪声、孤立点、发现任意形状的簇
- 代表算法:Dbscan、Optics、Denclue

相关文章:
数据挖掘(6)聚类分析
一、什么是聚类分析 1.1概述 无指导的,数据集中类别未知类的特征: 类不是事先给定的,而是根据数据的相似性、距离划分的聚类的数目和结构都没有事先假定。挖掘有价值的客户: 找到客户的黄金客户ATM的安装位置 1.2区别 二、距离和相似系数 …...
在启智平台上安装anconda
安装Anaconda3-5.0.1-Linux-x86_64.sh python版本是3.6 在下面的网站上找到要下载的anaconda版本,把对应的.sh文件下载下来 https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 把sh文件压缩成.zip文件,拖到启智平台的调试页面 上传到平台上 un…...

棒球省队建设实施办法·棒球1号位
棒球省队建设实施办法 1. 建设目标与原则 提升棒球省队整体竞技水平 为了提升棒球省队整体竞技水平,我们需要采取一系列有效的措施。 首先,我们应该加强对棒球运动的投入和关注。各级政府和相关部门应加大对棒球运动的经费投入,提高球队的…...

架构案例2017(五十二)
第5题 阅读以下关于Web系统架构设计的叙述,在答题纸上回答问题1至问题3.【说明】某电子商务企业因发展良好,客户量逐步增大,企业业务不断扩充,导致其原有的B2C商品交易平台己不能满足现有业务需求。因此,该企业委托某…...

给四个点坐标计算两条直线的交点
文章目录 1 chatgpt42、文心一言3、星火4、Bard总结 我使用Chatgpt4和文心一言、科大讯飞星火、google Bard 对该问题进行搜索,分别给出答案。先说结论,是chatgpt4和文心一言给对了答案, 另外两个部分正确。 问题是:python 给定四…...

从入门到进阶 之 ElasticSearch SpringData 继承篇
🌹 以上分享 从入门到进阶 之 ElasticSearch SpringData 继承篇,如有问题请指教写。🌹🌹 如你对技术也感兴趣,欢迎交流。🌹🌹🌹 如有需要,请👍点赞…...
中文编程开发语言工具编程案例:计时计费管理系统软件连接灯控器编程案例
中文编程开发语言工具编程案例:计时计费管理系统软件连接灯控器编程案例 中文编程开发语言工具编程案例:计时计费管理系统软件连接灯控器编程案例 中文编程系统化教程,不需英语基础。学习链接 https://edu.csdn.net/course/detail/39036...

YOLOv7改进:动态蛇形卷积(Dynamic Snake Convolution),增强细微特征对小目标友好,实现涨点 | ICCV2023
💡💡💡本文独家改进:动态蛇形卷积(Dynamic Snake Convolution),增强细长微弱的局部结构特征与复杂多变的全局形态特征,对小目标检测很适用 Dynamic Snake Convolution | 亲测在多个数据集能够实现大幅涨点 收录: YOLOv7高阶自研专栏介绍: http://t.csdnimg.…...

从文心大模型4.0与FuncGPT:用AI为开发者打开新视界
今天,在百度2023世界大会上,文心大模型4.0正式发布,而在大洋的彼岸,因为大模型代表ChatGPT之类的AI编码工具来势汹汹,作为全世界每个开发者最爱的代码辅助网站,Stack Overflow的CEO Prashanth Chandrasekar…...
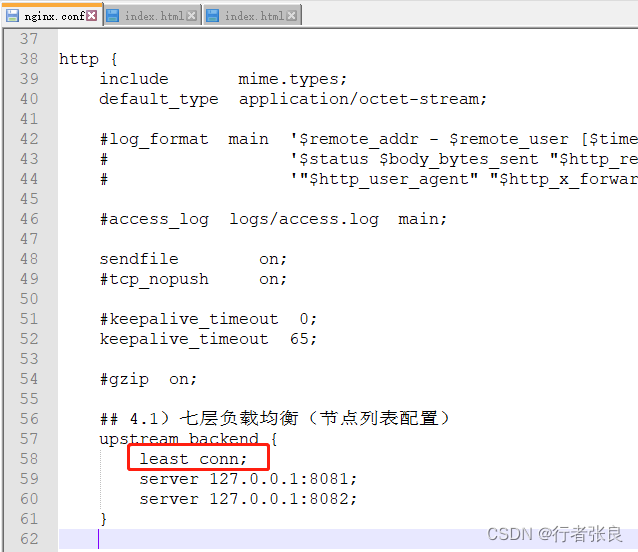
Nginx集群负载均衡配置完整流程
今天,良哥带你来做一个nginx集群的负载均衡配置的完整流程。 一、准备工作 本次搭建的操作系统环境是win11,linux可配置类同。 1)首先,下载nginx。 下载地址为:http://nginx.org/en/download.html 良哥下载的是&am…...

如何生成SSH服务器的ed25519公钥SHA256指纹
最近搭建ubuntu服务器,远程登录让确认指纹,研究一番搞懂了,记录一下。 1、putty 第一次登录服务器,出现提示: 让确认服务器指纹是否正确。 其中:箭头指向的 ed25519 :是一种非对称加密的签名方法…...
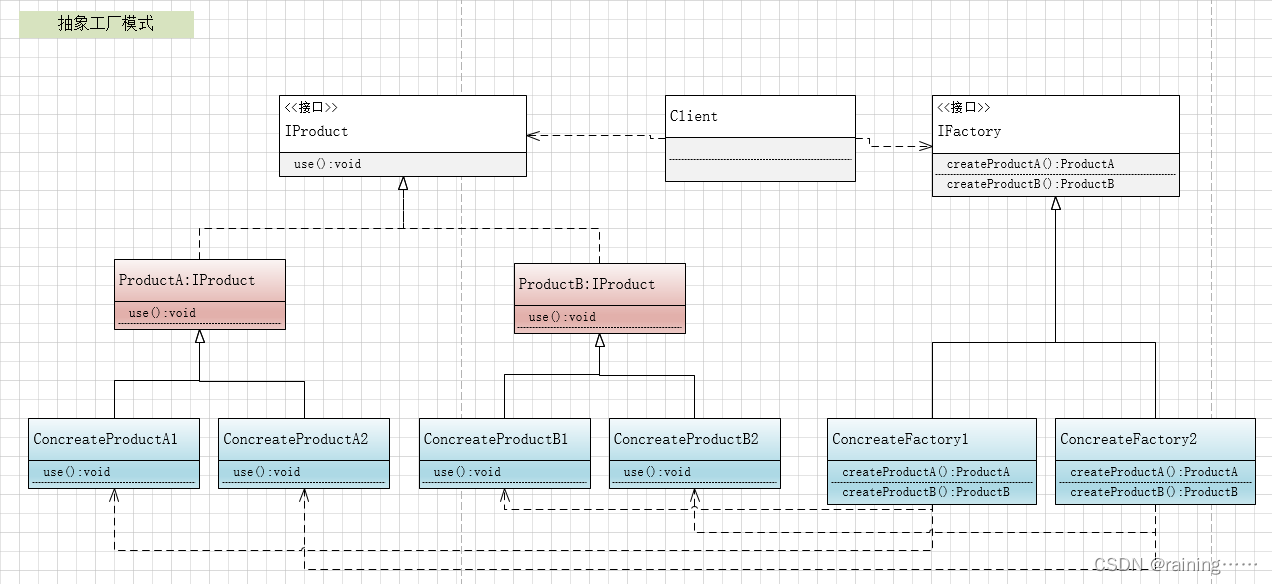
设计模式:抽象工厂模式(C#、JAVA、JavaScript、C++、Python、Go、PHP)
大家好!本节主要介绍设计模式中的抽象工厂模式。 简介: 抽象工厂模式,它是所有形态的工厂模式中最为抽象和最具一般性的一种形态。它用于处理当有多个抽象角色时的情况。抽象工厂模式可以向客户端提供一个接口,使客户端在不必指…...
、远程停止(RemoteStopTransaction))
ocpp-远程启动(RemoteStartTransaction)、远程停止(RemoteStopTransaction)
目录 1、介绍 2、远程启动-RemoteStartTransaction 3、远程停止-RemoteStopTransaction 4、代码 4.1 OcppRechongFeign 4.2 CmdController 4.3 CmdService 4.4 RemoteStartTransactionReq 4.5 接收报文-DataAnalysisController 4.6 接收报文实现类-DataAnalysisServi…...
【网络安全】安全的系统配置
系统配置是网络安全的重要组成部分。一个不安全的系统配置可能会使网络暴露在攻击者面前,而一个安全的系统配置可以有效地防止攻击者的入侵。在本文中,我们将详细介绍如何配置一个安全的系统,包括操作系统配置,网络服务配置&#…...

conda使用一般步骤
Terminal:conda create --name myenv python3.7 如果环境不行的话 1.source /opt/anaconda3/bin/activate 2.可能是没有源 vim ~/.condarc将需要的源装上 conda clean -i将原先的源删除 3.然后再conda create即可 4.需要激活环境 conda activate numpy 5.pycharm配置…...
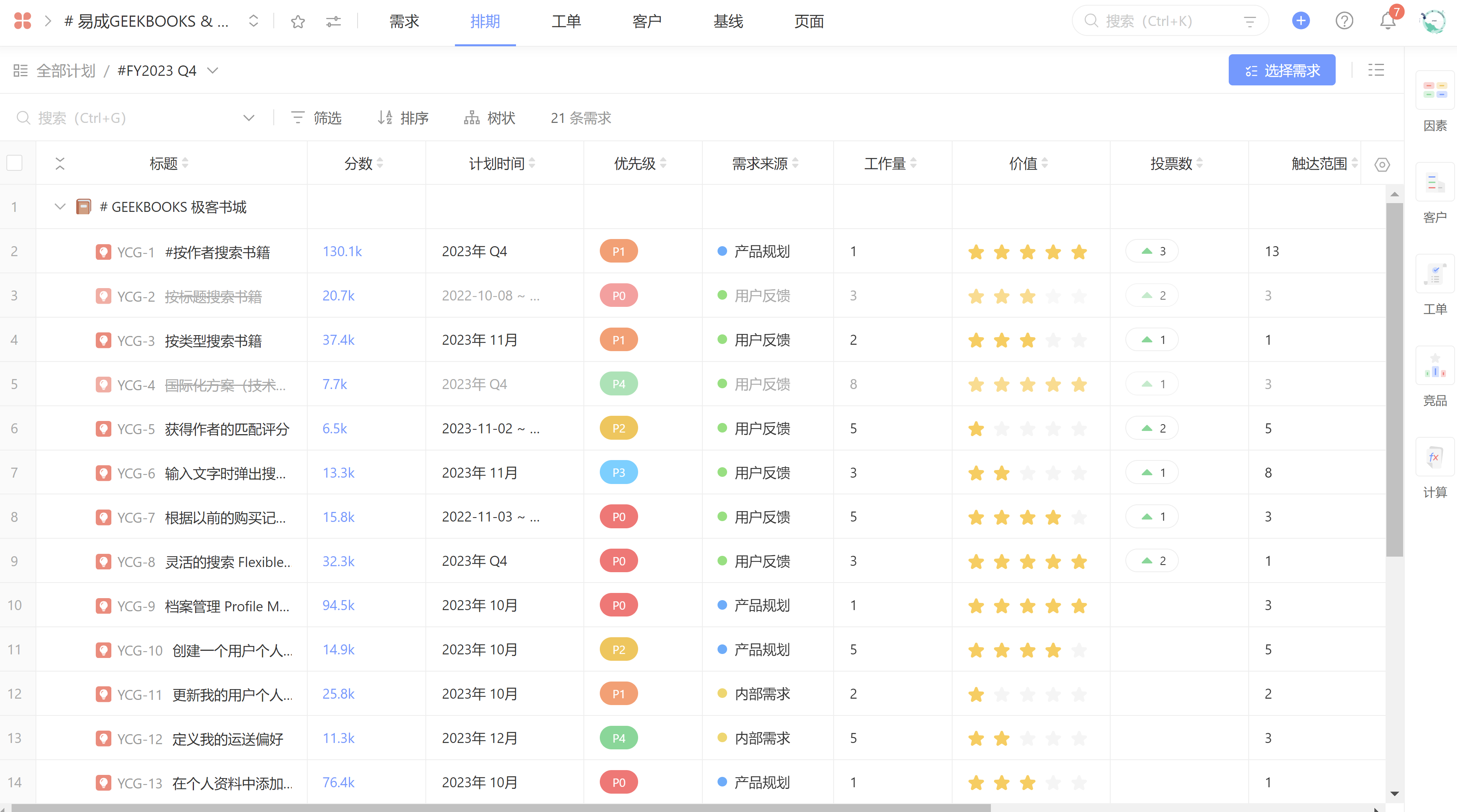
如何做好需求收集?方法和步骤
需求收集是理解你想要构建什么以及为什么要构建它的过程。需求收集通常被视为开发软件应用,或开发硬件产品的一部分。其重要性不言而喻。据调查显示50%以上产品在市场上失败的原因,是由于忽视了用户需求。 一、需求收集为什么会困难? 困扰项…...

SpringBoo整合WebSocket实战演练——Java入职十三天
前言 本文将介绍如何在Spring Boot应用程序中使用WebSocket实现服务端向客户端推送消息。Spring Boot和WebSocket的整合实现服务端向客户端推送消息,使得客户端能够实时接收并处理服务器发来的信息。WebSocket协议是一种双向通信的网络协议,使得客户端和服务器能够建立持久连…...

众佰诚:抖音小店的体验分什么时候更新
随着移动互联网的发展,越来越多的电商平台开始涌现,其中抖音小店作为一种新型的电商模式,受到了许多用户的欢迎。然而,对于抖音小店的体验分更新时间,很多用户并不是很清楚。本文将对此进行详细的解答。 首先ÿ…...

详解cv2.addWeighted函数【使用 OpenCV 添加(混合)两个图像-Python版本】
文章目录 简介函数原型代码示例参考资料 简介 有的时候我们需要将两张图片在alpha通道进行混合,比如深度学习数据集增强方式MixUp。OpenCV的addWeighted提供了相关操作,此篇博客将详细介绍这个函数,并给出代码示例。🚀Ƕ…...
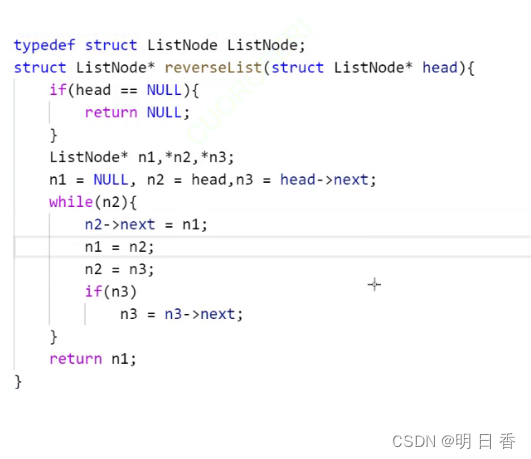
单链表经典OJ题:反转链表
题目: 给你单链表的头节点 head ,i请你反转链表,并返回反转后的链表。 图例: 分析: 根据链表的特征,反转链表的本质便是改变节点内部的指针方向。 将原先指向下一个节点的指针进行修改,将其的…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

STL 2迭代器
文章目录 1.迭代器2.输入迭代器3.输出迭代器1.插入迭代器 4.前向迭代器5.双向迭代器6.随机访问迭代器7.不同容器返回的迭代器类型1.输入 / 输出迭代器2.前向迭代器3.双向迭代器4.随机访问迭代器5.特殊迭代器适配器6.为什么 unordered_set 只提供前向迭代器? 1.迭代器…...