数论分块
本质就是利用取整分数值的块状分布。
UVA11526 H(n)
题意: 求 ∑ i = 1 n n i \sum_{i=1}^{n} \frac {n}{i} ∑i=1nin。
解析:
⌊ n i ⌋ \lfloor \frac{n}{i} \rfloor ⌊in⌋ 只有 O ( n ) O(\sqrt n) O(n) 种取值,考虑将相同值同时处理。时间复杂度 O ( T n ) O(T\sqrt n) O(Tn)。
对于 i i i,其块右端点 j j j 满足: j = ⌊ n ⌊ n i ⌋ ⌋ j = \lfloor \dfrac{n}{\lfloor \frac{n}{i} \rfloor} \rfloor j=⌊⌊in⌋n⌋。
证明:对所有 ⌊ n i ⌋ = k \lfloor \frac{n}{i} \rfloor=k ⌊in⌋=k 的 i i i:由 k ≤ n i k \le \frac{n}{i} k≤in,有 ⌊ n k ⌋ ≥ ⌊ n n i ⌋ = ⌊ i ⌋ = i \lfloor\frac{n}{k}\rfloor \ge \lfloor {\frac{n}{\frac n i}} \rfloor= \lfloor i \rfloor = i ⌊kn⌋≥⌊inn⌋=⌊i⌋=i。
故 ⌊ n k ⌋ \lfloor\frac{n}{k}\rfloor ⌊kn⌋ 即 ⌊ n ⌊ n i ⌋ ⌋ \lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor} \rfloor ⌊⌊in⌋n⌋ 即为该块所在右端点。
代码
[AHOI2005] 约数研究
考虑约数 i i i 在 1 ∼ n 1 \sim n 1∼n 中出现次数,即 i i i 的倍数个数,为 n i \frac{n}{i} in。答案即为 ∑ i = 1 n ⌊ n i ⌋ \sum_{i=1}^{n} \lfloor{\frac{n}{i}}\rfloor ∑i=1n⌊in⌋。
时间复杂度 O ( n ) O(\sqrt n) O(n)。
代码
约数和
同样考虑约数的贡献,即求 ∑ i = 1 n i × ⌊ n i ⌋ \sum_{i=1}^{n} i \times \lfloor\frac{n}{i}\rfloor ∑i=1ni×⌊in⌋。
考虑到原式子 < ∑ i = 1 n n < \sum_{i=1}^n n <∑i=1nn,long long 即可。
时间复杂度 O ( n ) O(\sqrt n) O(n)。
代码
[CQOI2007] 余数求和
∑ i = 1 n k m o d i = ∑ i = 1 n ( k − ⌊ k i ⌋ i ) = n k − ∑ i = 1 n ⌊ k i ⌋ i \sum_{i=1}^n k \bmod i \\ =\sum_{i=1}^n (k - \lfloor{\frac{k}{i}}\rfloor i) \\ =nk-\sum_{i=1}^n \lfloor{\frac{k}{i}}\rfloor i i=1∑nkmodi=i=1∑n(k−⌊ik⌋i)=nk−i=1∑n⌊ik⌋i
枚举到 k k k 即可, n , k n,k n,k 同阶时时间复杂度 O ( n ) O(\sqrt n) O(n)。
CF1485C Floor and Mod
妙。
法一:
⌊ a b ⌋ = a m o d b \lfloor \frac{a}{b} \rfloor = a\bmod b ⌊ba⌋=amodb
⌊ a b ⌋ = a − ⌊ a b ⌋ b \lfloor \frac{a}{b} \rfloor = a - \lfloor \frac{a}{b} \rfloor b ⌊ba⌋=a−⌊ba⌋b
⌊ a b ⌋ = a b + 1 \lfloor \frac{a}{b} \rfloor = \frac{a}{b+1} ⌊ba⌋=b+1a
有 b + 1 ∣ a b+1 \mid a b+1∣a。
由 ⌊ a b ⌋ < b \lfloor \frac{a}{b} \rfloor < b ⌊ba⌋<b,得 a < b 2 + b a < b^2+b a<b2+b。
而 b + 1 ∣ a b+1 \mid a b+1∣a,由 a < b 2 + b a < b^2+b a<b2+b,得 b ∤ a b \nmid a b∤a,故 ⌊ a b ⌋ = a b + 1 \lfloor \frac{a}{b} \rfloor = \frac{a}{b+1} ⌊ba⌋=b+1a。
综上, b + 1 ∣ a b+1 \mid a b+1∣a 且 a < b 2 + b a < b^2 + b a<b2+b 是原命题的一个充要条件。
答案即为
∑ b = 1 y min ( x , b 2 + b − 1 ) b + 1 \sum_{b=1}^{y} \dfrac{\min(x,b^2+b-1)}{b+1} b=1∑yb+1min(x,b2+b−1)。
分段整除分块即可。
总结:根据整除关系、范围得到一些性质,从而找出充要条件。
代码
法二(官方做法)
记 ⌊ a b ⌋ = a m o d b = k \lfloor \frac{a}{b} \rfloor = a\bmod b = k ⌊ba⌋=amodb=k。
a = k b + k a = kb + k a=kb+k
b + 1 = a k b+1=\frac{a}{k} b+1=ka
由 k < b k < b k<b,得 k + 1 < a k k+1<\frac a k k+1<ka,故 k k k 为根号级别。
枚举 k k k,考虑 b b b 的数量。可得 b ≤ x k − 1 b \le \frac x k - 1 b≤kx−1,且 k < b ≤ y k < b \le y k<b≤y。
总结:观察 + 放缩 k k k 的范围。
代码
相关文章:

数论分块
本质就是利用取整分数值的块状分布。 UVA11526 H(n) 题意: 求 ∑ i 1 n n i \sum_{i1}^{n} \frac {n}{i} ∑i1nin。 解析: ⌊ n i ⌋ \lfloor \frac{n}{i} \rfloor ⌊in⌋ 只有 O ( n ) O(\sqrt n) O(n ) 种取值,考虑将相同值同…...

宏任务与微任务,代码执行顺序
js引擎工作进程是同步的。事件循环机制,事件队列。 脚本代码执行顺序,是先执行同步代码,遇到微任务,就把它推进任务队列中。每个宏任务完成后,再执行下一个宏任务。 宏任务有哪些: i/o读写 定时器setTi…...

正方形(Squares, ACM/ICPC World Finals 1990, UVa201)rust解法
有n行n列(2≤n≤9)的小黑点,还有m条线段连接其中的一些黑点。统计这些线段连成了多少个正方形(每种边长分别统计)。 行从上到下编号为1~n,列从左到右编号为1~n。边用H i j和V i j表示…...

【算法设计与分析qwl】伪码——顺序检索,插入排序
伪代码: 例子: 改进的顺序检索 Search(L,x)输入:数组L[1...n],元素从小到大排序,数x输出:若x在L中,输出x位置下标 j ,否则输出0 j <- 1 while j<n and x>L[j] do j <- j1 if x<…...

Uniapp路由拦截-自定义路由白名单
步骤一:新建routerIntercept.js文件 步骤二:routerIntercept文件中写入:(根据自己需要修改whiteList白名单中的页面路径和自己的逻辑处理) import Vue from vue // 白名单 const whiteList = [/pages/public/login,/pages/public/privacyAgreement, ]export default asy…...
在中国可以使用 HubSpot 吗?
当谈到市场营销和客户关系管理工具时,HubSpot通常是一家企业的首选。然而,对于许多中国的企业来说,一个重要的问题是:在中国可以使用HubSpot吗?这个问题涉及到不同的方面,包括政策法规、社交媒体平台、语言…...

Java的基础应用
Java是一种广泛应用于软件开发的编程语言,基础应用涵盖了很多方面。以下是Java的一些基础应用方面的介绍: 1. 控制流语句:Java中的程序流程控制语句分为选择语句和循环语句。选择语句包括if-else语句和switch语句,循环语句包括fo…...
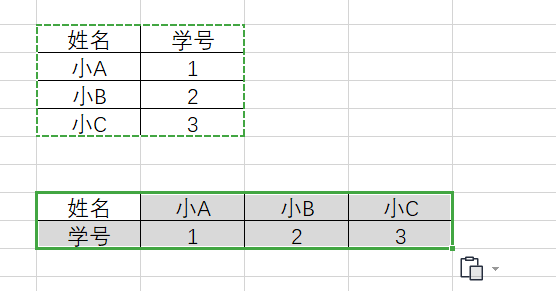
【excel】列转行
列转行 工作中有一些数据是列表,现在需要转行 选表格内容:在excel表格中选中表格数据区域。点击复制:在选中表格区域处右击点击复制。点击选择性粘贴:在表格中鼠标右击点击选择性粘贴。勾选转置:在选择性粘勾选转置选…...

用Bing绘制「V我50」漫画;GPT-5业内交流笔记;LLM大佬的跳槽建议;Stable Diffusion生态全盘点第一课 | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🔥 美国升级AI芯片出口禁令,13家中国GPU企业被列入实体清单 nytimes.com/2023/10/05/technology/chip-makers-china-lobbying…...

Java身份证实名认证-阿里云API 【姓名、身份证号】
1. 阿里云API市场 https://market.aliyun.com/products/57126001/cmapi00053442.html?spm5176.2020520132.101.3.a6217218nxxEiy#skuyuncode47442000022 购买对应套餐 2. 复制AppCode https://market.console.aliyun.com/imageconsole/index.htm#/?_kl85e10 云市场-已购买服…...

ND协议——无状态地址自动配置 (SLAAC)
参考学习:计算机网络 | 思科网络 | 无状态地址自动配置 (SLAAC) | 什么是SLAAC_瘦弱的皮卡丘的博客-CSDN博客 与 IPv4 类似,可以手动或动态配置 IPv6 全局单播地址。但是,动态分配 IPv6 全局单播地址有两种方法: 如图所示&#…...

iOS开发UITableView的使用,区别Plain模式和Grouped模式
简单赘述一下 的创建步骤 // 创建UITableView self.tableView [[UITableView alloc] initWithFrame:self.view.bounds style:UITableViewStylePlain]; // 设置数据源和代理 self.tableView.dataSource self; self.tableView.delegate self; // 注册自定义UITableViewCe…...

css美化滚动条
/*定义滚动条高宽及背景 高宽分别对应横竖滚动条的尺寸*/ ::-webkit-scrollbar { width: 8px; height: 8px; background-color: rgba(0,0,0,.2); } /*定义滚动条轨道 内阴影圆角*/ ::-webkit-scrollbar-track { -webkit-box…...
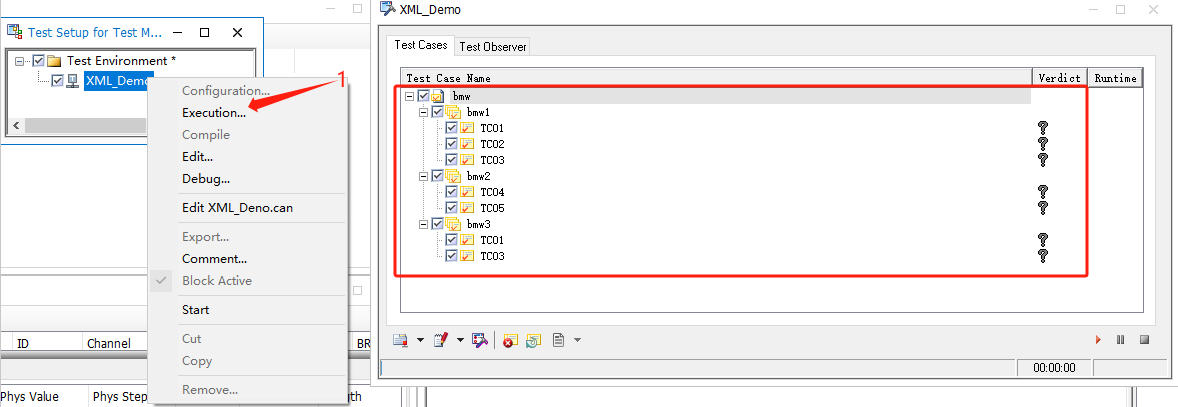
【CANoe】XML Test Module使用实例
文章目录 一、实操步骤1、增加XML Test Module节点2、配置XML Test Module节点3、XML Test Module节点增加CAPL脚本(.can文件)4、文件夹结构5、使用仿真节点开始测试6、测试结果与测试报告7、同理,在Test Setup也可如此操作 一、实操步骤 1、增加XML Test Module节…...

oracle的update语句where条件后的索引字段为空时不执行
问题描述: update 表名 set age ‘23’ where id1 and name‘lili’; 当在oracle执行以上sql时执行成功,但是当传入的name为null时,sql不成立。我的表中id和name是联合唯一索引,以为name不会为空,但实际上name可以为空…...

RabbitMQ的特点
RabbitMQ是一个开源的消息中间件,用于在不同的应用程序之间进行异步通信。它支持多种消息传递协议,如AMQP、MQTT、STOMP等。 RabbitMQ具有以下特点: 可扩展性:RabbitMQ可以通过添加更多的节点和队列来实现水平扩展。 可靠性&…...

JS单选框默认选中样式修改,为白色背景中心有黑色小圆点的样式
要修改JavaScript中默认选中的单选框的样式为白色背景并带有黑色小圆点,你可以使用CSS来实现。以下是一个示例,展示如何修改样式: <style>/* 修改默认选中单选框的样式 */input[type"radio"]:checked {appearance: none; /*…...

2023年下半年NPDP考试今天开始报名!
2023年第二次NPDP考试将于2023年12月2日(周六)举行,考试报名相关事项安排如下: 一、考试时间: 12月2日09:00-12:30。 二、报名时间: 10月18日08:00-11月10日23:59。 三、缴费及退考截止时间࿱…...
nfs+rpcbind实现服务器之间的文件共享
NFS简介 NFS服务及Network File System,用于在网络上共享存储,分为2,3,4三个版本,最新为4.1版本。NFS基于RPC协议,RPC为Remote Procedure Call的简写。 应用场景:用于A,B,C三台机器上需要保证被访问到的文件是一样…...

10-k8s-身份认证与鉴权
文章目录 一、ServiceAccount介绍二、ServiceAccount相关的资源对象三、dashboard空间示例 一、ServiceAccount介绍 ServiceAccount(服务账户)概念介绍 1)ServiceAccount是Kubernetes集群中的一种资源对象,用于为Pod或其他资源提供…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
