轻重链剖分+启发式合并专题
Codeforces-741D(Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths)
一棵根为1 的树,每条边上有一个字符(a-v共22种)。 一条简单路径被称为Dokhtar-kosh当且仅当路径上的字符经过重新排序后可以变成一个回文串。 求每个子树中最长的Dokhtar-kosh路径的长度。给你n个点构成的一棵树,树里面的每一条边有一个权值,求出每个子树里面能通过重排构成回文串的最大路径长度.
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,M=2*N;
int h[N],e[M],ne[M],w[M],idx;
int n,id[N],L[N],R[N],o,son[N],sz[N],dep[N],dfn[N];
int d[N],f[1<<23],ans[N],flag;
void add(int a,int b,int c){e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void dfs1(int u,int fa=0){dep[u]=dep[fa]+1;dfn[u]=++o,id[o]=u;sz[u]=1;L[u]=o;for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==fa)continue;d[j]=d[u]^w[i];//d[j]表示从根节点到j的结点状态dfs1(j,u);sz[u]+=sz[j];if(sz[son[u]]<sz[j])son[u]=j;}R[u]=o;
}
void upd(int u){if(f[d[u]])ans[u]=max(ans[u],f[d[u]]-dep[u]);for(int i=0;i<22;i++){int x=d[u]^(1<<i);if(f[x])ans[u]=max(ans[u],f[x]-dep[u]);}
}
void upd2(int j,int u){if(f[d[j]])ans[u]=max(ans[u],f[d[j]]+(dep[j]-dep[u])-dep[u]);for(int i=0;i<22;i++){int x=d[j]^(1<<i);if(f[x])ans[u]=max(ans[u],f[x]+(dep[j]-dep[u])-dep[u]);}
}
void cal(int u,int fa){upd(u);//先更新贡献f[d[u]]=max(f[d[u]],dep[u]);//把我自己插进去for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==son[u]||j==fa)continue;for(int x=L[j];x<=R[j];x++)upd2(id[x],u);//计算子树所有节点和我构成的贡献for(int x=L[j];x<=R[j];x++)f[d[id[x]]]=max(f[d[id[x]]],dep[id[x]]);//插入这颗子树的贡献}
}
void dfs(int u,int fa=0,int keep=0){for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==fa||j==son[u])continue;//先枚举轻儿子,不保留dfs(j,u,0);ans[u]=max(ans[u],ans[j]);}if(son[u]){//再计算重儿子,保留答案int j=son[u];dfs(j,u,1);ans[u]=max(ans[u],ans[j]);flag=j;}cal(u,fa);//计算跟u节点相关的答案flag=0;if(!keep)for(int i=L[u];i<=R[u];i++)f[d[id[i]]]=0;
}
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;memset(h,-1,sizeof h);char c;for(int i=2,j;i<=n;i++)cin>>j>>c,add(j,i,1<<(c-'a')),add(i,j,1<<(c-'a'));dfs1(1);dfs(1);for(int i=1;i<=n;i++)cout<<ans[i]<<" ";
}
阔力梯的树

用启发式合并写
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
int n,sz[N];
long long f[N];
vector<int>g[N],son[N];
set<int>S[N];
void dfs(int u){sz[u]=1;S[u].insert(u);for(auto j:g[u]){dfs(j);if(sz[u]<sz[j])swap(sz[u],sz[j]),swap(S[u],S[j]),f[u]=f[j];//这里swap有一个坑点,f[j]是你最后要用的,已经记录好了的不要乱动,u用了j的set直接从f[j]就好了for(auto x:S[j]){auto it=S[u].lower_bound(x);if(it==S[u].begin())f[u]+=(x-*it)*(x-*it);else if(it==S[u].end())it--,f[u]+=(x-*it)*(x-*it);else{int r=*it;it--;int l=*it;f[u]-=(r-l)*(r-l);f[u]+=(x-l)*(x-l)+(x-r)*(x-r);}S[u].insert(x);}sz[u]+=sz[j];}
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=2;i<=n;i++){int fa;cin>>fa;g[fa].push_back(i);}dfs(1);for(int i=1;i<=n;i++)cout<<f[i]<<'\n';
}
用树链剖分写
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
int n,h[N],ne[N],e[N],idx;
int sz[N],id[N],L[N],R[N],o,son[N],ans[N];
set<int>S;
int f;
void add(int a,int b){e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dsu(int u){sz[u]=1;L[u]=++o,id[o]=u;for(int i=h[u];~i;i=ne[i]){int j=e[i];dsu(j);if(sz[j]>sz[son[u]])son[u]=j;sz[u]+=sz[j];}R[u]=o;
}
void ins(int x){if(S.empty()){S.insert(x);return;}auto it=S.lower_bound(x);if(it==S.begin())f+=(x-*it)*(x-*it);else if(it==S.end())it--,f+=(x-*it)*(x-*it);else{int r=*it;it--;int l=*it;f-=(r-l)*(r-l);f+=(r-x)*(r-x)+(x-l)*(x-l);}S.insert(x);
}
void dfs(int u,int keep=0){for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==son[u])continue;dfs(j,0);}if(son[u])dfs(son[u],1);for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==son[u])continue;for(int k=L[j];k<=R[j];k++)ins(id[k]);}ins(u);ans[u]=f;if(!keep)f=0,S.clear();
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;memset(h,-1,sizeof h);for(int i=2;i<=n;i++){int fa;cin>>fa;add(fa,i);}dsu(1);dfs(1);for(int i=1;i<=n;i++)cout<<ans[i]<<'\n';
}
F. Strange Memory

#include<bits/stdc++.h>
// #define int long long
using namespace std;
const int N=2e5+10,M=1e6+5e5;
int n,h[N],e[N],ne[N],idx,a[N];
int L[N],R[N],id[N],o,sz[N],son[N];
int f[2][20][M];
long long ans;
void add(int a,int b){e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dsu(int u,int fa=0){sz[u]=1;L[u]=++o;id[o]=u;for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==fa)continue;dsu(j,u);if(sz[j]>sz[son[u]])son[u]=j;sz[u]+=sz[j];}R[u]=o;
}
void ins(int u,int k=1){for(int i=0;i<20;i++){int x=u>>i&1;f[x][i][a[u]]+=k;}
}
void cal(int u,int need){for(int i=0;i<20;i++){int x=u>>i&1;ans+=(1ll<<i)*(f[x^1][i][a[u]^need]);}
}
void dfs(int u,int fa=0,int keep=0){for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==fa||j==son[u])continue;dfs(j,u,0);}if(son[u])dfs(son[u],u,1);ins(u);//先去递归,再插入我自己,不然会wafor(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==fa||j==son[u])continue;for(int x=L[j];x<=R[j];x++)cal(id[x],a[u]);for(int x=L[j];x<=R[j];x++)ins(id[x]);}if(!keep)for(int i=L[u];i<=R[u];i++)ins(id[i],-1);
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);memset(h,-1,sizeof h);cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<n;i++){int a,b;cin>>a>>b;add(a,b);add(b,a);}dsu(1);dfs(1);cout<<ans;
}
E. Blood Cousins Return
树上gcd(x,y)==x^y的个数,操作1,插入新节点a[x]=v,操作2,合并x和y子树,操作3,把a[x]->v
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=3e5+10;
int n,m,p[N],sz[N],a[N];
ll ans;
vector<int>g[N];//g[i]表示i可能的答案,枚举i的约数存入进去
unordered_map<int,int>mp[N];
int find(int x){if(p[x]==x)return x;return p[x]=find(p[x]);
}
// a^b==gcd(a,b)有多少对
//a^b>=|a-b|>=gcd(a,b)void merge(int x,int y){x=find(x),y=find(y);if(x==y)return;if(sz[x]<sz[y])swap(mp[x],mp[y]),swap(sz[x],sz[y]);for(auto [k,v]:mp[y]){for(auto t:g[k])if(mp[x].count(t))ans+=(ll)mp[x][t]*v;}for(auto [k,v]:mp[y])mp[x][k]+=v;mp[y].clear();p[y]=x;sz[x]+=sz[y];
}
void so(int x){for(int d=1;d*d<=x;d++){if(x%d)continue;int i=d,j=x/i,y;y=x-i;if((x^y)==__gcd(x,y)&&y>0)g[x].push_back(y);y=x+i;if((x^y)==__gcd(x,y)&&y<=2e5)g[x].push_back(y);if(i==j)continue;y=x-j;if((x^y)==__gcd(x,y)&&y>0)g[x].push_back(y);y=x+j;if((x^y)==__gcd(x,y)&&y<=2e5)g[x].push_back(y);}
}
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);// for(int i=1;i<=2e5;i++)so(i);for (int i = 1; i <= 200000; i++) {for (int j = i + i; j <= 200000; j += i) {if (gcd(j, i^j) == i)g[j].push_back(i^j);}}cin>>n>>m;for(int i=1;i<=n+m;i++)p[i]=i,sz[i]=1;for(int i=1;i<=n;i++)cin>>a[i],mp[i][a[i]]++;while(m--){int op,x;cin>>op;if(op==1){int v;cin>>x>>v;a[x]=v;mp[x][v]=1;}if(op==2){int y;cin>>x>>y;merge(x,y);}if(op==3){int v;cin>>x>>v;int u=find(x);for(auto t:g[a[x]])if(mp[u].count(t))ans-=mp[u][t];mp[u][a[x]]--;a[x]=v;for(auto t:g[a[x]])if(mp[u].count(t))ans+=mp[u][t];mp[u][a[x]]++;}cout<<ans<<'\n';}
}
#include<bits/stdc++.h>
// #define int long long
using namespace std;
const int N=3e5+10;
int n,m,a[N],p[N];
long long ans;
vector<int>g[N];
int find(int x){if(p[x]==x)return x;return p[x]=find(p[x]);
}
void init(){for(int i=1;i<=2e5;i++){for(int j=i+i;j<=2e5;j+=i){if(__gcd(j,i^j)==i)g[j].push_back(i^j);}}
}
unordered_map<int,int>mp[N];
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);init();cin>>n>>m;for(int i=1;i<N;i++)p[i]=i;for(int i=1;i<=n;i++)cin>>a[i],mp[i][a[i]]=1;while(m--){int op,x,v;cin>>op>>x>>v;if(op==1)a[x]=v,p[x]=x,mp[x][v]=1;if(op==2){x=find(x),v=find(v);if(x!=v){if(mp[x].size()<mp[v].size())swap(mp[x],mp[v]);for(auto [a,c]:mp[v]){for(auto need:g[a])if(mp[x].count(need))ans+=(long long)c*mp[x][need];}for(auto [a,c]:mp[v])mp[x][a]+=c;// mp[v].clear();p[v]=x;}}if(op==3){int fa=find(x);int c=1;for(auto need:g[a[x]])if(mp[fa].count(need))ans-=c*mp[fa][need];mp[fa][a[x]]--;a[x]=v;for(auto need:g[a[x]])if(mp[fa].count(need))ans+=c*mp[fa][need];mp[fa][a[x]]++;}cout<<ans<<'\n';}}相关文章:

轻重链剖分+启发式合并专题
Codeforces-741D(Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths) 一棵根为1 的树,每条边上有一个字符(a-v共22种)。 一条简单路径被称为Dokhtar-kosh当且仅当路径上的字符经过重新排序后可以变成一个回文串。 求每个子树中…...
、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略)
IRC/ML:金融智能风控—信贷风控场景简介、两大场景(贷款场景+信用卡场景)、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略
IRC/ML:金融智能风控—信贷风控场景简介、两大场景(贷款场景+信用卡场景)、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略 目录 信贷风控简介 信贷风控两大场景...
【学习笔记】RabbitMQ01:基础概念认识以及快速部署
参考资料 RabbitMQ官方网站RabbitMQ官方文档噼咔噼咔-动力节点教程 文章目录 一、认识RabbitMQ1.1 消息中间件(MQ Message Queue 消息队列1.2 主流的消息中间件1.3 MQ的应用场景1.3.1 异步处理1.3.2 系统解耦1.3.3 流量削峰1.3.4 日志处理 二、RabbitMQ运行环境搭建…...

Java数据结构之第二十章、手撕平衡AVL树
目录 一、二叉平衡树 1.1二叉搜索树回顾以及性能分析 1.1.1二叉搜索树的概念 1.2二叉搜索树的查找 1.3二叉树查询性能分析 二、AVL树 2.1AVL树的概念 2.2AVL树节点的定义 2.3AVL树的插入 2.4AVL树的旋转 2.4.1新节点插入较高左子树的左侧---右单旋 2.4.2新节点插入较…...

SQL 在PostgreSQL中使用SQL将多行连接成数组
在本文中,我们将介绍如何使用SQL语言在PostgreSQL数据库中将多行数据连接成一个数组。在开发和分析应用程序时,我们经常需要将数据库中的多个行合并为一个,以便更方便地进行处理和分析。PostgreSQL提供了一种名为ARRAY_AGG的聚合函数…...

Ajax技术实现前端开发
一、原生AJAX 1.1AJAX 简介 AJAX 全称为Asynchronous JavaScript And XML,就是异步的JS 和XML。 通过AJAX 可以在浏览器中向服务器发送异步请求,最大的优势:无刷新获取数据。 AJAX 不是新的编程语言,而是一种将现有的标准组合在一起使用的新方式。 1.2XML 简介 XML 可扩…...

WebMail:网页注册成功发送邮件
1.特别注意 isELIgnored"false" 如果没有这个El表达式无法识别 2.pre work pox.xml <dependencies><dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>3.8.1</version><scope>…...
Electron之集成vue+vite开发桌面程序
在electron中集成vue开发桌面程序 使用我们之前创建的electron项目 创建vue 项目 命令行进入electron根目录 执行下面命令 npm create vitelatest vue -- --template vue这样就创建了一个vue项目,文件名是vue,命令行进入vue下,执行下面命…...

pycharm社区版创建Django项目的一种方式
pycharm社区版创建Django项目 pycharm创建New project安装django,如果安装过可略过安装完成后查看安装情况生成Django项目需要的文件这里注意生成语句后面的 . 不可以省略 生成文件后,框架搭建完成,配置启动我这里在配置完后,报了…...
Python configparser模块使用教程
文章目录 .ini 拓展名文件简介.ini 文件格式1. 节2. 参数3. 注解 configparser 模块简介configparser 模块的初始化和读取获取 ini 中所有 section获取 section 下的 key获取 section 下的 value获取指点section的所用配置信息修改某个key,如果不存在则会出创建检查…...

Kotlin + 协程 + Room 结合使用
文章目录 前言集成Room结合协程的使用总结 一、前言, 现在kotlin 是趋势,那必然就要用到协程,还有就是随着jetpack 的发力,带来了很多好用的库,比如今天提到Room,是一个类似greenDao的数据库。它不但支持kotlin协程…...
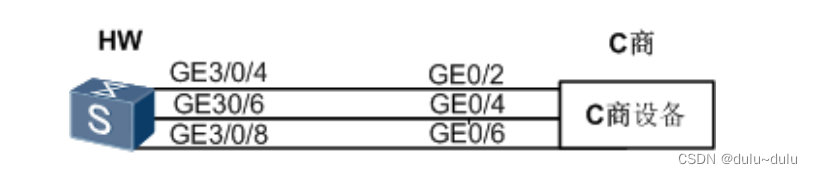
网工记背命令(6)----链路聚合配置
目录 1.配置手工负载分担模式链路聚合 2.配置LACP模式的链路聚合 3.HUAWEI设备与C厂商设备对接 链路聚合(Link Aggregation)是将多条物理链路捆绑在一起成为一条逻辑链路,从而增加链路带 宽的技术。 常用配置命令 1、执行命令 interface …...

使用 Service 把前端连接到后端
使用 Service 把前端连接到后端 如何创建前端(Frontend)微服务和后端(Backend)微服务。后端微服务是一个 hello 欢迎程序。 前端通过 nginx 和一个 Kubernetes 服务暴露后端所提供的服务。 使用部署对象(Deployment ob…...

vue 如何优化首页的加载速度?vue 首页白屏是什么问题引起的?如何解决呢?
vue 如何优化首页的加载速度? 路由懒加载ui框架按需加载gzip压缩 vue首页白屏是什么问题引起的 第一种,打包后文件引用路径不对,导致找不到文件报错白屏 解决办法:修改一下config下面的index.js中bulid模块导出的路径。因为in…...
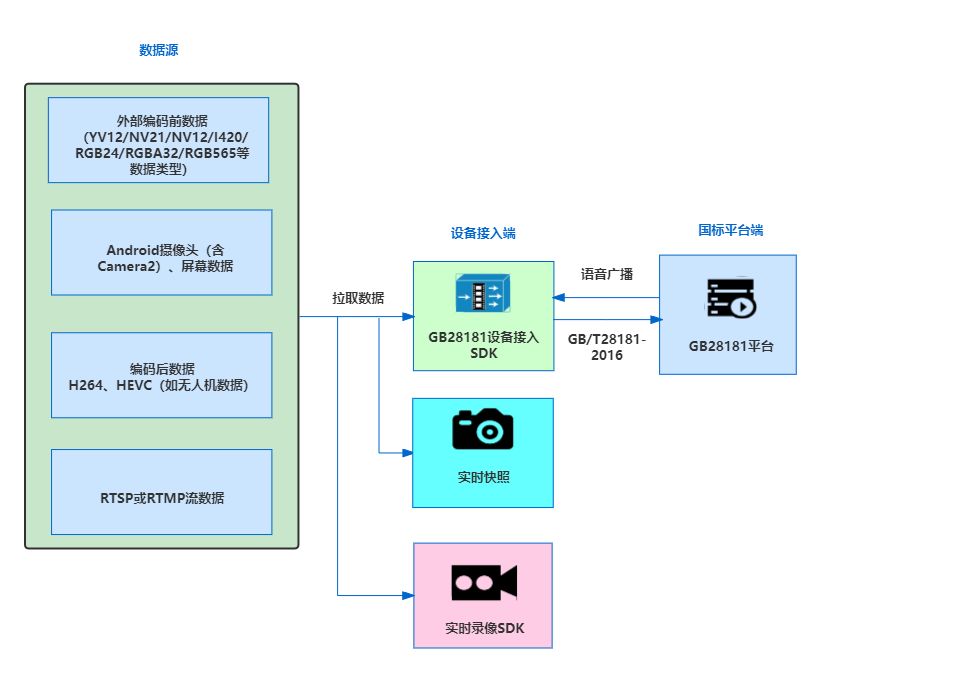
Android平台GB28181设备接入模块之SmartGBD
大牛直播SDK研发的Android平台GB28181设备接入SDK(SmartGBD),可实现不具备国标音视频能力的 Android终端,通过平台注册接入到现有的GB/T28181—2016服务,可用于如执法记录仪、智能安全帽、智能监控、智慧零售、智慧教育…...

JVM第十三讲:调试排错 - JVM 调优参数
调试排错 - JVM 调优参数 本文是JVM第十三讲,调试排错 - JVM 调优参数。对JVM涉及的常见的调优参数和垃圾回收参数进行阐述。 文章目录 调试排错 - JVM 调优参数1、Jvm参数2、垃圾回收 问题1:线上ECS治理问题2:白龙马线上服务机JVM参数配置&a…...

Android Gradle权威指南读书笔记
第一章 Gradle入门 生成Gradle Wrapper 命令:gradle wrapper --gradle-version 版本号自定义Gradle Wrapper task wrapper(type : Wrapper) { gradleVersion 2.4 archiveBase GRADLE USER HOME archivePath wrapper/dists distributionBase GRADLE USER HOME …...
)
顺子日期(蓝桥杯)
文章目录 顺子日期问题描述答案:14字符串解题CC语言指针C语言函数 数组解题 顺子日期 问题描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小明特别喜欢顺子。顺子指的就是连续的三个数字:123、…...
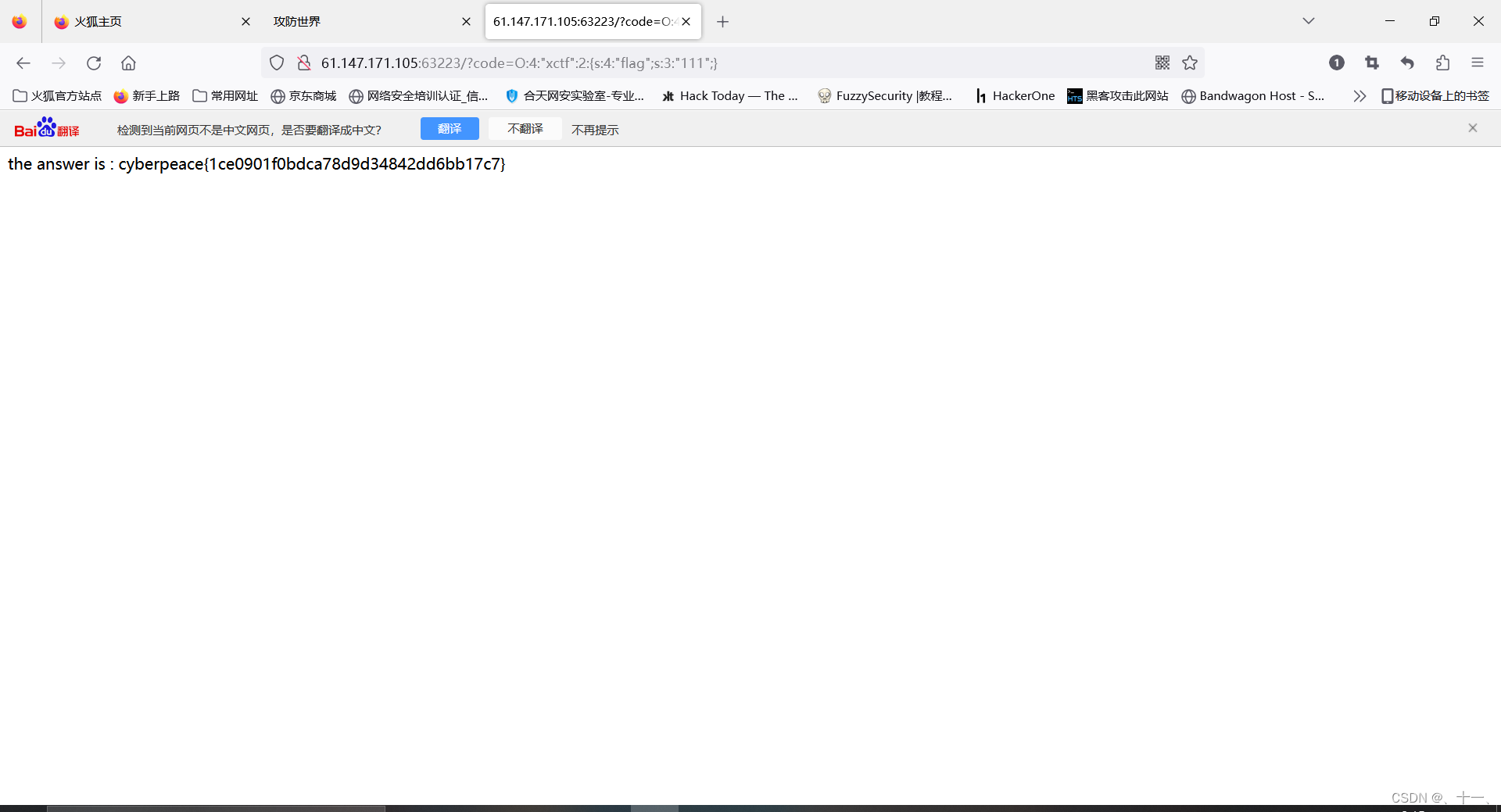
攻防世界web篇-unserialize3
得出php代码残篇 将代码补全后再在线php运行工具中进行运行 在浏览器输入后得到下面的界面 这里需要将O:4:“xctf”:1:{s:4:“flag”;s:3:“111”;} 改为 O:4:“xctf”:2:{s:4:“flag”;s:3:“111”;}...

微信小程序 onLoad和onShow的区别
在微信小程序中,onLoad() 和 onShow() 是两个常用的生命周期函数,用于监听页面的加载和显示事件。这两个函数的区别如下: 触发时机 onLoad() 函数只会在页面加载时触发一次,而 onShow() 函数每次页面显示时都会被触发。因此&#…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
