LeetCode算法刷题(python) Day41|09动态规划|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
目录
- 动规五部曲
- LeetCode 509. 斐波那契数
- LeetCode 70. 爬楼梯
- LeetCode 746. 使用最小花费爬楼梯
动规五部曲
- 确定dp数组以及下标的含义
- 确定递归公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
LeetCode 509. 斐波那契数
力扣题目链接
本题最直观是用递归方法
class Solution:def fib(self, n: int) -> int:if n == 0: return 0elif n == 1: return 1else:return self.fib(n-1) + self.fib(n-2)
当然,本题也可以用动态规划,是最简单的问题
class Solution:def fib(self, n: int) -> int:dp = [0] * (n+1)if n > 0:dp[1] = 1for i in range(2, n+1):dp[i] = dp[i-1] + dp[i-2]return dp[-1]
LeetCode 70. 爬楼梯
力扣题目链接
本题代码实际跟上一题斐波那契数一样。
如果是1个台阶,只有一种方法,如果有两个台阶也只有两种方法,这就是动规的初始值。
当n>2时,到达第n个台阶的最后一步可以爬1个台阶也可以爬2个台阶,如果爬1个台阶,那么前面的种数就跟n-1个台阶的情况一样;如果爬2个台阶,那么跟n-2个台阶的情况一样。
所以n个台阶的方法=n-1个台阶的方法数+n-2个台阶的方法数。这不就是不同初始值的斐波那契数列吗!
class Solution:def climbStairs(self, n: int) -> int:if n <= 2:return ndp = [0] * ndp[0] = 1dp[1] = 2for i in range(2, n):dp[i] = dp[i-1] + dp[i-2]return dp[-1]
LeetCode 746. 使用最小花费爬楼梯
力扣题目链接
- 确定dp数组以及下标的含义:到达第i个台阶的最小花费
- 确定递归公式:
dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]) - dp数组如何初始化:可以从下标为 0 或下标为 1 的台阶开始爬楼梯,意味着
dp[0], dp[1]初始值都为0 - 确定遍历顺序:从前向后遍历
- 举例推导dp数组
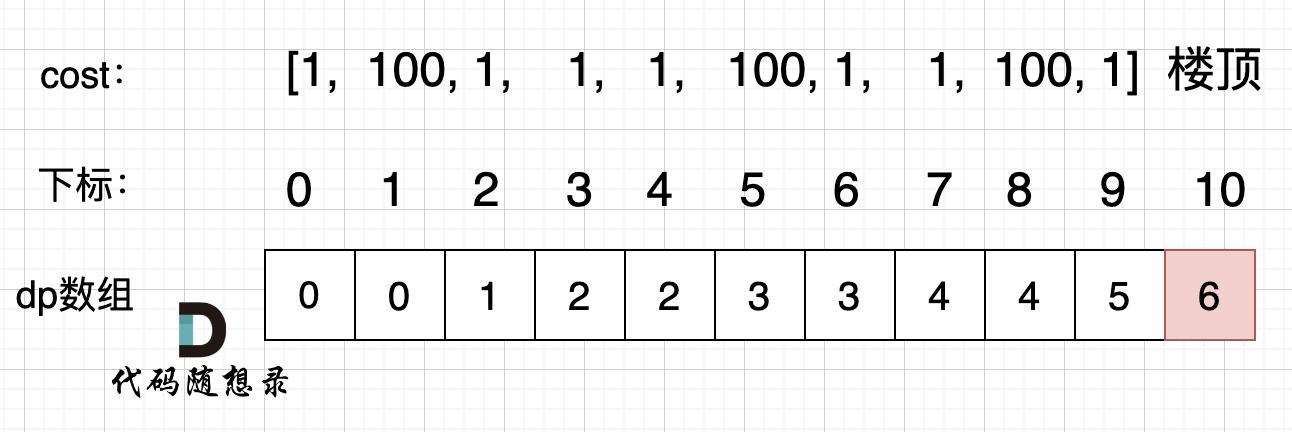
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:dp = [0] * (len(cost) + 1)for i in range(2, len(cost)+1):dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])return dp[-1]
今日毕!
相关文章:

LeetCode算法刷题(python) Day41|09动态规划|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
目录 动规五部曲LeetCode 509. 斐波那契数LeetCode 70. 爬楼梯LeetCode 746. 使用最小花费爬楼梯 动规五部曲 确定dp数组以及下标的含义确定递归公式dp数组如何初始化确定遍历顺序举例推导dp数组 LeetCode 509. 斐波那契数 力扣题目链接 本题最直观是用递归方法 class Sol…...
Spring(四)
1、Spring6整合JUnit 1、JUnit4 User类: package com.songzhishu.spring.bean;import org.springframework.beans.factory.annotation.Value; import org.springframework.stereotype.Component;/*** BelongsProject: Spring6* BelongsPackage: com.songzhishu.spring.bean*…...
)
2023-10-8讯飞大模型部署2024秋招后端一面(附详解)
1 mybatis的mapper是什么东西 在MyBatis中,mapper是一个核心概念,它起到了桥梁的作用,连接Java对象和数据库之间的数据。具体来说,mapper可以分为以下两个部分: Mapper XML文件: 这是一个XML文件ÿ…...
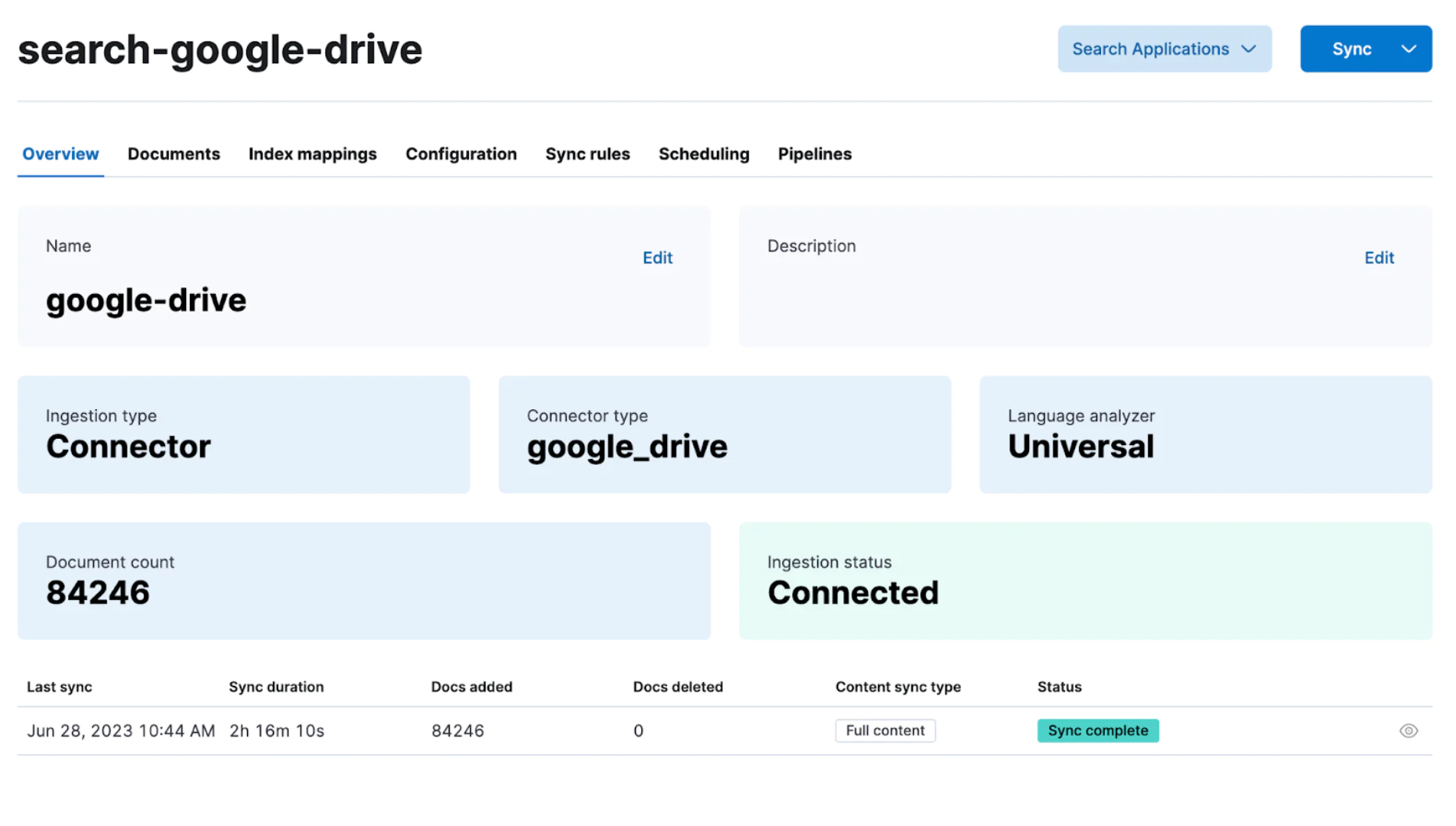
如何为 Elasticsearch 创建自定义连接器
了解如何为 Elasticsearch 创建自定义连接器以简化数据摄取过程。 作者:JEDR BLASZYK Elasticsearch 拥有一个摄取工具库,可以从多个来源获取数据。 但是,有时你的数据源可能与 Elastic 现有的提取工具不兼容。 在这种情况下,你可…...

Debian11 安装 OpenJDK8
1. 下载安装包 wget http://snapshot.debian.org/archive/debian-security/20220210T090326Z/pool/updates/main/o/openjdk-8/openjdk-8-jdk_8u322-b06-1~deb9u1_amd64.deb wget http://snapshot.debian.org/archive/debian-security/20220210T090326Z/pool/updates/main/o/op…...
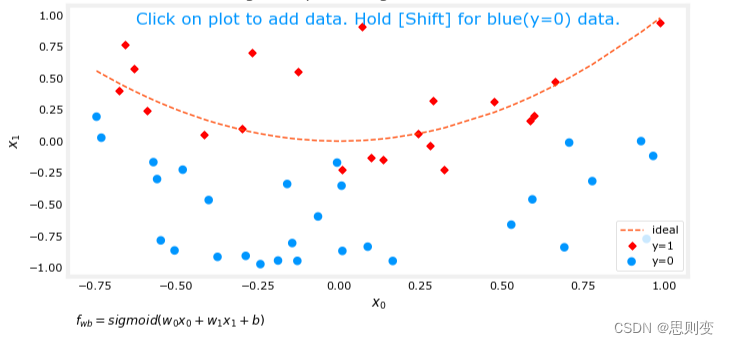
[Machine Learning][Part 6]Cost Function代价函数和梯度正则化
目录 拟合 欠拟合 过拟合 正确的拟合 解决过拟合的方法:正则化 线性回归模型和逻辑回归模型都存在欠拟合和过拟合的情况。 拟合 来自百度的解释: 数据拟合又称曲线拟合,俗称拉曲线,是一种把现有数据透过数学方法来代入一条…...

工业自动化编程与数字图像处理技术
工业自动化编程与数字图像处理技术 编程是计算机领域的基础技能,对于从事软件开发和工程的人来说至关重要。在工业自动化领域,C/C仍然是主流的编程语言,特别是用于工业界面(GUI)编程。工业界面是供车间操作员使用的,使用诸如Hal…...

JY61P.C
/** File Name : JY61P.cDescription : attention © Copyright (c) 2020 STMicroelectronics. All rights reserved.This software component is licensed by ST under Ultimate Liberty licenseSLA0044, the “License”; You may not use this file except in complian…...

Go编程:使用 Colly 库下载Reddit网站的图像
概述 Reddit是一个社交新闻网站,用户可以发布各种主题的内容,包括图片。本文将介绍如何使用Go语言和Colly库编写一个简单的爬虫程序,从Reddit网站上下载指定主题的图片,并保存到本地文件夹中。为了避免被目标网站反爬,…...

高性能日志脱敏组件:已支持 log4j2 和 logback 插件
项目介绍 日志脱敏是常见的安全需求。普通的基于工具类方法的方式,对代码的入侵性太强,编写起来又特别麻烦。 sensitive提供基于注解的方式,并且内置了常见的脱敏方式,便于开发。 同时支持 logback 和 log4j2 等常见的日志脱敏…...

一文读懂PostgreSQL中的索引
前言 索引是加速搜索引擎检索数据的一种特殊表查询。简单地说,索引是一个指向表中数据的指针。一个数据库中的索引与一本书的索引目录是非常相似的。 拿汉语字典的目录页(索引)打比方,我们可以按拼音、笔画、偏旁部首等排序的目录…...

windows的批量解锁
场景 场景是我从github上拉了一个c#项目启动的时候报错, 1>C:\Program Files\Microsoft Visual Studio\2022\Community\MSBuild\Current\Bin\amd64\Microsoft.Common.CurrentVersion.targets(3327,5): error MSB3821: 无法处理文件 UI\Forms\frmScriptBuilder.…...

Nginx配置微服务避免actuator暴露
微服务一般在扫漏洞的情况下,需要屏蔽actuator健康检查 # 避免actuator暴露 if ($request_uri ~ "/actuator") { return 403; }...

GEE——在GEE中计算地形位置指数TPI
简介: DEM中的TPI计算是指通过计算每个像元高程与其邻域高程的差值来计算地形位置指数(Topographic Position Index)。TPI 是描述地形起伏度和地形形态的一个重要指标,可以用于地貌分类、土壤侵蚀、植被分布等领域。 地形位置指数(Topographic Position Index,TPI)是用…...

树的基本操作(数据结构)
树的创建 //结构结点 typedef struct Node {int data;struct Node *leftchild;struct Node *rightchild; }*Bitree,BitNode;//初始化树 void Create(Bitree &T) {int d;printf("输入结点(按0为空结点):");scanf("%d",&d);if(d!0){T (Bitree)ma…...

Python复刻游戏《贪吃蛇大作战》
入门教程、案例源码、学习资料、读者群 请访问: python666.cn 大家好,欢迎来到 Crossin的编程教室 ! 曾经有一款小游戏刷屏微信朋友圈,叫做《贪吃蛇大作战》。一个简单到不行的游戏,也不知道怎么就火了,还上…...
SpringCloud之Gateway整合Sentinel服务降级和限流
1.下载Sentinel.jar可以图形界面配置限流和降级规则 地址:可能需要翻墙 下载jar文件 2.引入maven依赖 <!-- spring cloud gateway整合sentinel的依赖--><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-alibaba-s…...
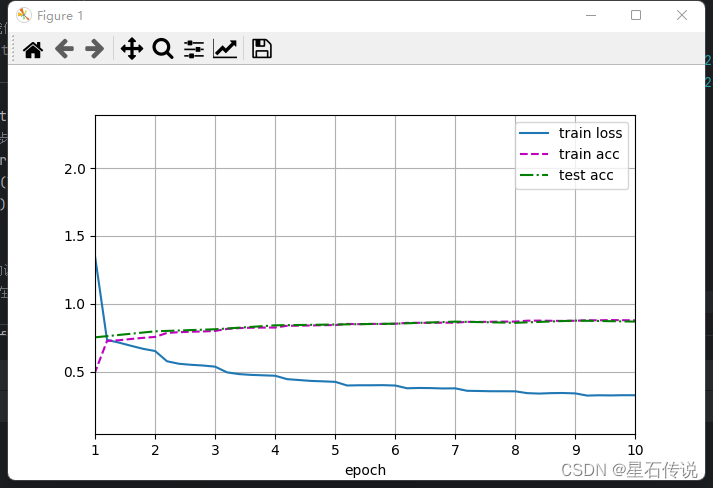
深度学习——深度卷积神经网络(AlexNet)
深度学习——深度卷积神经网络(AlexNet) 文章目录 前言一、学习表征二、AlexNet实现2.1. 模型设计2.2. 激活函数2.3. 容量控制与预处理2.4. 训练模型 总结 前言 在前面学习了卷积神经网络的基本原理,之后将继续学习现代卷积神经网络架构。而本章将学习其…...
提高编程效率-Vscode实用指南
您是否知道全球73%的开发人员依赖同一个代码编辑器? 是的,2023 年 Stack Overflow 开发者调查结果已出炉,Visual Studio Code 迄今为止再次排名第一最常用的开发环境。 “Visual Studio Code 仍然是所有开发人员的首选 IDE,与专业…...

ES 数据库
ES 数据库 通过 API 查询通过 JSON 查询 熟悉 es 的同学都知道 es 一般有两种查询方式 1,在 java 中构建查询对象,调用 es 提供的 api 做查询 2,使用 json 调用接口做查询 查询语句无非是将足够的信息丢给数据库,但是它却和 SQL …...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
