[Machine Learning][Part 6]Cost Function代价函数和梯度正则化
目录
拟合
欠拟合
过拟合
正确的拟合
解决过拟合的方法:正则化
线性回归模型和逻辑回归模型都存在欠拟合和过拟合的情况。
拟合
来自百度的解释:
数据拟合又称曲线拟合,俗称拉曲线,是一种把现有数据透过数学方法来代入一条数式的表示方式。科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合(fitting)。
个人理解,拟合就是根据已有数据来建立的一个数学模型,这个数据模型能最大限度的包含现有的数据。这样预测的数据就能最大程度的符合现有情况。
欠拟合
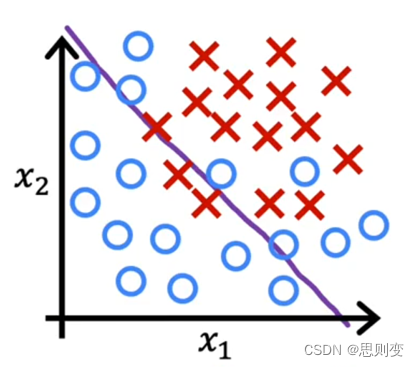
所建立的模型与现有数据匹配度较低如下图的分类模型,决策边界并不能很好的区分目前的数据
当训练数据的特征值较少的时候会出现欠拟合
过拟合
模型过于匹配现有数据,导致模型不能推广应用到更多数据中去。当训练数据的特征值太多的时候会出现这种情况。

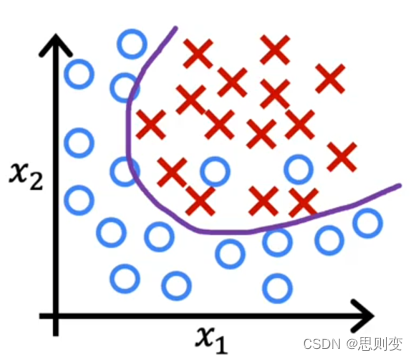
正确的拟合
介于欠拟合和过拟合之间
解决过拟合的方法:正则化
解决过拟合的方法是将模型正则化,就是说把不是主要特征的w_j调整为无限接近于0,然后训练模型,这样来寻找最优的模型。这样存在一个问题,怎么分辨特征是不是主要特征呢?这个是不好分辨的,因此是把所有的特征都正则化,正则化的公式为:
线性回归cost function:
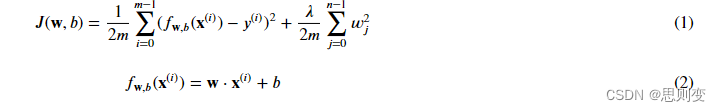
逻辑回归cost function:
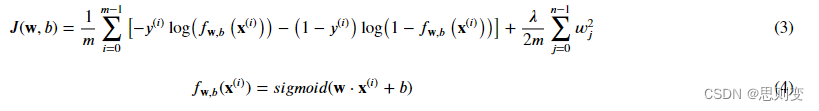
适用于线性回归和逻辑回归的梯度下降函数:
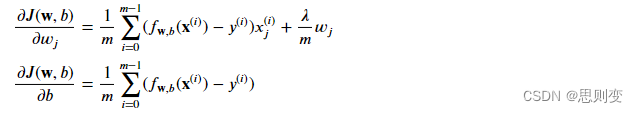
实现代码:
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from plt_overfit import overfit_example, outputnp.set_printoptions(precision=8)def sigmoid(z):"""Compute the sigmoid of zArgs:z (ndarray): A scalar, numpy array of any size.Returns:g (ndarray): sigmoid(z), with the same shape as z"""g = 1/(1+np.exp(-z))return gdef compute_cost_linear_reg(X, y, w, b, lambda_ = 1):"""Computes the cost over all examplesArgs:X (ndarray (m,n): Data, m examples with n featuresy (ndarray (m,)): target valuesw (ndarray (n,)): model parameters b (scalar) : model parameterlambda_ (scalar): Controls amount of regularizationReturns:total_cost (scalar): cost """m = X.shape[0]n = len(w)cost = 0.for i in range(m):f_wb_i = np.dot(X[i], w) + b #(n,)(n,)=scalar, see np.dotcost = cost + (f_wb_i - y[i])**2 #scalar cost = cost / (2 * m) #scalar reg_cost = 0for j in range(n):reg_cost += (w[j]**2) #scalarreg_cost = (lambda_/(2*m)) * reg_cost #scalartotal_cost = cost + reg_cost #scalarreturn total_cost #scalarnp.random.seed(1)
X_tmp = np.random.rand(5,6)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1]).reshape(-1,)-0.5
b_tmp = 0.5
lambda_tmp = 0.7
cost_tmp = compute_cost_linear_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)print("Regularized cost:", cost_tmp)def compute_cost_logistic_reg(X, y, w, b, lambda_ = 1):"""Computes the cost over all examplesArgs:Args:X (ndarray (m,n): Data, m examples with n featuresy (ndarray (m,)): target valuesw (ndarray (n,)): model parameters b (scalar) : model parameterlambda_ (scalar): Controls amount of regularizationReturns:total_cost (scalar): cost """m,n = X.shapecost = 0.for i in range(m):z_i = np.dot(X[i], w) + b #(n,)(n,)=scalar, see np.dotf_wb_i = sigmoid(z_i) #scalarcost += -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i) #scalarcost = cost/m #scalarreg_cost = 0for j in range(n):reg_cost += (w[j]**2) #scalarreg_cost = (lambda_/(2*m)) * reg_cost #scalartotal_cost = cost + reg_cost #scalarreturn total_cost #scalarnp.random.seed(1)
X_tmp = np.random.rand(5,6)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1]).reshape(-1,)-0.5
b_tmp = 0.5
lambda_tmp = 0.7
cost_tmp = compute_cost_logistic_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)print("Regularized cost:", cost_tmp)def compute_gradient_linear_reg(X, y, w, b, lambda_): """Computes the gradient for linear regression Args:X (ndarray (m,n): Data, m examples with n featuresy (ndarray (m,)): target valuesw (ndarray (n,)): model parameters b (scalar) : model parameterlambda_ (scalar): Controls amount of regularizationReturns:dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w. dj_db (scalar): The gradient of the cost w.r.t. the parameter b. """m,n = X.shape #(number of examples, number of features)dj_dw = np.zeros((n,))dj_db = 0.for i in range(m): err = (np.dot(X[i], w) + b) - y[i] for j in range(n): dj_dw[j] = dj_dw[j] + err * X[i, j] dj_db = dj_db + err dj_dw = dj_dw / m dj_db = dj_db / m for j in range(n):dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]return dj_db, dj_dwnp.random.seed(1)
X_tmp = np.random.rand(5,3)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1])
b_tmp = 0.5
lambda_tmp = 0.7
dj_db_tmp, dj_dw_tmp = compute_gradient_linear_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)print(f"dj_db: {dj_db_tmp}", )
print(f"Regularized dj_dw:\n {dj_dw_tmp.tolist()}", )def compute_gradient_logistic_reg(X, y, w, b, lambda_): """Computes the gradient for linear regression Args:X (ndarray (m,n): Data, m examples with n featuresy (ndarray (m,)): target valuesw (ndarray (n,)): model parameters b (scalar) : model parameterlambda_ (scalar): Controls amount of regularizationReturnsdj_dw (ndarray Shape (n,)): The gradient of the cost w.r.t. the parameters w. dj_db (scalar) : The gradient of the cost w.r.t. the parameter b. """m,n = X.shapedj_dw = np.zeros((n,)) #(n,)dj_db = 0.0 #scalarfor i in range(m):f_wb_i = sigmoid(np.dot(X[i],w) + b) #(n,)(n,)=scalarerr_i = f_wb_i - y[i] #scalarfor j in range(n):dj_dw[j] = dj_dw[j] + err_i * X[i,j] #scalardj_db = dj_db + err_idj_dw = dj_dw/m #(n,)dj_db = dj_db/m #scalarfor j in range(n):dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]return dj_db, dj_dw np.random.seed(1)
X_tmp = np.random.rand(5,3)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1])
b_tmp = 0.5
lambda_tmp = 0.7
dj_db_tmp, dj_dw_tmp = compute_gradient_logistic_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)print(f"dj_db: {dj_db_tmp}", )
print(f"Regularized dj_dw:\n {dj_dw_tmp.tolist()}", )plt.close("all")
display(output)
ofit = overfit_example(True)逻辑回归输出为:
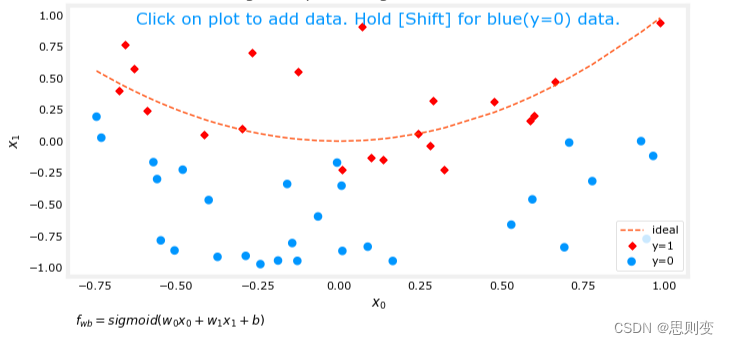
相关文章:

[Machine Learning][Part 6]Cost Function代价函数和梯度正则化
目录 拟合 欠拟合 过拟合 正确的拟合 解决过拟合的方法:正则化 线性回归模型和逻辑回归模型都存在欠拟合和过拟合的情况。 拟合 来自百度的解释: 数据拟合又称曲线拟合,俗称拉曲线,是一种把现有数据透过数学方法来代入一条…...

工业自动化编程与数字图像处理技术
工业自动化编程与数字图像处理技术 编程是计算机领域的基础技能,对于从事软件开发和工程的人来说至关重要。在工业自动化领域,C/C仍然是主流的编程语言,特别是用于工业界面(GUI)编程。工业界面是供车间操作员使用的,使用诸如Hal…...

JY61P.C
/** File Name : JY61P.cDescription : attention © Copyright (c) 2020 STMicroelectronics. All rights reserved.This software component is licensed by ST under Ultimate Liberty licenseSLA0044, the “License”; You may not use this file except in complian…...

Go编程:使用 Colly 库下载Reddit网站的图像
概述 Reddit是一个社交新闻网站,用户可以发布各种主题的内容,包括图片。本文将介绍如何使用Go语言和Colly库编写一个简单的爬虫程序,从Reddit网站上下载指定主题的图片,并保存到本地文件夹中。为了避免被目标网站反爬,…...

高性能日志脱敏组件:已支持 log4j2 和 logback 插件
项目介绍 日志脱敏是常见的安全需求。普通的基于工具类方法的方式,对代码的入侵性太强,编写起来又特别麻烦。 sensitive提供基于注解的方式,并且内置了常见的脱敏方式,便于开发。 同时支持 logback 和 log4j2 等常见的日志脱敏…...

一文读懂PostgreSQL中的索引
前言 索引是加速搜索引擎检索数据的一种特殊表查询。简单地说,索引是一个指向表中数据的指针。一个数据库中的索引与一本书的索引目录是非常相似的。 拿汉语字典的目录页(索引)打比方,我们可以按拼音、笔画、偏旁部首等排序的目录…...

windows的批量解锁
场景 场景是我从github上拉了一个c#项目启动的时候报错, 1>C:\Program Files\Microsoft Visual Studio\2022\Community\MSBuild\Current\Bin\amd64\Microsoft.Common.CurrentVersion.targets(3327,5): error MSB3821: 无法处理文件 UI\Forms\frmScriptBuilder.…...

Nginx配置微服务避免actuator暴露
微服务一般在扫漏洞的情况下,需要屏蔽actuator健康检查 # 避免actuator暴露 if ($request_uri ~ "/actuator") { return 403; }...

GEE——在GEE中计算地形位置指数TPI
简介: DEM中的TPI计算是指通过计算每个像元高程与其邻域高程的差值来计算地形位置指数(Topographic Position Index)。TPI 是描述地形起伏度和地形形态的一个重要指标,可以用于地貌分类、土壤侵蚀、植被分布等领域。 地形位置指数(Topographic Position Index,TPI)是用…...

树的基本操作(数据结构)
树的创建 //结构结点 typedef struct Node {int data;struct Node *leftchild;struct Node *rightchild; }*Bitree,BitNode;//初始化树 void Create(Bitree &T) {int d;printf("输入结点(按0为空结点):");scanf("%d",&d);if(d!0){T (Bitree)ma…...

Python复刻游戏《贪吃蛇大作战》
入门教程、案例源码、学习资料、读者群 请访问: python666.cn 大家好,欢迎来到 Crossin的编程教室 ! 曾经有一款小游戏刷屏微信朋友圈,叫做《贪吃蛇大作战》。一个简单到不行的游戏,也不知道怎么就火了,还上…...
SpringCloud之Gateway整合Sentinel服务降级和限流
1.下载Sentinel.jar可以图形界面配置限流和降级规则 地址:可能需要翻墙 下载jar文件 2.引入maven依赖 <!-- spring cloud gateway整合sentinel的依赖--><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-alibaba-s…...
深度学习——深度卷积神经网络(AlexNet)
深度学习——深度卷积神经网络(AlexNet) 文章目录 前言一、学习表征二、AlexNet实现2.1. 模型设计2.2. 激活函数2.3. 容量控制与预处理2.4. 训练模型 总结 前言 在前面学习了卷积神经网络的基本原理,之后将继续学习现代卷积神经网络架构。而本章将学习其…...
提高编程效率-Vscode实用指南
您是否知道全球73%的开发人员依赖同一个代码编辑器? 是的,2023 年 Stack Overflow 开发者调查结果已出炉,Visual Studio Code 迄今为止再次排名第一最常用的开发环境。 “Visual Studio Code 仍然是所有开发人员的首选 IDE,与专业…...

ES 数据库
ES 数据库 通过 API 查询通过 JSON 查询 熟悉 es 的同学都知道 es 一般有两种查询方式 1,在 java 中构建查询对象,调用 es 提供的 api 做查询 2,使用 json 调用接口做查询 查询语句无非是将足够的信息丢给数据库,但是它却和 SQL …...

面试经典150题——Day14
文章目录 一、题目二、题解 一、题目 134. Gas Station There are n gas stations along a circular route, where the amount of gas at the ith station is gas[i]. You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from the ith stati…...

Pika v3.5.1发布!
Pika 社区很高兴宣布,我们今天发布已经过我们生产环境验证 v3.5.1 版本,https://github.com/OpenAtomFoundation/pika/releases/tag/v3.5.1 。 该版本不仅做了很多优化工作,还引入了多项新功能。这些新功能包括 动态关闭 WAL、ReplicationID…...

Kotlin中的数组
数组是一种常见的数据结构,用于存储相同类型的多个元素。在 Kotlin 中,我们可以使用不同的方式声明、初始化和操作数组。 在 Kotlin 中,有多种方式可以定义和操作数组。我们将通过以下示例代码来展示不同的数组操作: fun main()…...
(3) OpenCV图像处理kNN近邻算法-识别摄像头数字
目录 一、代码简介 二、程序代码 三、使用的图片资源 1、图片digits.png...

上海亚商投顾:沪指震荡调整 转基因概念股逆势大涨
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 沪指昨日低开低走,深成指、创业板指均跌超1%,双双创出年内新低。转基因概念股逆势大涨…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
