第十三届蓝桥杯国赛 C++ B 组 J 题——搬砖(AC)
目录
- 1.搬砖
- 1.题目描述
- 2.输入格式
- 3.输出格式
- 4.样例输入
- 5.样例输出
- 6.数据范围
- 7.原题链接
- 2.解题思路
- 3.Ac_code
1.搬砖
1.题目描述
这天,小明在搬砖。
他一共有 nnn 块砖, 他发现第 iii 砖的重量为 wiw_{i}wi, 价值为 viv_{i}vi 。他突然想从这些 砖中选一些出来从下到上堆成一座塔, 并且对于塔中的每一块砖来说, 它上面 所有砖的重量和不能超过它自身的价值。
他想知道这样堆成的塔的总价值(即塔中所有砖块的价值和)最大是多少。
2.输入格式
输入共 n+1n+1n+1 行, 第一行为一个正整数 nnn, 表示砖块的数量。后面 nnn 行, 每行两个正整数 wi,viw_i ,v_iwi,vi
分别表示每块砖的重量和价值。
3.输出格式
一行, 一个整数表示答案。
4.样例输入
5
4 4
1 1
5 2
5 5
4 3
5.样例输出
10
6.数据范围
n≤1000;wi≤20;vi≤20000。n≤1000;w_i ≤20;v_i ≤20000 。n≤1000;wi≤20;vi≤20000。
7.原题链接
搬砖
2.解题思路
诸如此题的模型,思路都是按照一种方式排序,使得最优解答案的选择情况,是排序后的一个子序列,然后直接进行背包 dpdpdp 即可。
那么该如何去寻找排序的条件呢?一般的思路在于,对于砖块 xxx 和 yyy,如果排序后的结果 yyy 在 xxx的后面,那么对于任意 yyy 在 xxx 之上的摆放情况,都一定可以将两者调换。
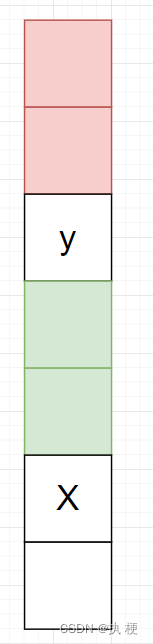
如图,红色砖块为 yyy 上所有砖块的重量,我们设为 w1w_1w1,绿色为 xxx 与 yyy 之间的砖块重量,我们设为 w2w_2w2。
根据题意可知:vy≥w1,vx≥w1+wy+w2v_y≥ w_1,v_x≥w_1+w_y+w_2vy≥w1,vx≥w1+wy+w2,1
假设排序后 yyy 在 xxx 的后面,那么也一定满足:vx≥w1,vy≥w1+wx+w2v_x≥ w_1,v_y≥w_1+w_x+w_2vx≥w1,vy≥w1+wx+w22
因为vx≥w1+wy+w2v_x≥w_1+w_y+w_2vx≥w1+wy+w21且wy+w2w_y+w_2wy+w2一定大于 000,显然vx≥w1v_x≥ w_1vx≥w1是一定符合要求的。
然后考虑第二个式子,因为 vx≥w1+wy+w2v_x≥w_1+w_y+w_2vx≥w1+wy+w21,经过变形可得 vx−wy≥w1+w2v_x-w_y≥w_1+w_2vx−wy≥w1+w23
将式子3带入式子2可得:
vy≥wx+vx−wyv_y≥w_x+v_x-w_yvy≥wx+vx−wy
将式子整理可得:
vy+wy≥wx+vxv_y+w_y≥w_x+v_xvy+wy≥wx+vx
由此,我们找到了排序条件,也就是说,当满足 vy+wy≥wx+vxv_y+w_y≥w_x+v_xvy+wy≥wx+vx 时,任意 yyy 在 xxx 之上的摆放情况,都一定可以将两者调换
接下来就是进行背包 dpdpdp即可,
定义 f[i][j]f[i][j]f[i][j]为只考虑前 iii 个物品,且选择的重量为 jjj 的最大价值。考虑如何进行转移,对于背包问题,无非是选与不选的两种抉择:
f[i][j]={f[i−1][j]不可选max(f[i−1][j],f[i−1][j−w]+v)if j≥w且v≥j-w可选f[i][j] = \begin{cases} f[i-1][j] &不可选\\ max(f[i-1][j],f[i-1][j-w]+v) &\text{if j≥w且v≥j-w} 可选\\ \end{cases}f[i][j]={f[i−1][j]max(f[i−1][j],f[i−1][j−w]+v)不可选if j≥w且v≥j-w可选
题目体积最大只有2e4,答案即为从f[n][0]f[n][0]f[n][0]到 f[n][20000]f[n][20000]f[n][20000]取个最大值。由于是01背包问题,可以使用滚动数组进行优化。
时间复杂度:O(nlogn+nV)O(nlogn+nV)O(nlogn+nV)
3.Ac_code
未优化版本:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 1010;int n;
//只考虑前 i 个砖块,且重量为 j 的最大价值
int f[N][N * 20];
PII a[N];
bool cmp(PII b, PII c) {return b.first + b.second < c.first + c.second;
}
void solve()
{cin >> n;for (int i = 1; i <= n; ++i) {cin >> a[i].first >> a[i].second;}sort(a + 1, a + n + 1, cmp);for (int i = 1; i <= n; ++i) {int w = a[i].first, v = a[i].second;for (int j = 0; j <= 20000; ++j) {f[i][j] = f[i - 1][j];//可选情况if (w <= j && v >= j - w) f[i][j] = max(f[i][j], f[i - 1][j - w] + v);}}int ans=0;for(int i=0;i<=20000;++i) ans=max(ans,f[n][i]);cout << ans << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
滚动数组优化:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 1010;int n;
//只考虑前 i 个砖块,且重量为 j 的最大价值
int f[N * 20];
PII a[N];
bool cmp(PII b, PII c) {return b.first + b.second < c.first + c.second;
}
void solve()
{cin >> n;for (int i = 1; i <= n; ++i) {cin >> a[i].first >> a[i].second;}sort(a + 1, a + n + 1, cmp);for (int i = 1; i <= n; ++i) {int w = a[i].first, v = a[i].second;for (int j = 20000; j >= w; --j) {//可选情况if ( v >= j - w) f[j] = max(f[j], f[j - w] + v);}}int ans = 0;for (int i = 0; i <= 20000; ++i) ans = max(ans, f[i]);cout << ans << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}相关文章:

第十三届蓝桥杯国赛 C++ B 组 J 题——搬砖(AC)
目录1.搬砖1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路3.Ac_code1.搬砖 1.题目描述 这天,小明在搬砖。 他一共有 nnn 块砖, 他发现第 iii 砖的重量为 wiw_{i}wi, 价值为 viv_{i}vi 。他突然想从这些 砖中选一些出来从…...
- Nacos服务端服务发现处理)
Spring Cloud Nacos源码讲解(十)- Nacos服务端服务发现处理
Nacos集群数据同步 当我们有服务进行注册以后,会写入注册信息同时会触发ClientChangedEvent事件,通过这个事件,就会开始进行Nacos的集群数据同步,当然这其中只有有一个Nacos节点来处理对应的客户端请求,其实这其中…...
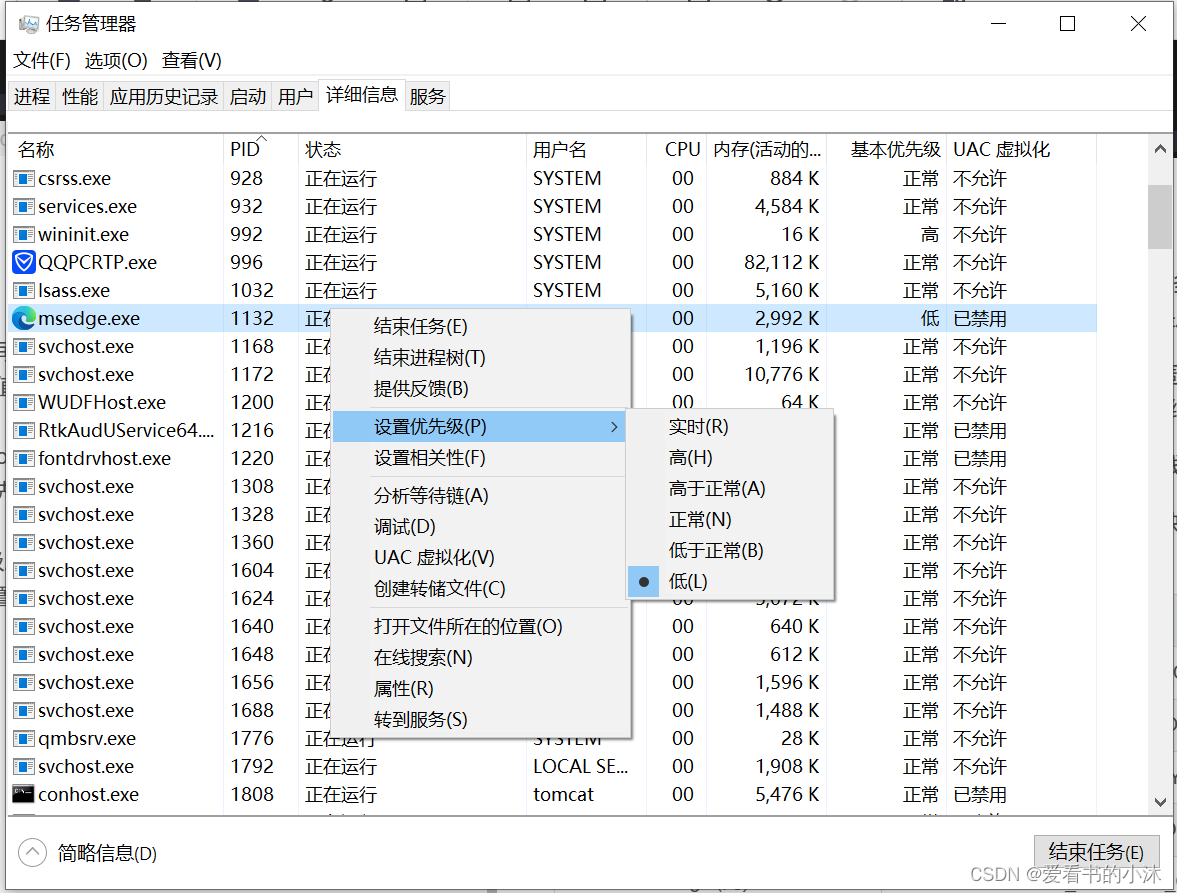
C++ 修改程序进程的优先级(Linux,Windows)
文章目录1、Linux1.1 常用命令1.1.1 不占用终端运行和后台运行方式1.1.2 查询进程1.1.3 结束进程1.1.4 优先级命令1.2 C 代码示例1.2.1 代码一1.2.2 代码二2、Windows2.1 简介2.2 函数声明2.3 C 代码示例2.3.1 代码一2.3.2 代码二结语1、Linux 1.1 常用命令 1.1.1 不占用终端…...
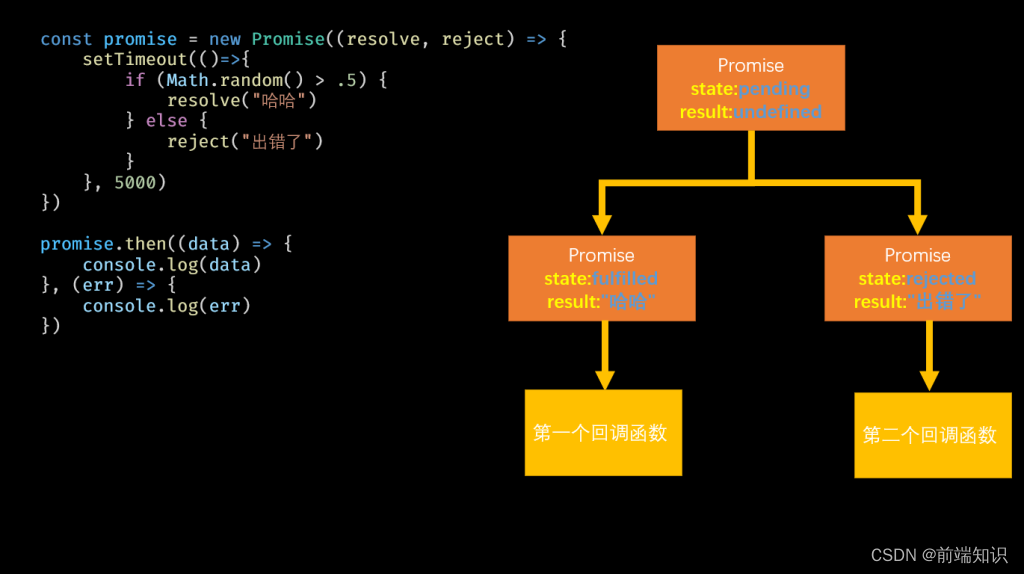
同步和异步promise
进程和线程进程(厂房):程序的运行环境线程(工人):进行运算的东西同步和异步同步:一件事干完才去干下一件事,前面的代码不执行,后面的代码也不执行。同步的代码可能会出现…...
CHATGPT是新的“搜索引擎终结者”吗?百度是否慌了
ChatGPT 以其非凡的自然语言处理 (NLP) 能力和清晰的响应风靡全球,有望带来一场重大的技术革命。在不知不觉中,叙事转向了ChatGPT与百度的对决,因为来自OpenAI的智能和健谈的聊天机器人已经慢慢获得了“潜在的百度终结…...

力扣-订单最多的客户
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:586. 订单最多的客户二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总…...
MyBatis学习笔记(六) —— MyBatis的各种查询功能
6、MyBatis的各种查询功能 6.1、查询一个实体类对象 SelectMapper.java接口 /*** 根据用户id查询用户信息* param id* return*/ User getUserById(Param("id") int id);SelectMapper.xml <!--User getUserById(Param("id") int id)--> <selec…...
2023年最新详细教程!手把手教你搭建Hexo + GitLab个人博客
文章目录前言一、安装和配置环境1.安装 Git2.安装 Node.js二、新建博客项目1.GitLab配置CI/CD自动化部署1.1 GitLab新建项目1.2 GitLab自建Runners1.2.1 下载gitlab-runner1.2.2 注册Runners1.2.3 安装Runners并启动1.3 添加.gitlab-ci.yml文件2.拉取和推送hexo blog2.1 拉取he…...
centos7安装
centos7安装制作U盘启动盘下载镜像下载 UltralISO制作启动盘使用U盘安装系统修改模式为 UEFI调整BOOT option保存重启进入安装界面安装图形界面安装搜狗输入法制作U盘启动盘 下载镜像 去官网下载镜像,找到 mirrors链接(速度快) 选择一个中…...

java String类(超详细,含常用方法、面试题,内存图,案例)
String类一、String类的特点二、String 类的常见构造方法三、String常见的面试题1.字符串常量池2.String s "abc"与String s new String("abc")区别3.字符拼接4.常量优化机制四、String常用方法1. 比较字符串内容2. 遍历字符串3.截取字符串4.替换字符串5…...
哈希表以及哈希冲突
目录 哈希表 哈希冲突 1. 冲突发生 2. 比较常见的哈希函数 3. 负载因子调节(重点) 散列表的载荷因子概念 负载因子和冲突率的关系 冲突-解决-闭散列 线性探测 二次探测 冲突-解决-开散列 结尾 我们在前面讲解了TerrMap(Set)的底层是一个搜索…...
测试——基本概念
概念 测试和调试有以下几点区别: 测试是测试人员进行的工作,调试是开发人员调试是发现并解决问题,测试只是发现问题测试贯穿于整个项目的生命周期,而调试主要在编码阶段 测试人员一般有如下的工作: 需求分析&#x…...
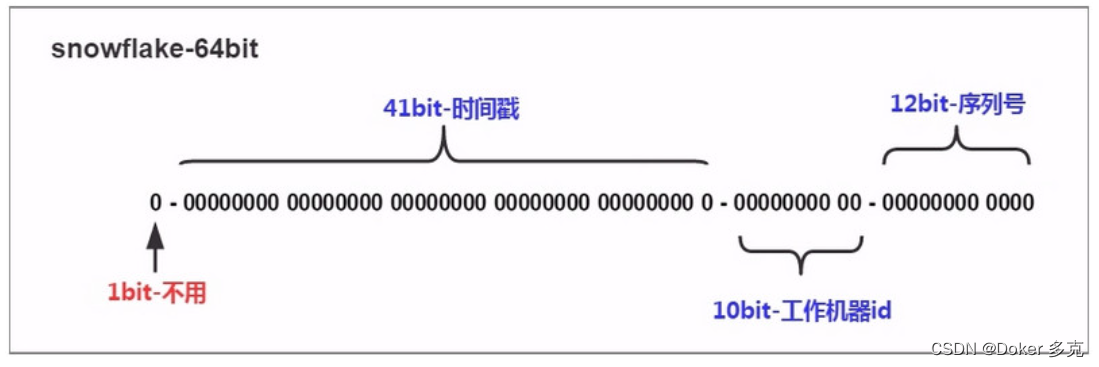
SnowFlake 雪花算法和原理(分布式 id 生成算法)
一、概述 SnowFlake 算法:是 Twitter 开源的分布式 id 生成算法。核心思想:使用一个 64 bit 的 long 型的数字作为全局唯一 id。算法原理最高位是符号位,始终为0,不可用。41位的时间序列,精确到毫秒级,41位…...
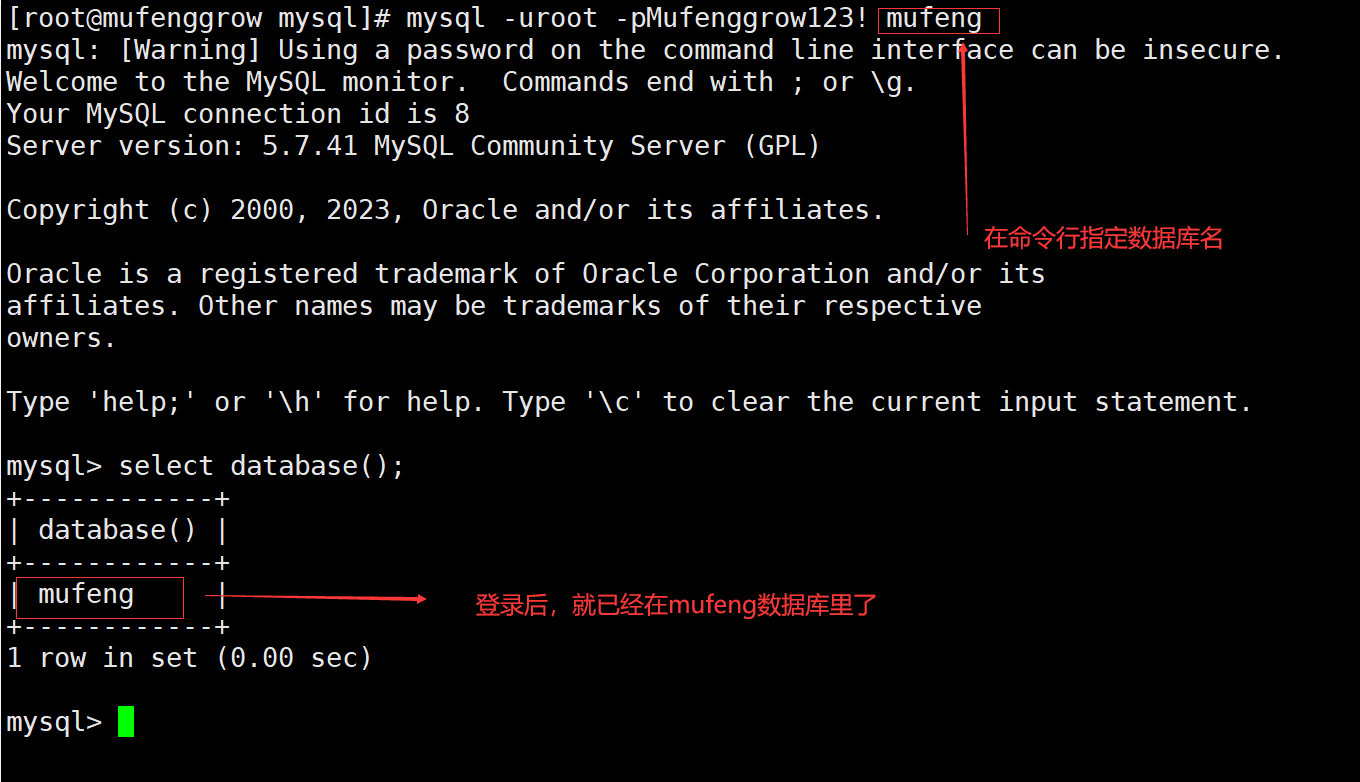
【死磕数据库专栏】MySQL对数据库增删改查的基本操作
前言 本文是专栏【死磕数据库专栏】的第二篇文章,主要讲解MySQL语句最常用的增删改查操作。我一直觉得这个世界就是个程序,每天都在执行增删改查。 MySQL 中我们最常用的增删改查,对应SQL语句就是 insert 、delete、update、select…...
阿里软件测试二面:adb 连接 Android 手机的两种方式,看完你就懂了
前言 随着现在移动端技术的突飞猛进,导致现在市场上,APP 应用数不胜数,那对于测试工程师而言,对于 APP 的测试,那基本就是一个必修课了。 今天,我就来给大家介绍一下,adb 连接 Android 手机的两…...
Docker安装YApi
目录0、Docker 环境准备1、数据库准备 MongoDB2、启动 YAPI3、官网教程0、Docker 环境准备 Docker 容器之间网络互通需要使用 docker network create yapi 创建一个自定义网络 docker network create yapi1、数据库准备 MongoDB YAPI 的数据库是 MongoDB,准备镜像…...

springboot自定义参数解析器
为什么要自定义参数解析器呢? 因为很多项目每次获取用户信息,需要重复从请求头中获取token,用token再去redis或是sql中去拿到存储的计本对象,再将获取到的Json数据,转化为我们需要的对象等代码,作为一名程…...

Python Unittest ddt数据驱动
1、数据驱动介绍: ddt.ddt(类装饰器,申明当前类使用ddt框架)ddt.data(函数装饰器,用于给测试用例传递数据),支持传python所有数据类型:数字(int,…...

Vue自定义组件遇到分页传输数据不正确解决办法
测试环境 Vue3 Element Plus 遇到问题 <el-table:data"tableData">...其他el-table-column<template #default"scope">// 自定义组件<my-button name"编辑" :id"scope.row.id"/ ></template></el-table&…...

ABAP 辨析CO|CN|CA|NA|CS|NS|CP|NP
1、文档说明 本篇文档将通过举例,解析字符的比较运算符之间的用法和区别,涉及到的操作符:CO|CN|CA|NA|CS|NS|CP|NP 2、用法和区别 用法总览 以下举例,几乎都使用一个字符变量和一个硬编码字符进行对比的方式,忽略尾…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
