Leetcode 第 365 场周赛题解
Leetcode 第 365 场周赛题解
- Leetcode 第 365 场周赛题解
- 题目1:2873. 有序三元组中的最大值 I
- 思路
- 代码
- 复杂度分析
- 题目2:2874. 有序三元组中的最大值 II
- 思路
- 代码
- 复杂度分析
- 思路2
- 题目3:2875. 无限数组的最短子数组
- 思路
- 代码
- 复杂度分析
- 题目4:2876. 有向图访问计数
Leetcode 第 365 场周赛题解
题目1:2873. 有序三元组中的最大值 I
思路
暴力。
代码
/** @lc app=leetcode.cn id=2873 lang=cpp** [2873] 有序三元组中的最大值 I*/// @lc code=start
class Solution
{
public:long long maximumTripletValue(vector<int> &nums){int n = nums.size();long long ans = INT_MIN;for (int i = 0; i < n - 2; i++)for (int j = i + 1; j < n - 1; j++)for (int k = j + 1; k < n; k++)ans = max(ans, (long long)(nums[i] - nums[j]) * nums[k]);return ans >= 0 ? ans : 0;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n3),其中 n 是数组 nums 的长度。
空间复杂度:O(1)。
题目2:2874. 有序三元组中的最大值 II
思路
枚举 k,我们需要知道 k 左边 nums[i]−nums[j] 的最大值。
使用 pre_max 维护 k 之前的 nums[i] 的最大值,使用 max_diff 维护 nums[i]−nums[j] 的最大值。
每次遍历一个 nums[i],都更新 ans,pre_max,max_diff:
- ans = max(ans, (long long)max_diff * nums[i])
- max_diff = max(max_diff, pre_max - nums[i])
- pre_max = max(pre_max, nums[i])
最后 return ans >= 0 ? ans : 0 即为答案。
代码
/** @lc app=leetcode.cn id=2874 lang=cpp** [2874] 有序三元组中的最大值 II*/// @lc code=start
class Solution
{
public:long long maximumTripletValue(vector<int> &nums){int n = nums.size();long long ans = INT_MIN;int max_diff = 0, pre_max = 0;for (int i = 0; i < n; i++){ans = max(ans, (long long)max_diff * nums[i]);max_diff = max(max_diff, pre_max - nums[i]);pre_max = max(pre_max, nums[i]);}return ans >= 0 ? ans : 0;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n),其中 n 是数组 nums 的长度。
空间复杂度:O(1)。
思路2
枚举 j
pre_max 数组维护 nums[i] 的最大值。
max_suffix 数组维护 nums[k] 的最大值。
更新 ans = max(ans, (long long)(pre_max[j - 1] - nums[j]) * max_suffix[j + 1])。
最后 return ans >= 0 ? ans : 0 即为答案。
class Solution
{
public:long long maximumTripletValue(vector<int> &nums){int n = nums.size();long long ans = INT_MIN;vector<int> pre_max(n, 0);pre_max[0] = nums[0];for (int i = 1; i < n; i++)pre_max[i] = max(pre_max[i - 1], nums[i]);vector<int> max_suffix(n, 0);max_suffix[n - 1] = nums[n - 1];for (int i = n - 2; i >= 0; i--)max_suffix[i] = max(max_suffix[i + 1], nums[i]);for (int j = 1; j < n - 1; j++)ans = max(ans, (long long)(pre_max[j - 1] - nums[j]) * max_suffix[j + 1]);return ans >= 0 ? ans : 0;}
};
题目3:2875. 无限数组的最短子数组
思路
滑动窗口。
设数组 nums 的总和为 total,长度为 n。
已知数组 infinite_nums 是通过无限地将 nums 的元素追加到自己之后生成的。
假设有下面这种情况:

去掉中间一整段完整的 nums 数组,新的目标值为 target % total。
问题转化为在 nums + nums[1,…,n-1] 这个长度为 2 * n - 1 的数组上,求满足元素和 等于 target % total 的最短子数组,设这个长度为 len。
加上 target / total 个完整数组的长度,最终的长度为 len + target / total * n。
代码
/** @lc app=leetcode.cn id=2875 lang=cpp** [2875] 无限数组的最短子数组*/// @lc code=start// 滑动窗口class Solution
{
public:int minSizeSubarray(vector<int> &nums, int target){int n = nums.size();long long total = accumulate(nums.begin(), nums.end(), 0LL);for (int i = 0; i < n - 1; i++)nums.push_back(nums[i]);long long sum = 0;int left = 0, len = INT_MAX;for (int right = 0; right < 2 * n - 1; right++){sum += nums[right];while (sum > target % total){sum -= nums[left];left++;}int cur_len = right - left + 1;if (sum == target % total)len = min(len, cur_len);}return len == INT_MAX ? -1 : len + target / total * n;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n),其中 n 为 nums 数组的长度。
空间复杂度:O(n),延长了 nums 数组。
题目4:2876. 有向图访问计数
超出能力范围。
题解:【模板】内向基环树
相关文章:

Leetcode 第 365 场周赛题解
Leetcode 第 365 场周赛题解 Leetcode 第 365 场周赛题解题目1:2873. 有序三元组中的最大值 I思路代码复杂度分析 题目2:2874. 有序三元组中的最大值 II思路代码复杂度分析思路2 题目3:2875. 无限数组的最短子数组思路代码复杂度分析 题目4&a…...

什么是软件测试? 软件测试都有什么岗位 ?软件测试和调试的区别? 软件测试和开发的区别?软件测试等相关概念入门篇
1、什么是软件测试? 常见理解: 软件测试就是找BUG,发现缺陷 真正理解: 软件测试就是验证软件产品特性是否满足用户的需求 测试定义: 测试人员验证软件是否符合需求的这个过程就是测试 2、为什么要有测试 标准情况下&a…...

VI/VIM的使用
1、vi的基本概念 基本上vi可以分为三种状态,分别是命令模式(command mode)、插入模式(Insert mode)和底行模式(last line mode),各模式的功能区分如下: 1) 命令行模…...

【虹科干货】Redis Enterprise vs ElastiCache——如何选择缓存解决方案?
使用Redis 或 Amazon ElastiCache 来作为缓存加速已经是业界主流的解决方案,二者各有什么优势?又有哪些区别呢? 文况速览: - Redis 是什么? - Redis Enterprise 是什么? - Amazon ElastiCache 是什么&…...
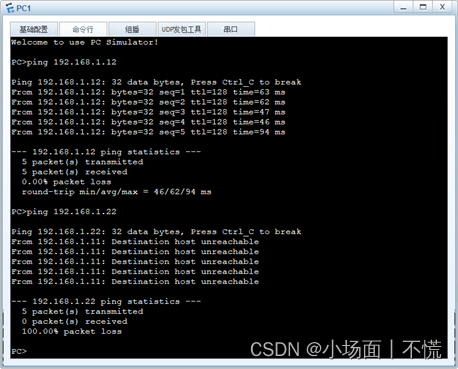
2.2.2 交换机间相同vlan的通信
实验2.2.2 交换机间相同vlan的通信 一、任务描述二、任务分析三、实验拓扑四、具体要求五、任务实施1.设置交换机的名称,创建VLAN,配置access并分配接口。对两台交换机进行相同的VLAN划分,下面是SWA配置过程,同理可实现SWB的配置。…...

C的魅力在于指针
原有的adrv9025 代理框架很好用,在其原有的平台上做改进...

【Linux常用命令14】Linux系统监控常用命令
proc文件系统 /proc/cmdline 加载kernel时的相关指令与参数 /proc/cpuinfo CPU相关信息,包含频率、类型与运算功能 /proc/devices 记录了系统各个主要设备的主设备号码 /proc/filesystems 记录系统加载的文件系统 /proc/loadavg 平均负载值 top看到就是这个 /proc/…...

Python Watchdog:高效的文件系统监控
1. 写在前面 在软件开发中,有时候需要通过 Python 去监听指定区域文件或目录的创建、修改,或者删除,从而引发特定的事件处理。本篇博客为你介绍第三方模块 Watchdog 实现对文件事件的监控。 公众号: 滑翔的纸飞机 2. Watchdog 2…...

C++中多态的原理【精华】
虚函数表 通过一道题我们先感受一下编译器针对多态的处理 #include <iostream> using namespace std;class Base { public:virtual void Func1(){cout << "Func1()" << endl;} private:int _b 1;char _c };int main() {cout << sizeof(B…...

亿赛通电子文档安全管理系统 Update.jsp SQL注入
目录 0x01 漏洞介绍 0x02 影响产品 0x03 语法特征 0x04 漏洞复现页面 0x05 漏洞修复建议 0x01 漏洞介绍 亿赛通电子文档安全管理系统是国内最早基于文件过滤驱动技术的文档加解密产品之一,保护范围涵盖终端电脑(Windows、Mac、Linux系统平台&#…...

神经网络中的反向传播:综合指南
塔曼纳 一、说明 反向传播是人工神经网络 (ANN) 中用于训练深度学习模型的流行算法。它是一种监督学习技术,用于调整网络中神经元的权重,以最小化预测输出和实际输出之间的误差。 在神经网络中,反向传播是计算损失函数…...

协同创新、奔赴未来——“华为云杯”2023人工智能创新应用大赛华丽谢幕
9月27日,在苏州工业园区管理委员会、华为云计算技术有限公司的指导下,由SISPARK(苏州国际科技园)、华为(苏州)人工智能创新中心联合主办,东北大学工业智能与系统优化国家级前沿科学中心、浙江大…...

介绍Node.js中fs模块 代码和注释。
Node.js中的fs模块提供了一些用于文件系统操作的API,包括文件读写、目录操作等。 读取文件 使用fs.readFile()方法可以读取文件内容。该方法的第一个参数是文件路径,第二个参数是可选的选项对象,第三个参数是回调函数。回调函数的第一个参数…...

【QT 读取JSON】 深入浅出 使用QT内置的QJson模块解析Json文件 匠心之作
目录 0 引言1 Json数据分析2 解析Json数据 🙋♂️ 作者:海码007📜 专栏:QT专栏💥 标题:【QT 读取JSON】 使用QT内置的QJson模块解析Json文件❣️ 寄语:人生的意义或许可以发挥自己全部的潜力&…...

初识javaweb2 tomcat
如果是tomcat启动成功却无法通过localhost:8080进入页面,先去查看是否是端口号被占用, 再用命令中断占用的进程,如果简单的命令窗口无法中断,切换到管理员身份运行即可 netstat -ano|findstr "8080" 查看那个进程占用了…...

使用OPENROWSET :在一个数据库中查询另一个数据库的数据
当你需要在一个数据库中查询另一个数据库的数据时,SQL Server提供了多种方法来实现这一目标。一种常见的方法是使用链接服务器(Linked Server),另一种方法是使用 OPENROWSET 函数。本篇博客将重点介绍如何使用 OPENROWSET 函数在当…...
)
基于STM32设计的智慧农业管理系统(ESP8266+腾讯云微信小程序)
一、项目介绍 基于STM32设计的智慧农业控制系统(ESP8266+腾讯云微信小程序) 1.1 项目背景 随着人们对食品安全和生态环境的日益重视,智慧农业逐渐成为一个备受关注的领域。智能化管理可以提高农业生产效率,减少资源浪费,改善生态环境。因此,基于物联网技术的智慧农业管理系…...
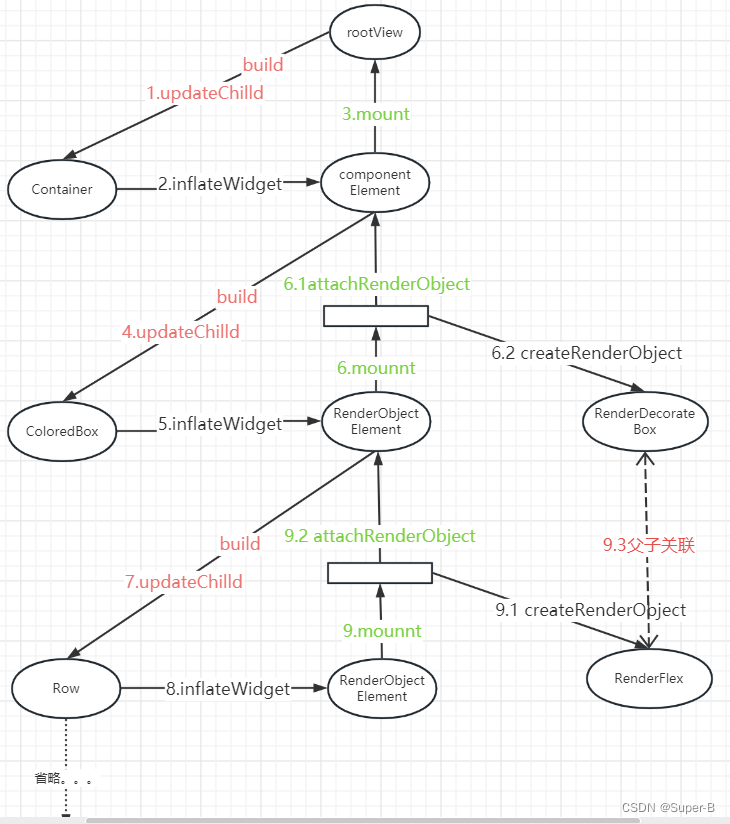
Flutter视图原理之三棵树的建立过程
目录 三棵树的关系树的构建过程1.updateChild函数(element的复用)2.inflateWidget函数3.mount函数3.1 componentElement的实现3.2 RenderObjectElement的实现3.2.1 attachRenderObject函数 4.performRebuild函数 总结三棵树创建流程 三棵树的关系 Flutt…...

详细解析冒泡排序,JS如何基本实现的。
目录 冒泡排序是什么: 使用冒泡排序是为了什么: DEMO示例: 冒泡排序是什么: 冒泡排序(Bubble Sort)是一种简单的比较排序算法,它通过多次遍历待排序的元素,比较相邻元素的大小,如果它们的顺序不正确就交换它们&…...

如何消除CSDN博文代码中自动添加的行号
哪里有自定义目录标题 编写CSDN博文,使用代码块的linux命令行,预览时没有代码行号,但发布文章后自动添加了行号。 git clone https://github.com/mikel-brostrom/yolo_tracking.git cd yolo_tracking pip install -v -e .为什么预览和发布的…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
