线性代数-Python-01:向量的基本运算 -手写Vector -学习numpy的基本用法
文章目录
- 代码
- 目录结构
- Vector.py
- _globals.py
- main_vector.py
- main_numpy_vector.py
- 一、创建属于自己的向量
- 1.1 在控制台测试__repr__和__str__方法
- 1.2 创建实例测试代码
- 二、向量的基本运算
- 2.1 加法
- 2.2 数量乘法
- 2.3 向量运算的基本性质
- 2.4 零向量
- 2.5 向量的长度
- 2.6 单位向量
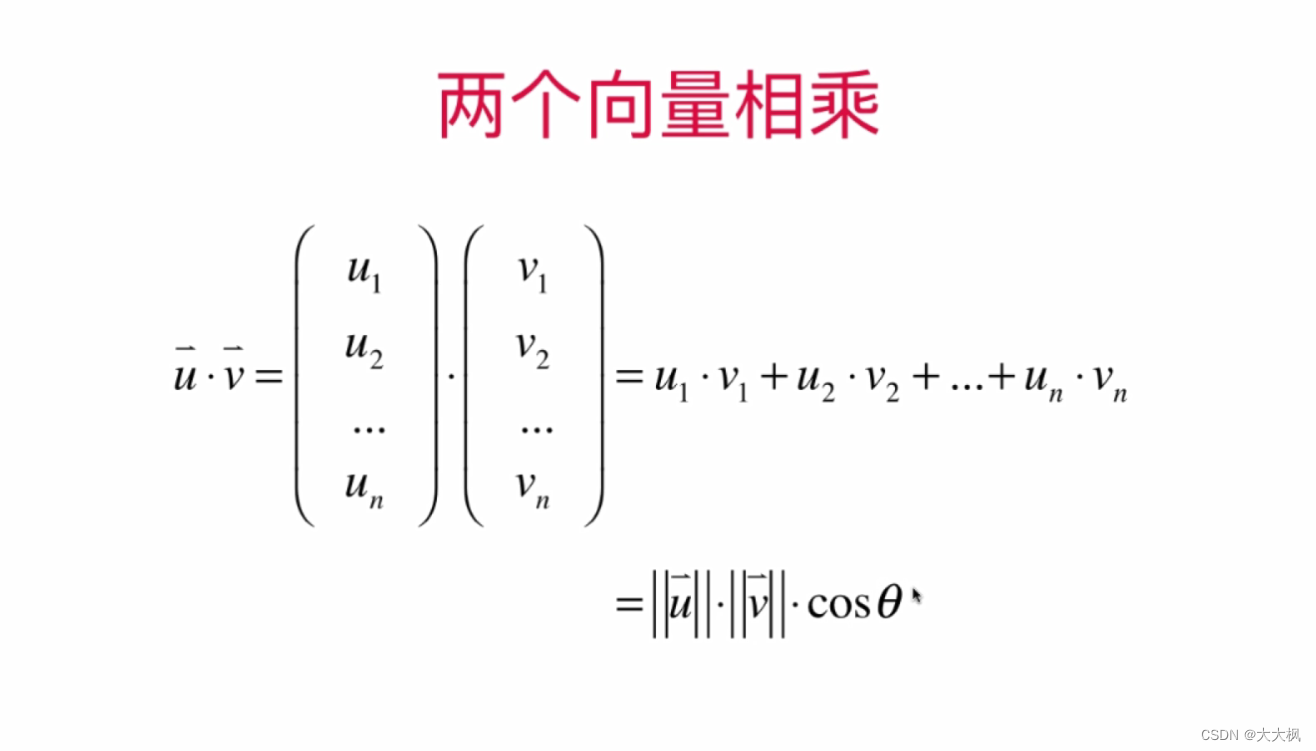
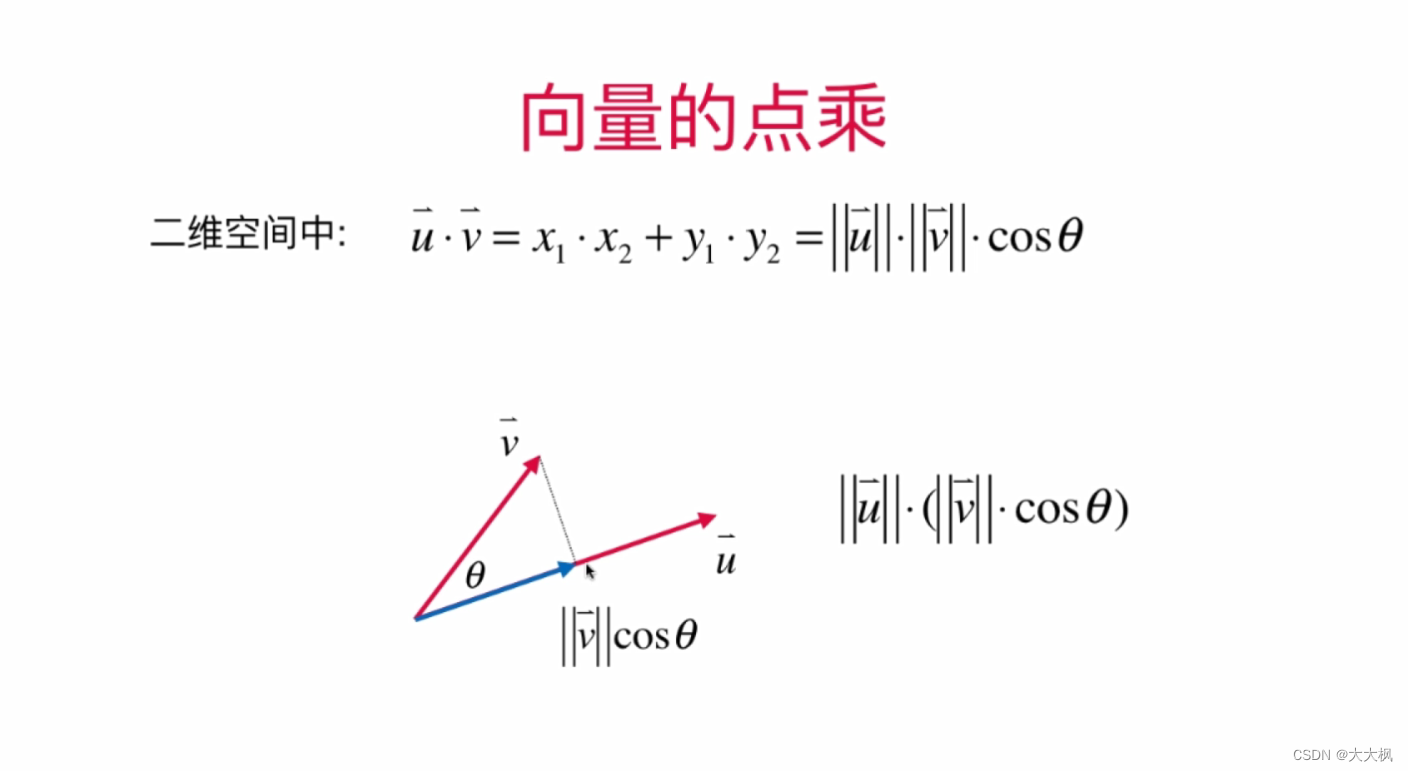
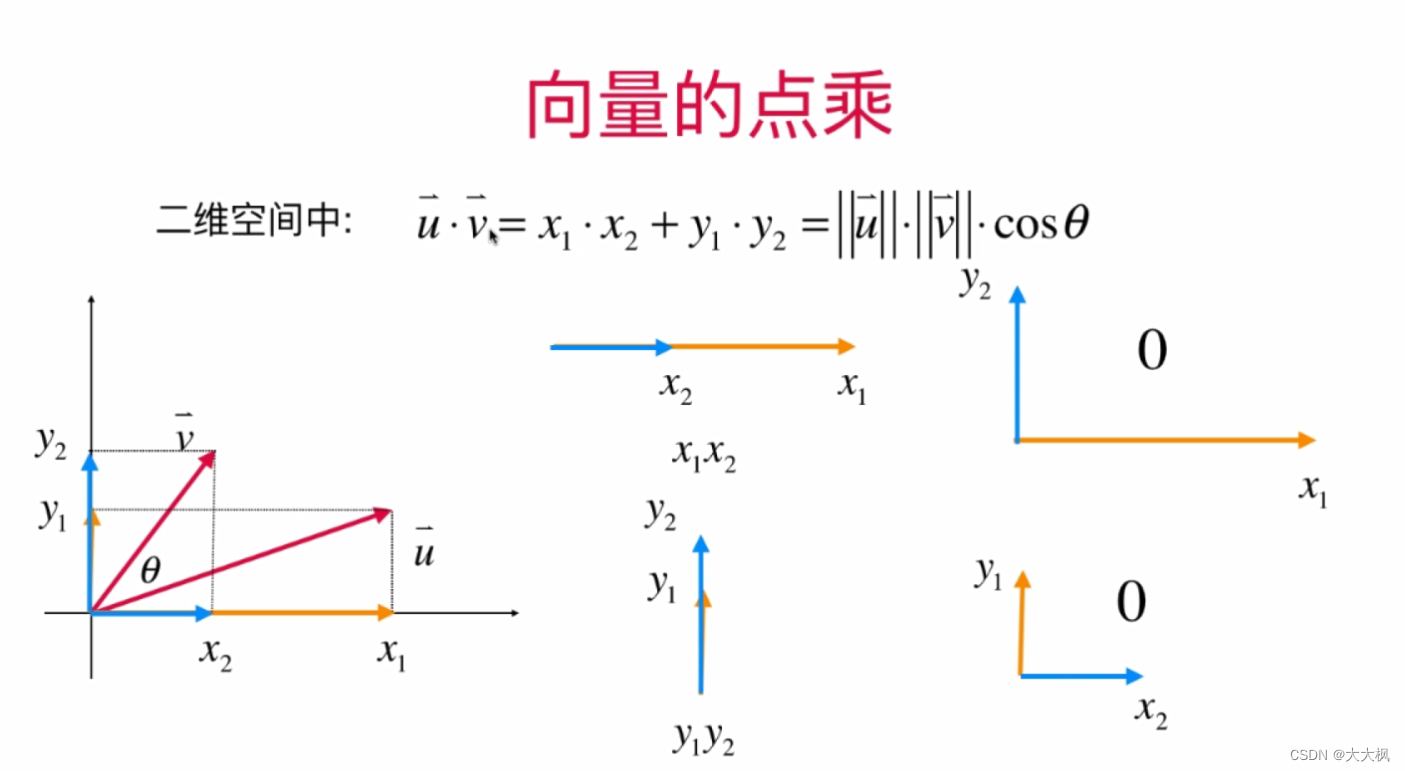
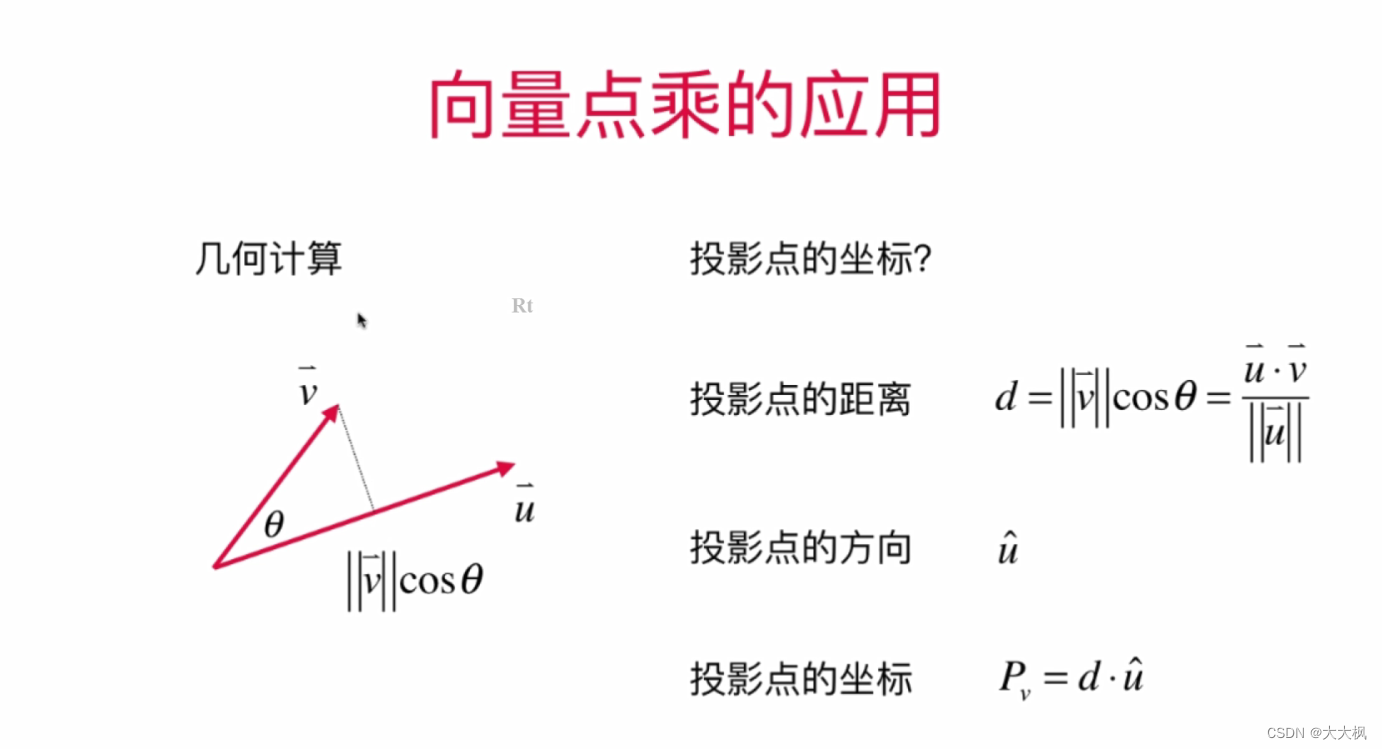
- 2.7 点乘/内积:两个向量的乘法 --答案是一个标量
代码
目录结构
F:.
| main_numpy_vector.py
| main_vector.py
|
+---.idea
|
\---playLA| Vector.py| _globals.py| __init__.py|\---__pycache__
Vector.py
import math
from ._globals import EPSILON
class Vector:def __init__(self, lst):"""__init__ 代表类的构造函数双下划线开头的变量 例如_values,代表类的私有成员lst是个引用,list(lst)将值复制一遍,防止用户修改值"""self._values = list(lst)def dot(self, another):"""向量点乘,返回结果标量"""assert len(self) == len(another), \"Error in dot product. Length of vectors must be same."return sum(a * b for a, b in zip(self, another))def norm(self):"""返回向量的模"""return math.sqrt(sum(e**2 for e in self))def normalize(self):"""归一化,规范化返回向量的单位向量此处设计到了除法: def __truediv__(self, k):"""if self.norm() < EPSILON:raise ZeroDivisionError("Normalize error! norm is zero.")return Vector(self._values) / self.norm()# return 1 / self.norm() * Vector(self._values)# return Vector([e / self.norm() for e in self])def __truediv__(self, k):"""返回数量除法的结果向量:self / k"""return (1 / k) * self@classmethoddef zero(cls, dim):"""返回一个dim维的零向量@classmethod 修饰符对应的函数不需要实例化,不需要 self 参数,但第一个参数需要是表示自身类的cls参数,可以来调用类的属性,类的方法,实例化对象等。"""return cls([0] * dim)def __add__(self, another):"""向量加法,返回结果向量"""assert len(self) == len(another), \"Error in adding. Length of vectors must be same."# return Vector([a + b for a, b in zip(self._values, another._values)])return Vector([a + b for a, b in zip(self, another)])def __sub__(self, another):"""向量减法,返回结果向量"""assert len(self) == len(another), \"Error in subtracting. Length of vectors must be same."return Vector([a - b for a, b in zip(self, another)])def __mul__(self, k):"""返回数量乘法的结果向量:self * k"""return Vector([k * e for e in self])def __rmul__(self, k):"""返回数量乘法的结果向量:k * selfself本身就是一个列表"""return self * kdef __pos__(self):"""返回向量取正的结果向量"""return 1 * selfdef __neg__(self):"""返回向量取负的结果向量"""return -1 * selfdef __iter__(self):"""返回向量的迭代器"""return self._values.__iter__()def __getitem__(self, index):"""取向量的第index个元素"""return self._values[index]def __len__(self):"""返回向量长度(有多少个元素)"""return len(self._values)def __repr__(self):"""打印显示:Vector([5, 2])"""return "Vector({})".format(self._values)def __str__(self):"""打印显示:(5, 2)"""return "({})".format(", ".join(str(e) for e in self._values))
_globals.py
# 包中的变量,但是对包外不可见,因此使用“_”开头
EPSILON = 1e-8
main_vector.py
from playLA.Vector import Vectorif __name__ == "__main__":vec = Vector([5, 2])print(vec)print("len(vec) = {}".format(len(vec)))print("vec[0] = {}, vec[1] = {}".format(vec[0], vec[1]))vec2 = Vector([3, 1])print("{} + {} = {}".format(vec, vec2, vec + vec2))print("{} - {} = {}".format(vec, vec2, vec - vec2))print("{} * {} = {}".format(vec, 3, vec * 3))print("{} * {} = {}".format(3, vec, 3 * vec))print("+{} = {}".format(vec, +vec))print("-{} = {}".format(vec, -vec))zero2 = Vector.zero(2)print(zero2)print("{} + {} = {}".format(vec, zero2, vec + zero2))print("norm({}) = {}".format(vec, vec.norm()))print("norm({}) = {}".format(vec2, vec2.norm()))print("norm({}) = {}".format(zero2, zero2.norm()))print("normalize {} is {}".format(vec, vec.normalize()))print(vec.normalize().norm())print("normalize {} is {}".format(vec2, vec2.normalize()))print(vec2.normalize().norm())try:zero2.normalize()except ZeroDivisionError:print("Cannot normalize zero vector {}.".format(zero2))print("========点乘:========")print(vec.dot(vec2))main_numpy_vector.py
import numpy as npif __name__ == "__main__":print(np.__version__)# np.array 基础print("========np.array 基础========")lst = [1, 2, 3]lst[0] = "Linear Algebra"print(lst)print("========vec = np.array([1, 2, 3])========")vec = np.array([1, 2, 3])print(vec)# vec[0] = "Linear Algebra"# vec[0] = 666# print(vec)print("========np.array的创建========")# np.array的创建print(np.zeros(5))print(np.ones(5))print(np.full(5, 666))print("========np.array的基本属性========")# np.array的基本属性print(vec)print("size =", vec.size)print("size =", len(vec))print(vec[0])print(vec[-1])print(vec[0: 2])print(type(vec[0: 2]))print("========np.array的基本运算========")# np.array的基本运算vec2 = np.array([4, 5, 6])print("{} + {} = {}".format(vec, vec2, vec + vec2))print("{} - {} = {}".format(vec, vec2, vec - vec2))print("{} * {} = {}".format(2, vec, 2 * vec))print("没有数学意义的乘法:{} * {} = {}".format(vec, vec2, vec * vec2))print("{}.dot({}) = {}".format(vec, vec2, vec.dot(vec2)))print("========求模========")print(np.linalg.norm(vec))print("========归一化========")print(vec / np.linalg.norm(vec))print("========单位向量========")print(np.linalg.norm(vec / np.linalg.norm(vec)))print("========零向量会报错========")zero3 = np.zeros(3)print(zero3 / np.linalg.norm(zero3))一、创建属于自己的向量
class Vector:def __init__(self, lst):self._values = lstdef __getitem__(self, index):"""取向量的第index个元素"""return self._values[index]def __len__(self):"""返回向量长度(有多少个元素)"""return len(self._values)def __repr__(self):"""打印显示:Vector([5, 2])"""return "Vector({})".format(self._values)def __str__(self):"""打印显示:(5, 2)"""return "({})".format(", ".join(str(e) for e in self._values))
1.1 在控制台测试__repr__和__str__方法
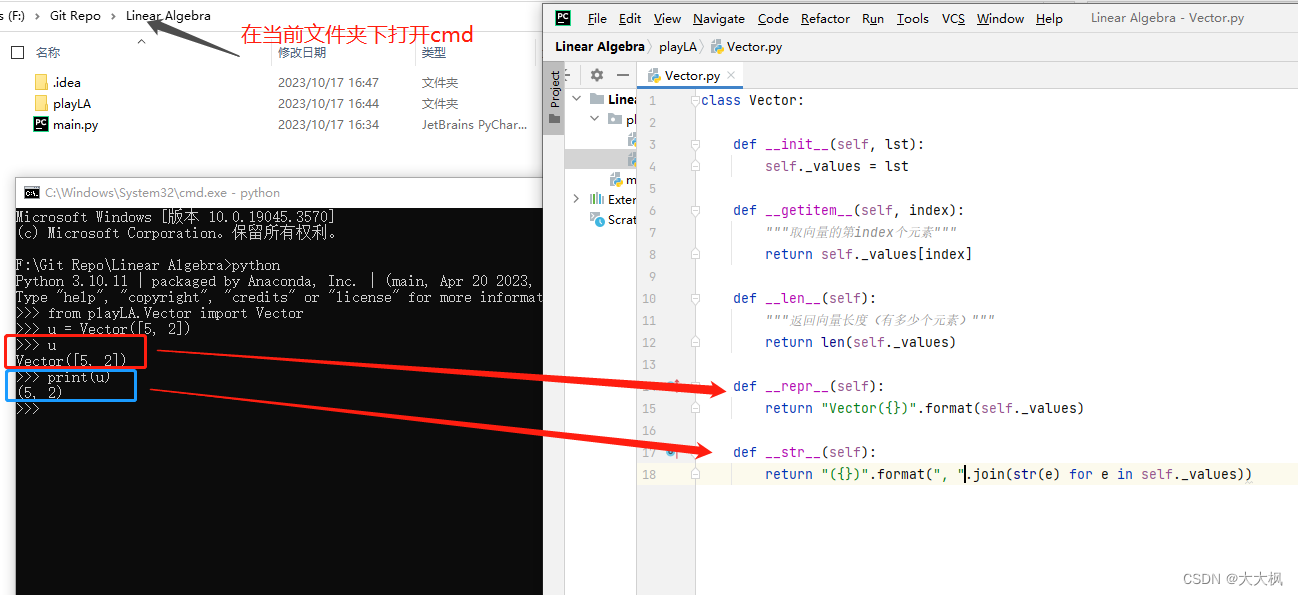
1.2 创建实例测试代码
from playLA.Vector import Vectorif __name__ == "__main__":vec = Vector([5, 2])print(vec)print("len(vec) = {}".format(len(vec)))print("vec[0] = {}, vec[1] = {}".format(vec[0], vec[1]))
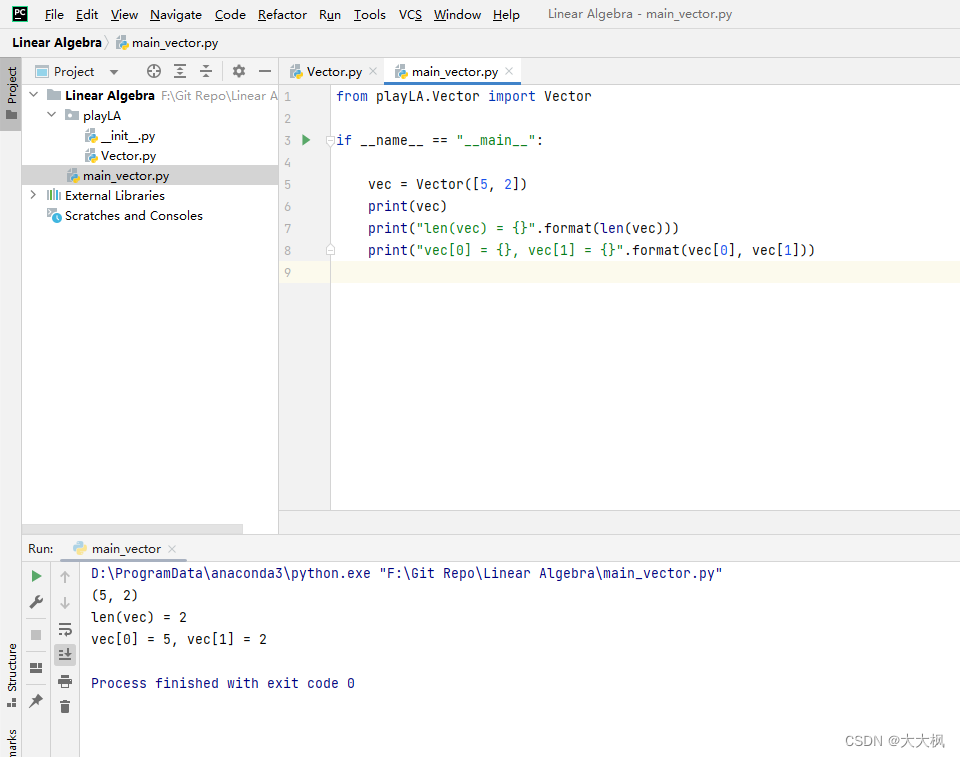
二、向量的基本运算
2.1 加法

2.2 数量乘法

2.3 向量运算的基本性质

2.4 零向量




2.5 向量的长度


2.6 单位向量
单位向量叫做 u hat
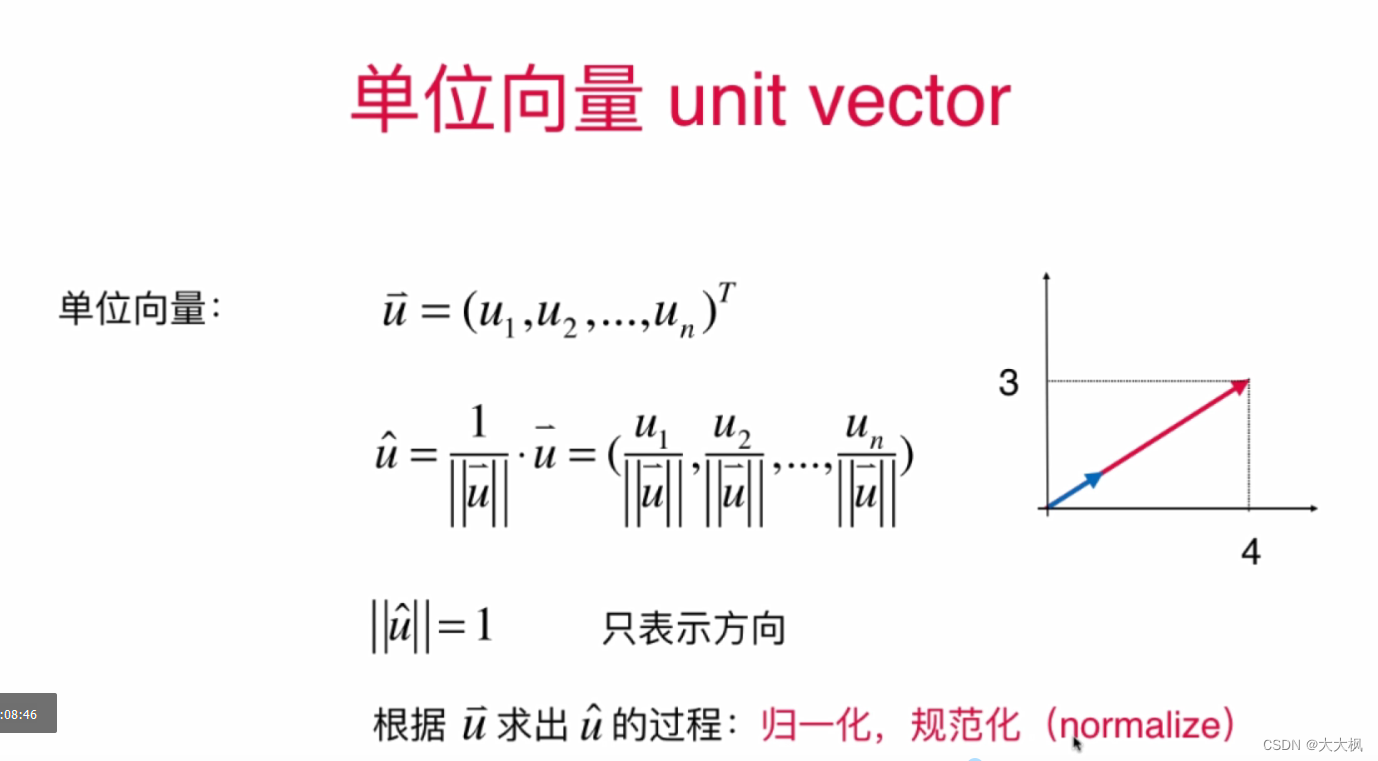

2.7 点乘/内积:两个向量的乘法 --答案是一个标量





相关文章:

线性代数-Python-01:向量的基本运算 -手写Vector -学习numpy的基本用法
文章目录 代码目录结构Vector.py_globals.pymain_vector.pymain_numpy_vector.py 一、创建属于自己的向量1.1 在控制台测试__repr__和__str__方法1.2 创建实例测试代码 二、向量的基本运算2.1 加法2.2 数量乘法2.3 向量运算的基本性质2.4 零向量2.5 向量的长度2.6 单位向量2.7 …...
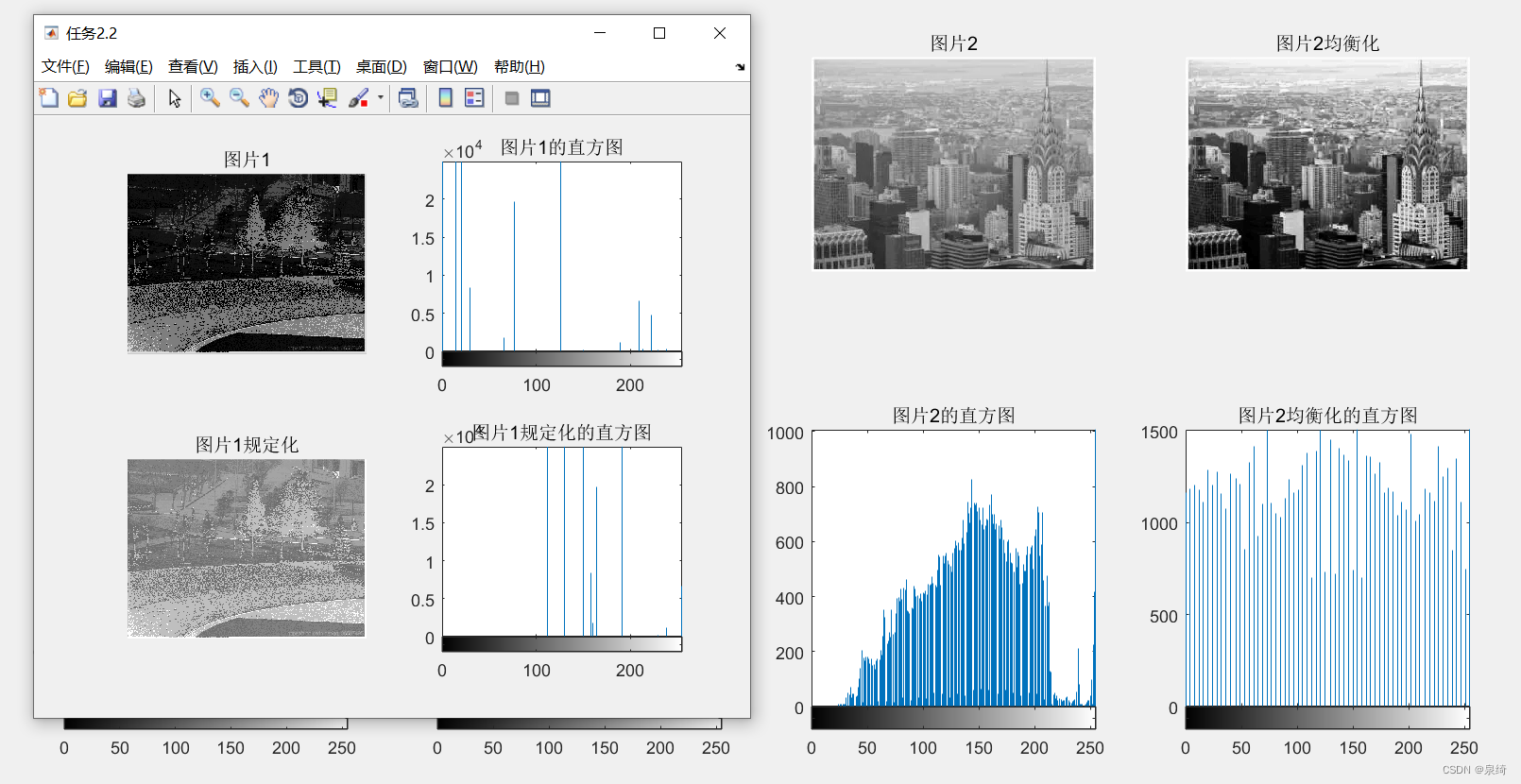
数字图像处理实验记录二(直方图和直方图均衡化)
文章目录 一、基础知识1,什么是直方图2,直方图有什么用3,直方图均衡化4、原理代码实现 二、实验要求任务1:任务2: 三、实验记录任务1:任务2: 四、结果展示任务1:任务2: 五…...

大数据Flink(九十九):SQL 函数的解析顺序和系统内置函数
文章目录 SQL 函数的解析顺序和系统内置函数 一、SQL 函数...
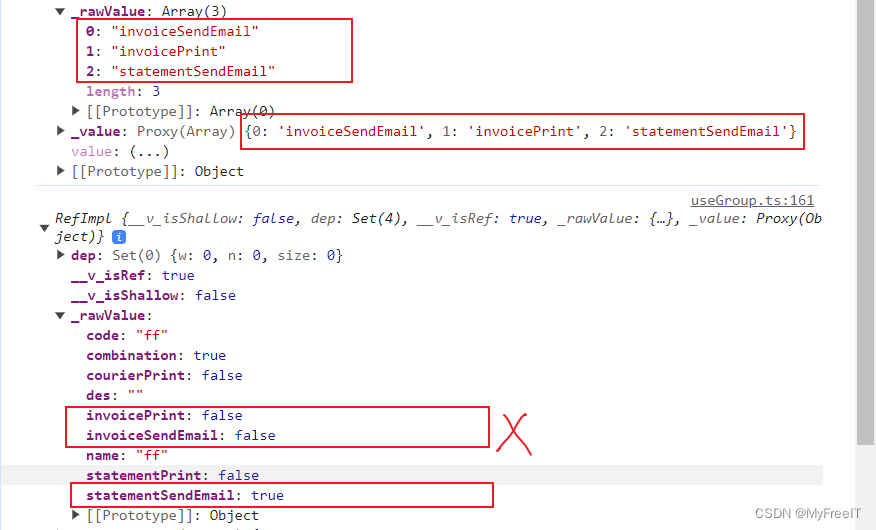
TODO Vue typescript forEach的bug,需要再核實
forEach 一個string[],只有最後一個匹配條件有效,其它條件無效。 所以,只能替換成普通的for循環。 console.log(taskList)// for (const _task of taskList.value) {// if (_task invoiceSendEmail) {// form.value.invoiceSendEmail…...

简记一个错误
简记一个Flutter错误: Using hardware rendering with device sdk gphone64 x86 64. If you notice graphics artifacts, consider enabling software rendering with “–enable-software-rendering”. Launching lib\main.dart on sdk gphone64 x86 64 in debug …...

第四次作业
1.打印各种图形 A.矩形 a int(input("请输入行数: ")) i 0 while i < a:print("*"*10)i1 结果: B.直角三角形 a int(input("请输入行数: ")) i 0 while i<a:print("*"*(i1))i1 结果: C.反直角三角形 …...

面试问题整理总结
1.自我介绍 2.为什么想转测试 想换一个方向,测试开发在一定程度上也是属于开发,而且站在测试的角度能看到全局的东西更多,对需求的理解需要更深”,之前的开发工作比较专一,测试的视野更加开阔,想要站在更高…...

进阶JAVA篇- Collection 类的常用的API与 Collection 集合的遍历方式
目录 1.0 Collection 类的说明 1.1 Collection 类中的实例方法 2.0 Collection 集合的遍历方式(重点) 2.1 使用迭代器( Iterator )进行遍历 2.2 使用增强型 for 循环进行遍历 2.3 使用 Java 8的 Stream API 进行遍历(使…...
CentOS | 添加普通用户并授权sudo
sudo -i adduser peter passwd peter whereis sudoers nano /etc/sudoers添加一行新用户到root组 ## Allow root to run any commands anywhere root ALL(ALL) ALL peter ALL(ALL) ALL如果提升权限后无法cd到其他目录等,修改 /etc/passwd 文件&…...
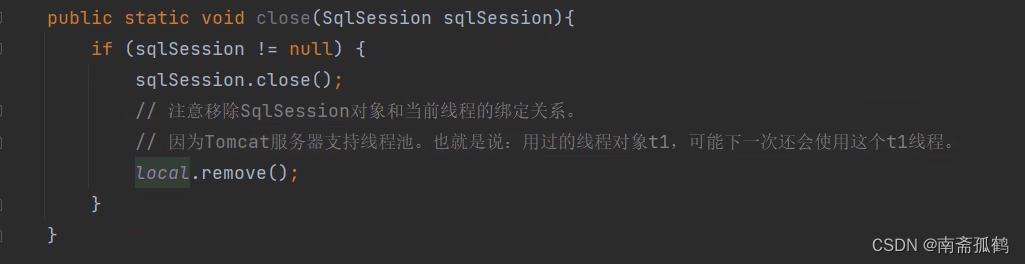
【MyBatis】mybatis工具类迭代
目录 MyBatis工具类的迭代 ThreadLocal使用 mybatis工具类终极版: MyBatis工具类的迭代 public class MyBatisUtil {//工具类构造方法私有化private void MyBatisUtil() {}//方法一public static SqlSession getSqlSession(){try {SqlSessionFactoryBuilder sql…...
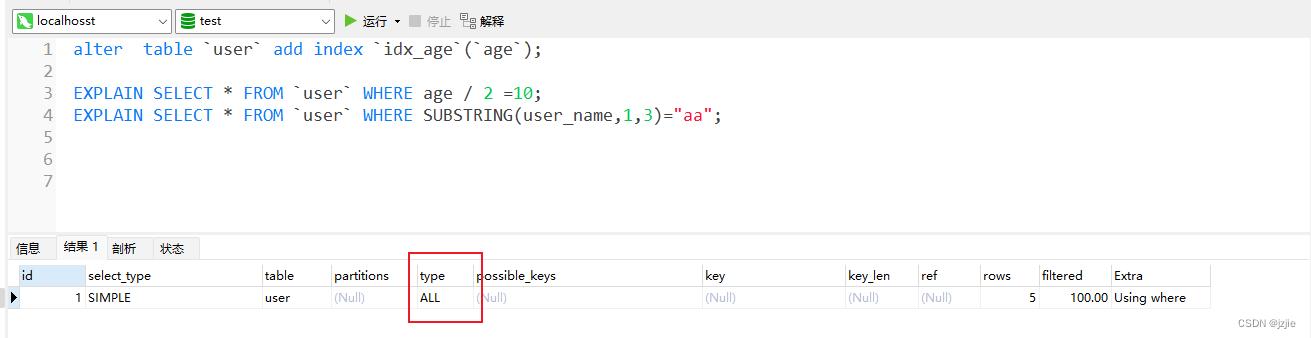
MSQL系列(六) Mysql实战-SQL语句优化
Mysql实战-SQL语句优化 前面我们讲解了索引的存储结构,BTree的索引结构,以及索引最左侧匹配原则,Explain的用法,可以看到是否使用了索引,今天我们讲解一下SQL语句的优化及如何优化 文章目录 Mysql实战-SQL语句优化1.…...

kaggle新赛:UBC卵巢癌亚型分类和异常检测大赛【图像分类】
赛题名称:UBC Ovarian Cancer Subtype Classification and Outlier Detection (UBC-OCEAN) 赛题链接:https://www.kaggle.com/competitions/UBC-OCEAN 赛题背景 卵巢癌是女性生殖系统最致命的癌症。目前,卵巢癌诊断依赖病理学家评估亚型。…...

基于nodejs+vue云旅青城系统
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

《孙哥说Spring5》笔记汇总
时隔两个多月,终于将《孙哥说Spring5》的笔记文章全部整理完了,在这里做个汇总。孙哥的Spring课讲的非常好,深度和广度都有所兼顾,推荐大家去看 点击学习《孙哥说Spring5》 基础铺垫 1️⃣ Spring5应用之基础扫盲2️⃣ Spring5应…...

在使用了spring-cloud-starter-gateway后,为什么还会发生cors问题
//1.需要配置类 import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.web.cors.CorsConfiguration; import org.springframework.web.cors.reactive.CorsWebFilter; import org.sp…...
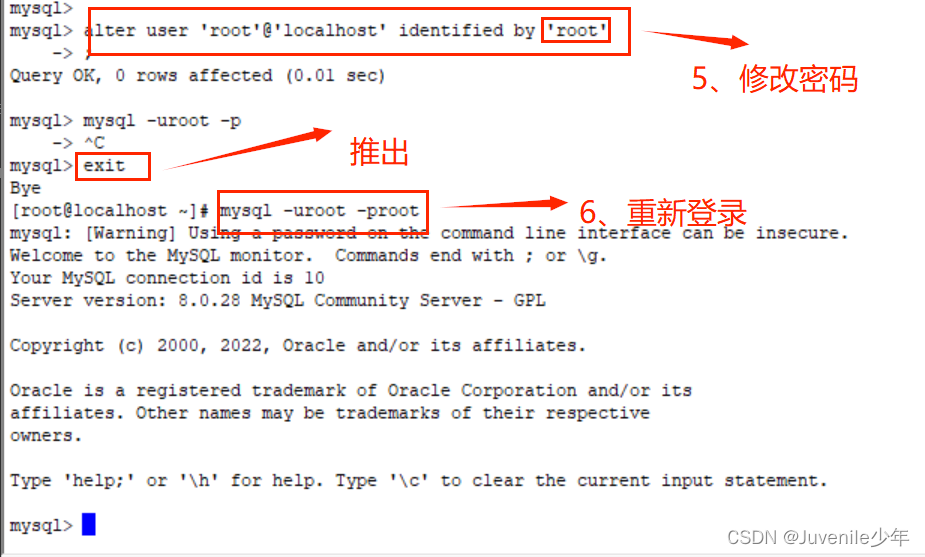
CentOS7安装MySQL8.0.28
CentOS7安装MySQL8.0.28 一、下载MySQL安装包二、安装配置mysql 一、下载MySQL安装包 点击以下链接可以自动跳转:MySQL官网 接下来按如图所示依次点击进入。 选择自己所需要版本 此处如需下载历史版本可以点击 二、安装配置mysql 1、登录ssh或其他相关软件上…...
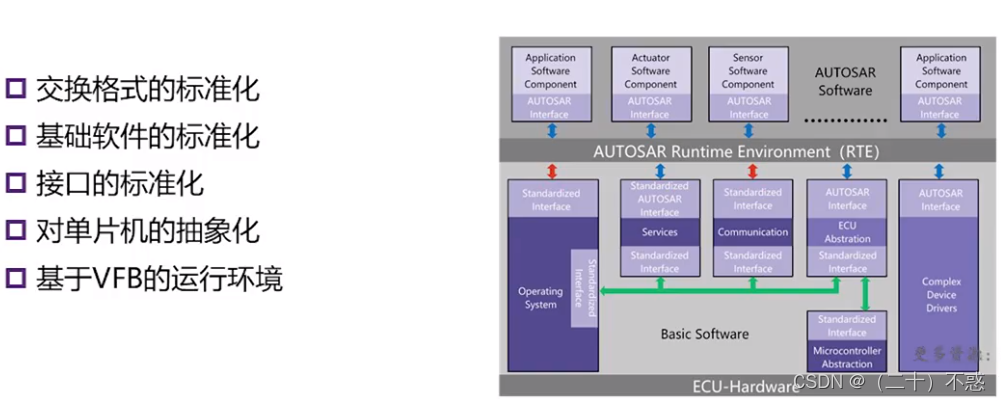
AutoSAR入门:应用背景及简介
1、应用背景 在我们现在的汽车行业里面,汽车电子的发展过程中,我们发现有一些新的趋势汽车电子系统的复杂性不断增长。 我们现在可以看到车辆有越来越多的功能,那么这些功能呢,也在往这个控制器上进行集中,比如说我们现…...
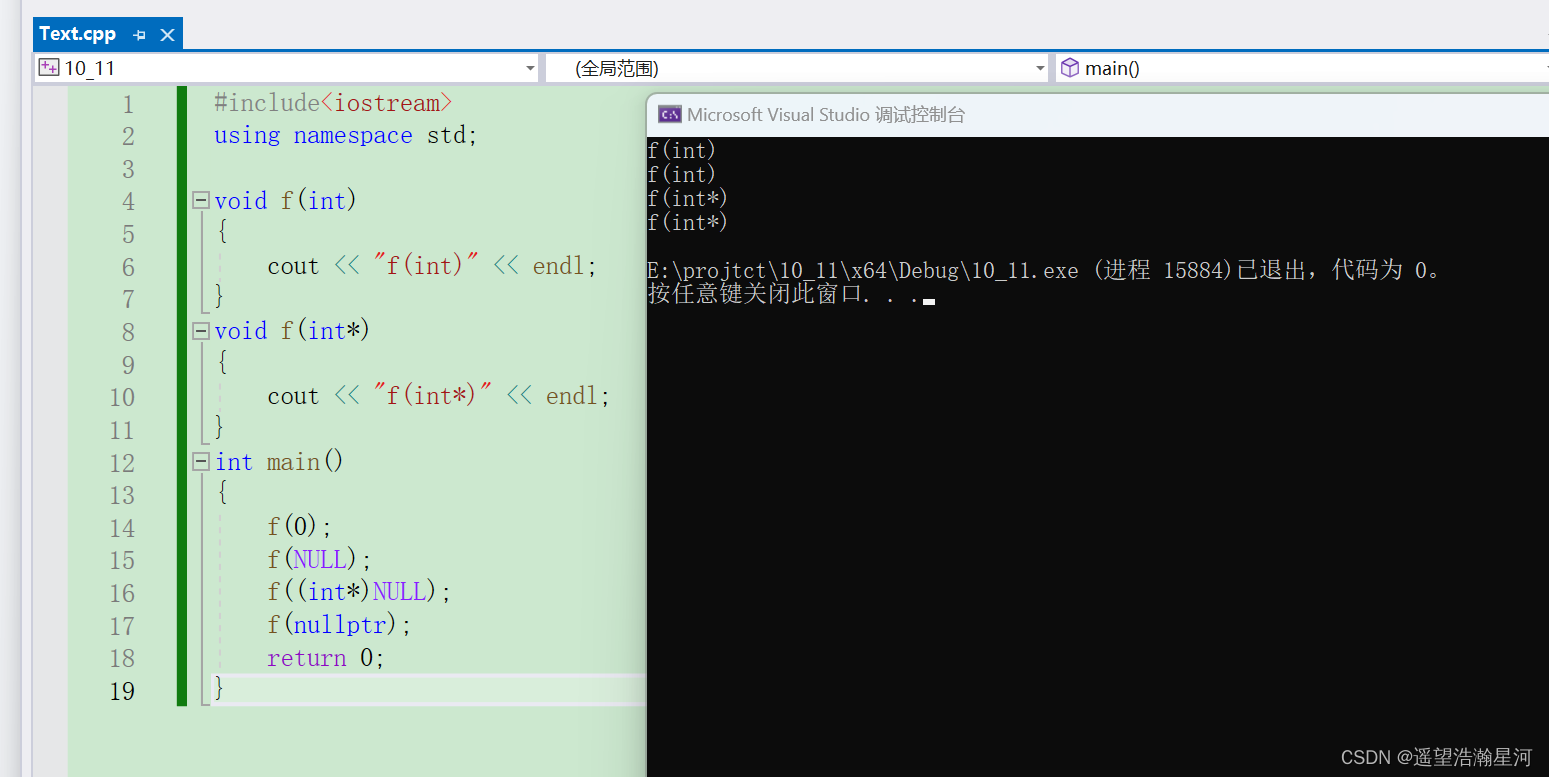
C++初阶(三)
文章目录 一、auto关键字(C11)1、auto简介2、auto使用规则1、 auto与指针和引用结合起来使用2、 在同一行定义多个变量 3、auto不能推导的场景1、 auto不能作为函数的参数2、 auto不能直接用来声明数组3、特性总结 二、基于范围的for循环(C11)1、范围for的语法2、 范围for的使用…...
PHP的学习入门建议
学习入门PHP的步骤如下: 确定学习PHP的目的和需求,例如是为了开发网站还是为了与数据库交互等。学习PHP的基础语法和程序结构,包括变量、数据类型、循环、条件等。学习PHP的面向对象编程(OOP)概念和技术。学习与MySQL…...

骰子涂色(Cube painting, UVa 253)rust解法
输入两个骰子,判断二者是否等价。每个骰子用6个字母表示,如图4-7所示。 例如rbgggr和rggbgr分别表示如图4-8所示的两个骰子。二者是等价的,因为图4-8(a)所示的骰子沿着竖直轴旋转90之后就可以得到图4-8(b&a…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
