机器学习-最小二乘法
概况
最小二乘法其实就是为数据(二维)拟合出一条直线,为(三维)数据拟合出一个面。来最大程度的是我们的样本点落在该直线上。
使得我们找到一条直线使所以的样本点尽可能靠近该直线,即每个样本点到直线的距离最短。
Y=WX+B,W是权重,B是偏移量。
损失函数
L ( w ) = ∑ i = 1 m ∣ ∣ w T x i − y i ∣ ∣ 2 L(w)=\sum_{i=1}^m||w^Tx_i-y_i||^2 L(w)=i=1∑m∣∣wTxi−yi∣∣2
= ∑ i = 1 m ( w T x i − y i ) 2 =\sum_{i=1}^m(w^Tx_i-y_i)^2 =i=1∑m(wTxi−yi)2
= [ W T X T − Y t ] [ X W − Y ] =[W^TX^T-Y^t][XW-Y] =[WTXT−Yt][XW−Y]
= W T X T X W − Y T X W − W T X T Y + Y T Y =W^TX^TXW-Y^TXW-W^TX^TY+Y^TY =WTXTXW−YTXW−WTXTY+YTY
= W T X T X W − 2 W T X T Y + Y T Y =W^TX^TXW-2W^TX^TY+Y^TY =WTXTXW−2WTXTY+YTY
为什么 Y T X W Y^TXW YTXW和 W T X T Y W^TX^TY WTXTY是相等的,因为 Y T Y^T YT的维度是(1,n), X X X的维度是(n,n), W W W的维度是(n,1),所以 Y T X W Y^TXW YTXW的维度是(1,1)也就是一个常数值。而 W T W^T WT的维度为(1,n), X T X^T XT的维度为(n,n), Y Y Y的维度为(n,1)。 W T X T Y W^TX^TY WTXTY的维度为(1,1)所以都是常数,所以转置不转置不影响数值的值。所以是相等的。
因为我们采用的是最小二乘估计,所以这里希望损失函数最小,所以求取函数导数为0的点,就是我们的最优解,因为这里是二次函数,所以导数为0的点就是最值点。
最优解为 w ∗ w^* w∗
w ∗ = a r g m i n w L ( w ) w^*=argmin_wL(w) w∗=argminwL(w)
对其求导,并令其导数为0.
导数 = 2 X T X W − 2 X T Y = 0 导数=2X^TXW-2X^TY=0 导数=2XTXW−2XTY=0
具体过程是:
d L ( w ) = d ( W T X T X W − 2 W T X T Y + Y T Y ) dL(w)=d(W^TX^TXW-2W^TX^TY+Y^TY) dL(w)=d(WTXTXW−2WTXTY+YTY)
= d ( W T ) X T X W − 2 d ( W T ) X T Y + W T X T X d ( W ) =d(W^T)X^TXW-2d(W^T)X^TY+W^TX^TXd(W) =d(WT)XTXW−2d(WT)XTY+WTXTXd(W)
= X T X W d ( W ) − 2 X T Y d ( W ) + W T X T X d ( W ) =X^TXWd(W)-2X^TYd(W)+W^TX^TXd(W) =XTXWd(W)−2XTYd(W)+WTXTXd(W)
即 2 X T X W − 2 X T Y = 0 2X^TXW-2X^TY=0 2XTXW−2XTY=0
w ∗ = ( X T X ) − 1 X T Y w^*=(X^TX)^{-1}X^TY w∗=(XTX)−1XTY
然后我们可以构造决策函数:
f ( x ) = ( w ∗ ) T x f(x)=(w^*)^Tx f(x)=(w∗)Tx
相关文章:

机器学习-最小二乘法
概况 最小二乘法其实就是为数据(二维)拟合出一条直线,为(三维)数据拟合出一个面。来最大程度的是我们的样本点落在该直线上。 使得我们找到一条直线使所以的样本点尽可能靠近该直线,即每个样本点到直线的距离最短。 YWXB,W是权重࿰…...
Linux文件管理与用户管理
一、查看文件内容 1、回顾之前的命令 cat命令、tac命令、head命令、tail命令、扩展:tail -f动态查看一个文件的内容 2、more分屏显示文件内容(了解) 基本语法: # more 文件名称 特别注意:more命令在加载文件时并不…...

java中什么是不可变类
什么是不可变类 不可变类是指一旦创建对象后,其状态(属性值)就不能被修改的类。 一个不可变类具有以下特征: 类的实例变量声明为私有的,并且没有提供修改这些变量值的公共方法。类是final的,防止被继承。类的实例变量声明为fin…...

使用Perl和WWW::Mechanize库编写
以下是一个使用Perl和WWW::Mechanize库编写的网络爬虫程序的内容。代码必须使用以下代码:jshk.com.cn/get_proxy 首先,确保已经安装了Perl和WWW::Mechanize库。如果没有,请使用以下命令安装: cpan WWW::Mechanize创建一个新的Pe…...

智荟雄安,创想未来 | 竹云董事长受邀出席雄安新区2023软件和信息技术服务业创新发展论坛并作主题演讲
10月18日,以“智荟雄安 创想未来”为主题的雄安新区2023软件和信息技术服务业创新发展论坛在雄安新区国际酒店会议中心召开。河北省委常委,雄安新区党工委书记、管委会主任张国华出席活动。 中国科学院院士朱鲁华现场致辞,中国工程院院士邬贺…...
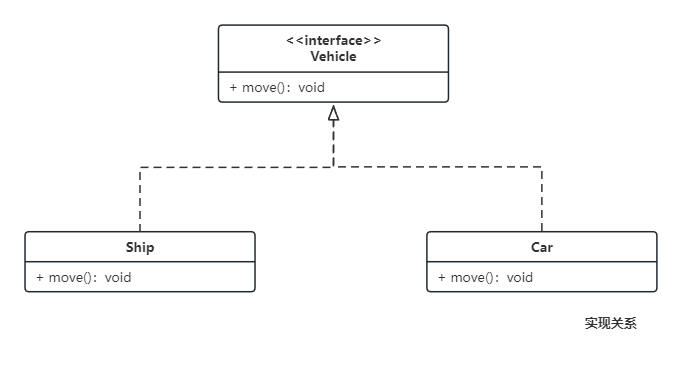
【设计模式-1】UML和设计原则
说明:设计模式(Design Pattern)对于软件开发,简单来说,就是软件开发的套路,固定模板。在学习设计模式之前,需要首先学习UML(Unified Modeling Language,统一建模语言&…...
【数据结构】——二叉树的基础知识
数概念及结构 数的分类 二叉树、多叉树 数的概念 树是一种非线性的数据结构,它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做树的原因是它看起来像一颗倒挂的树,也就是说它是跟朝上,而叶朝下的。 有一个特殊的节点&…...

日常bug汇总
1.constraintlayout NestedScrollView 可能会导致NestedScrollView 不滑动 2.截屏 open class SecureFragment : LogLifecycleFragment() {override fun onResume() {super.onResume()if (!BuildConfig.DEV) {requireActivity().window.setFlags(WindowManager.LayoutParam…...
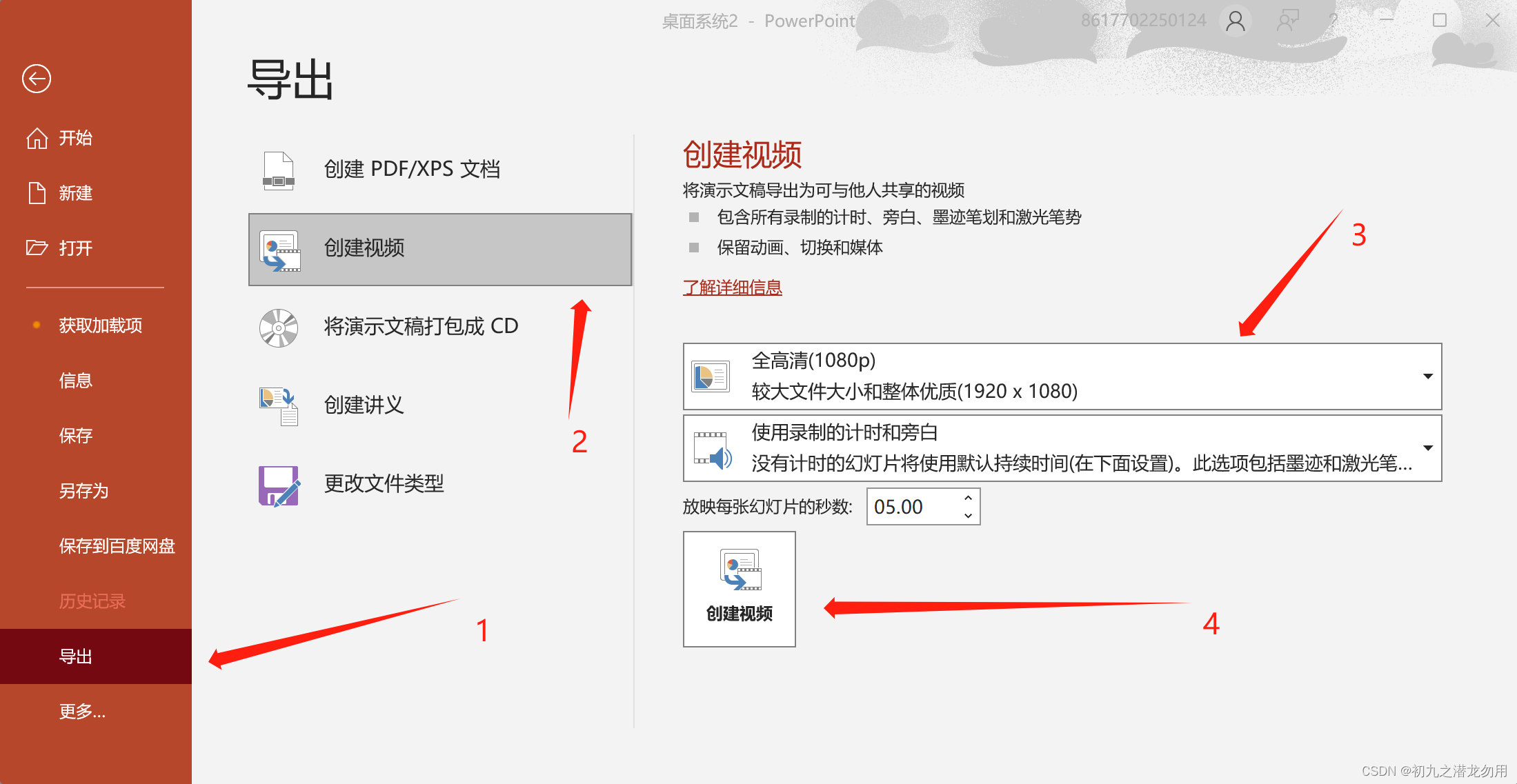
C#使用PPT组件的CreateVideo方法生成视频
目录 需求 实现 CreateVideo方法 关键代码 CreateVideoStatus 其它 需求 我们在使用PowerPoint文档时,经常会使用其导出功能以创建视频,如下图: 手工操作下,在制作好PPT文件后,点击文件 -> 导出 -> 创建视…...
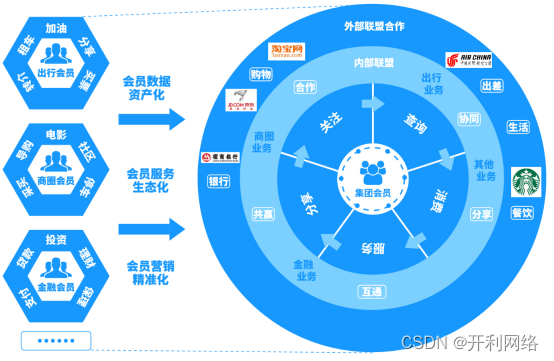
数字化体系如何帮助企业拓展裂变增长渠道?数字化营销体系构建?
在当前的商业环境中,数字不仅仅是数据,还代表着技术和资产。企业数字化正是将数据转化为资产的过程。从信息化时代到数字化时代,企业逐渐将业务和组织、管理和创收都朝着在线化和数据化的方向发展,特别是企业的业务板块。数字化营…...
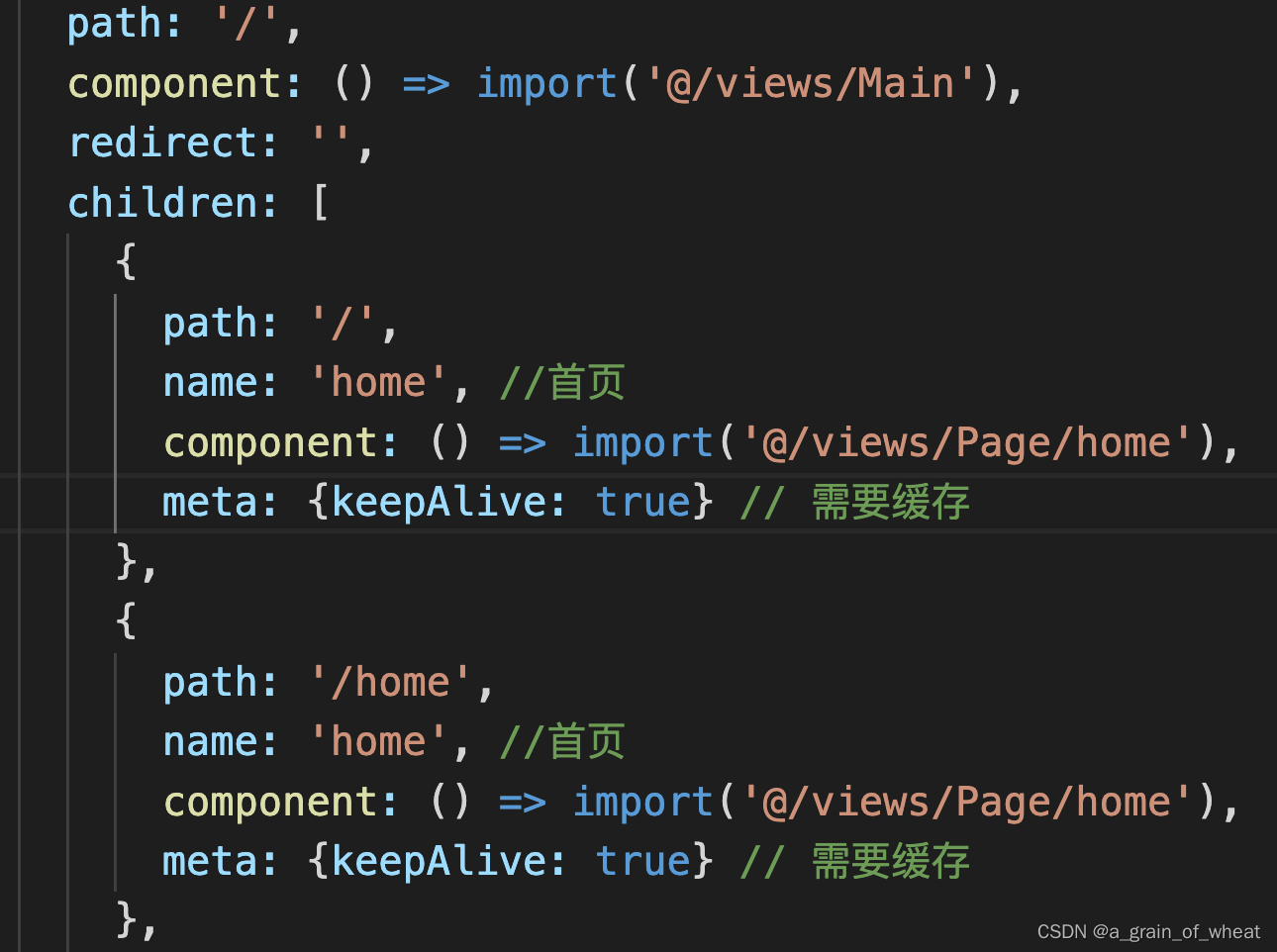
关于vant 的tabbar功能
1、想要实现tabbar页面A,其他的页面B(非tabbar页面)。 从A页面进入B页面,底部的active选中效果应该被取消掉,但是还是选中A。 按照官网的说法有两个方法 一、根据path路径 二、自定义的model 但是!但是…...

:style动态绑定,但只要页面发生变化就会执行一次方法
1、问题 开发过程中有个需求是遍历列表绘制div,div的样式是后端接口传来的,一开始这种写法,:style“formatStyle(item)”,写在了模板中 这样写发现一个问题,只要页面发生重绘,比如页面输入框输入数字&…...
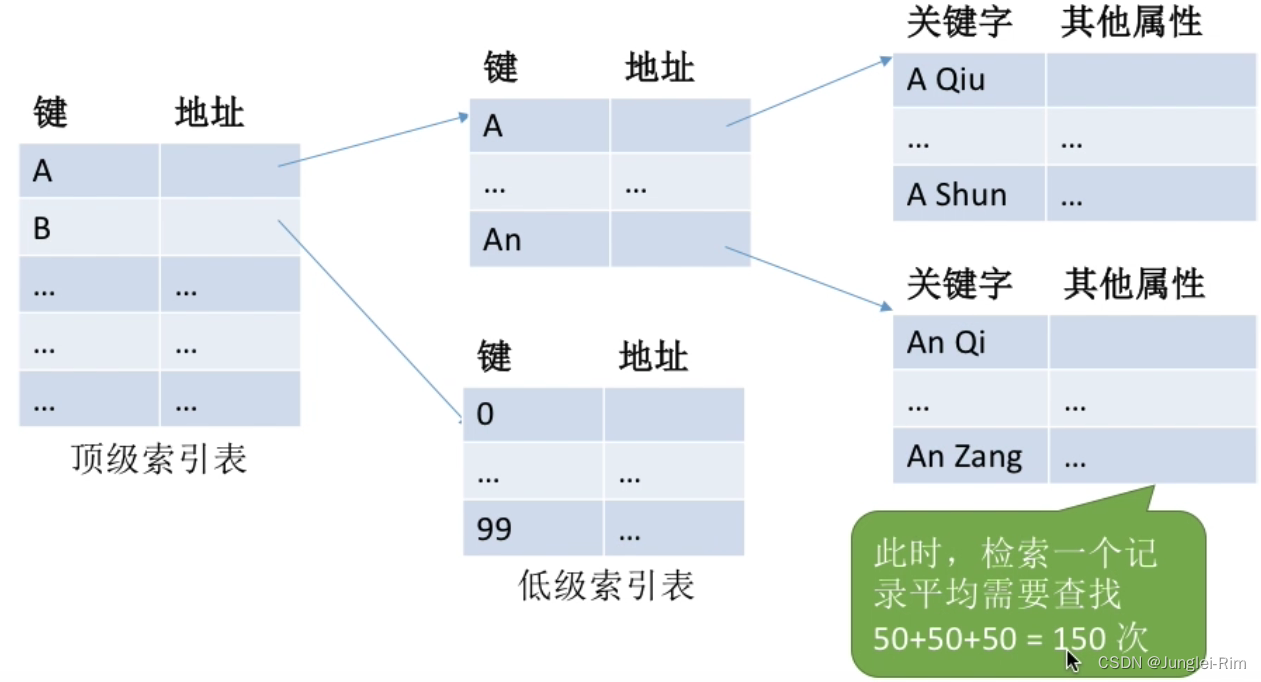
文件的逻辑结构(顺序文件,索引文件)
所谓的“逻辑结构”,就是指在用户看来,文件内部的数据应该是如何组织起来的。 而“物理结构”指的是在操作系统看来,文件的数据是如何存放在外存中的。 1.无结构文件 无结构文件:文件内部的数据就是一系列二进制流或字符流组成。无明显的逻…...

suricata匹配从入门到精通(五)----二次开发保护规则库
0x00 背景 开源的suricata资源包是没有做加密处理,如果想要保护资源包,需要二次开发修改suricata源码。 本文基于suricata6.0.1 版本https://github.com/OISF/suricata/archive/refs/tags/suricata-6.0.1.zip二开。 0x01 实践 通过debug,跟规则处理相关需要修改2个地方。…...
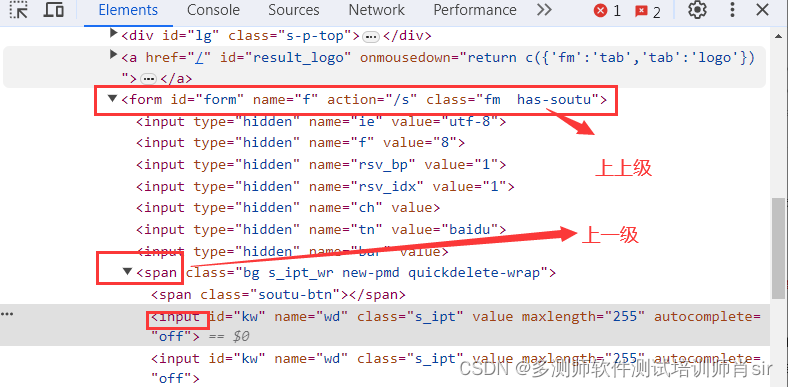
软件测试肖sir__python之ui自动化定位方法(2)
Selenium中元素定位方法 一、定位方法 要实现UI自动化,就必须学会定位web页面元素,Selenium核心 webdriver模块提供了9种定位元素方法: 定位方式 提供方法 id定位 find_element_by_id() name定位 find_element_by_name() class定位 find_elem…...
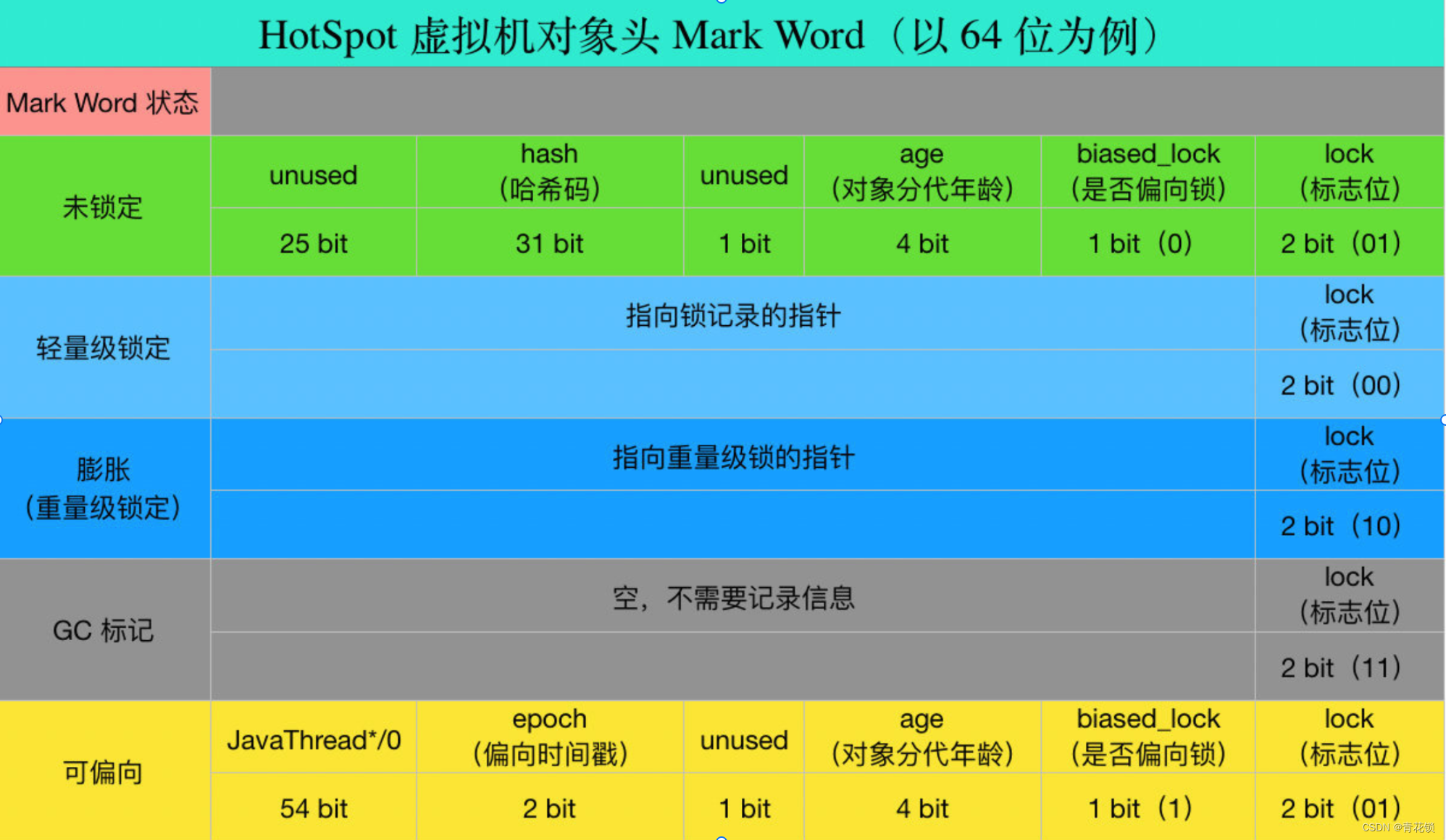
【JVM面试题】JVM分代年龄为何是15次?能设置为16吗?
系列文章目录 【JVM系列】第一章 运行时数据区 【JVM面试题】第二章 从JDK7 到 JDK8, JVM为啥用元空间替换永久代? 【JVM面试题】第三章 JVM分代年龄为何是15次?能设置为16吗? 大家好,我是青花。拥有多项发明专利(都是…...

java三层架构/表现层-业务层-持久层
三层架构 什么是 Java 三层架构 三层架构是指:视图层view(表现层),服务层service(业务逻辑层),持久层Dao(数据访问层), Java的三层架构是指将Java程序分为三…...

视频监控这样做,简单又高效!
随着技术的不断进步,视频监控系统已经变得更加高效和智能,可以提供更全面的监控和分析功能,有助于提高安全性、管理效率和决策支持。 客户案例 超市连锁店 福建某全国性超市连锁店面临高额商品损失、偷窃问题,以及对客户安全和员工…...

掌握 Go 的计时器
简介 定时器是任何编程语言的重要工具,它允许开发人员在特定时间间隔安排任务或执行代码。在 Go 中,定时器是通过 time 包实现的,该包提供了一系列功能来创建、启动、停止和有效处理定时器。我们将探索 Go 中定时器的强大功能,并…...
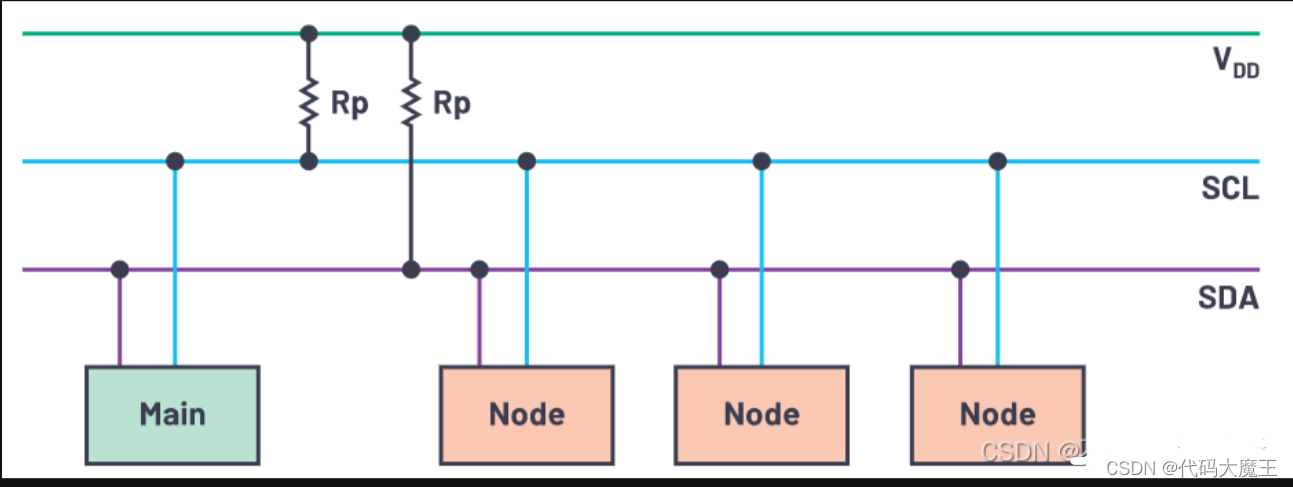
嵌入式软件开发笔试面试
C语言部分: 1.gcc的四步编译过程 1.预处理 展开头文件,删除注释、空行等无用内容,替换宏定义。 gcc -E hello.c -o hello.i 2.编译 检查语法错误,如果有错则报错,没有错误则生成汇编文件。 gcc -S hello.i -o h…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
