sklearn学习-朴素贝叶斯(二)
文章目录
- 一、概率类模型的评估指标
- 1、布里尔分数Brier Score
- 对数似然函数Log Loss
- 二、
- calibration_curve:
- 校准可靠性曲线
- 三、多项式朴素贝叶斯以及其变化
- 四、伯努利朴素贝叶斯
- 五、改进多项式朴素贝叶斯:补集朴素贝叶斯ComplementNB
- 六、文本分类案例
- TF-IDF
- 总结
一、概率类模型的评估指标
1、布里尔分数Brier Score
概率预测的准确程度被称为“校准程度”,是衡量算法预测出的概率和真实结果的差异的一种方式。一种比较常用的指标叫做布里尔分数,它被计算为是概率预测相对于测试样本的均方误差,表示为:
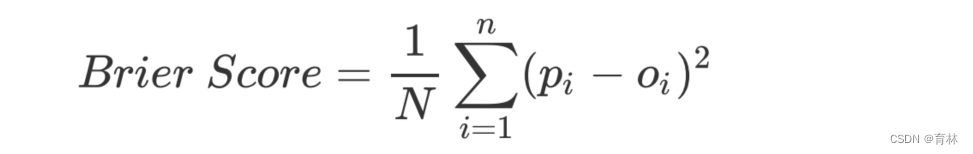
其中N是样本数量, 为朴素贝叶斯预测出的概率, 是样本所对应的真实结果,只能取到0或者1,如果事件发生则为1,如果不发生则为0。这个指标衡量了我们的概率距离真实标签结果的差异,其实看起来非常像是均方误差。布里尔分数的范围是从0到1,分数越高则预测结果越差劲,校准程度越差,因此布里尔分数越接近0越好。由于它的本质也是在衡量一种损失,所以在sklearn当中,布里尔得分被命名为brier_score_loss。
对数似然函数Log Loss
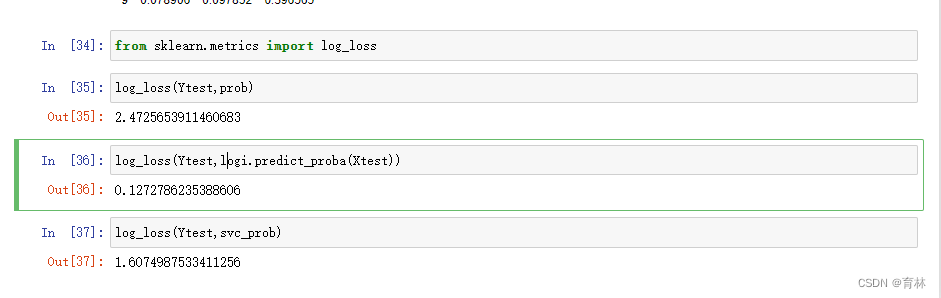
另一种常用的概率损失衡量是对数损失(log_loss),又叫做对数似然,逻辑损失或者交叉熵损失,它是多元逻辑回归以及一些拓展算法,比如神经网络中使用的损失函数。它被定义为,对于一个给定的概率分类器,在预测概率为条件的情况下,真实概率发生的可能性的负对数(如何得到这个损失函数的证明过程和推导过程在逻辑回归的章节中有完整得呈现)。由于是损失,因此对数似然函数的取值越小,则证明概率估计越准确,模型越理想。值得注意得是,对数损失只能用于评估分类型模型。对于一个样本,如果样本的真实标签yture 在{0,1}中取值,并且这个样本在类别1下的概率估计为ypred ,则这个样本所对应的对数损失是:
二、
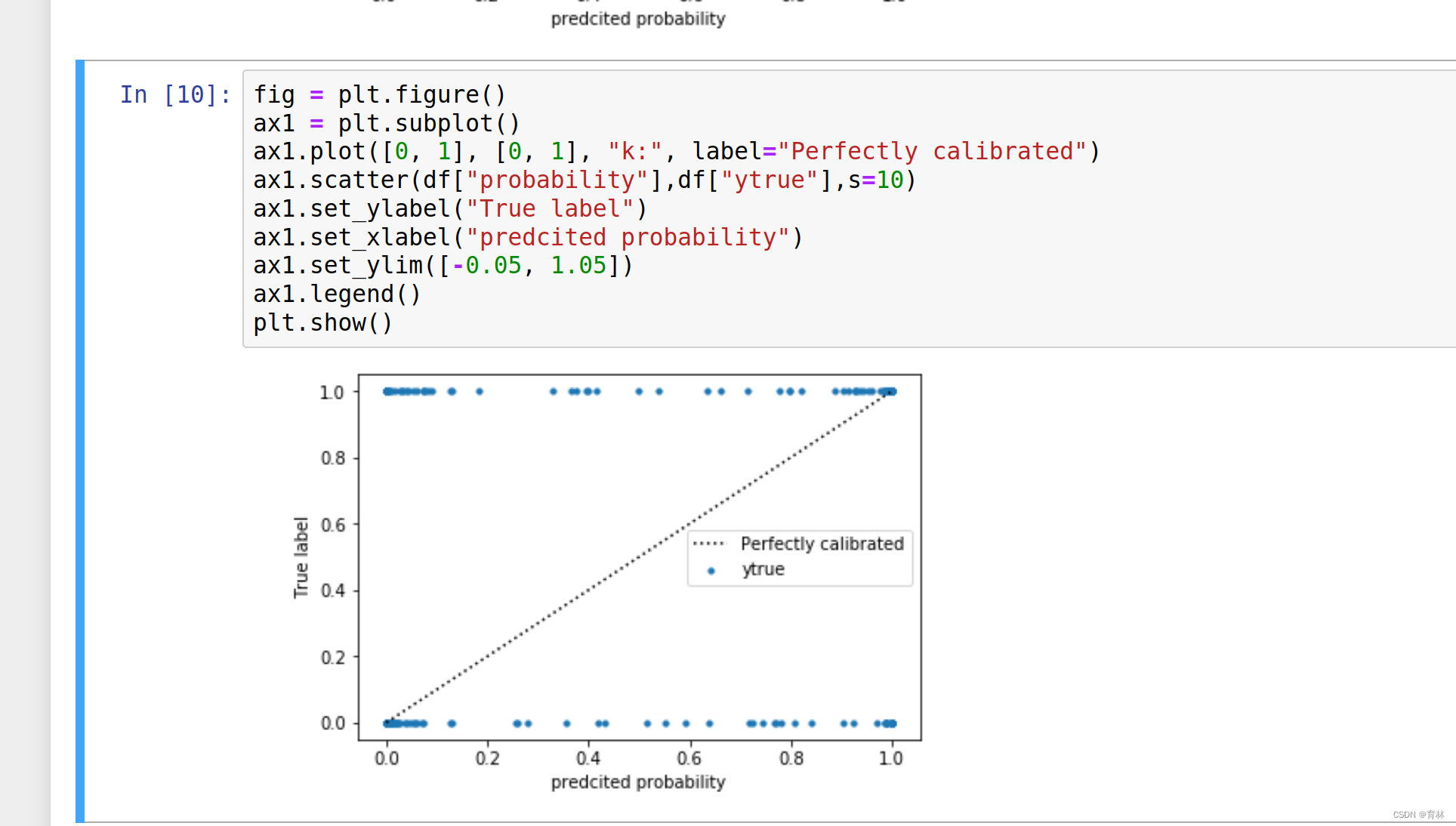
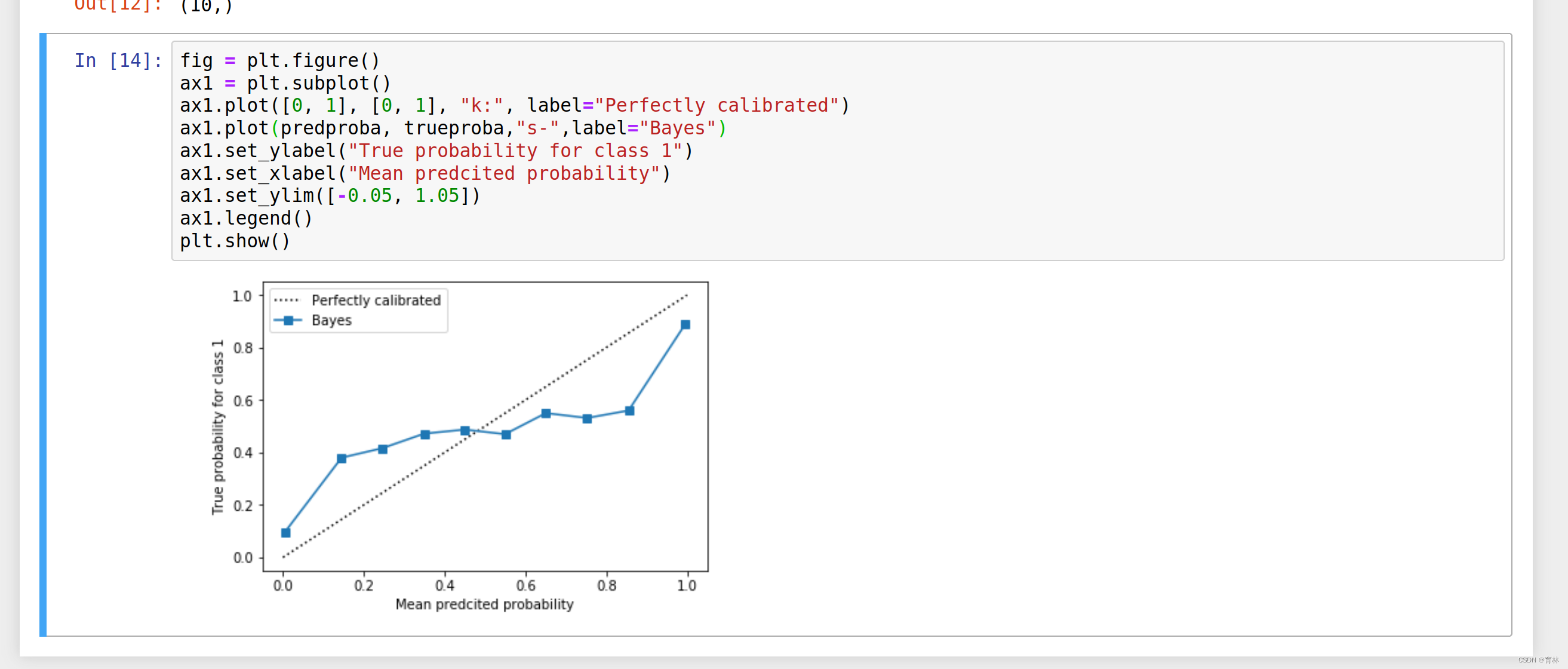
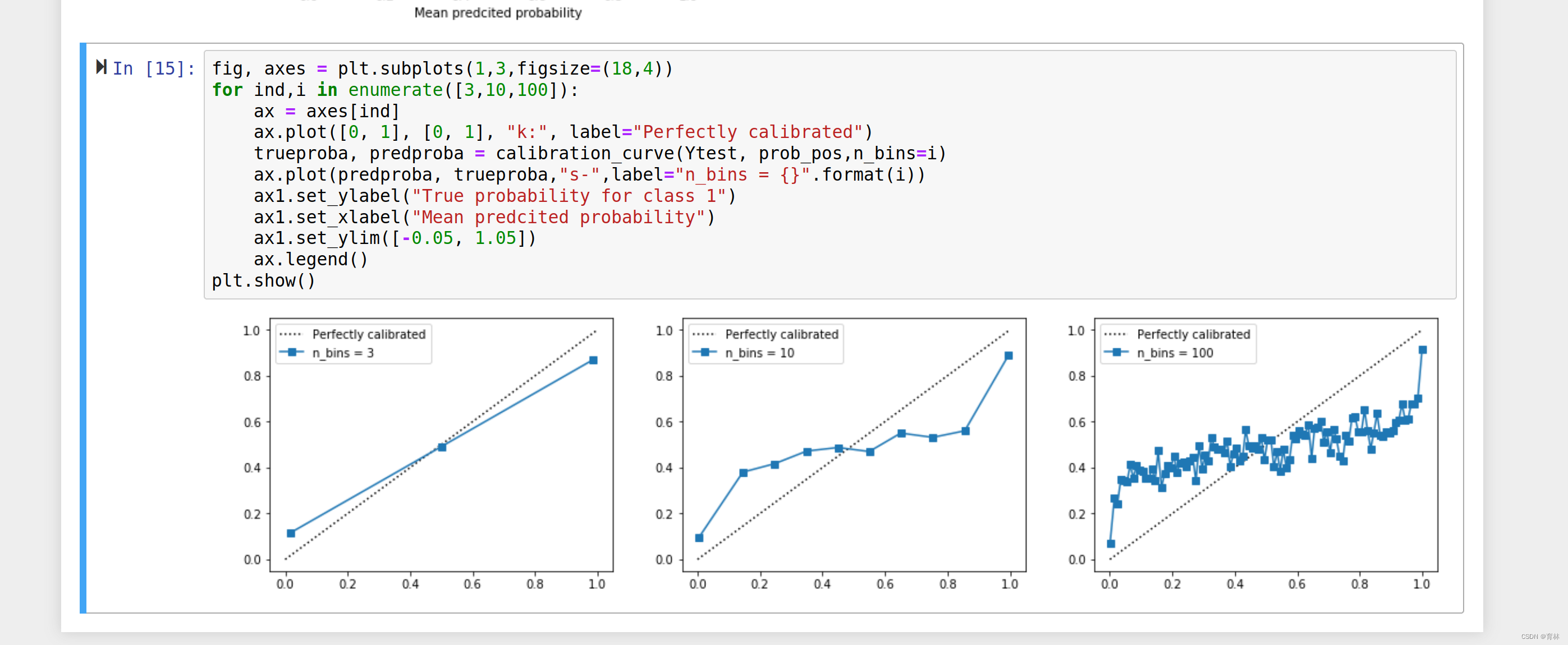
calibration_curve:

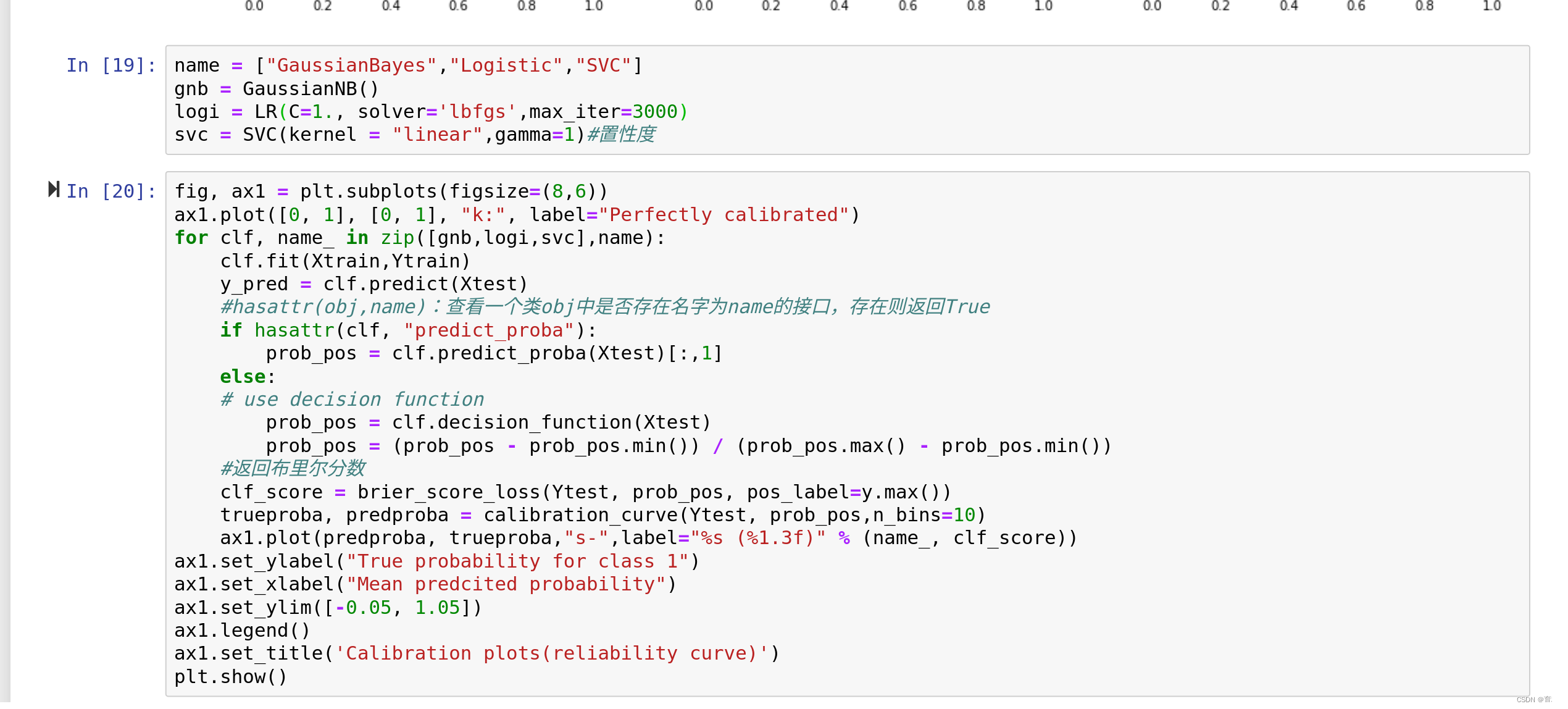
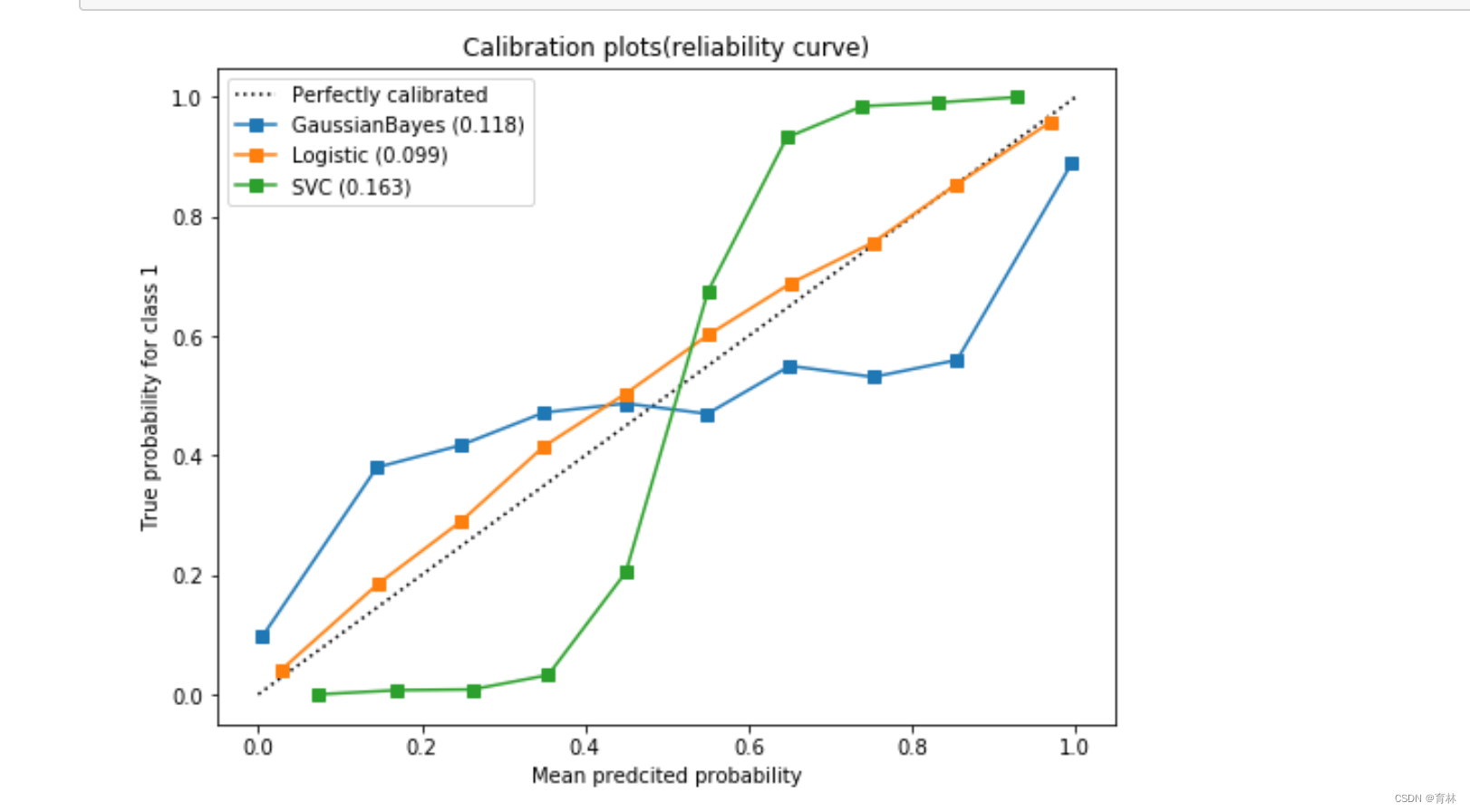
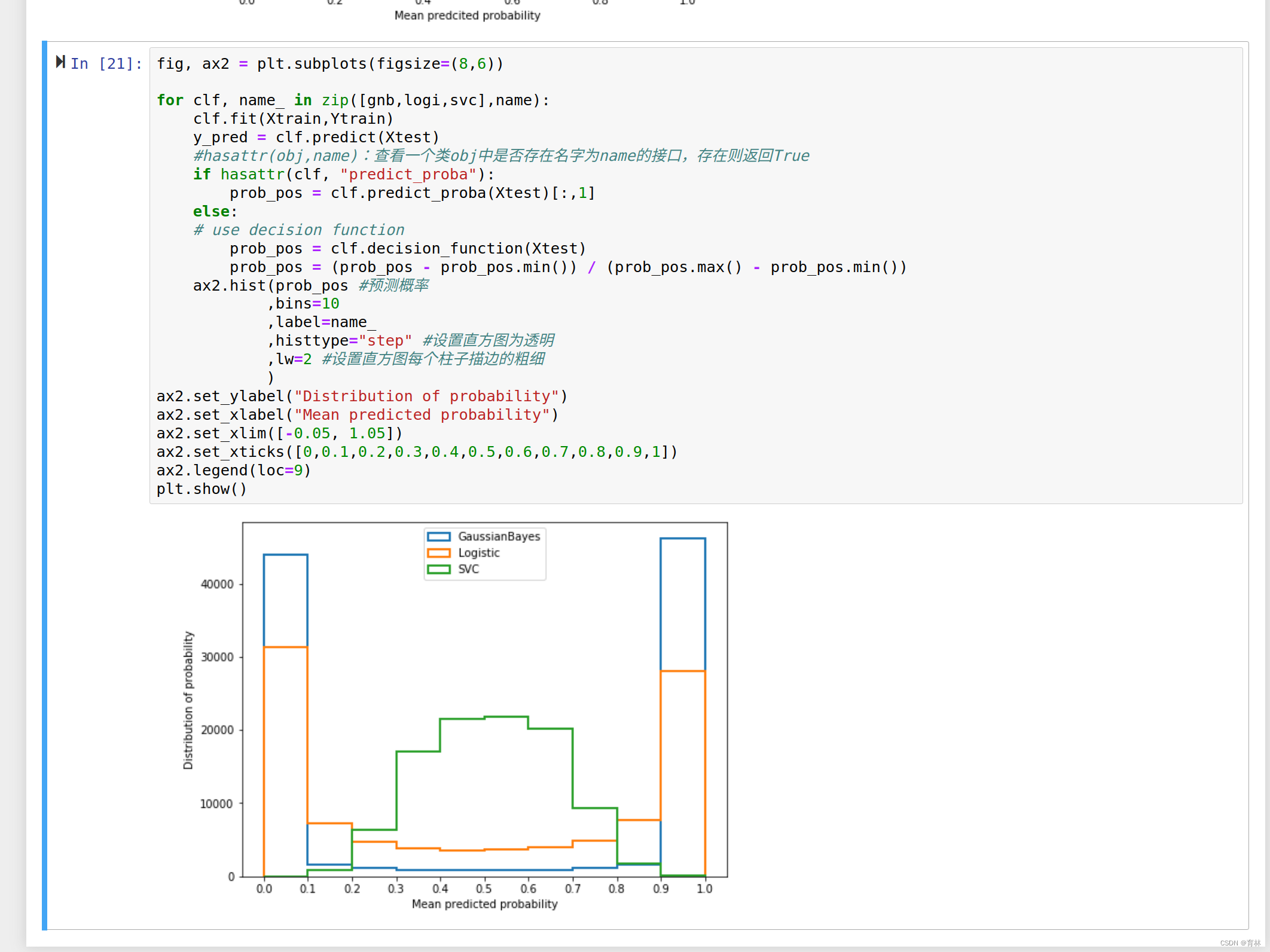
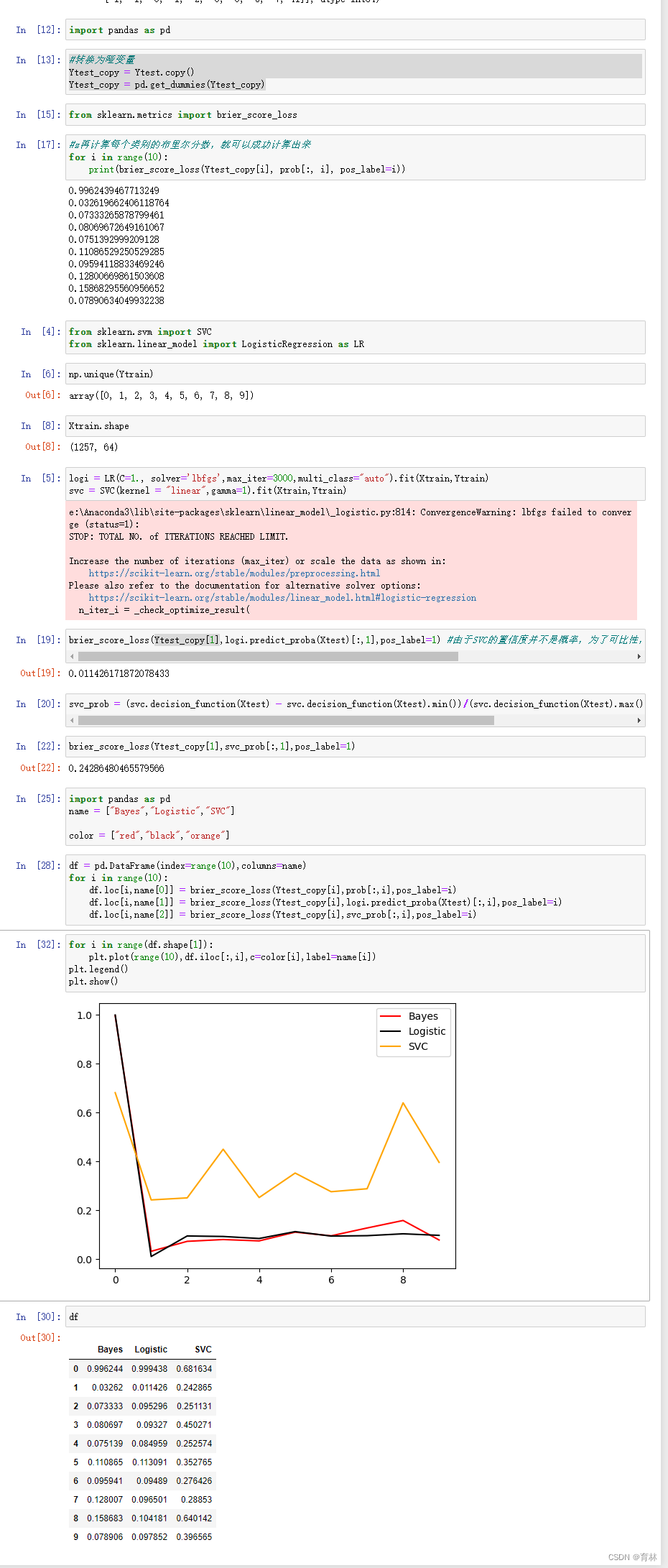
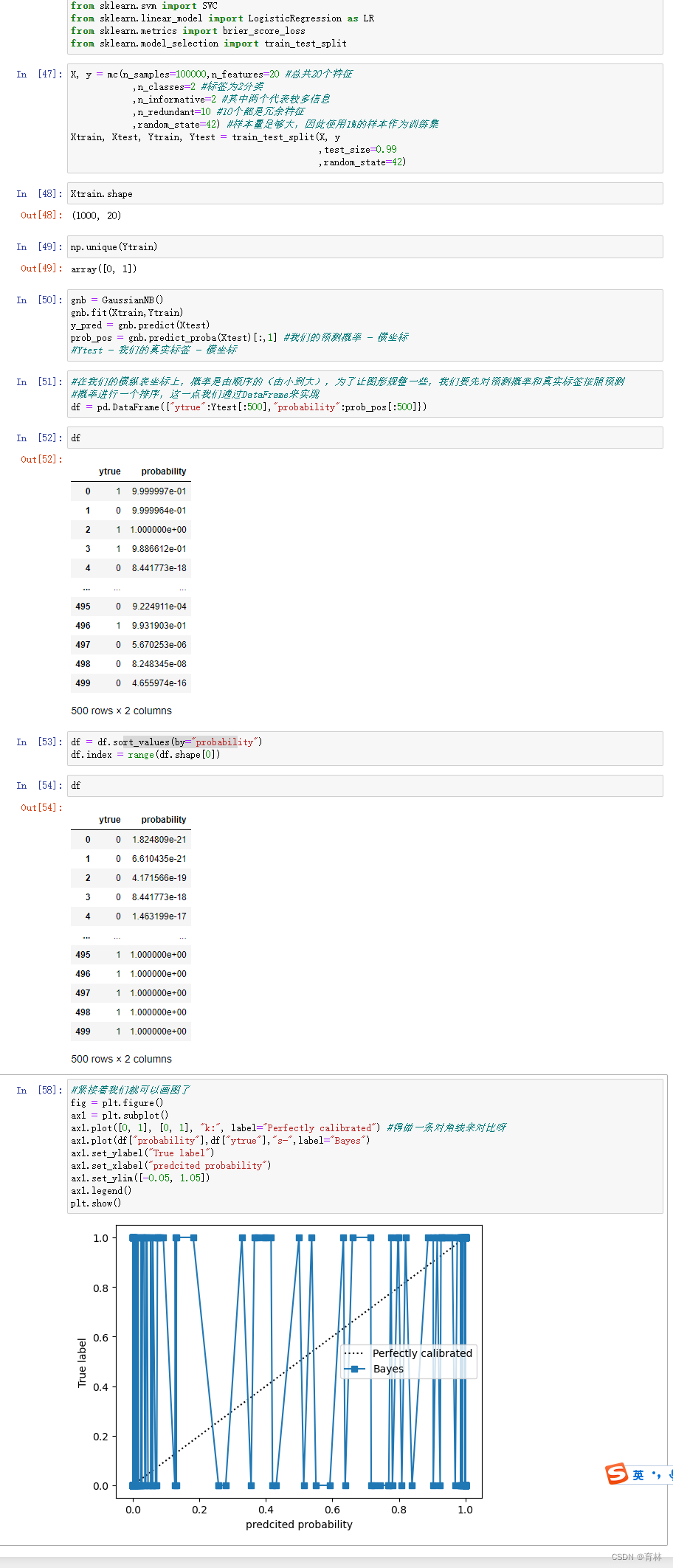
可以看到,高斯贝叶斯的概率分布是两边非常高,中间非常低,几乎90%以上的样本都在0和1的附近,可以说是置信度最高的算法,但是贝叶斯的布里尔分数却不如逻辑回归,这证明贝叶斯中在0和1附近的样本中有一部分是被分错的。支持向量贝叶斯完全相反,明显是中间高,两边低,类似于正态分布的状况,证明了我们刚才所说的,大部分样本都在决策边界附近,置信度都徘徊在0.5左右的情况。而逻辑回归位于高斯朴素贝叶斯和支持向量机的中间,即没有太多的样本过度靠近0和1,也没有形成像支持向量机那样的正态分布。一个比较健康的正样本的概率分布,就是逻辑回归的直方图显示出来的样子。
避免混淆:概率密度曲线和概率分布直方图
大家也许还记得我们说过,我们是假设样本的概率分布为高斯分布,然后使用高斯的方程来估计连续型变量的概率。怎么现在我们绘制出的概率分布结果中,高斯普斯贝叶斯的概率分布反而完全不是高斯分布了呢?注意,千万不要把概率密度曲线和概率分布直方图混淆。
在称重汉堡的时候所绘制的曲线,是概率密度曲线,横坐标是样本的取值,纵坐标是落在这个样本取值区间中的样本个数,衡量的是每个X的取值区间之内有多少样本。服从高斯分布的是X的取值上的样本分布。
现在我们的概率分布直方图,横坐标是概率的取值[0,1],纵坐标是落在这个概率取值范围中的样本的个数,衡量的是每个概率取值区间之内有多少样本。这个分布,是没有任何假设的。
校准可靠性曲线
在这里,我主要来为大家展示如果使用sklearn中的概率校正类CalibratedClassifierCV来对二分类情况下的数据集进行概率校正。
class sklearn.calibration.CalibratedClassifierCV (base_estimator=None, method=’sigmoid’, cv=’warn’)这是一个带交叉验证的概率校准类,它使用交叉验证生成器,对交叉验证中的每一份数据,它都在训练样本上进行模型参数估计,在测试样本上进行概率校准,然后为我们返回最佳的一组参数估计和校准结果。每一份数据的预测概率会被求解平均。注意,类CalibratedClassifierCV没有接口decision_function,要查看这个类下校准过后的模型生成的概率,必须调用predict_proba接口。
base_estimator
需要校准其输出决策功能的分类器,必须存在predict_proba或decision_function接口。 如果参数cv = prefit,分类器必须已经拟合数据完毕。
cv
整数,确定交叉验证的策略。可能输入是:
None,表示使用默认的3折交叉验证
任意整数,指定折数
对于输入整数和None的情况下来说,如果时二分类,则自动使用类sklearn.model_selection.StratifiedKFold进
行折数分割。如果y是连续型变量,则使用sklearn.model_selection.KFold进行分割。
已经使用其他类建好的交叉验证模式或生成器cv
可迭代的,已经分割完毕的测试集和训练集索引数组
输入"prefit",则假设已经在分类器上拟合完毕数据。在这种模式下,使用者必须手动确定用来拟合分类器的数
据与即将倍校准的数据没有交集
在版本0.20中更改:在0.22版本中输入“None”,将由使用3折交叉验证改为5折交叉验证
method
进行概率校准的方法,可输入"sigmoid"或者"isotonic"
输入’sigmoid’,使用基于Platt的Sigmoid模型来进行校准
输入’isotonic’,使用等渗回归来进行校准
当校准的样本量太少(比如,小于等于1000个测试样本)的时候,不建议使用等渗回归,因为它倾向于过拟合。样本量过少时请使用sigmoids,即Platt校准。
我们依然来使用之前建立的数据集。
def plot_calib(models,name,Xtrain,Xtest,Ytrain,Ytest,n_bins=10):import matplotlib.pyplot as pltfrom sklearn.metrics import brier_score_lossfrom sklearn.calibration import calibration_curvefig, (ax1, ax2) = plt.subplots(1, 2,figsize=(20,6))ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")for clf, name_ in zip(models,name):clf.fit(Xtrain,Ytrain)y_pred = clf.predict(Xtest)#hasattr(obj,name):查看一个类obj中是否存在名字为name的接口,存在则返回Trueif hasattr(clf, "predict_proba"):prob_pos = clf.predict_proba(Xtest)[:,1]else:# use decision functionprob_pos = clf.decision_function(Xtest)prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())#返回布里尔分数clf_score = brier_score_loss(Ytest, prob_pos, pos_label=y.max())trueproba, predproba = calibration_curve(Ytest, prob_pos,n_bins=n_bins)ax1.plot(predproba, trueproba,"s-",label="%s (%1.3f)" % (name_, clf_score))ax2.hist(prob_pos, range=(0, 1), bins=n_bins, label=name_,histtype="step",lw=2)ax2.set_ylabel("Distribution of probability")ax2.set_xlabel("Mean predicted probability")ax2.set_xlim([-0.05, 1.05])ax2.legend(loc=9)ax2.set_title("Distribution of probablity")ax1.set_ylabel("True probability for class 1")ax1.set_xlabel("Mean predcited probability")ax1.set_ylim([-0.05, 1.05])ax1.legend()ax1.set_title('Calibration plots(reliability curve)')plt.show()
from sklearn.calibration import CalibratedClassifierCV
name = ["GaussianBayes","Logistic","Bayes+isotonic","Bayes+sigmoid"]
gnb = GaussianNB()
models = [gnb,LR(C=1., solver='lbfgs',max_iter=3000)#定义两种校准方式,CalibratedClassifierCV(gnb, cv=2, method='isotonic'),CalibratedClassifierCV(gnb, cv=2, method='sigmoid')]
plot_calib(models,name,Xtrain,Xtest,Ytrain,Ytest)
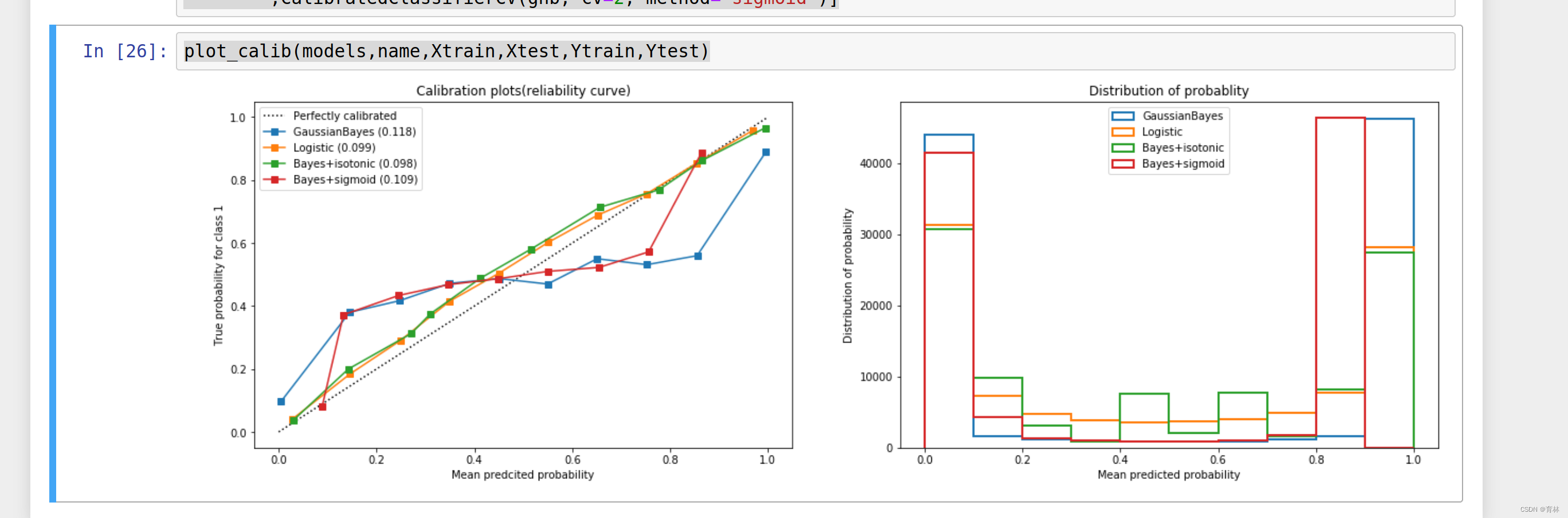
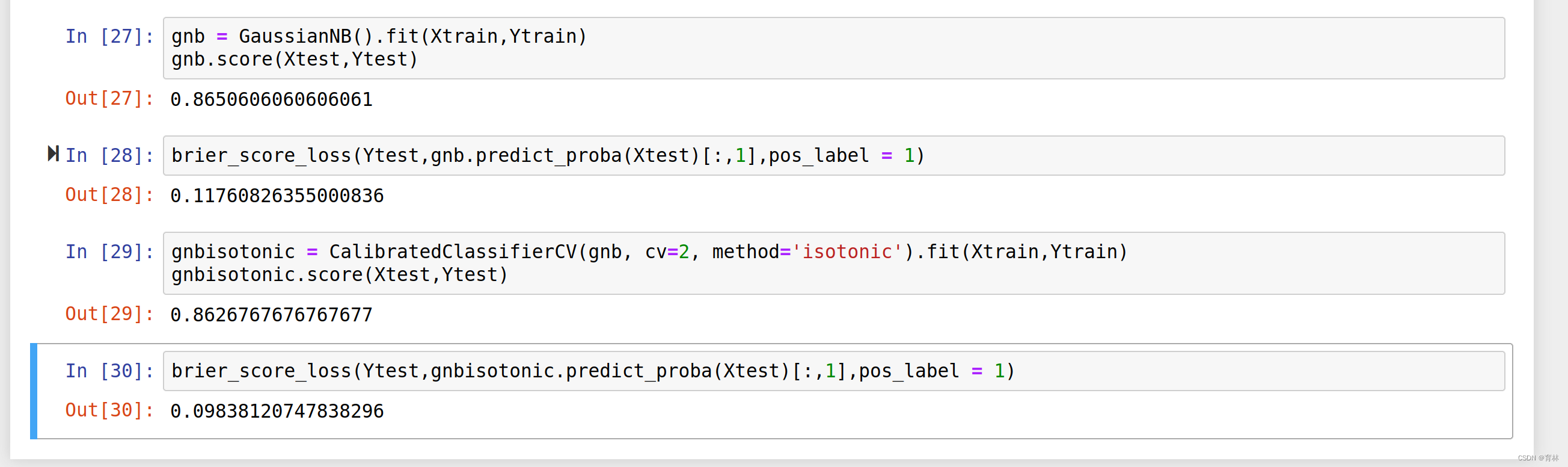
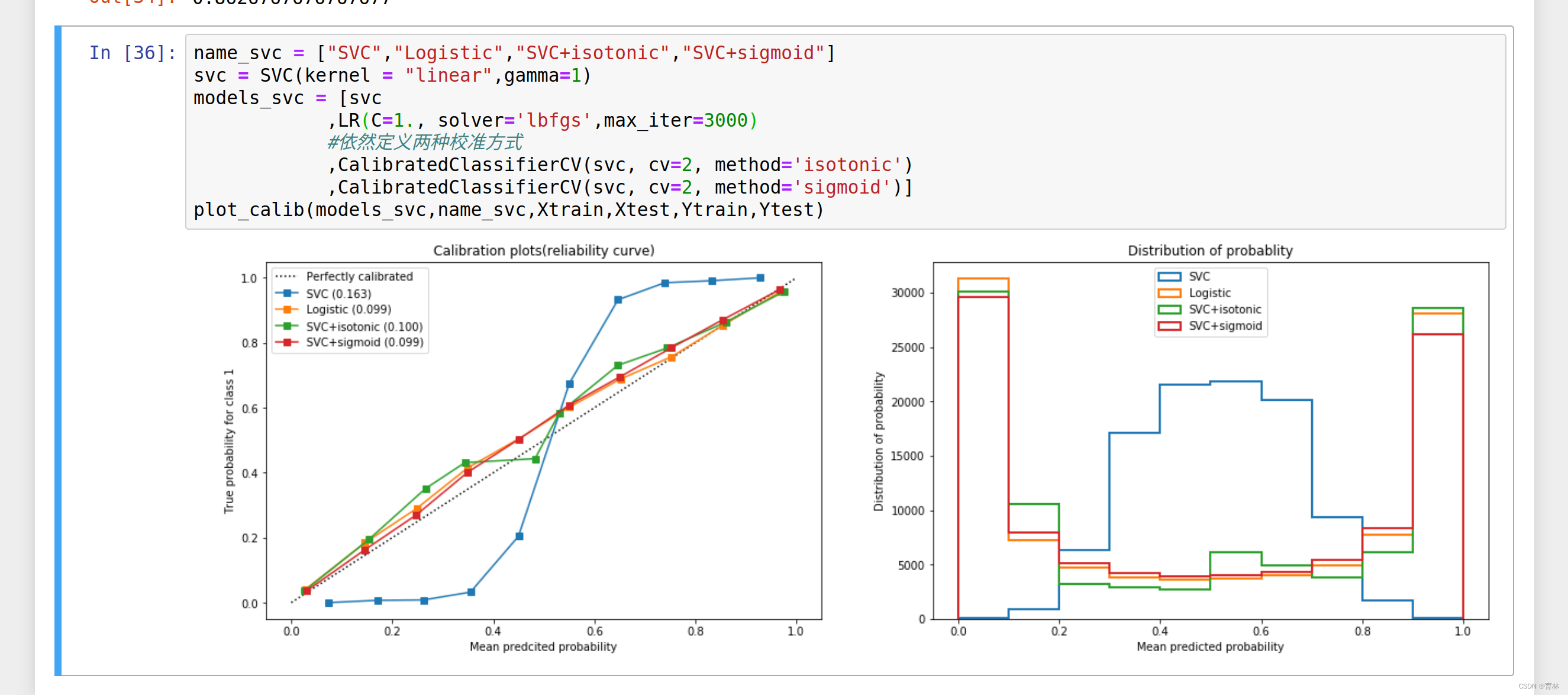
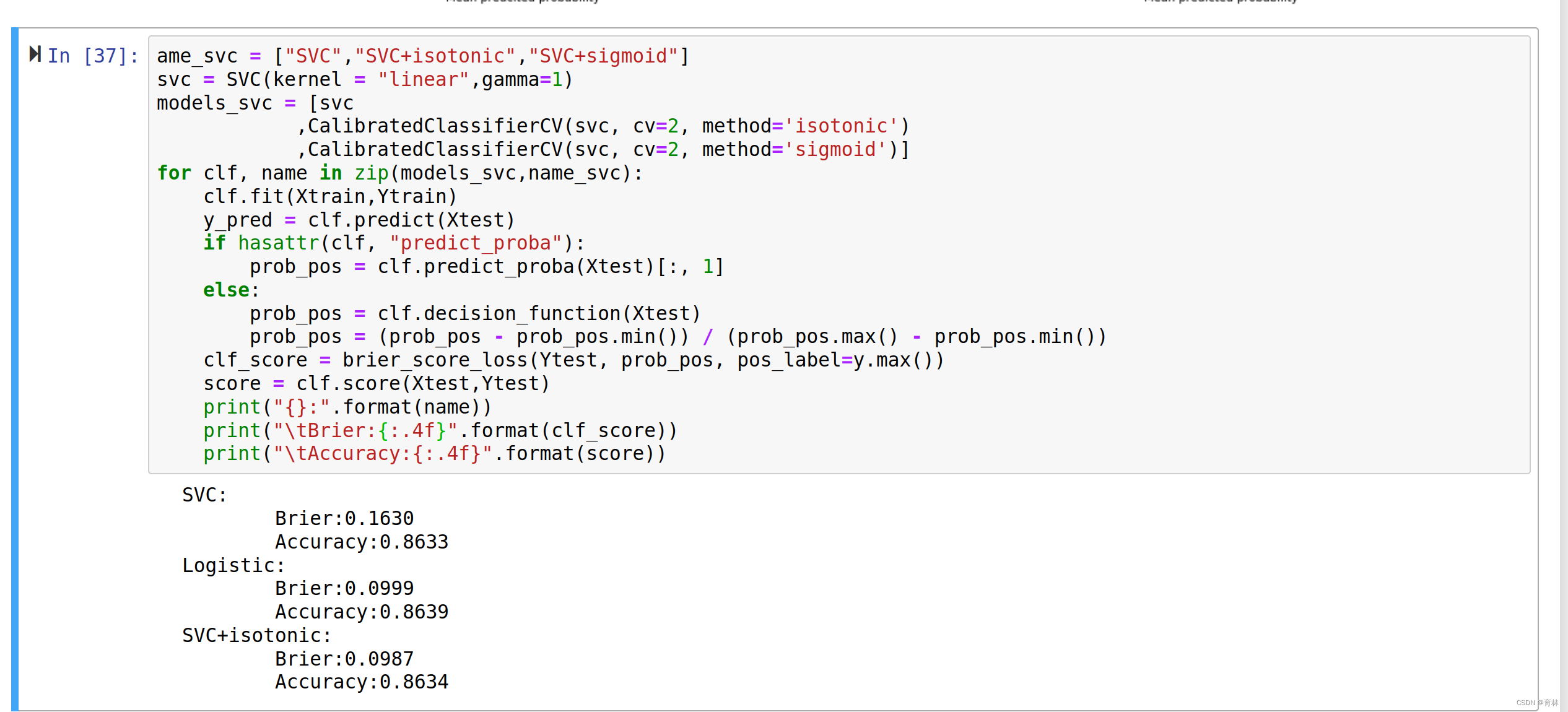 可以看到,对于SVC来说,两种校正都改善了准确率和布里尔分数。可见,概率校正对于SVC非常有效。这也说明,概率校正对于原本的可靠性曲线是形容Sigmoid形状的曲线的算法比较有效。
可以看到,对于SVC来说,两种校正都改善了准确率和布里尔分数。可见,概率校正对于SVC非常有效。这也说明,概率校正对于原本的可靠性曲线是形容Sigmoid形状的曲线的算法比较有效。
在现实中,我们可以选择调节模型的方向,我们不一定要追求最高的准确率或者追求概率拟合最好,我们可以根据自己的需求来调整模型。当然,对于概率类模型来说,由于可以调节的参数甚少,所以我们更倾向于追求概率拟合,并使用概率校准的方式来调节模型。如果你的确希望追求更高的准确率和Recall,可以考虑使用天生就非常准确的概率类模型逻辑回归,也可以考虑使用除了概率校准之外还有很多其他参数可调的支持向量机分类器。
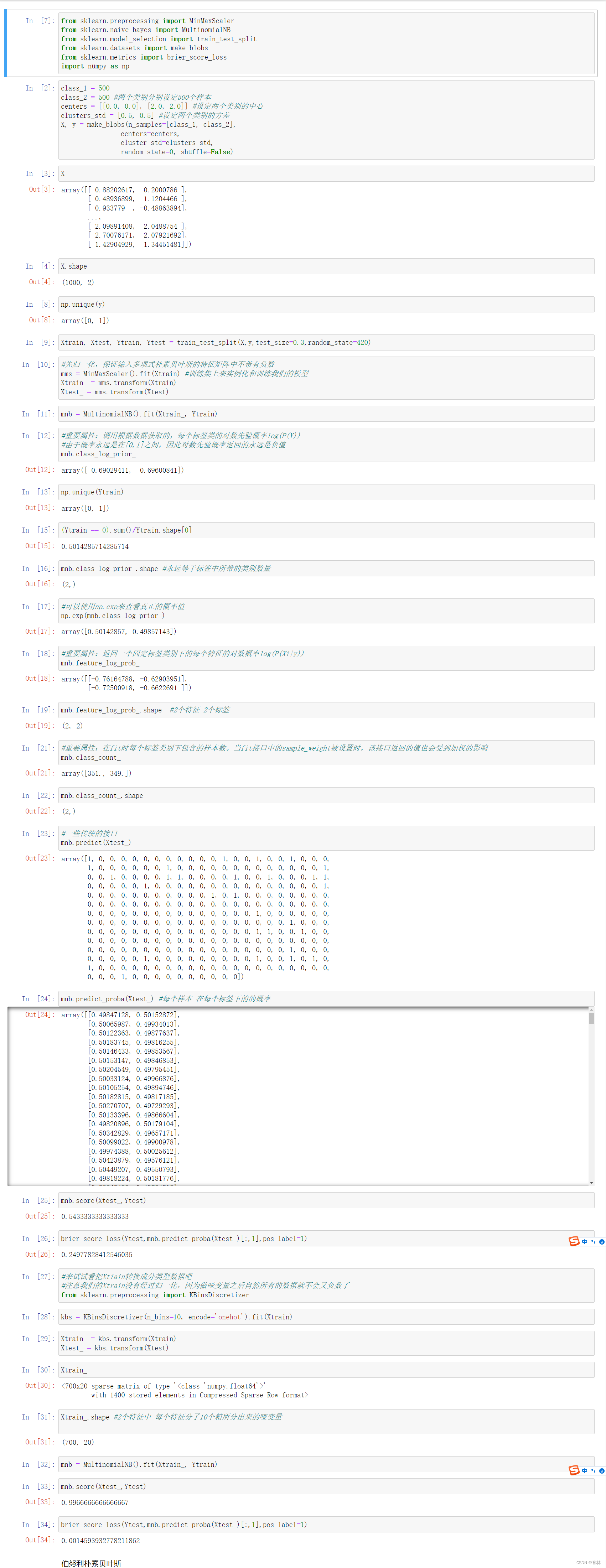
三、多项式朴素贝叶斯以及其变化
四、伯努利朴素贝叶斯
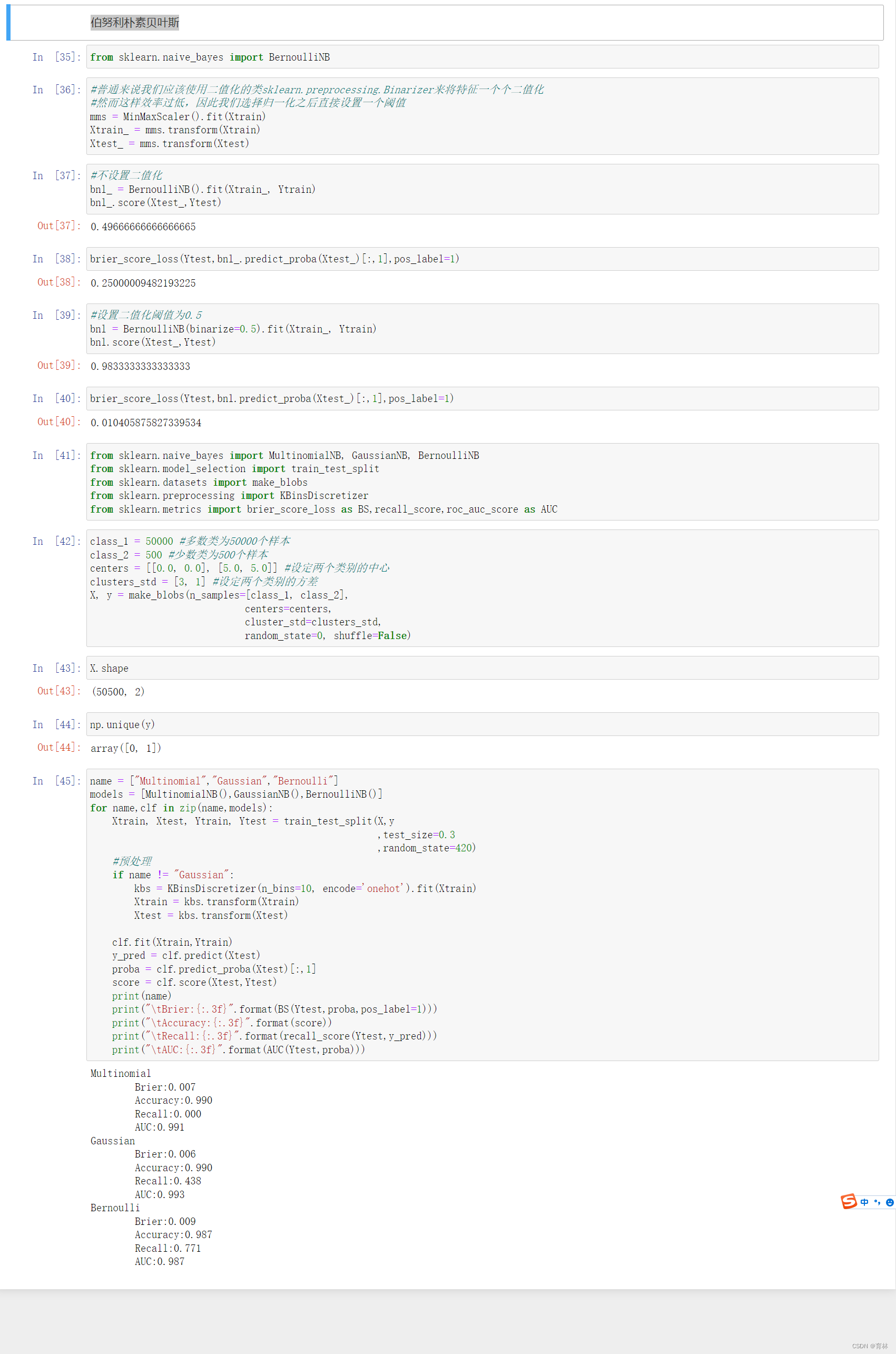
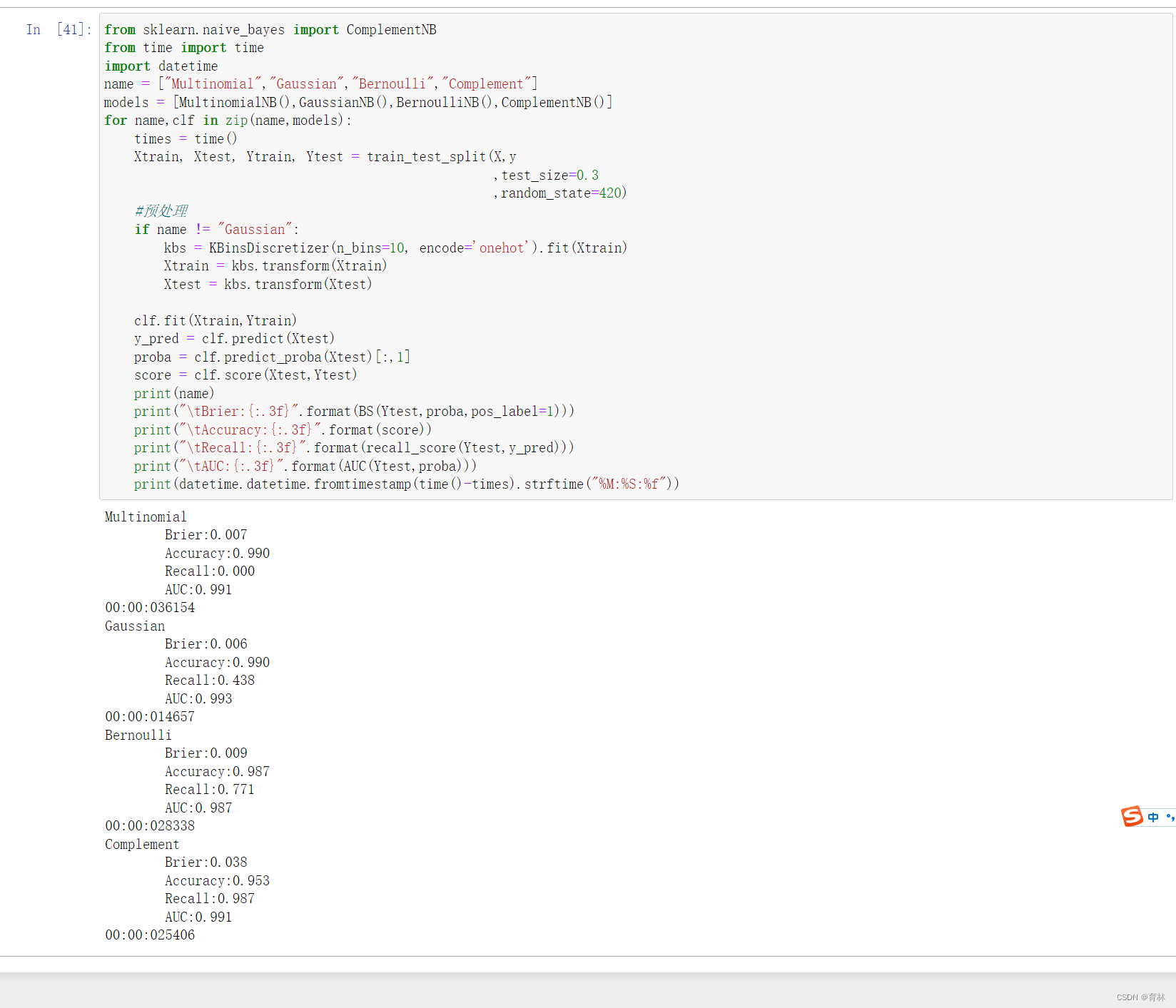
从结果上来看,多项式朴素贝叶斯判断出了所有的多数类样本,但放弃了全部的少数类样本,受到样本不均衡问题影响最严重。高斯比多项式在少数类的判断上更加成功一些,至少得到了43.8%的recall。伯努利贝叶斯虽然整体的准确度和布里尔分数不如多项式和高斯朴素贝叶斯和,但至少成功捕捉出了77.1%的少数类。可见,伯努利贝叶斯最能够忍受样本不均衡问题。
可是,伯努利贝叶斯只能用于处理二项分布数据,在现实中,强行将所有的数据都二值化不会永远得到好结果,在我们有多个特征的时候,我们更需要一个个去判断究竟二值化的阈值该取多少才能够让算法的效果优秀。这样做无疑是非常低效的。那如果我们的目标是捕捉少数类,我们应该怎么办呢?高斯朴素贝叶斯的效果虽然比多项式好,但是也没有好到可以用来帮助我们捕捉少数类的程度——43.8%,还不如抛硬币的结果。因此,孜孜不倦的统计学家们改进了朴素贝叶斯算法,修正了包括无法处理样本不平衡在内的传统朴素贝叶斯的众多缺点,得到了新兴贝叶斯算法:补集朴素贝叶斯
五、改进多项式朴素贝叶斯:补集朴素贝叶斯ComplementNB
六、文本分类案例
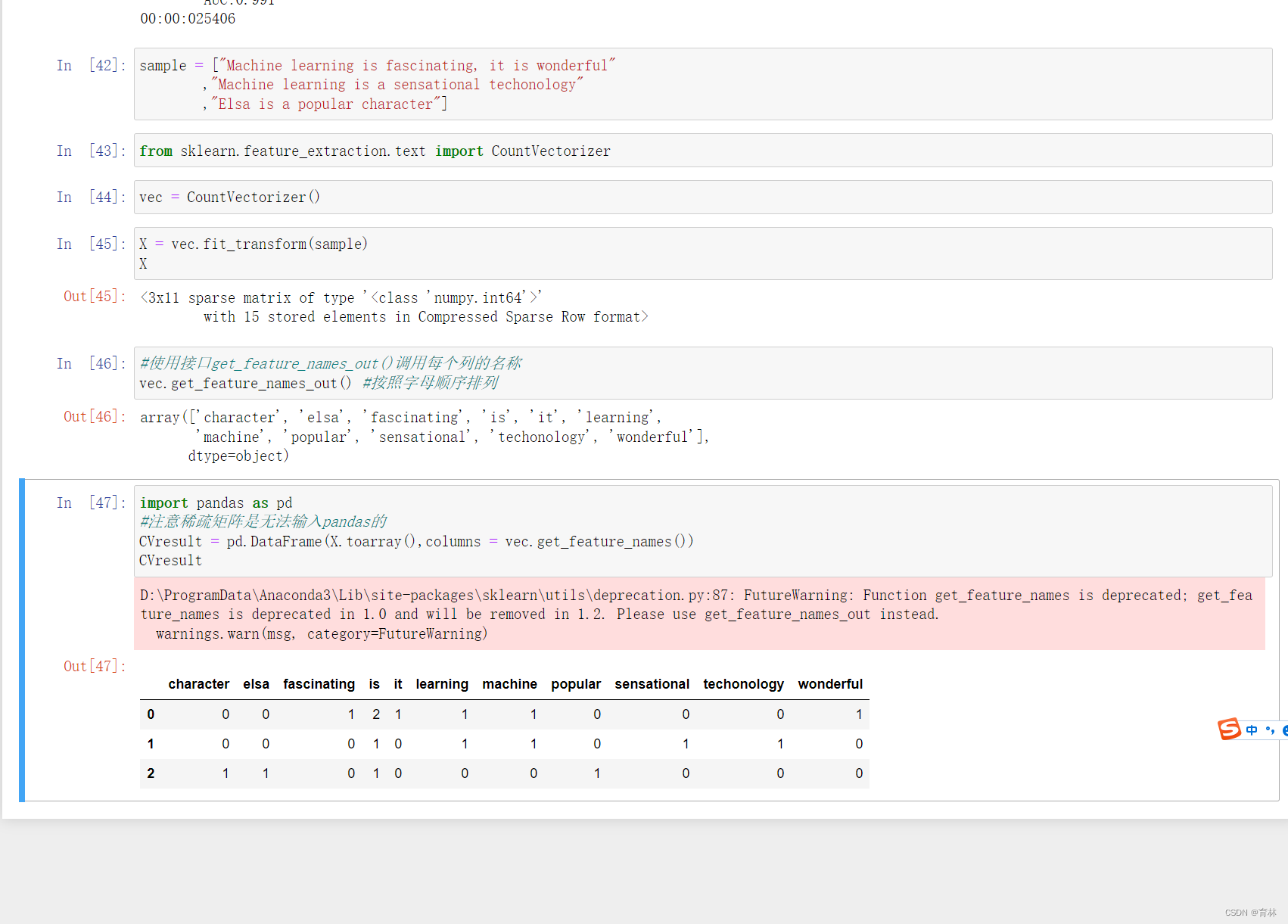
TF-IDF
TF-IDF全称term frequency-inverse document frequency,词频逆文档频率,是通过单词在文档中出现的频率来衡量其权重,也就是说,IDF的大小与一个词的常见程度成反比,这个词越常见,编码后为它设置的权重会倾向于越小,以此来压制频繁出现的一些无意义的词。在sklearn当中,我们使用feature_extraction.text中类TfidfVectorizer来执行这种编码。
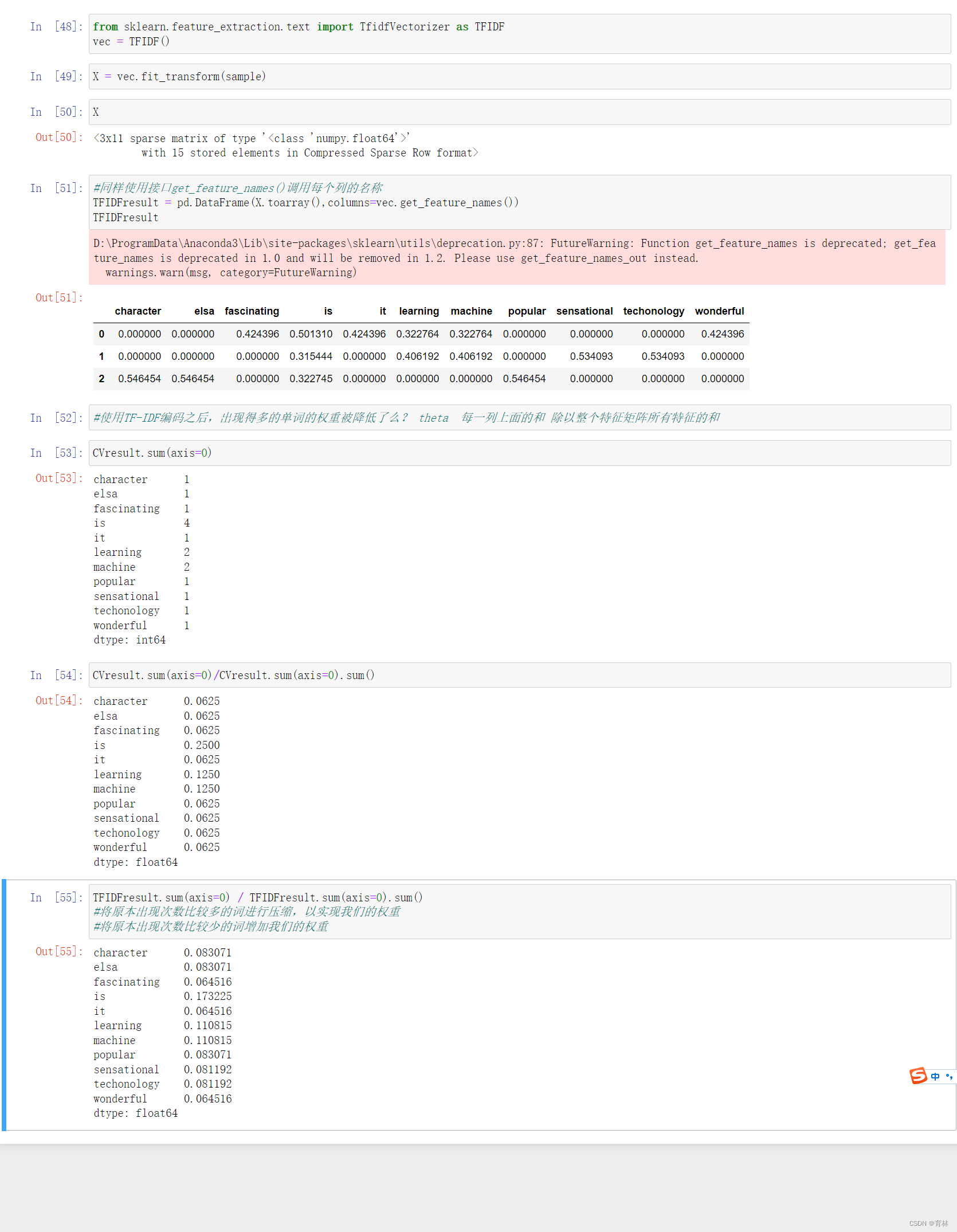
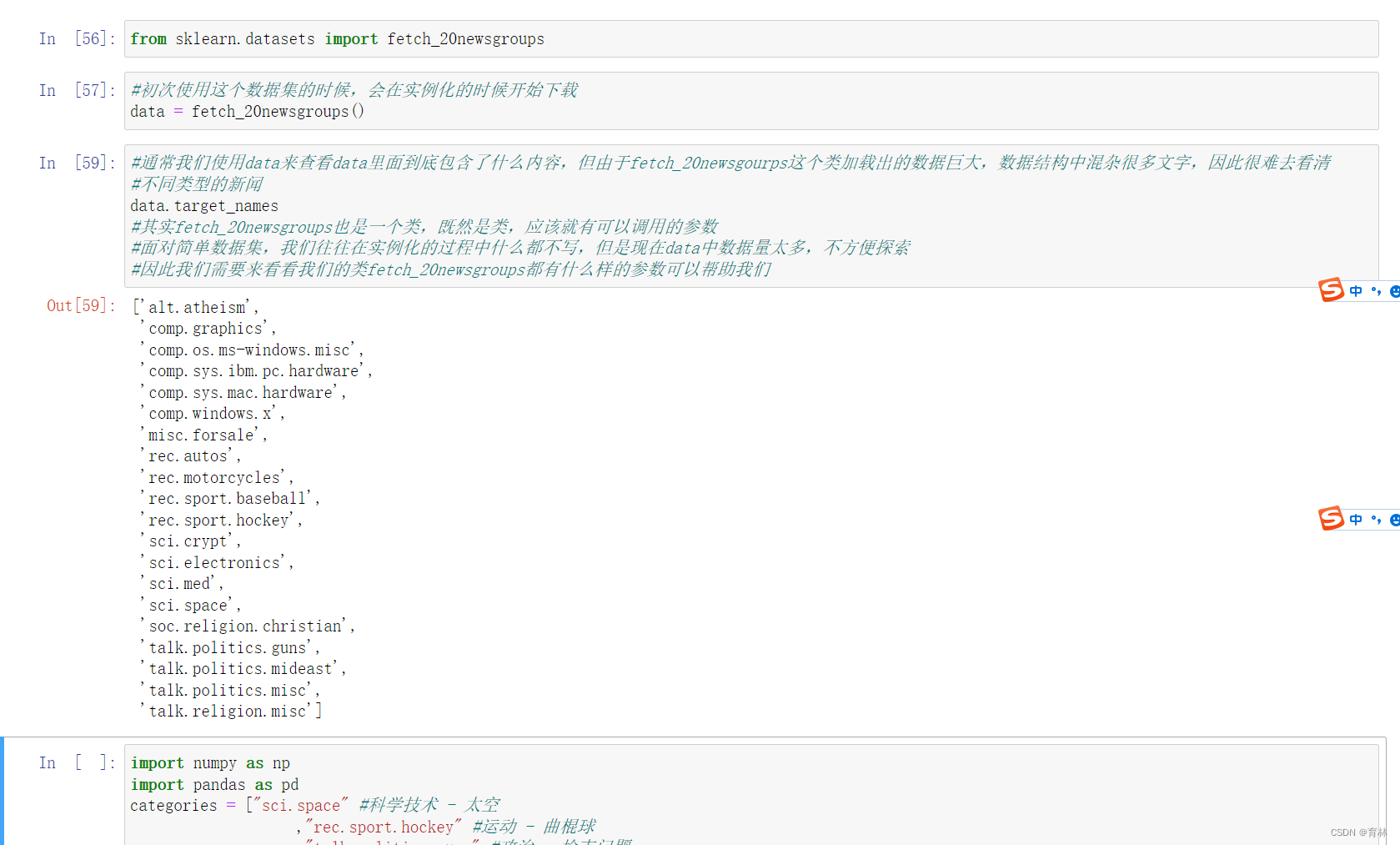
sklearn.datasets.fetch_20newsgroups (data_home=None, subset=’train’, categories=None, shuffle=True,
random_state=42, remove=(), download_if_missing=True)

总结
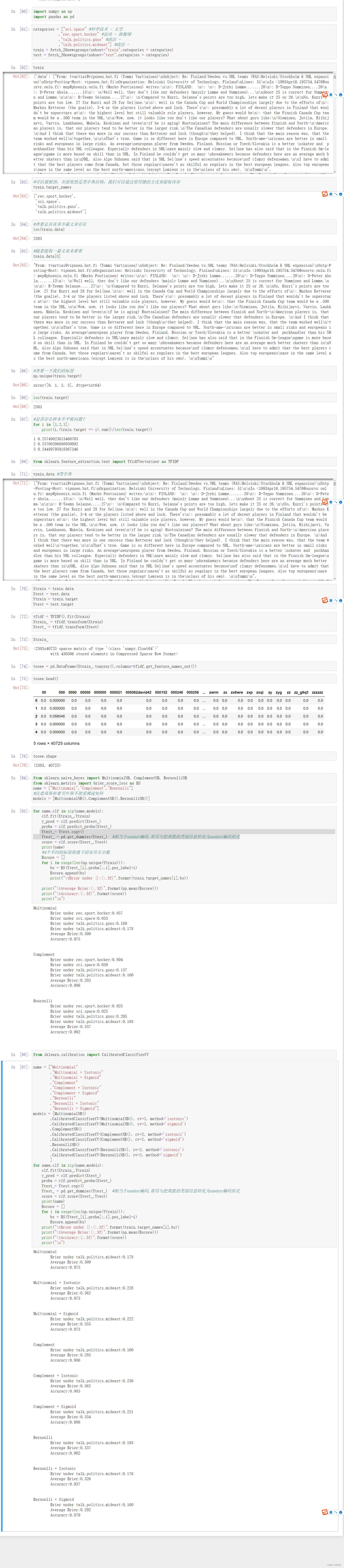
可以观察到,多项式分布下无论如何调整,算法的效果都不如补集朴素贝叶斯来得好。因此我们在分类的时候,应该选择补集朴素贝叶斯。对于补集朴素贝叶斯来说,使用Sigmoid进行概率校准的模型综合最优秀:准确率最高,对数损失和布里尔分数都在0.1以下,可以说是非常理想的模型了。
对于机器学习而言,朴素贝叶斯也许不是最常用的分类算法,但作为概率预测算法中唯一一个真正依赖概率来进行计算,并且简单快捷的算法,朴素贝叶斯还是常常被人们提起。并且,朴素贝叶斯在文本分类上的效果的确非常优秀。由此可见,只要我们能够提供足够的数据,合理利用高维数据进行训练,朴素贝叶斯就可以为我们提供意想不到的效果。
相关文章:

sklearn学习-朴素贝叶斯(二)
文章目录一、概率类模型的评估指标1、布里尔分数Brier Score对数似然函数Log Loss二、calibration_curve:校准可靠性曲线三、多项式朴素贝叶斯以及其变化四、伯努利朴素贝叶斯五、改进多项式朴素贝叶斯:补集朴素贝叶斯ComplementNB六、文本分类案例TF-ID…...

MySQL_主从复制读写分离
主从复制 概述 主从复制是指将主数据库的DDL和DML操作通过二进制日志传到从库服务器中,然后在从库上对这些日志重新执行(也叫重做),从而使得从库和主库的数据保持同步。 MySQL支持一台主库同时向多台从库进行复制,从…...
shell基础学习
文章目录查看shell解释器写hello world多命令处理执行变量常用系统变量自定义变量撤销变量静态变量变量提升为全局环境变量特殊变量$n$#$* $$?运算符:条件判断比较流程控制语句ifcasefor 循环while 循环read读取控制台输入基本语法:函数系统函数basenamedirname自定义函数shel…...
考虑交叉耦合因素的IPMSM无传感器改进线性自抗扰控制策略
考虑交叉耦合因素的IPMSM无传感器改进线性自抗扰控制策略一级目录二级目录三级目录控制原理ELADRC信号提取龙格贝尔观测器方波注入simulink仿真给定转速:转速环:电流环:一级目录 二级目录 三级目录 首先声明一下,本篇博客是复现…...

2023年全国最新食品安全管理员精选真题及答案5
百分百题库提供食品安全管理员考试试题、食品安全员考试预测题、食品安全管理员考试真题、食品安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 41.《中华人民共和国食品安全法》第35条规定,以下࿰…...

git 笔记
简介 内容介绍 介绍git怎么管理和实现的 核心概念 文件名-hash-文件内容: 可以通过文件路径定位位置, 也可以通过hash定位位置;快照: 所谓一个快照其实就是一棵树, 叶子结点是一个hash,对应一个文件, 根节点对应文件夹; 一棵树就是一个快照;commit是tree, tree将文件串联, …...

ChatGPT 的盈利潜力:我使用语言模型赚取第一笔钱的个人旅程
使用 Fiverr、Python ChatGPT 和数据科学赚钱的指南。众所周知,ChatGPT 是 12 月发生的互联网突破性事件,几乎每个人都跳过了使用 AI 赚钱的潮流。在本文中,我将分享我是如何使用 ChatGPT 赚到第一笔钱的。本文包括以下主题:回到基…...

计算机网络——问答2023自用
1、高速缓冲存储器Cache的作用? 这种局部存储器介于CPU与主存储器DRAM之间,一般由高速SRAM构成,容量小但速度快,引入它是为了减小或消除CPU与内存之间的速度差异对系统性能带来的影响 (Cache可以保存CPU刚用过或循环使…...

【1247. 交换字符使得字符串相同】
来源:力扣(LeetCode) 描述: 有两个长度相同的字符串 s1 和 s2,且它们其中 只含有 字符 "x" 和 "y",你需要通过「交换字符」的方式使这两个字符串相同。 每次「交换字符」的时候&…...

【一天一门编程语言】Lisp 语言程序设计极简教程
Lisp 语言程序设计极简教程 Lisp 是一种古老的编程语言,它的特点是拥有很高的表示能力和灵活的可扩展性,拥有大量的现成函数库,同时也是一种动态类型的语言,十分适合用来实现大规模软件系统。本文介绍了 Lisp 程序设计的基本知识,帮助读者快速上手。 一、Lisp 简介 Lis…...

全后端交互数据加密
前后端交互 通信请求使用https对请求参数进行签名,防止数据篡改对请求参数以及响应数据进行加解密app中使用ssl pinning防止抓包操作 https协议 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-78n9M2PH-1677252127361)(安全.assets/ht…...
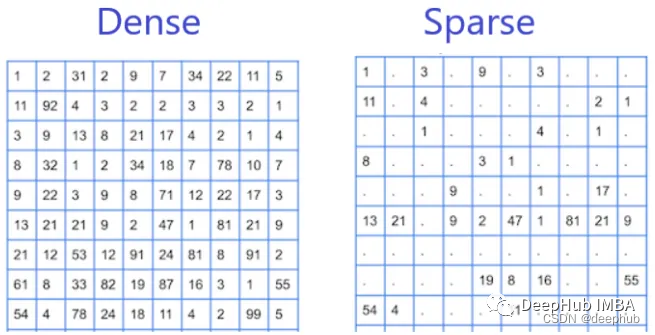
稀疏特征和密集特征
在机器学习中,特征是指对象、人或现象的可测量和可量化的属性或特征。特征可以大致分为两类:稀疏特征和密集特征。 稀疏特征 稀疏特征是那些在数据集中不连续出现的特征,并且大多数值为零。稀疏特征的示例包括文本文档中特定单词的存在或不存…...

Linux网络TCP sticky分析工具
1 TCP粘包 - TCP_NODELAY TCP粘包(sticky)的表现是TCP nagle算法将应用层发送的多个包进行合并后,再发送,很容易出现burst导致bcm89230丢包。由于OABR不支持流控,所以需要使用Linux tc对对应的TCP port进行流量整形。 …...

华为OD机试题,用 Java 解【DNA 序列】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

python的所有知识点+代码+注释,不看就亏死了
目录 简介 特点 搭建开发环境 版本 hello world 注释 文件类型 变量 常量 数据类型 运算符和表达式 控制语句 数组相关 函数相关 字符串相关 文件处理 对象和类,注:不是那个对象!!!!&…...
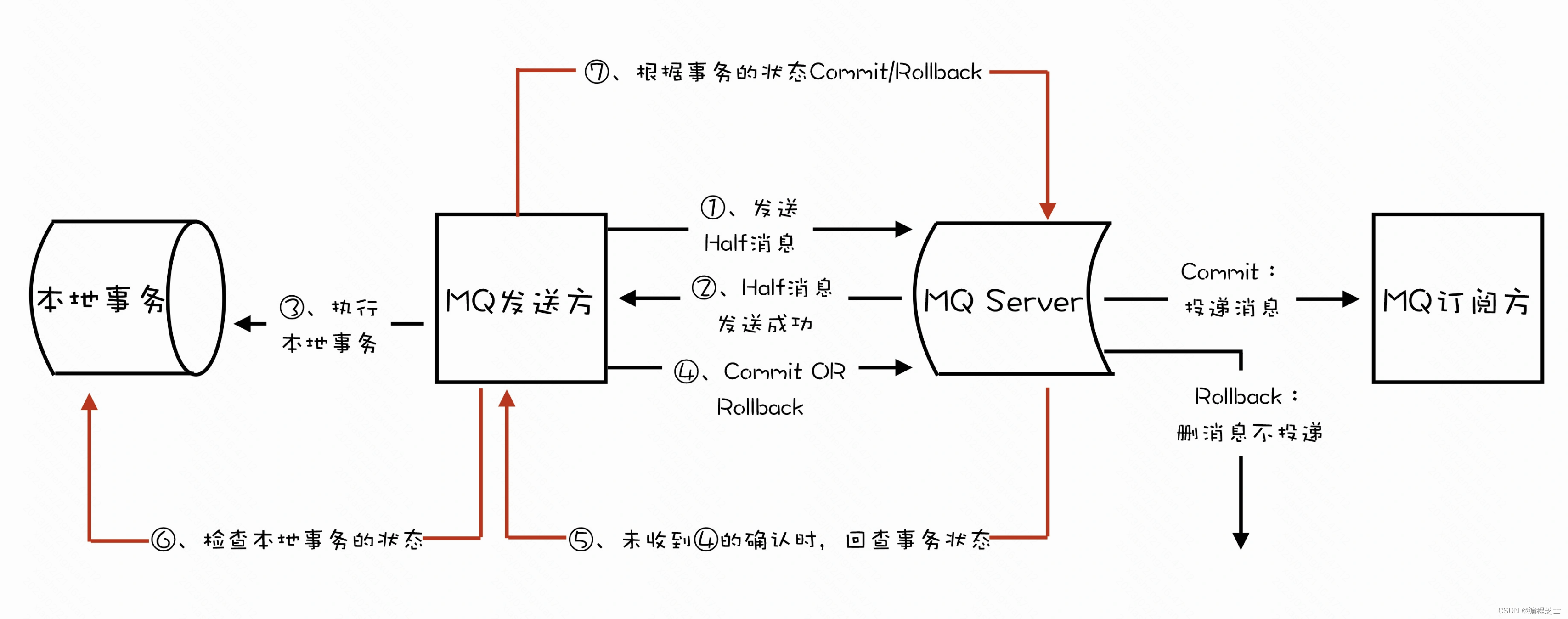
读懂分布式事务
一、概述 1.1 什么是分布式事务 事务我们都很熟悉,事务提供一种机制将一个活动涉及的所有操作纳入到一个不可分割的执行单元,组成这组操作的各个单元,要么全部成功,要么全部失败。 事务有四大特性: Atomic…...

多目标粒子群算法求解帕累托前沿Pareto,Pareto的原理,测试函数100种求解之21
目录 背影 parte前沿的定义 注意事项 基于多目标粒子群的帕累托前沿求解 主要参数 MATLAB代码 效果图 结果分析 展望 背影 在目标优化过程种,很多时候都两个或者多个目标,并且目标函数不能同时达到最优,鱼与熊掌不可兼得,这个时候可以通过求解帕累托前沿,通过帕累托前沿…...
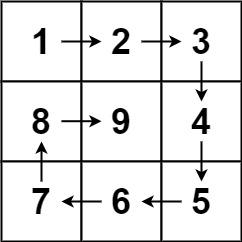
数组:二分查找、移除数组等经典数组题
二分查找:相关题目链接:https://leetcode.cn/problems/binary-search/题目重现:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值…...

负责任动物纤维标准RAF
【负责任动物纤维标准RAF】RAF-Responsible Animal Fiber, 中文翻译为负责任动物纤维标准。RAF标准包含了三个子标准,即RWS(责任羊毛标准)、RMS(责任马海毛标准)和RAS(责任羊驼毛标准)。RWS&…...
storybook使用info插件报错
报错内容: RangeErrorMaximum call stack size exceededCall StackprettyPrintvendors-node_modules_pmmmwh_react-refresh-webpack-plugin_lib_runtime_RefreshUtils_js-node_mod-4ff2dd.iframe.bundle.js:160:27undefinedvendors-node_modules_pmmmwh_react-refresh-webpack-…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
