二叉树,堆排序及TopK问题
要讲二叉树的概念,就要先讲树的概念。
树是什么呢?
树其实是一种储存数据的结构,因为他的结构倒过来和生活中的树很相似所以才被称之为树。
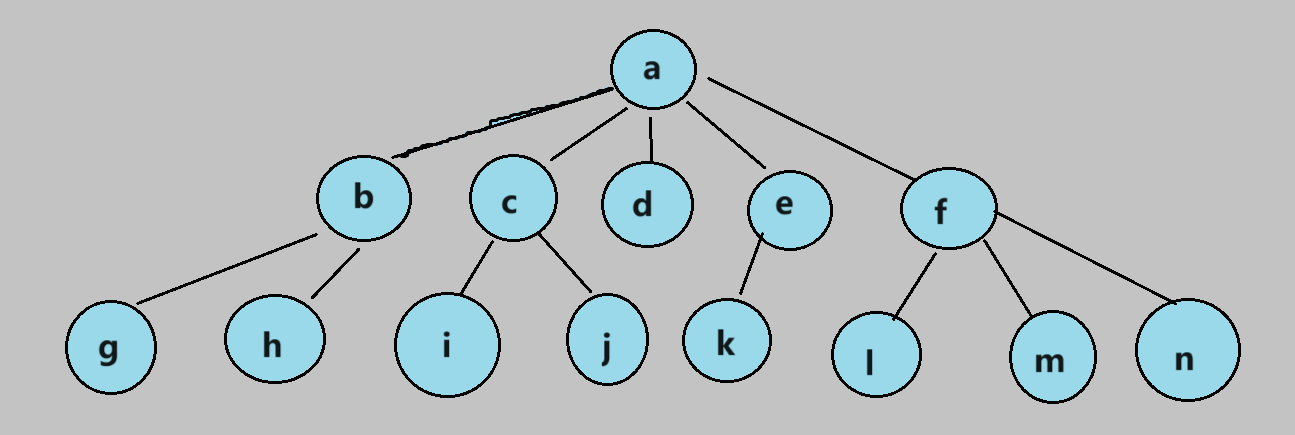
这是一颗多叉树,从最顶端的节点可以找到下边的几个节点,下边的节点又可以找到他的下一级节点,注意观察,如下边的g h i节点,他们返回上一级只有一条路径,从最上边找到他也只有唯一的路径。
树的结构之间不可以交叉,一个节点只能有一个爸爸节点,但是一个爸爸可以有多个孩子。
联想一下这个结构,是不是和我们windows下的文件夹很相似,一个文件夹打开后可以找到很多文件夹,从某个文件夹内找到另一个文件夹只有一条路径。
讲几个比较重要的概念。
节点的度:一个节点含有的子树的个数,即一个爸爸有几个孩子。
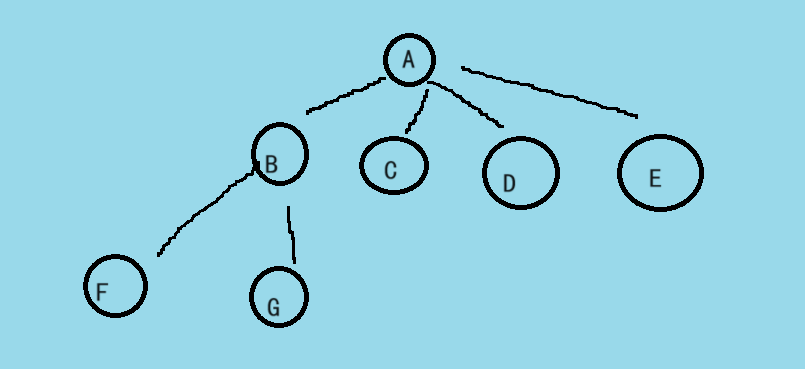
A的度为4,B的度为2。
树的度:一棵树里面所有节点中,最大的节点的度为树的度
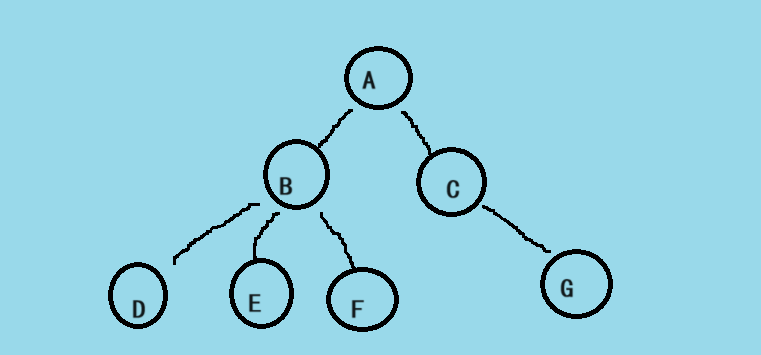
A的节点为2,B的节点为3,该树的度为3。
树的高度:就是树的深度
父节点:有孩子结点的节点,上图ABC都为父节点
子节点:上图除了A别的都可以称作子节点,他们都有父节点
节点的祖先:所有节点的祖宗,即A
兄弟节点:有相同的父节点的节点。F和G就不是相同的父节点,就不是兄弟节点。但是他们的爸爸在同一层,所以称为堂兄弟节点。、
多叉树的实现比较难搞,每个节点要保存父节点,还要保存他的兄弟节点,
所以我们先来实现一些简单的树形结构:二叉树。
二叉树
概念:这棵树的每个节点的子节点最多只能有两个,左孩子或者右孩子。
任意二叉树都由以下几种情况复合而成
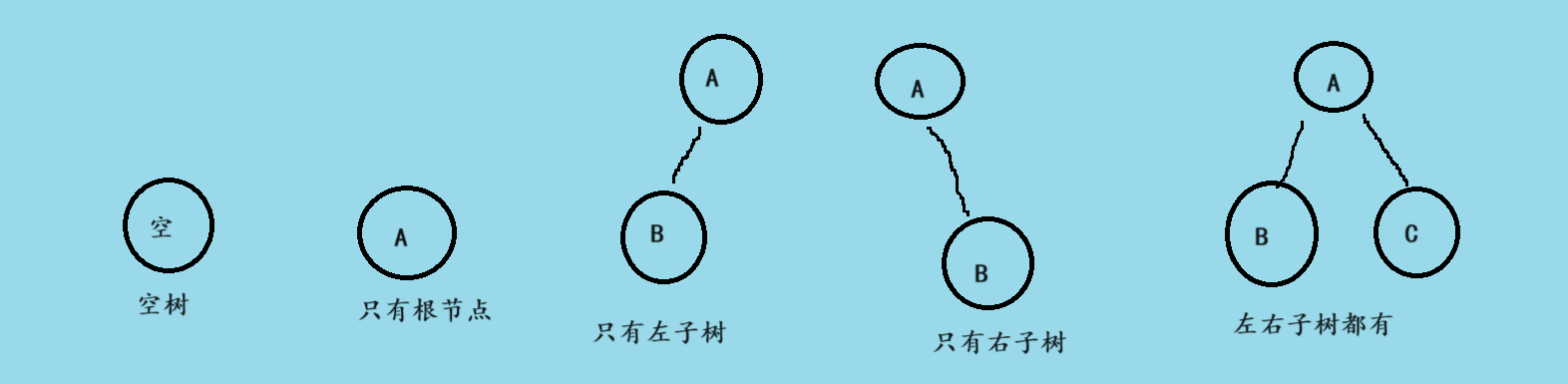
特殊的二叉树
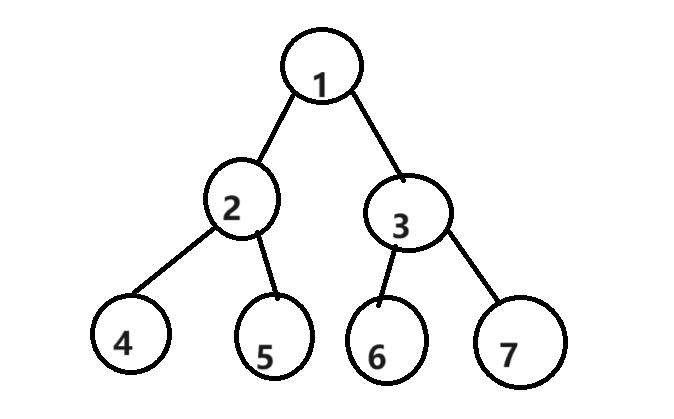
- 满二叉树:一个二叉树,如果他的每一层的节点数都达到最大值,这棵树就是满二叉树,如果该二叉树的层数为K,总结点个数为2k -1。
例如:

每个父亲节点都有两个孩子。
现实中的二叉树如图:


是不是超级标准。
2,完全二叉树
完全二叉树由满二叉树发展而来(满二叉树是完全二叉树的一种),如果一棵树有K个节点,这些节点从左往右依次数都是连着的,假设这里有一棵完全二叉树,节点个数为9。
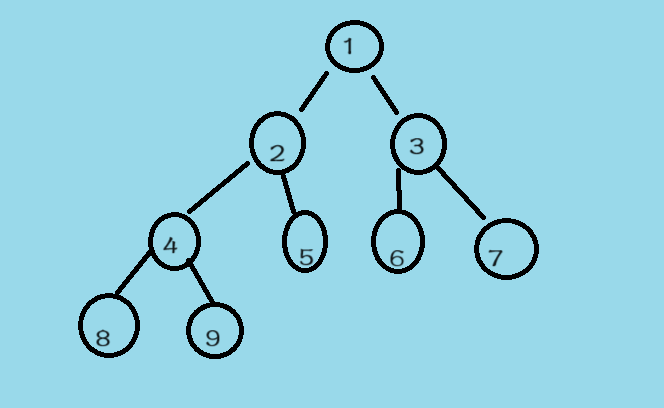
只能4有左孩子后才能有右孩子,同一层节点,如果左边的节点没有两个儿子,后边的节点都不能有孩子。
下边两棵树都不是完全二叉树。
二叉树的存储结构
1,顺序结构
顺序结构用数组来存储,但一般只适用于完全二叉树,完全二叉树使用数组存储的话不会因为有些地方是空的会造成空间的浪费,所以现实中只有用堆才会使用数组存储。
二叉树顺序存储在物理上是一个数组,在逻辑上是一棵完全二叉树。
第二种是链式储存,用链表表示一棵二叉树,这种结构在数据结构高阶中才会用到,我们不做仔细讲解。
普通二叉树是不适合用数组建堆的,会造成大量的空间浪费,但是完全二叉树不一样,他的节点是挨个建立的,我们接下来建堆就是用这种结构。
堆的概念
有一堆元素,以顺序表按照完全二叉树的顺序将其储存起来,堆有两种,大堆和小堆。
大堆
all父节点大于子节点,根节点的值最大,这样的堆叫做大堆
如果根节点最小,所有父节点的值小于子节点,那这个堆被称为小堆。
堆的创建
给一个数组,
a[5,6,2,8,9,4,7]
这个数组在逻辑上是一棵完全二叉树,但还不是一个堆。
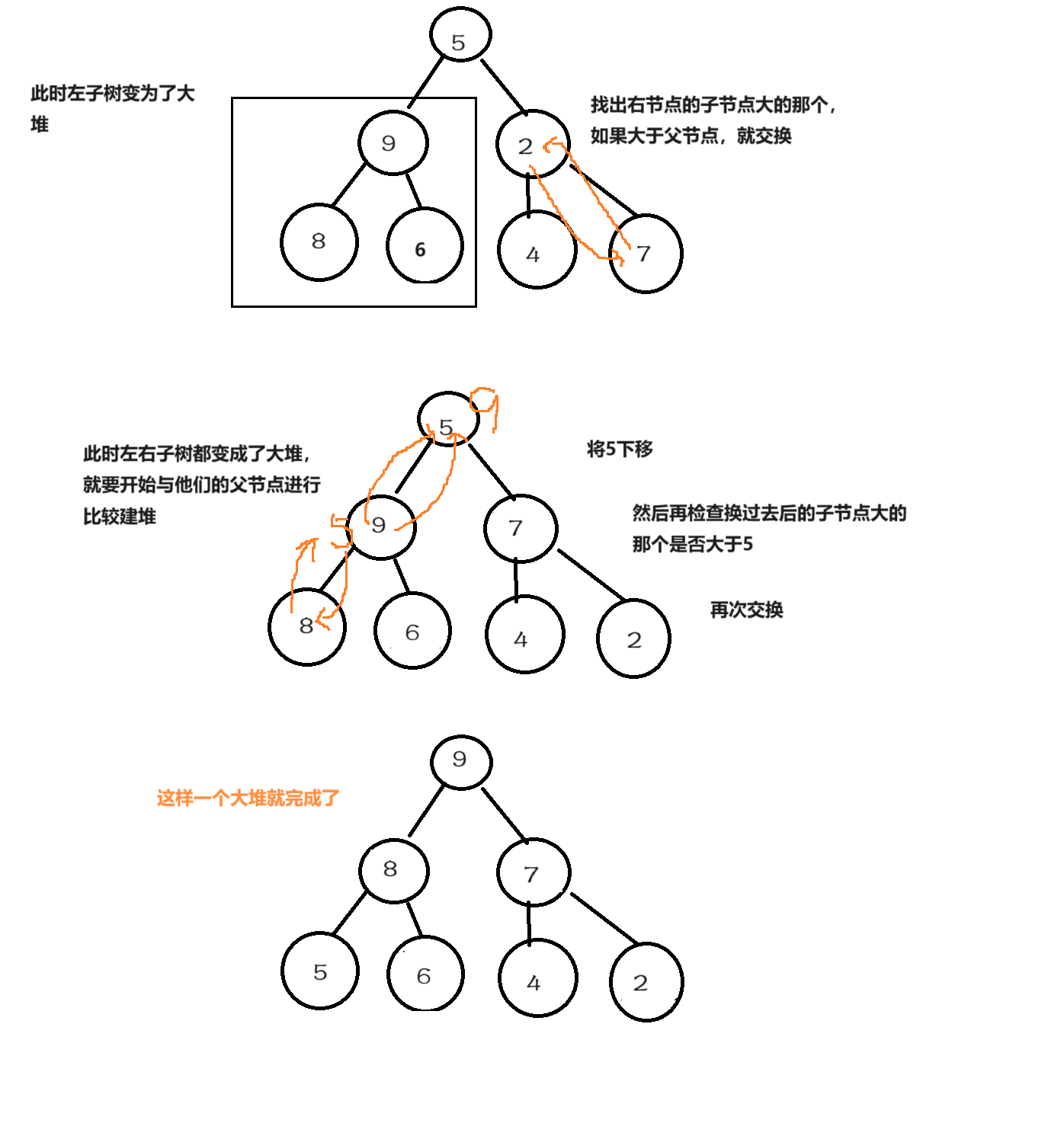
想要将它变成一个大堆,就要调整他的顺序。
首先我们会想到让根节点小于其子节点,然而其子节点也必须小于自己的子节点,所以想要让一棵树变为一个大堆,就要让自己的子树也变成一个大堆。
建堆过程如图
用数组的方式存储,但其逻辑上可以看作是一棵二叉树,完全二叉树
这里的1,2,3,4,5,6,7是数组的下标,
可以发现,若知道一个子节点的下标为child,其父节点的下标为(child-1)/2。
知道一个父节点parent,其左孩子节点的下标为parent2+1。右孩子的下标为parent2+2。
建堆的时间复杂度
向下调整法
向下调整法通过父节点的下标找左右孩子,不断判断值的大小,交换建堆。
代码如下
//向下调整
void AdjustDown(HeapStyle* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){//找出小的孩子if (child + 1 < n && a[child]> a[child + 1]){++child;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
为了容易计算,且满二叉树是完全二叉树的一种,为了化简过程就利用满二叉树来证明。
假设树的高度为n
第一层一个节点最多需要向下调整n-1层
第二层21个节点,最多每个节点要调整h-2层
第三层有22个节点,最多每个节点要调整h-3层
…
第h-1层2h-2个节点,最多向下调整一层

建堆的时间复杂度为O(N)。
向上调整法建堆
第一层不需要调整
第二层21个节点,每个节点最多需要向上调整1次。
第三层22个节点,每个节点最多向上调整2次
…
第h-1层2h-2个节点,最多每个节点向上调整h-2次。
第h层2h-1个节点,每个节点最多向上调整h-1次。
不用算就可以得出向上调整的时间复杂度为O(N2)。
向上调整法通过孩子找父亲判断交换建堆
代码如下
//向上调整
void AdjustUp(HeapStyle* a, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
建堆过程
通过上边的分析,我们已经知道向下调整法相对于向上调整优势巨大,所以在建堆的过程中,使用向下调整法,遍历数组的每个节点,使用向下调整法建大堆,上边的流程图可知如果从根节点开始建堆,不能确保左子树和右子树是否为堆,最后一层不需要调整,从倒数第二层开始调整,使其变为一个堆。
//找出小的孩子if (child + 1 < n && a[child]> a[child + 1]){++child;}
找出该节点左右孩子中大的那个。
if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}
如果小于,就互换,越小越往上,所以建的是小堆,将判断条件更改为大于号,即建大堆。这里的大于号和小于号是建大堆还是建小堆的关键。
利用循环,交换后将parent改为child,child也更新一次,是因为更换过来的父节点有可能比该子树的子节点更小。
如图所示
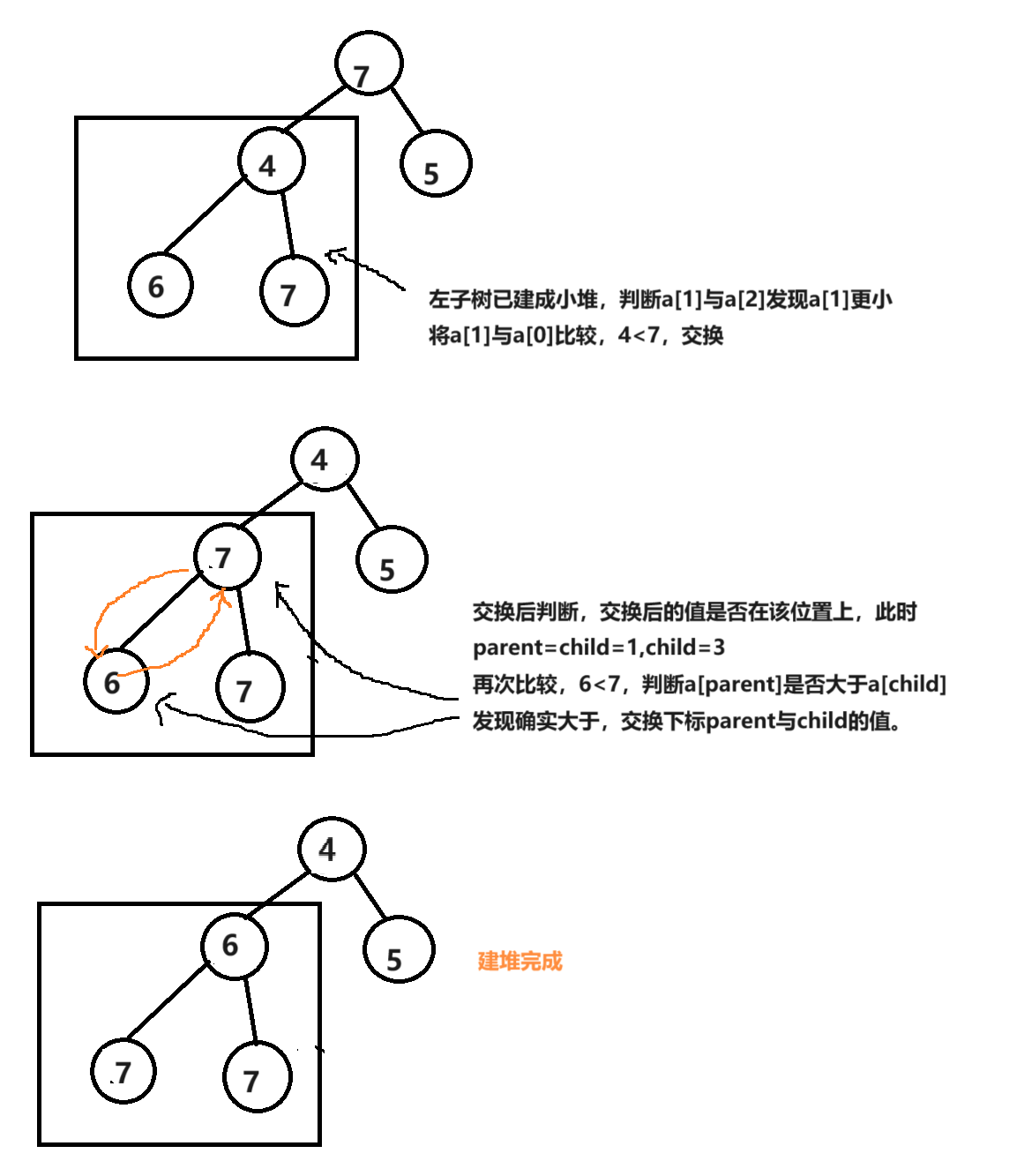
给定一个数组a[k]
for (int i = (k - 2) / 2; i >= 0; --i)//这里要思考一下{AdjustDown(minheap, k, i);}
从倒数第二层开始建堆即可,k-1是数组最后一个函数,要想知道其父节点下标,要减一再除以2,所以就变成了(k-2)/2。
堆排序
假设我们要排升序
建立一个大堆,堆顶元素一定是最大的那个,如果直接取出根节点,那么我们建的堆将被破坏,左子树和右子树可能就不再是大堆。
就像上图数组,建堆后下标为0,1,2,3,4的数字为4 6 5 7 7,如果取出4,剩余的6,5,7,7明显不再是一个堆,我们又要重新建堆,这样堆排序有什么优势可言,时间复杂度就变为O(N2)。如何取出根节点又不破坏左子树和右子树的大堆状态呢?
将堆顶元素与最后一个交换,最大的数就到了数组最后边,然后只需要对换过去的根节点向下调整即可。
代码如下
//向下调整
void AdjustDown(HeapStyle* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){//找出小的孩子if (child + 1 < n && a[child]< a[child + 1])//找出左右子树大的那个{++child;}if (a[child] > a[parent])//建大堆,大于就交换{swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void Heapsort(int* a, int n)//建大堆
{for (int i = (n-2)/2; i >=0; i--){AdjustDown(a,n, i);}//int end = n - 1;while (end > 0){swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}
int end=n-1。a[end]为最后一个节点,交换后传参为n-1,向下调整就不再带最后一个节点玩了,直到调整至第一个节点,这样这个数组就有序了。
TOPK问题
TOPK问题在生活中常常出现,就比如年级前几名,饭店味道排名等等等等,如何在一大地数据中找到前几名呢?
如果我们建一个小堆,那么堆顶节点即为整棵树最小的那个,假设有10000个数据,我们要找出其中的前10个,我们就可以使用前十个元素建一个小堆,然后再让剩下的元素与堆顶元素进行比较,如果大于对顶元素,就与对顶元素进行交换,然后向下调整重新建出一个小堆,这时堆顶元素会发生变化,会变成一个新的堆中最小的数,遍历完成之后队中剩下的元素即为这10000个数里面最小的那个。
创建一个数组向里面写入10000个随机数进行测试。
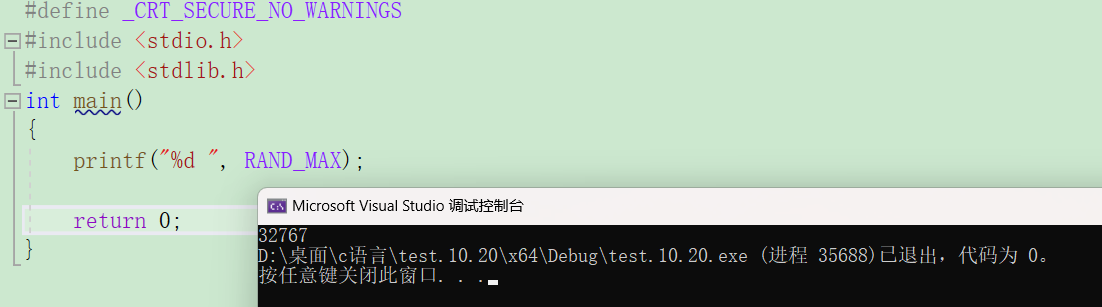
随机数的范围是32767,如果我们创建100000个数据,只会出现很多重复的数据,所以我们就使用一万个数据测试一下数据。
代码如下
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
//int main()
//{
// printf("%d ", RAND_MAX);
//
// return 0;
//}void swap(int* a, int* b)
{int swp = 0;swp = *a;*a = *b;*b = swp;
}
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//找出小的孩子if (child + 1 < n && a[child] > a[child + 1]){++child;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void TestTopk()
{int n = 10000;int* a = (int*)malloc(sizeof(int) * (n));srand(time(0));for (int i = 0; i < n; i++){a[i] = rand() % 10000;}a[5] = 100000 + 1;a[6100] = 100002;a[1007] = 100003;a[8678] = 888888;a[3459] = 777777;int k = 10;for (int i = (k - 2) / 2; i >= 0; i--)//倒数第二层最后一个节点{AdjustDown(a, k, i);//传入下标}//以前k个数建堆完毕for (int i = k + 1; i < n; i++){if (a[i] > a[0]){swap(&a[i], &a[0]);}AdjustDown(a, k, 0);}for (int i = 0; i < k; i++){printf("%d ", a[i]);}
}int main()
{TestTopk();return 0;
}
为了测试方便,我们修改了数组中的几个数值。
运行后如下
是不是小堆呢?
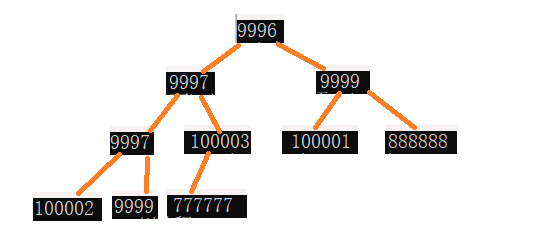
答案是,他就是个小堆,这样一万个数据里的前10个最大的数据就找出来了。
然而10000个数据是不是有点太少了。
我们普通创建的数组存储在栈上,malloc出的数组存放在堆里,如果有很多很多数据,就会占据很多时间,我们可以考虑将这些数字存放在一个文件里,然后利用相关的文件操作找出这些数字里最大得前几个。
向文件里写入数据
//创造数据
void CreatNData()
{int n = 1000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen,error");return;}for (int i = 0; i < n; ++i){int x = rand() % 100000;//然而最大不过32767,有很多重复数据得了fprintf(fin, "%d\n", x);}int k = 10;//PrintTopk(file, k);fclose(fin);
}
创建完成之后可以打开修改修改数据,然后在main函数里将创建数据的函数注释,防止数据覆盖。
打开后直接就是一顿修改
那几个后边数字相同且贼大的就是修改的数据。
void PrintTopk(const char*file, int k)
{//1,建堆--用a中的前k个元素建堆FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);//依次先读K个数}for (int i = (k - 2) / 2; i >= 0; --i)//这里要思考一下{AdjustDown(minheap, k, i);}//2.将剩余的n-k个元素依次与堆顶元素int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){//替换进堆minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}fclose(fout);
}
逻辑和上边malloc出的数组找最大得前十个一样。建小堆,找到小于根节点的数据就进行交换,交换后再次进行向下调整。
要注意,rand出的数据最大32767,因为我们创建了一百万个数据,所以如果不修改数据的话,查找出来的都会是32767。
运行结果如图
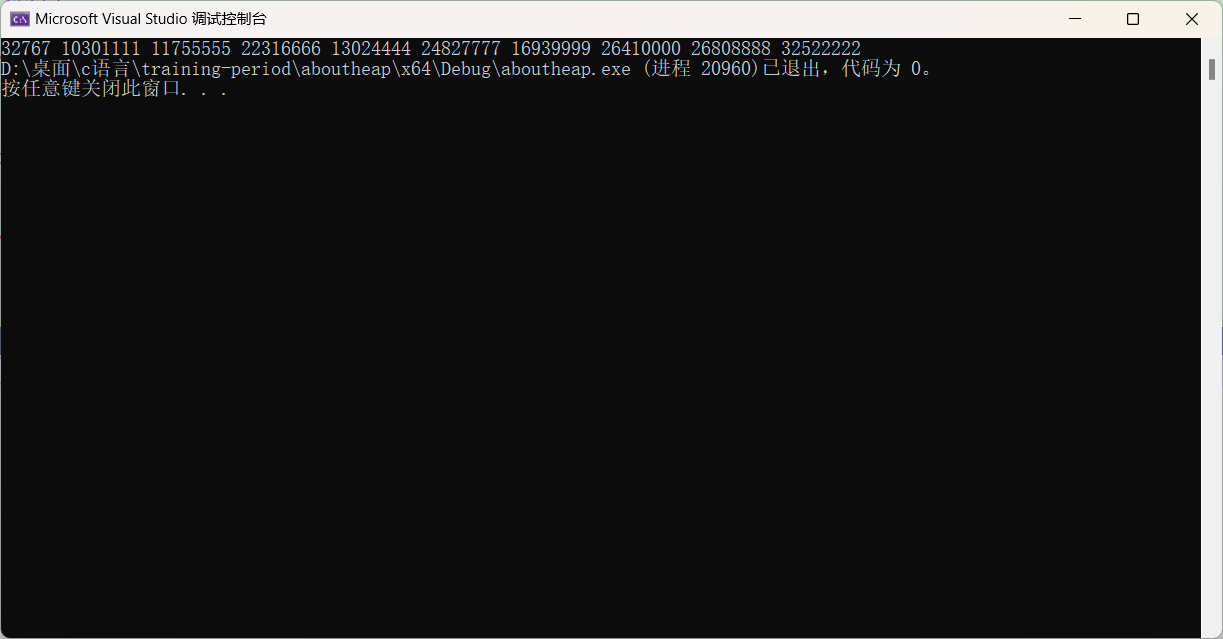
是一个小堆
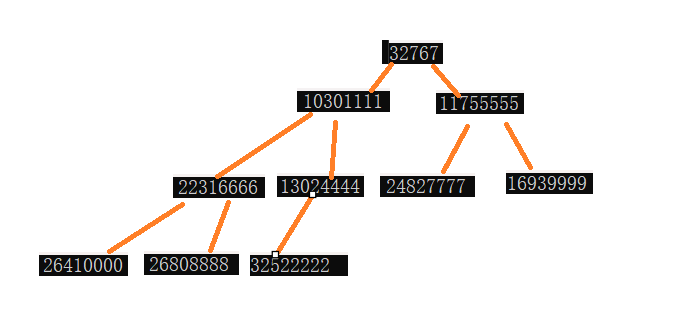
对顶元素在预料之中。这样Topk问题就解决啦。
这篇文章就讲解到这里,如果有什么问题欢迎大家提出指正。
相关文章:

二叉树,堆排序及TopK问题
要讲二叉树的概念,就要先讲树的概念。 树是什么呢? 树其实是一种储存数据的结构,因为他的结构倒过来和生活中的树很相似所以才被称之为树。 这是一颗多叉树,从最顶端的节点可以找到下边的几个节点,下边的节点又可以找…...

iphone xr密码错误太多次 连接itunes
itunes下载的固件在电脑在电脑的“C:\Users\用户名\AppData\Roaming\Apple Computer\iTunes\iPhone Software Updates”文件夹之中。 如果你忘记了 iPhone 密码 - 官方 Apple 支持 (中国) 下载和使用 Windows 10 版 iTunes - 官方 Apple 支持 (中国) 查找手机 iClo…...

设置RabbitMQ超时时间
RabbitMQ默认的超时时间是30分钟,在消息消费超过30分钟后,rabbitMQ会发生错误,导致整个channel被销毁,无法继续消费 在RabbitMQ安装的终端执行 rabbitmqctl eval application:set_env(rabbit,consumer_timeout,180000000). 命令…...
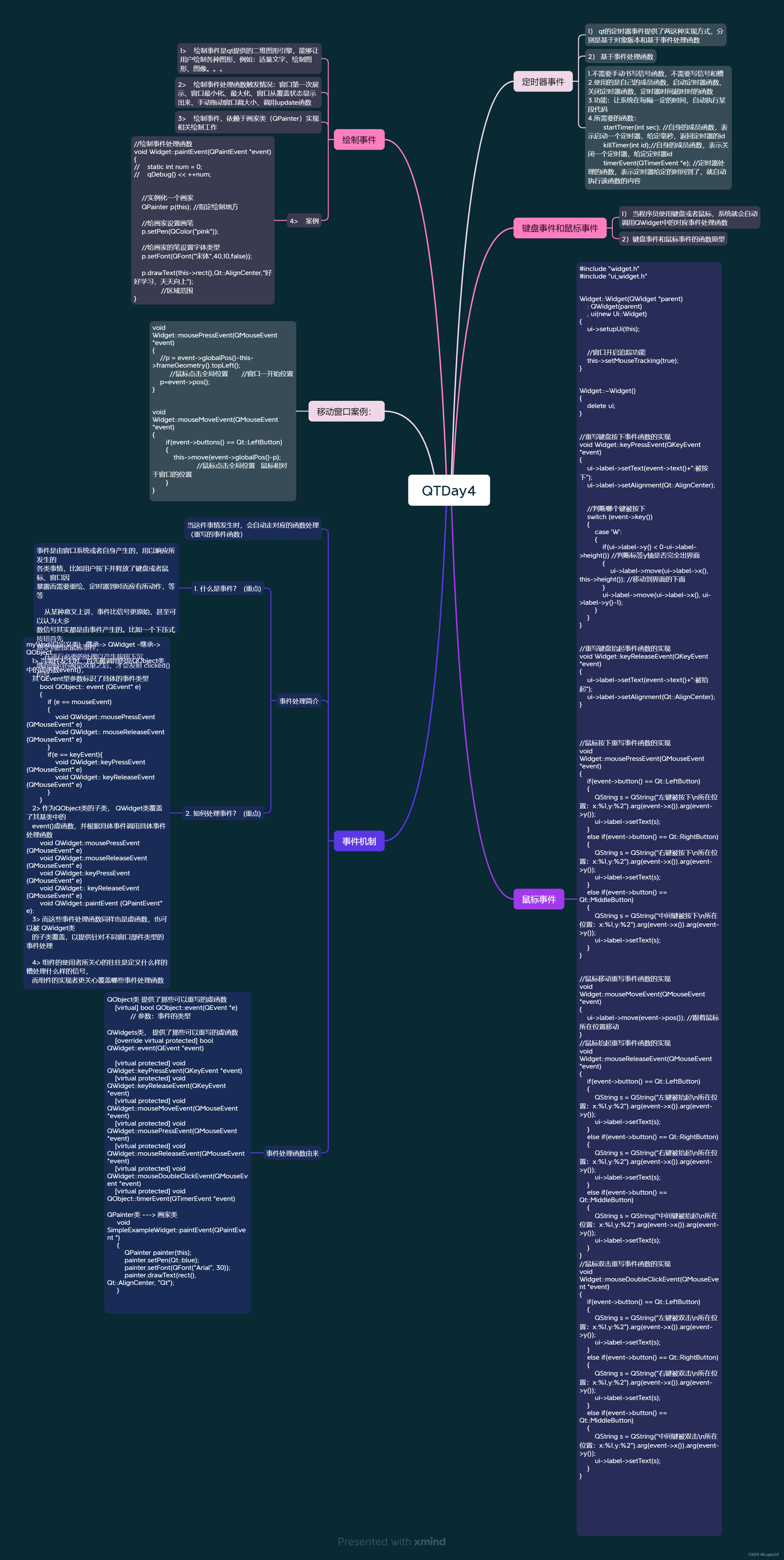
QT计时器
widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTimerEvent> //计时器类 #include <QTime> //时间类 QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widg…...
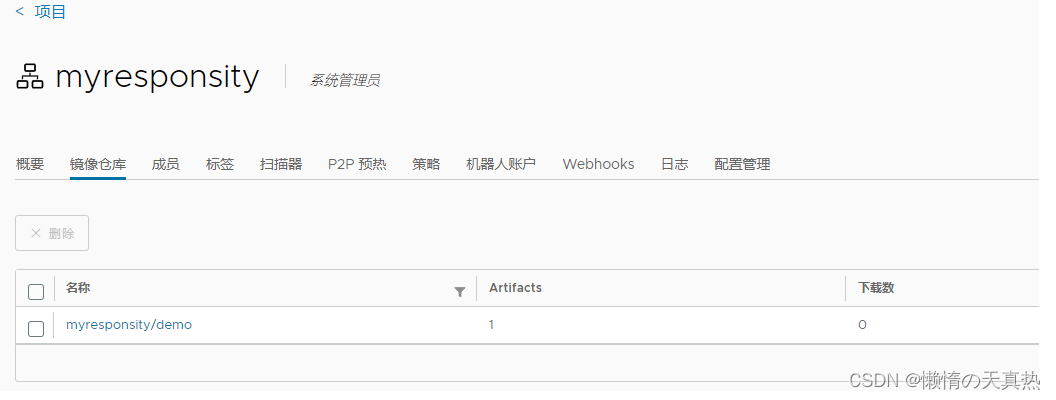
3-k8s-镜像仓库harbor搭建
文章目录 一、概念二、安装harbor三、使用harbor仓库 一、概念 官方概念:Harbor是一个用于存储和分发Docker镜像的企业级Registry服务器。 我们平时拉去镜像都是从线上仓库拉去,但是企业内部的镜像一般都不会随意传到网上,而是保存在自己公…...
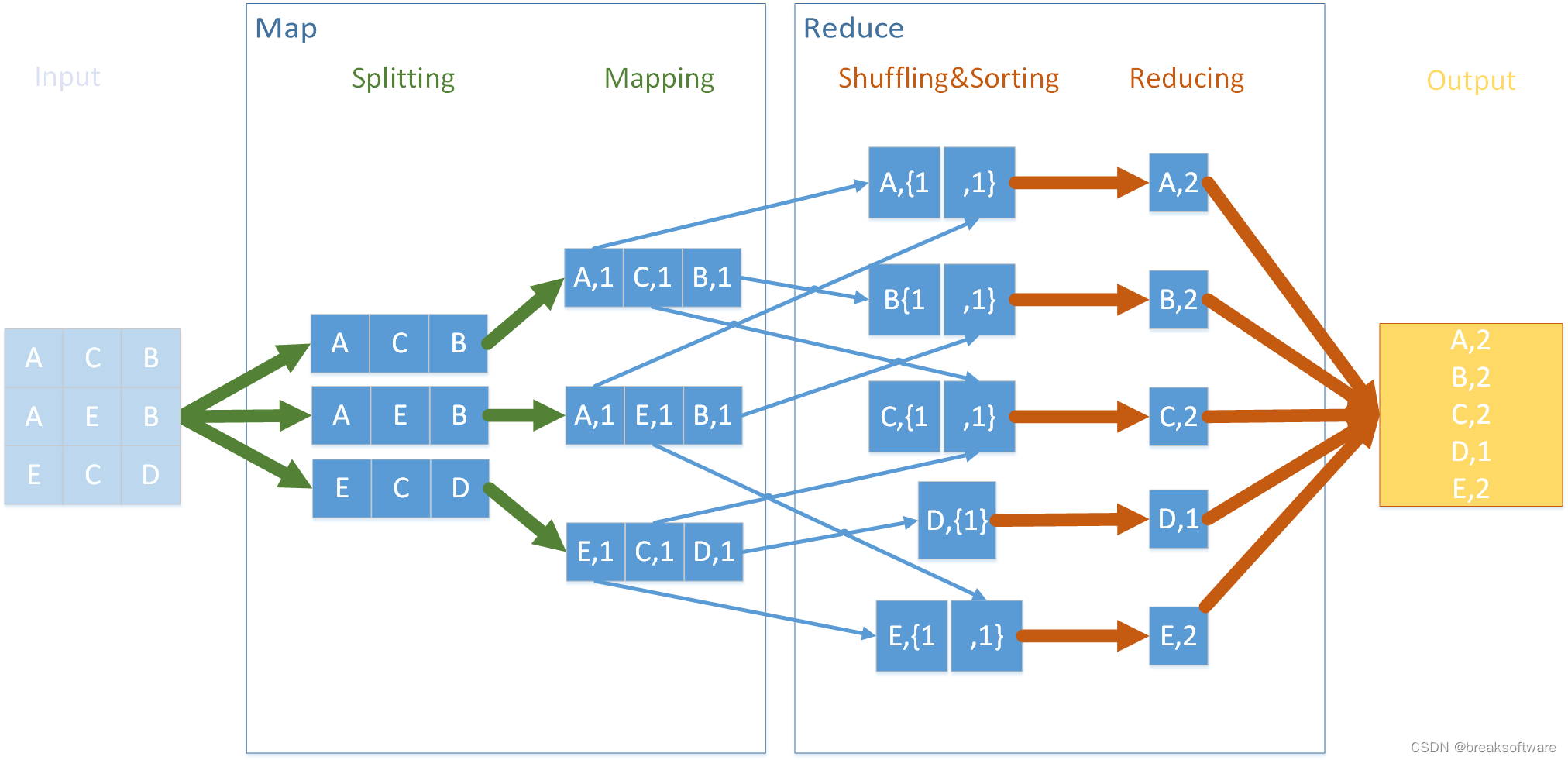
0基础学习PyFlink——模拟Hadoop流程
学习大数据还是绕不开始祖级别的技术hadoop。我们不用了解其太多,只要理解其大体流程,然后用python代码模拟主要流程来熟悉其思想。 还是以单词统计为例,如果使用hadoop流程实现,则如下图。 为什么要搞这么复杂呢? 顾…...
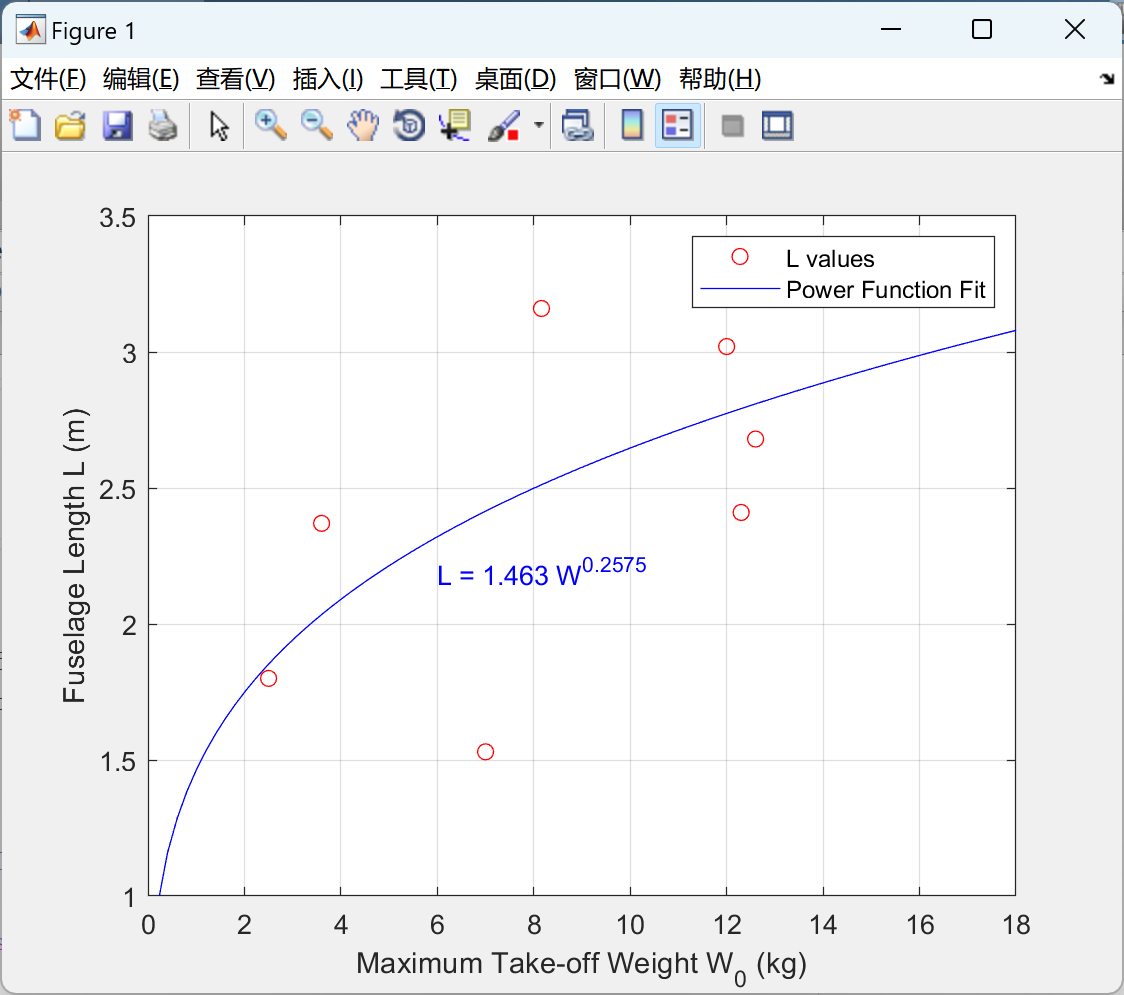
【无人机】太阳能伪卫星VoLTE无人机设计(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

2023.10.20 LED驱动
驱动程序 #include<linux/init.h> #include<linux/module.h> #include<linux/fs.h> #include<linux/uaccess.h> #include<linux/io.h> #include"head.h"unsigned int major; unsigned int *vir_moder; unsigned int *vir_odr; unsign…...

【力扣刷题】回文链表、环形链表、合并两个有序链表
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 刷题篇 一、回文链表1.1 题目描述1.2 思路分…...

linux错误处理函数
linux c之perror、exit_perror与exit-CSDN博客 linux网络编程(三) TCP通信时序与多进程/线程并发服务器的编写-阿里云开发者社区 函数简介篇——错误处理函数:errno值、perror()、streeor()、streeor_r()_惺忪牛犊子的博客-CSDN博客...
-条件渲染和列表渲染)
vue2技能树(5)-条件渲染和列表渲染
目录 Vue 2 条件渲染详解v-if 和 v-else 指令项目示例 v-show 指令项目示例 v-if 和 v-show 的区别v-if 和 v-else-if 指令项目示例 Vue 2 列表渲染详解v-for 指令项目示例 计算属性和方法项目示例 v-bind:key项目示例 使用对象的v-for项目示例 v-for 的索引项目示例 …...

MySQL基本操作之创建数据库
1、大小写敏感 一般大家都默认使用:小写 在MySQL中,大小写敏感性有两个方面的规定:lower_case_file_system和lower_case_table_names。 lower_case_file_system:指定操作系统文件系统是否对大小写敏感。 当设置为ON时,表示文件系统对大小写不敏感;当设置为OFF时,表示…...
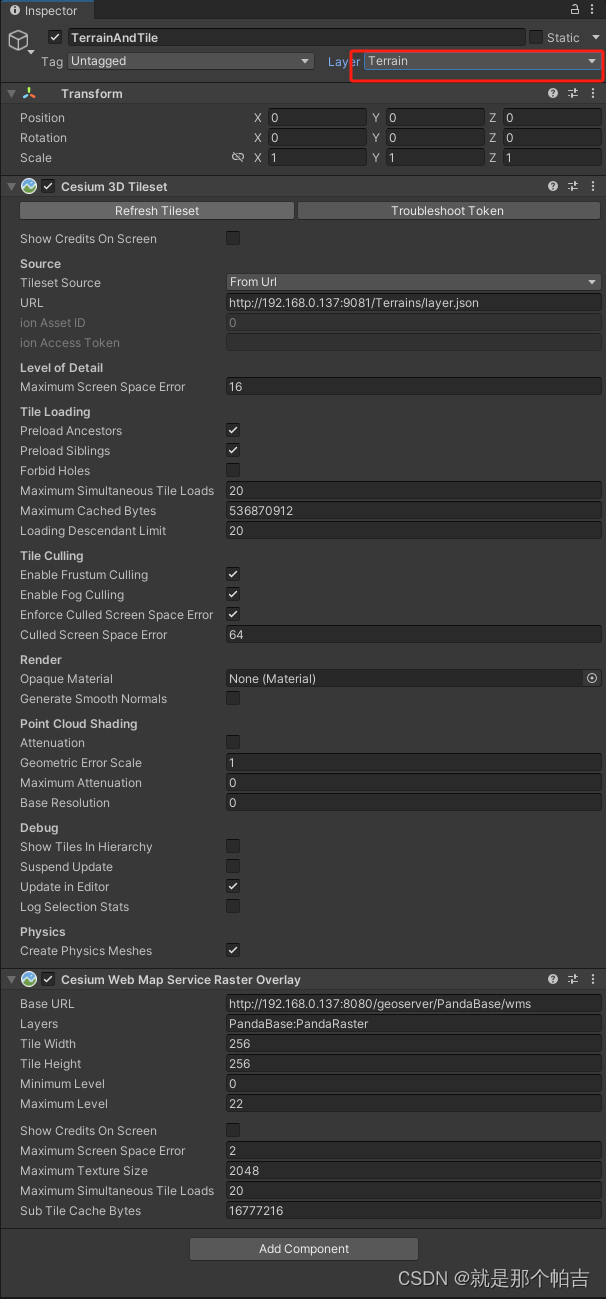
8.对象贴地
愿你出走半生,归来仍是少年! 在场景中,有时候需要对地物(房屋、楼宇)进行贴地处理,或者说相对地面高度(井盖、井室)进行设置。 通过自定义的Terrain切片以及影像瓦片构建的三维场景应该如何获取…...
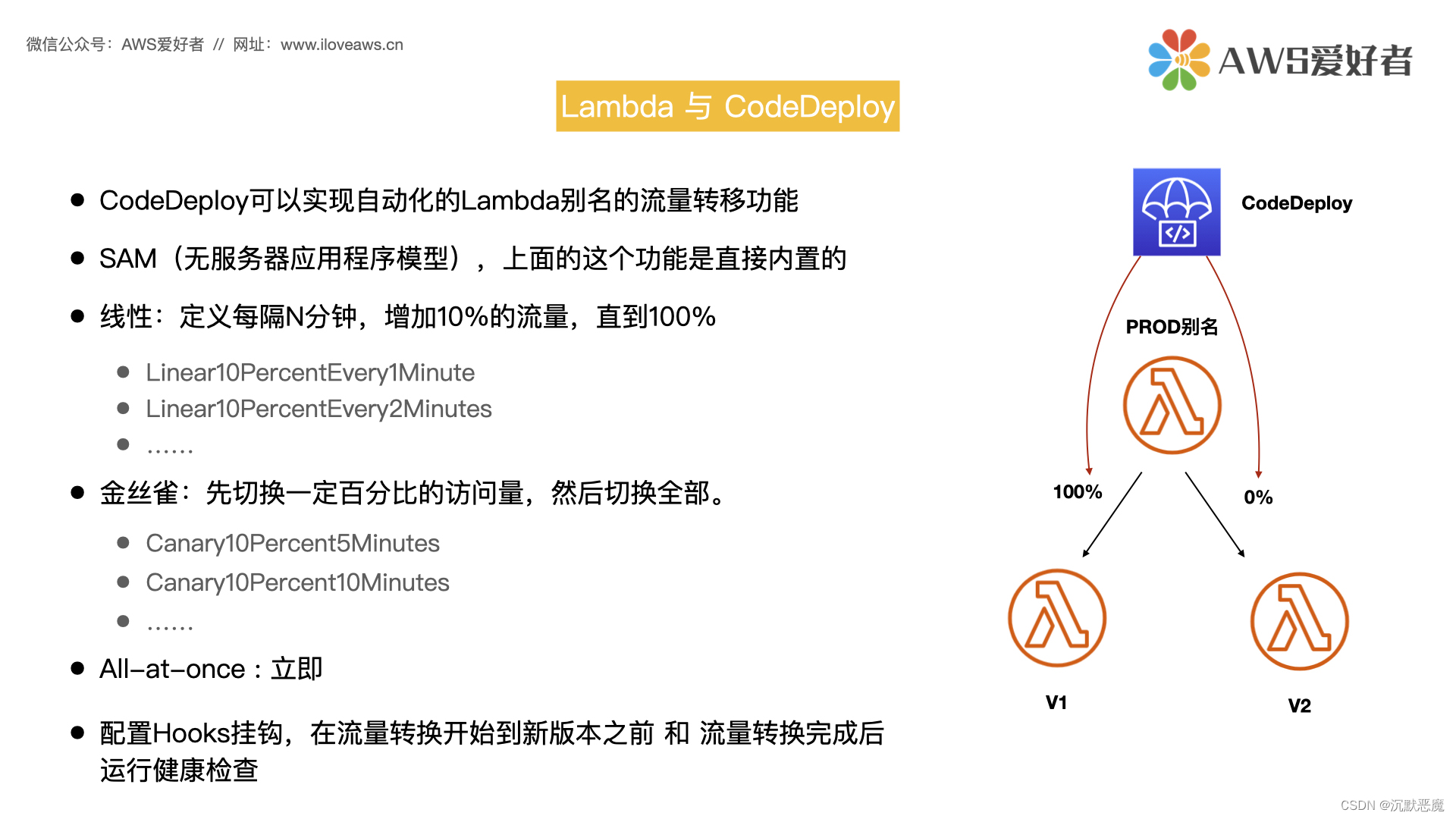
AWS Lambda – 函数版本,别名,API网关,CodeDeploy协同
Hello大家好,我们今天继续讨论AWS Lambda的内容。 Lambda函数的版本 Lambda函数的版本和别名是辅助资源,我们可以通过创建这些资源管理函数的部署和调用。 首先,让我们来看一下Lambda 函数版本的概念。您可以使用版本来管理函数的部署。例…...

flutter doctor检测环境,出现CocoaPods installed but not working
1. 安装flutter, 地址: 安装和环境配置 - Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 2. 安装成功后,通过flutter doctor检测环境。以mac为例,出现了CocoaPods installed but not working 错误提示时,以下为解决方案: 2.1 rvm i…...

Python 条件和 if 语句
Python支持来自数学的通常逻辑条件: 等于:a b不等于:a ! b小于:a < b小于或等于:a < b大于:a > b大于或等于:a > b 这些条件可以以多种方式使用,最常见的是在"i…...
行业领先的三个企业正在利用聊天机器人变得更强
聊天机器人已成为客户服务领域的革命者,深刻地改变了企业与客户互动的方式。这些虚拟助手简化了交互,提供了24/7全天候高效和个性化的支持。凭借先进的技术和自然语言处理能力,聊天机器人擅长快速处理查询。 效率是聊天机器人的关键优势。它…...

「Git|场景案例」从项目中删除之前commit过的文件并且让git不追踪删除操作
本文主要介绍如何在git中删除文件但是让git不追踪这些删除操作 文章目录 场景说明解决方案删除一个文件删除一个文件夹以及子文件夹 场景说明 自己在使用react开发一个包含大量媒体文件的网站时,项目初期临时将这些媒体文件都放在项目中,直接使用访问本…...
一款.NET Core开源的基于Vue+ElementUI开发的博客系统 - StarBlog
前言 今天给大家推荐一款.NET Core开源的基于VueElementUI开发的博客系统 - StarBlog。该项目配套详细的文章教程,可以作为 .Net Core 入门项目学习。 官方项目介绍 StarBlog支持Markdown导入的博客。后端基于最新的.Net6和Asp.Net Core框架,遵循REST…...

用git stash暂存修改
git stash命令用于保存当前工作目录的临时状态,包括暂存区和已修改但未暂存的文件。它会将这些修改保存在一个临时区域(即“堆栈”)中,让你能够回到一个干净的工作目录,可以进行其他操作。等到你完成其他任务后&#x…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
高抗扰度汽车光耦合器的特性
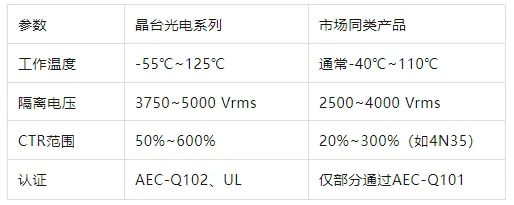
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
