【C语言必知必会 | 子系列第六篇】深入剖析循环结构(2)
引言
C语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发。它在编程语言中具有举足轻重的地位。
此文为【C语言必知必会】第六篇,基于进行C语言循环结构的编程题专项练习,结合专题优质题目,带领读者从0开始,深度掌握知识点。

文章目录
- 1️⃣ 前言
- 2️⃣PTA专项练习
- 7-1 统计一行字符中各类字符的个数
- 7-2 打印九九口诀表
- 7-3 二分法求多项式单根
- 7-4 梅森数
- 7-5 单词长度
- 7-6 21循环-求和3
- 7-7 21循环-金字塔
- 3️⃣ 总结
1️⃣ 前言
在【C语言必知必会】系列中,我们学习了顺序结构、选择结构、循环结构等,同时也通过专项练习进行了知识点的巩固和手敲代码的锻炼。
在子系列中,我们将基于PTA教学平台,向C语言学习者提供更优质的题目与更巧妙、精髓的解题思想与方法。
PTA是一个程序设计类实验辅助教学平台,由千名老师共同建设,里面包含了上万道高质量题目,用户量达百万。
在本讲中,将深入讲解循环结构编程题,在思想上引领读者,带领读者在理论结合实际的基础上更好地学习、吸收、掌握C语言。
2️⃣PTA专项练习
接下来,开始我们的循环结构专篇练习。
7-1 统计一行字符中各类字符的个数
用户输入一行字符(以回车符作为结束),请统计这行字符中,大小写字母个数、数字字符个数、空格个数和其它字符个数。
输入格式:
一行字符,以回车符作为结束。
输出格式:
输出4个以空格作为间隔的整数,分别代表大小写字母个数、数字字符个数、空格个数和其它字符的个数。
输入样例:
Tersfi23&* sdf A$
输出样例:
10 2 4 3
解题思路:
使用while语句结合getchar函数来匹配回车符
代码如下:
#include <stdio.h>
int main()
{int zimu=0,shuzi=0,space=0,other=0;char c;while((c=getchar())!='\n'){if((c>='a'&&c<='z')||(c>='A'&&c<='Z')){zimu++;}else if(c>='0'&&c<='9'){shuzi++;}else if(c==' '){space++;}else{other++;}}printf("%d %d %d %d",zimu,shuzi,space,other);}
7-2 打印九九口诀表
下面是一个完整的下三角九九口诀表:
1*1=1
1*2=2 2*2=4
1*3=3 2*3=6 3*3=9
1*4=4 2*4=8 3*4=12 4*4=16
1*5=5 2*5=10 3*5=15 4*5=20 5*5=25
1*6=6 2*6=12 3*6=18 4*6=24 5*6=30 6*6=36
1*7=7 2*7=14 3*7=21 4*7=28 5*7=35 6*7=42 7*7=49
1*8=8 2*8=16 3*8=24 4*8=32 5*8=40 6*8=48 7*8=56 8*8=64
1*9=9 2*9=18 3*9=27 4*9=36 5*9=45 6*9=54 7*9=63 8*9=72 9*9=81
本题要求对任意给定的一位正整数N,输出从1*1到N*N的部分口诀表。
输入格式:
输入在一行中给出一个正整数N(1≤N≤9)。
输出格式:
输出下三角N*N部分口诀表,其中等号右边数字占4位、左对齐。
输入样例:
4
输出样例:
1*1=1
1*2=2 2*2=4
1*3=3 2*3=6 3*3=9
1*4=4 2*4=8 3*4=12 4*4=16
解题思路:
-
使用for循环嵌套
-
当两个乘数相等时换行
代码如下:
#include <stdio.h>
int main()
{int i,j;int n;scanf("%d",&n);for(i=1;i<=n;i++){for(j=1;j<=i;j++){printf("%d*%d=%4d",j,i,j*i);if(i==j){printf("\n");}}}
}注意:
- 表示左对齐,而 4 表示占据4位宽度
右对齐直接%4d就行
7-3 二分法求多项式单根
二分法求函数根的原理为:如果连续函数f(x)在区间[a,b]的两个端点取值异号,即f(a)f(b)<0,则它在这个区间内至少存在1个根r,即f®=0。
二分法的步骤为:
- 检查区间长度,如果小于给定阈值,则停止,输出区间中点(a+b)/2;否则
- 如果f(a)f(b)<0,则计算中点的值f((a+b)/2);
- 如果f((a+b)/2)正好为0,则(a+b)/2就是要求的根;否则
- 如果f((a+b)/2)与f(a)同号,则说明根在区间[(a+b)/2,b],令a=(a+b)/2,重复循环;
- 如果f((a+b)/2)与f(b)同号,则说明根在区间[a,(a+b)/2],令b=(a+b)/2,重复循环。
本题目要求编写程序,计算给定3阶多项式f(x)=a3*x^3+a2*x^2+a1*x+a0在给定区间[a,b]内的根。
输入格式:
输入在第1行中顺序给出多项式的4个系数a3、a2、a1、a0,在第2行中顺序给出区间端点a和b。题目保证多项式在给定区间内存在唯一单根。
输出格式:
在一行中输出该多项式在该区间内的根,精确到小数点后2位。
输入样例:
3 -1 -3 1
-0.5 0.5
输出样例:
0.33
解题思路:
按照题目要求构建代码即可
代码如下:
#include<stdio.h>int main()
{double a0,a1,a2,a3,a,b;scanf("%lf %lf %lf %lf %lf %lf",&a3,&a2,&a1,&a0,&a,&b);while((b-a)>0.01){double s=(a+b)/2;double fs=a3*s*s*s+a2*s*s+a1*s+a0;double fa=a3*a*a*a+a2*a*a+a1*a+a0;double fb=a3*b*b*b+a2*b*b+a1*b+a0;if(fs==0){printf("%lf",s);}if(fa*fb<=0){if(fs/fa>0)a=s;elseb=s;}}printf("%.2lf",(a+b)/2);return 0;
}
7-4 梅森数
形如2n−1的素数称为梅森数(Mersenne Number)。例如22−1=3、23−1=7都是梅森数。1722年,双目失明的瑞士数学大师欧拉证明了2^31−1=2147483647是一个素数,堪称当时世界上“已知最大素数”的一个记录。
本题要求编写程序,对任一正整数n(n<20),输出所有不超过2n−1的梅森数。
输入格式:
输入在一行中给出正整数n(n<20)。
输出格式:
按从小到大的顺序输出所有不超过2n−1的梅森数,每行一个。如果完全没有,则输出“None”。
输入样例:
6
输出样例:
3
7
31
解题思路:
先满足2^n-1的形式,再计算是否为素数
代码如下:
#include <stdio.h>
#include <math.h>
int main()
{int n,i,c,j,ge=0;scanf("%d",&n);for(i=2;i<=n;i++) //满足梅森数的形式{c=pow(2,i)-1;for(j=2;j<=c-1;j++){if(c%j==0){break; //不是素数}}if(j>c-1) //是素数的条件{printf("%d\n",c); ge++;}}if(ge==0){printf("None");}
}
7-5 单词长度
你的程序要读入一行文本,其中以空格分隔为若干个单词,以.结束。你要输出每个单词的长度。这里的单词与语言无关,可以包括各种符号,比如it's算一个单词,长度为4。注意,行中可能出现连续的空格;最后的.不计算在内。
输入格式:
输入在一行中给出一行文本,以.结束
提示: 用scanf("%c",...);来读入一个字符,直到读到.为止。
输出格式:
在一行中输出这行文本对应的单词的长度,每个长度之间以空格隔开,行末没有最后的空格。
输入样例:
It's great to see you here.
输出样例:
4 5 2 3 3 4
解题思路:
使用循环读取字符,直到读取到 . 字符或者无法继续读取为止。
在循环中,判断当前读取的字符是否为空格。如果是空格,则说明一个单词的长度统计完成,需要输出该单词的长度,并将 wordCount 加一,wordLength 归零。
如果当前字符不是空格,则说明当前字符属于一个单词内部,将 wordLength 加一以统计单词的长度。
循环结束后,需要处理最后一个单词。如果 wordLength 大于0,说明最后一个单词的长度统计完成,需要输出该单词的长度,并将 wordCount 加一。
代码如下:
#include <stdio.h>int main() {char ch;int wordCount = 0; // 单词计数器int wordLength = 0; // 当前单词长度while (scanf("%c", &ch) == 1 && ch != '.') {if (ch == ' ') {if (wordLength > 0) {printf("%d ", wordLength);wordCount++;wordLength = 0;}} else {wordLength++;}}// 输出最后一个单词的长度if (wordLength > 0) {printf("%d", wordLength);wordCount++;}printf("\n");return 0;
}7-6 21循环-求和3
sxtc爱做数学题,今天他又拿到一道数学题:

注意答案有可能很大,请对114514取模。
他希望擅长求和的你帮他解出这个求和问题。
输入格式:
读入两个数n,k。
输出格式:
输出求和结果,请对答案取模114514。
输入样例:
在这里给出一组输入。例如:
11451 4
输出样例:
在这里给出相应的输出。例如:
113968
解题思路:
使用两个嵌套的 for 循环来计算积和求和。外层循环控制变量 i 从1到 n,内层循环控制变量 e 从1到 k。在每次内层循环中,通过 d = (d * c) % 114514 实现了累乘的操作,并将结果存储在变量 d 中。
在外层循环的每次迭代结束后,将 d 累加到变量 f 中,并在累加之前通过 % 114514 运算符对 d 进行取模操作。最后,通过 % 114514 运算符对 f 进行取模操作,并输出结果。
代码如下:
#include <stdio.h>int main() {int n, k;scanf("%d%d", &n, &k);int d = 1;int f = 0;for (int i = 1; i <= n; i++) {for (int e = 1; e <= k; e++) {d = (d * i) % 114514;}f = (f + d) % 114514;d = 1;}printf("%d", f);return 0;
}
7-7 21循环-金字塔
SeraphJACK正在摆积木。他想用这些积木垒成一座金字塔。同时摆好金字塔之后,他为每层积木涂上不同的颜色,这些颜色用从1开始的正整数表示,从最底层开始涂色。现在告诉你SeraphJACK有n块积木,请输出他用这些积木能摆出并涂色的最大金字塔。(金字塔形状详见样例,0表示这个位置没有积木)
输入格式:
一个整数n,1<=n<=1000
输出格式:
涂色后的金字塔
输入样例1:
在这里给出一组输入。例如:
11
输出样例1:
在这里给出相应的输出。例如:
0004000
0030300
0202020
1010101
输入样例2:
在这里给出一组输入。例如:
1
输出样例2:
在这里给出相应的输出。例如:
1
解题思路:
外层使用 for 循环,用于确定金字塔的层数。通过不断增加 b(层数) 的值,直到满足积木数量 b * (b + 1) / 2 大于或等于输入的积木数量 a。
内层嵌套使用两个 while 循环,用于打印每一层的积木。其中,第一个 while 循环控制层数,从第一层开始到倒数第二层。第二个 while 循环控制打印每一层的积木个数和颜色。
在第二个 while 循环中,根据打印位置的关系来判断是否打印积木和积木的颜色。若当前位置在金字塔的边缘或超出边缘范围,则打印0;否则,根据 (d-b+1+c)%2==1 的条件判断来决定打印的颜色。
代码如下:
#include<stdio.h>
int main()
{int a,b,c=1,d;scanf("%d",&a);for(b=1;b*(b+1)/2<=a;b++);while(c<=(b-1)){d=1;while(d<=2*b-3){if(d<=(b-1-c)||d>b-2+c)printf("0");else if((d-b+1+c)%2==1)printf("%d",b-c);else printf("0");d++;}printf("\n");c++;}return 0;
}
3️⃣ 总结
此文为 【C语言必知必会】子系列第六篇 ,通过以题代练的形式带领读者掌握C语言的循环结构,带领读者从0开始,深度掌握知识点。
以题代练对于C语言的学习是十分重要的,专栏将持续提供优质C语言编程题与理论课的学习,带领读者全方位掌握C语言。读者可订阅专栏持续跟进。
相关文章:

【C语言必知必会 | 子系列第六篇】深入剖析循环结构(2)
引言 C语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发。它在编程语言中具有举足轻重的地位。 此文为【C语言必知必会】第六篇,基于进行C语言循环结构的编程题专项练习,结合专题优质题目,带领读者从0开始&…...
华为ICT——云计算基础知识、计算类技术听课笔记
ICT(information and communications technology):信息与通信技术 传统IT架构缺点 TCO:总体拥有成本 云计算模式 云计算价值 云计算通用点 虚拟化技术:将单台物理服务器虚拟为多台虚拟机使用,多台虚拟机共享物理服务器硬件资源。 虚拟化本质…...

PyTorch入门教学——TensorBoard使用
1、TensorBoard简介 TensorBoard是Google开发的一个机器学习可视化工具。其主要用于记录机器学习过程,例如: 记录损失变化、准确率变化等记录图片变化、语音变化、文本变化等。例如在做GAN时,可以过一段时间记录一张生成的图片绘制模型 2、…...

03 里氏替换原则
官方定义: 里氏替换原则(Liskov Substitution Principle,LSP)是由麻省理工学院计算机科学系教授芭芭拉利斯科夫于 1987 年在“面向对象技术的高峰会议”(OOPSLA)上发表的一篇论文《数据抽象和层次》&#…...
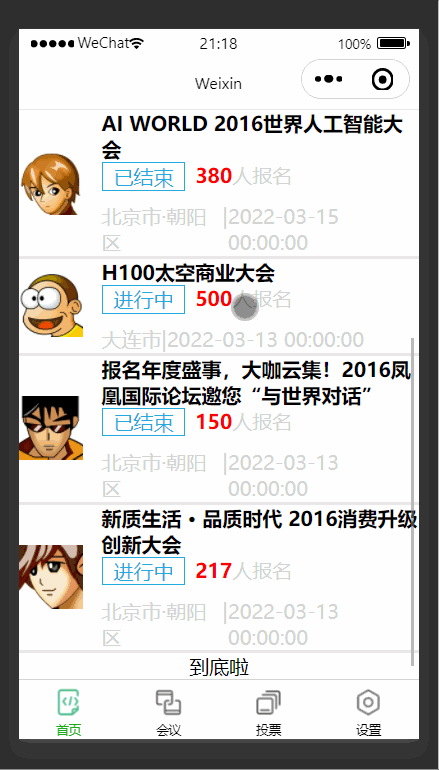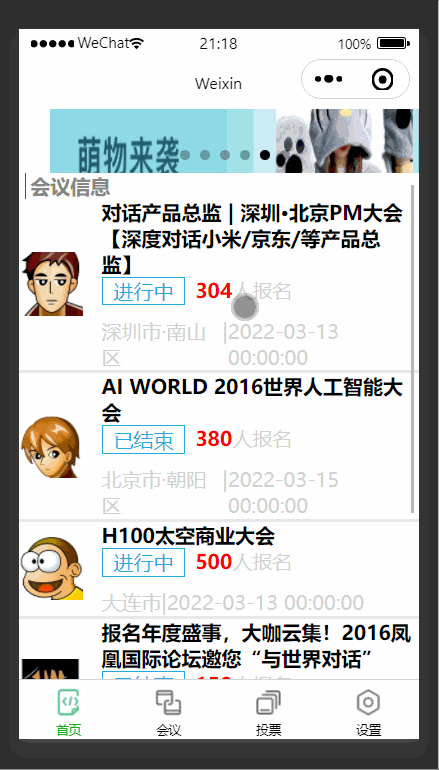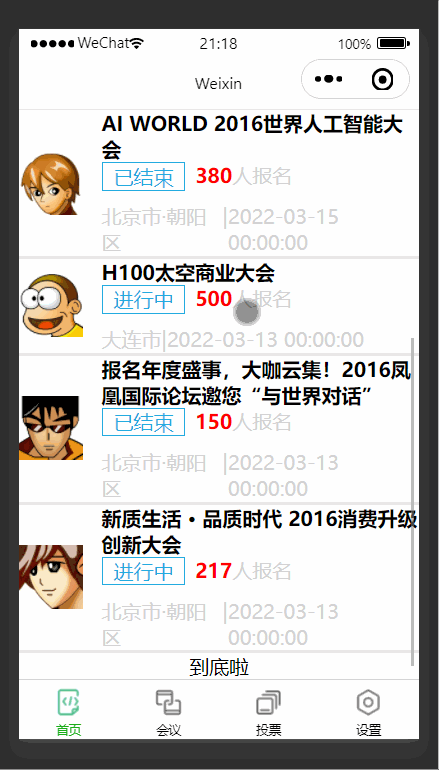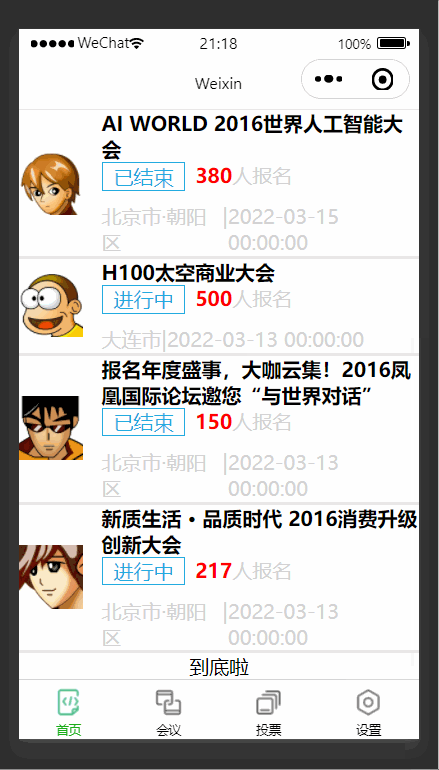
【微信小程序】无纸化会议OA系统之首页搭建
前言 中国政府意识到信息技术的重要性,并开始积极推动信息产业的发展。一系列政策和措施被制定和执行,以促进信息技术的采用和普及,从而推动数字化时代的到来。为了响应国家推行的数字化时代,本篇文章以会议OA系统为背景进行编写…...
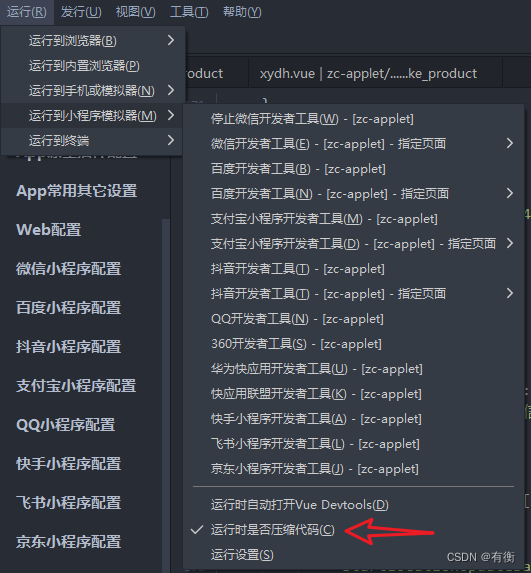
小程序:uniapp解决主包体积过大的问题
已经分包但还是体积过大 运行时勾选“运行时是否压缩代码”进行压缩 在manifest.json配置(开启分包优化) "mp-weixin" : {"optimization" : {"subPackages" : true}//.... },在app.json配置(设置组件按需注入…...
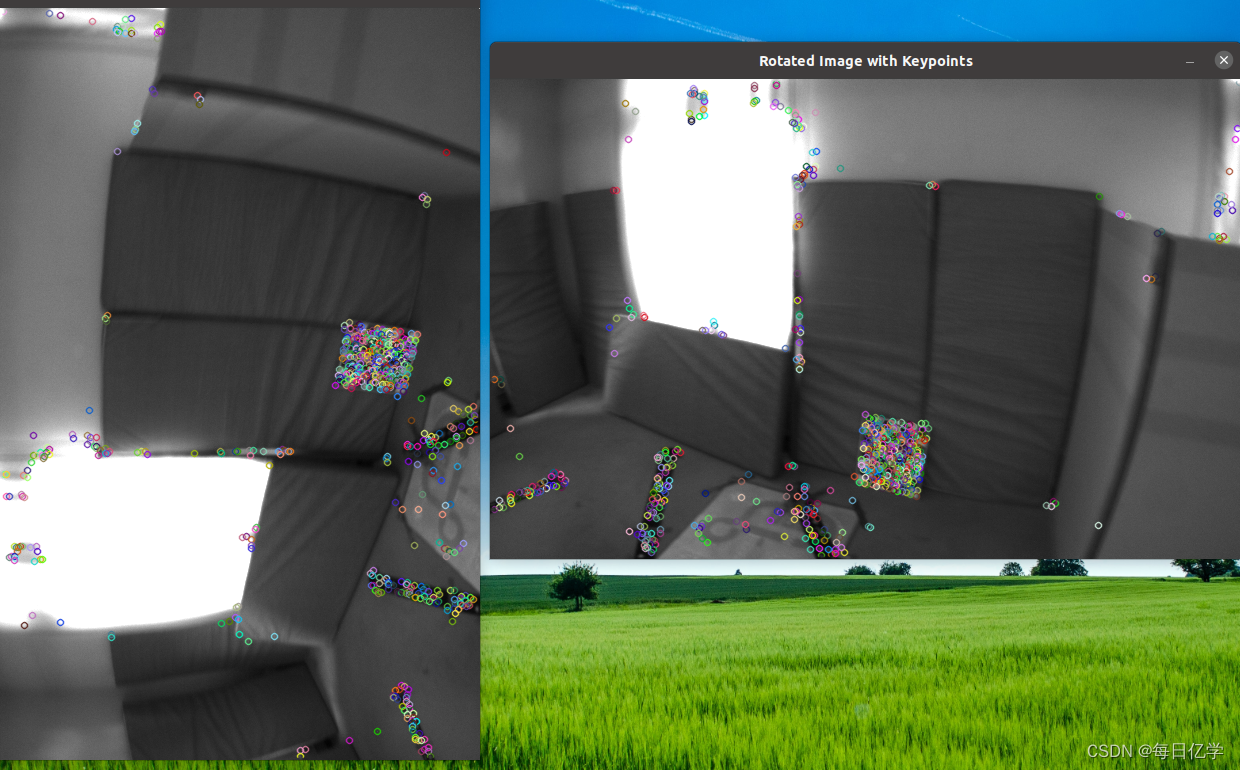
[opencv]图像和特征点旋转
本来说这是很简单的一个内容,图像旋转只需要使用opencv中自带的旋转函数即可完成,但是最近在做特征点旋转的时候发现使用内置rotate函数给图像旋转90度,再用getRotationMatrix2D得出的旋转矩阵对特征点旋转,画出来的特征点位置全部…...

世界粮食日:宏工科技有对策,赋能食品生产高效可持续发展
10月16日是世界粮食日。随着全球人口的增长,人们对高品质食品的需求也越来越大,如何实现“更好生产、更好营养”成为了食品生产与供应的重要话题。15年来,宏工科技专注物料处理自动化领域,提供食品物料处理一站式解决方案以提高生…...

FutureTask配合Thread实现处理有返回结果的源码、逻辑与架构分析
文章目录 1.介绍2.使用示例3.执行过程描述4.整体的关系5.涉及到的核心源码(只提取了关键代码)5.1 Callable5.2 RunnableFuture5.3 FutureTask5.4 Thread 1.介绍 FutureTask 能够接收 Callable 类型的参数,用来处理有返回结果的情况。 2.使用…...

Queue Deque 介绍
目录 一. 前言 二. Queue 接口 三. Deque 接口 一. 前言 Java里有一个叫做Stack的类,却没有叫做Queue的类(它是个接口名字)。当需要使用栈时,Java已不推荐使用Stack,而是推荐使用更高效的ArrayDeque;既然…...

机器学习(23)---Boosting tree(课堂笔记)
文章目录 一、知识记录二、题目2.1 题目12.2 题目22.3 答案书写 一、知识记录 二、题目 2.1 题目1 2.2 题目2 2.3 答案书写...

Excel 导出打不开
$filename iconv("UTF-8", "GB2312//IGNORE", 志愿者列表) . - . date(YmdHis) . .xlsx; header(Content-Type: application/vnd.ms-excel); header(Content-Disposition: attachment;filename".$filename."); header(Cache-Control: max-age0)…...

css钟表数字样式
如图: 代码 font-size: 28px;font-family: Yourname;font-weight: 500;color: #00e8ff;...

一步一步分析ChatGPT,1 粘性,2 传染性, 3 双边网络效应
请按照以下三个维度一步一步分析ChatGPT,1 粘性,2 传染性, 3 双边网络效应,比如亚马逊的买家和商家的关系 ChatGPT的分析 1.1. 粘性 (Stickiness) 定义: 粘性是指产品或服务对用户的吸引力,即用户在使用…...
:阿里巴巴开源的线上问题诊断工具)
Arthas(阿尔萨斯):阿里巴巴开源的线上问题诊断工具
背景 通常,本地开发环境无法访问生产环境。如果在生产环境中遇到问题,则无法使用 IDE 远程调试。更糟糕的是,在生产环境中调试是不可接受的,因为它会暂停所有线程,导致服务暂停。 开发人员可以尝试在测试环境或者预发环境中复现生产环境中的问题。但是,某些问题无法在不同…...

由Django-Session配置引发的反序列化安全问题
漏洞成因 漏洞成因位于目标配置文件settings.py下 关于这两个配置项 SESSION_ENGINE: 在Django中,SESSION_ENGINE 是一个设置项,用于指定用于存储和处理会话(session)数据的引擎。 SESSION_ENGINE 设置项允许您选择不…...

16-spring AOP核心对象的创建
文章目录 1. aop的几个重要概念2. aop bean definition3. AspectJPointcutAdvisor4.AopConfigUtils5.AnnotationAwareAspectJAutoProxyCreator6. 循环依赖1. aop的几个重要概念 参考官方解释:https://docs.spring.io/spring-framework/docs/5.2.9.RELEASE/spring-framework-r…...

Golang 泛型的介绍
引言 Golang是一种现代的编程语言,以其简洁的语法和高效的性能而闻名。然而,与其他一些编程语言相比,Golang在语言层面上缺乏泛型的支持,这使得在处理不同类型的数据时变得有些困难。在本文中,我们将介绍Golang泛型的…...
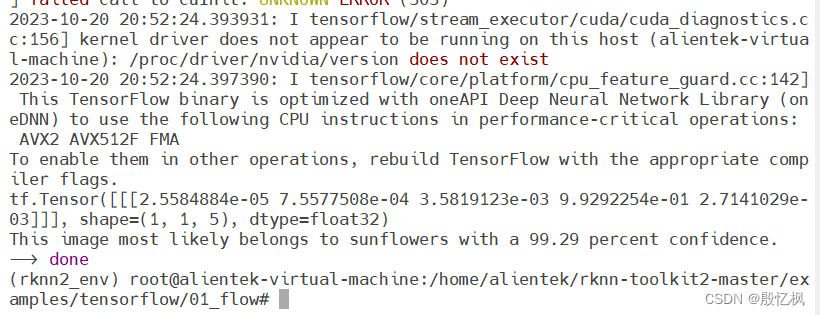
RK3568笔记四:基于TensorFlow花卉图像分类部署
若该文为原创文章,转载请注明原文出处。 基于正点原子的ATK-DLRK3568部署测试。 花卉图像分类任务,使用使用 tf.keras.Sequential 模型,简单构建模型,然后转换成 RKNN 模型部署到ATK-DLRK3568板子上。 在 PC 使用 Windows 系统…...

甄知科技张礼军:数智化转型助企业破茧成蝶!
数智化浪潮滚滚向前,正席卷各行各业,带领企业从数字化时代跨入数智化时代。可什么是数智化?如何实现数智化转型?已经成为横亘在无数企业面前的大难题! 事实上,数智化是数字化、AI和业务三个要素的交集&…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
