22-数据结构-内部排序-选择排序
简介:每一趟选择最小或最大的一个,排在前面或后面。主要右简单选择排序和堆排序
一、简单选择排序
1.1简介:
每趟选择最小的,放在前面,一次类推,代码思想:两个循环,外循环是趟数,内循环是选择最小下标,最后进行交换值,达到排序的目的。
时间复杂度:O()
空间复杂度:O(1)
稳定性:不稳定,交换时,可能与另一个关键字相同的位置发生改变,
适用性:顺序表,链表都可以
比较次数与初始序列无关:基数排序、简单选择排序,折半插入排序
1.2代码:
#include <stdio.h>
void swap(int *a,int *b)
{int temp=(*a);(*a)=(*b);(*b)=temp;
}
void SelectSort(int *a,int n)
{int i,j;for(i=0;i<n-1;i++)//趟数 {int min=i;for(j=i+1;j<n;j++)//查找本趟中最小的一个位置,更新min {if(a[j]<a[min])min=j;}//如果min跟开始不同,则交换位置 if(min!=i) swap(&a[min],&a[i]);}
}
int main()
{int a[6]={5,6,8,9,1,2};SelectSort(a,6);PrintSort(a,6);return 0;} 二、堆排序
1.1简介:
堆分为大根堆和小根堆。大根堆为:逻辑上,是个二叉树,给一维数组按层次遍历,弄成二叉树,然后大根堆是每个子树的根都比左右孩子大。同理小根堆每个子树的根都比左右孩子小。
1.1.1.大小根堆堆排序
- 堆调整,即从最后一个非叶子结点开始,自下而上,自右而左,以非叶子结点为根,在其树中找最大的,作为根,然后调整,最后调整到整个树的根后,再整体看是否需要再调整,最后所有的根都是其所在树的最大结点为止。
- 给最大值沉底。初始化调整完,就给第一个元素和最后一个元素互换,此时给最大值换到了最后面,下次再大根堆调整就不带上这个最大值了,每次调整完,互换后,长度减1个。

1.1.2.根堆的插入和删除
插入的新元素要放在表尾,然后再根据大根堆或小根堆原则,进行堆调整即可。
在堆中删除元素,直接删除,然后用堆尾的元素补到删除位置处,随后再根据大根堆或小根堆原则,进行堆调整即可。
1.1.3.性能
时间复杂度:O()
空间复杂度:O(1)
稳定性:不稳定,可能给后面相同关键字调整到前面,相对位置发生改变
选择性:遇到选出前多少个元素的,算法选择堆排序最优。
1.2代码:
1.2.1.初始化大根堆代码
//整体大根堆初始化
void BulidMaxHeap(int *a,int len)
{int i;for(i=len/2;i>0;--i)//从最后一个非叶子结点开始,依次往前遍历,每次遍历的时候进行堆调整 {HeadAdjust(a,i,len); }
}
//大根堆调整
void HeadAdjust(int *a,int k,int len)
{a[0]=a[k];//a[0]存储原来k的值 int i;for(i=2*k;i<=len;i=i*2)//判断以k为根的两个孩子谁打 {if(i<len && a[i]<a[i+1])i++;//为了防止原a[k]乱跑,拿a[0]进行比较if(a[0]>=a[i]) break; //让根与孩子比较,如果根大于孩子,则符合大根堆 else//不符合的话 {a[k]=a[i];//让大的孩子,赋值给根,覆盖掉 k=i; //然后给原根的坐标挪到孩子处, } } a[k]=a[0];//原根的坐标挪到孩子处,进入第二轮循环,i=i*2,新的堆看是否符合大根堆
} 1.2.2.大根堆排序
void HeadSort(int *a,int len)
{BulidMaxHeap(a,len);//初始化大根堆//排序int i;for(i=len;i>0;--i){swap(&a[1],&a[i]);HeadAdjust(a,1,i-1);//交换后最大值沉底,再进行大根堆调整时,不需要计算最后一个了所以长度为i-1;
} 1.3.总代码:
#include <stdio.h>
//打印大根堆,从下标1打印,0处为哨兵,存储原二叉树,根的值
void PrintSort(int *a,int n)
{int i;for(i=1;i<n;i++){printf("%d ",a[i]);}printf("\n");
}
//交换
void swap(int *a,int *b)
{int temp=(*a);(*a)=(*b);(*b)=temp;
}
//堆排序
//整体大根堆初始化
void BulidMaxHeap(int *a,int len)
{int i;for(i=len/2;i>0;--i)//从最后一个非叶子结点开始,依次往前遍历,每次遍历的时候进行堆调整 {HeadAdjust(a,i,len); }
}
//大根堆调整
void HeadAdjust(int *a,int k,int len)
{a[0]=a[k];//a[0]存储原来k的值 int i;for(i=2*k;i<=len;i=i*2)//判断以k为根的两个孩子谁打 {if(i<len && a[i]<a[i+1])i++;//为了防止原a[k]乱跑,拿a[0]进行比较if(a[0]>=a[i]) break; //让根与孩子比较,如果根大于孩子,则符合大根堆 else//不符合的话 {a[k]=a[i];//让大的孩子,赋值给根,覆盖掉 k=i; //然后给原根的坐标挪到孩子处, } } a[k]=a[0];//原根的坐标挪到孩子处,进入第二轮循环,i=i*2,新的堆看是否符合大根堆
} void HeadSort(int *a,int len)
{BulidMaxHeap(a,len);//初始化大根堆//排序int i;for(i=len;i>0;--i){swap(&a[1],&a[i]);HeadAdjust(a,1,i-1);//每次排序排一个,随后以1为根的二叉树,进行堆调整 }
}
int main()
{int a[9]={0,53,45,87,32,17,65,78,9};HeadSort(a,8);//数组和有效数据PrintSort(a,9);//数组和数组长度return 0;} 相关文章:
22-数据结构-内部排序-选择排序
简介:每一趟选择最小或最大的一个,排在前面或后面。主要右简单选择排序和堆排序 一、简单选择排序 1.1简介: 每趟选择最小的,放在前面,一次类推,代码思想:两个循环,外循环是趟数&a…...

utf8和utf8mb4字符集
柠檬(图片)派 有个玩家取了个名字,名字里带柠檬的图片。在发邮件的时候,要把玩家名字拼装成json格式,存储在mysql表中。 C代码和python代码处理都是正常的,但是调用pymysql的接口,执行sql写入到mysql时。 pymysql会报错…...

前端学成在线项目详细解析一
学成在线项目 01-项目目录 网站根目录是指存放网站的第一层文件夹,内部包含当前网站的所有素材,包含 HTML、CSS、图片、JavaScript等等。 首页引入CSS文件 <!-- 顺序要求:先清除再设置 --> <link rel"stylesheet" hre…...
Redis之UV统计
HyperLogLog 首先我们搞懂两个概念: UV:全称Unique Visitor,也叫独立访客量,是指通过互联网访问、浏览这个网页的自然人。1天内同一个用户多次访问该网站,只记录1次。PV:全称Page View,也叫页…...

sqlserver数据库,创建作业,定时执行sql
1 在业务中涉及到定时操作数据表时,可以设置定时作业。先创建一个存储过程,实现要定时执行的业务。 USE [MyDB] go create procedure [PROC_MYPROCEDURE] name varchar(50), score int, remark varchar(50) AS BEGIN insert into [mytable] values (n…...

计算机缺失d3dcompiler_47.dll解决方案,如何修复电脑缺失d3d文件
在计算机系统中,DLL文件(动态链接库)是一种重要的共享库,它包含了可被多个程序使用的代码和数据。然而,当某些DLL文件丢失或损坏时,可能会导致程序无法正常运行。本文将介绍四种解决D3DCompiler_47.dll缺失…...
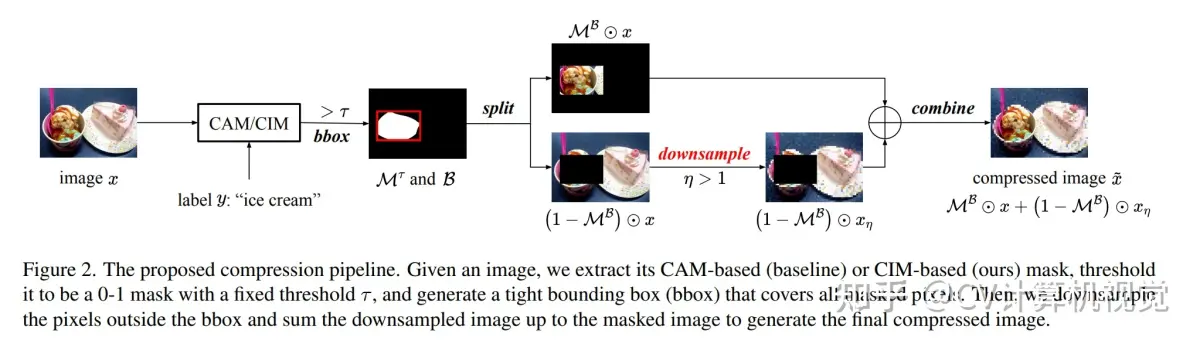
计算机视觉开源代码汇总
1.【基础网络架构】Regularization of polynomial networks for image recognition 论文地址:https://arxiv.org/pdf/2303.13896.pdf 开源代码:https://github.com/grigorisg9gr/regularized_polynomials 2.【目标检测:域自适应】2PCNet: Two-Phase Cons…...

【C语言必知必会 | 子系列第六篇】深入剖析循环结构(2)
引言 C语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发。它在编程语言中具有举足轻重的地位。 此文为【C语言必知必会】第六篇,基于进行C语言循环结构的编程题专项练习,结合专题优质题目,带领读者从0开始&…...
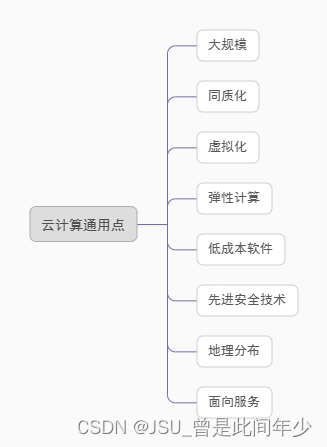
华为ICT——云计算基础知识、计算类技术听课笔记
ICT(information and communications technology):信息与通信技术 传统IT架构缺点 TCO:总体拥有成本 云计算模式 云计算价值 云计算通用点 虚拟化技术:将单台物理服务器虚拟为多台虚拟机使用,多台虚拟机共享物理服务器硬件资源。 虚拟化本质…...

PyTorch入门教学——TensorBoard使用
1、TensorBoard简介 TensorBoard是Google开发的一个机器学习可视化工具。其主要用于记录机器学习过程,例如: 记录损失变化、准确率变化等记录图片变化、语音变化、文本变化等。例如在做GAN时,可以过一段时间记录一张生成的图片绘制模型 2、…...

03 里氏替换原则
官方定义: 里氏替换原则(Liskov Substitution Principle,LSP)是由麻省理工学院计算机科学系教授芭芭拉利斯科夫于 1987 年在“面向对象技术的高峰会议”(OOPSLA)上发表的一篇论文《数据抽象和层次》&#…...
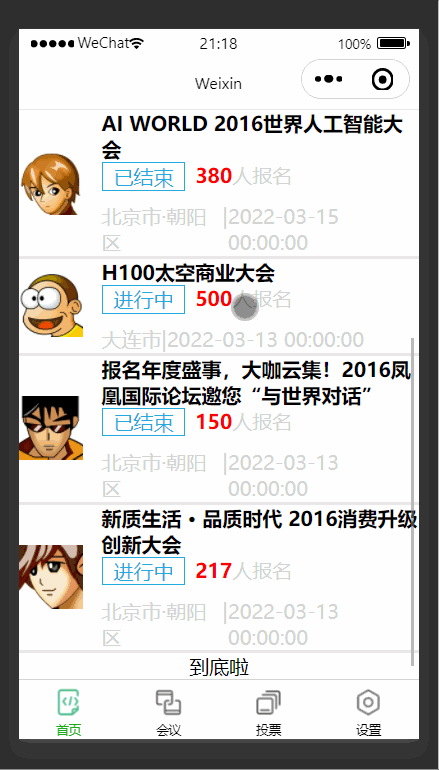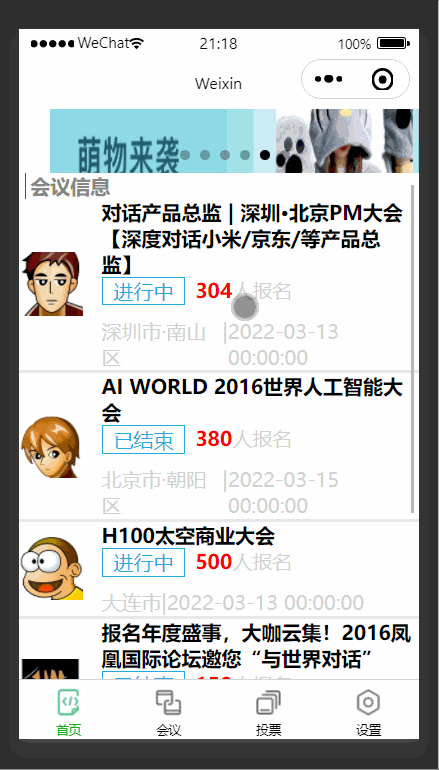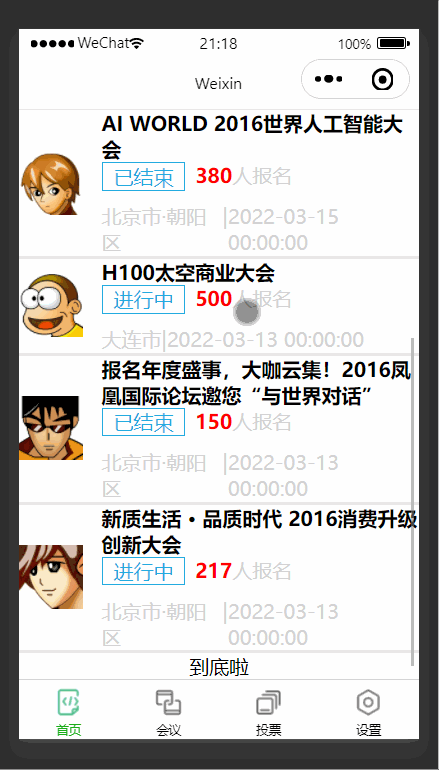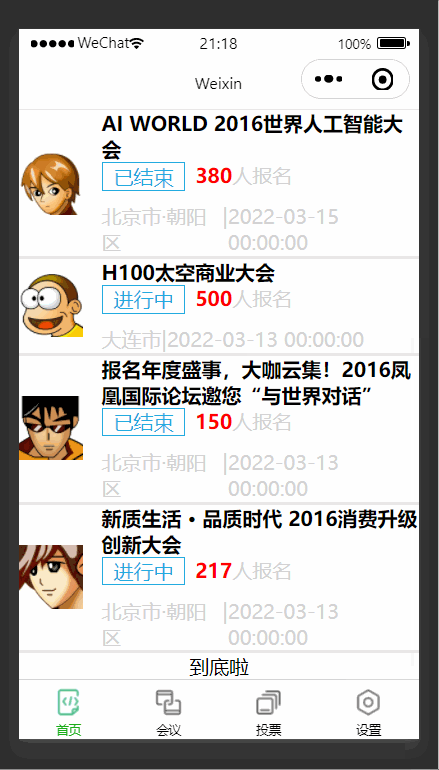
【微信小程序】无纸化会议OA系统之首页搭建
前言 中国政府意识到信息技术的重要性,并开始积极推动信息产业的发展。一系列政策和措施被制定和执行,以促进信息技术的采用和普及,从而推动数字化时代的到来。为了响应国家推行的数字化时代,本篇文章以会议OA系统为背景进行编写…...
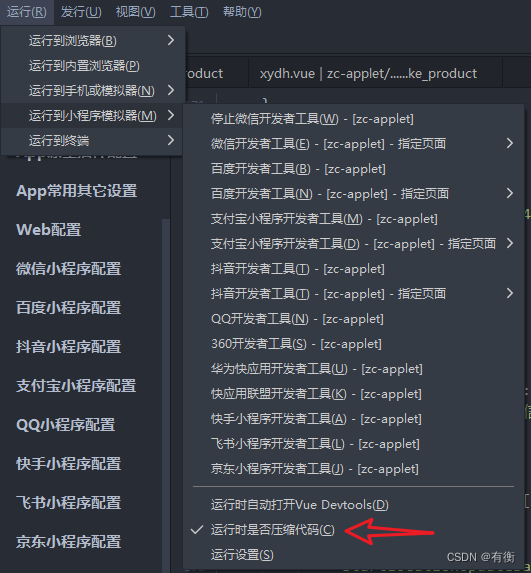
小程序:uniapp解决主包体积过大的问题
已经分包但还是体积过大 运行时勾选“运行时是否压缩代码”进行压缩 在manifest.json配置(开启分包优化) "mp-weixin" : {"optimization" : {"subPackages" : true}//.... },在app.json配置(设置组件按需注入…...
[opencv]图像和特征点旋转
本来说这是很简单的一个内容,图像旋转只需要使用opencv中自带的旋转函数即可完成,但是最近在做特征点旋转的时候发现使用内置rotate函数给图像旋转90度,再用getRotationMatrix2D得出的旋转矩阵对特征点旋转,画出来的特征点位置全部…...

世界粮食日:宏工科技有对策,赋能食品生产高效可持续发展
10月16日是世界粮食日。随着全球人口的增长,人们对高品质食品的需求也越来越大,如何实现“更好生产、更好营养”成为了食品生产与供应的重要话题。15年来,宏工科技专注物料处理自动化领域,提供食品物料处理一站式解决方案以提高生…...

FutureTask配合Thread实现处理有返回结果的源码、逻辑与架构分析
文章目录 1.介绍2.使用示例3.执行过程描述4.整体的关系5.涉及到的核心源码(只提取了关键代码)5.1 Callable5.2 RunnableFuture5.3 FutureTask5.4 Thread 1.介绍 FutureTask 能够接收 Callable 类型的参数,用来处理有返回结果的情况。 2.使用…...

Queue Deque 介绍
目录 一. 前言 二. Queue 接口 三. Deque 接口 一. 前言 Java里有一个叫做Stack的类,却没有叫做Queue的类(它是个接口名字)。当需要使用栈时,Java已不推荐使用Stack,而是推荐使用更高效的ArrayDeque;既然…...

机器学习(23)---Boosting tree(课堂笔记)
文章目录 一、知识记录二、题目2.1 题目12.2 题目22.3 答案书写 一、知识记录 二、题目 2.1 题目1 2.2 题目2 2.3 答案书写...

Excel 导出打不开
$filename iconv("UTF-8", "GB2312//IGNORE", 志愿者列表) . - . date(YmdHis) . .xlsx; header(Content-Type: application/vnd.ms-excel); header(Content-Disposition: attachment;filename".$filename."); header(Cache-Control: max-age0)…...

css钟表数字样式
如图: 代码 font-size: 28px;font-family: Yourname;font-weight: 500;color: #00e8ff;...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
