用c++写一个高精度计算的减法运算
这段代码是一个用C++编写的程序,它实现了两个大整数的减法运算。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;int main(){int a[256],b[256],c[256],lena,lenb,lenc,i;char n[256],n1[256]="1001",n2[256]="2001";//n1被减数,n2减数memset(a,0,sizeof(a));//memset用于初始化数组或一块内存区域,将其中的每个字节都设置为指定的值。将数组a的值全部初始化为0memset(b,0,sizeof(b));memset(c,0,sizeof(c));//如果被减数小于减数,则交换它们的值,并输出负号表示结果将为负数。if(strlen(n1)<strlen(n2)||(strlen(n1)==strlen(n2)&&strcmp(n1,n2)<0)){strcpy(n,n1);strcpy(n1,n2);strcpy(n2,n);cout<<"-";}lena=strlen(n1);lenb=strlen(n2);for(i=0;i<=lena-1;i++){a[lena-i]=int(n1[i]-'0');}for(i=0;i<=lenb-1;i++){a[lenb-i]=int(n2[i]-'0');}i=1;while(i<=lena||i<=lenb){if(a[i]<b[i]){a[i]+=10;//不够减,那么想高位借1当10a[i+1]--;}c[i]=a[i]-b[i];//对应位相减i++;}lenc=i;while((c[lenc]==0)&&(lenc>1)) {lenc--;//最高位的0不输出}for(i=lenc;i>=1;i--) {cout<<c[i];}cout<<endl;return 0;
}代码解析
-
字符数组的使用:这段代码使用字符数组来存储大整数。大整数通常无法用标准整数类型来表示,因此需要将其分解为字符数组,然后进行逐位操作。
-
memset函数:memset用于初始化数组或内存区域,将每个字节都设置为指定的值。在这里,它用来初始化a、b和c数组的所有元素为0。 -
字符转整数的转换:代码中使用
int(n1[i]-'0')将字符数字转换为整数。这是因为字符 ‘0’ 到 ‘9’ 在 ASCII 编码中是连续的,所以可以通过减去 ‘0’ 来获得对应的整数值。 -
大整数运算的思想:最重要的理解点是大整数运算的思想。由于大整数超出了标准整数范围,因此需要将它们分解为字符数组,并模拟手工计算的过程。这包括逐位减法和借位的概念。
逐位减法:
- 在大整数运算中,当我们需要计算两个大整数的差值时,通常需要从最低位(个位)开始逐位相减。
- 例如,如果我们要计算 7654321 减去 1234567,我们从右向左逐位相减,从个位开始。首先是 1 减去 7,由于 1 小于 7,需要借位。这产生了一个新的问题,即借位的概念。
- 逐位减法的关键是要确保每一位的减法操作都得到正确的结果,同时考虑到借位。
借位:
- 借位是指在执行逐位减法时,如果被减数小于减数,就必须向高位借位来执行减法。这类似于在十进制数学中,当你从某一位借位时,需要在高位的数字中减去一个。
- 例如,在上面的示例中,1 减去 7 时,因为 1 小于 7,所以需要向高位借位。这导致 6(10 减去 7),并且高位的 6 会减去 1,以确保减法操作是正确的。
- 借位可以一直传递到更高位,直到没有借位为止。
相关文章:

用c++写一个高精度计算的减法运算
这段代码是一个用C编写的程序,它实现了两个大整数的减法运算。 #include<iostream> #include<cstdio> #include<cstring> using namespace std;int main(){int a[256],b[256],c[256],lena,lenb,lenc,i;char n[256],n1[256]"1001",n2[2…...

基于白鲸优化的BP神经网络(分类应用) - 附代码
基于白鲸优化的BP神经网络(分类应用) - 附代码 文章目录 基于白鲸优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.白鲸优化BP神经网络3.1 BP神经网络参数设置3.2 白鲸算法应用 4.测试结果:5.M…...
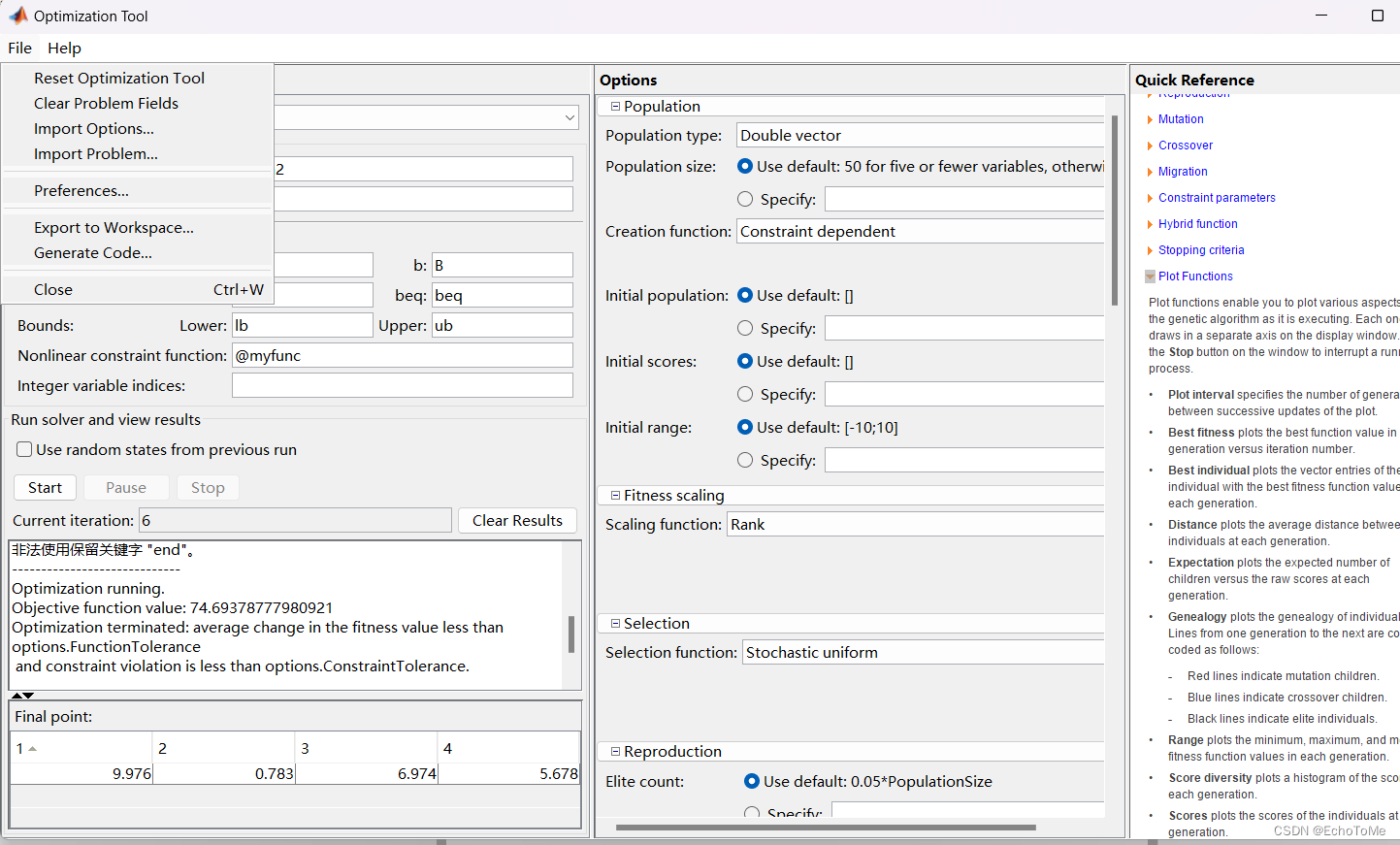
Matlab遗传算法工具箱——一个例子搞懂遗传算法
解决问题 我们一般使用遗传算法是用来处理最优解问题的,下面是一个最优解问题的例子 打开遗传算法工具箱 ①在Matlab界面找到应用程序选项,点击应用程序(英文版的Matlab可以点击App选项) ②找到Optimization工具箱,点击打开 创建所需要…...
Coreldraw2020最新64位电脑完整版本下载教程
安装之前所有的杀毒软件都要退出。无论是360,腾讯管家,或者电脑自带的安全中心,要不然会阻止安装。 CorelDRAW2020版win下载如下:https://wm.makeding.com/iclk/?zoneid55678 CorelDRAW2020版mac下载如下:https://wm.makeding.com/iclk/?…...
第一节——vue安装+前端工程化
作者:尤雨溪 官网:简介 | Vue.js 脚手架文档 创建一个项目 | Vue CLI 一、概念(了解) 是一套用于构建用户界面的渐进式框架。与其它大型框架不同的是,Vue 被设计为可以自底向上逐层应用。Vue 的核心库只关注视图层&…...
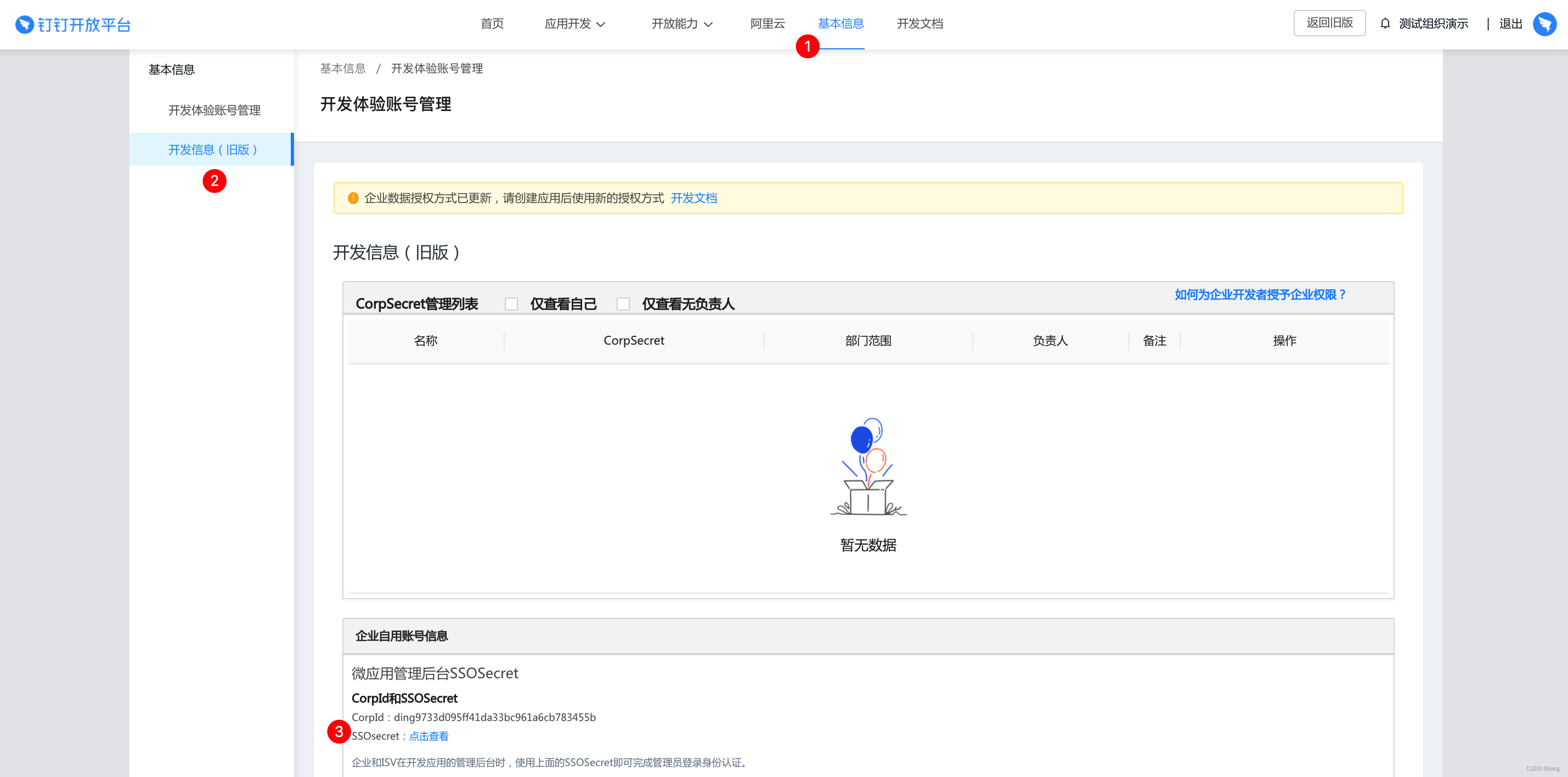
vue集成钉钉单点登录
初始环境判断 判断是否是来自钉钉环境的访问,返回:boolean类型值 window.navigator.userAgent.includes("DingTalk")前端引入vue中钉钉相关的依赖,并获取钉钉的临时授权码 import * as dingtalk from dingtalk-jsapi; let that …...
凉鞋的 Godot 笔记 203. 变量的常用类型
203. 变量的常用类型 在上一篇,我们对变量进行了概述和简介,知识地图如下: 我们已经接触了,变量的字符串类型,以及一些功能。 在这一篇,我们尝试多接触一些变量的类型。 首先是整数类型。 整数类型 整…...

【现场问题】批量新建工作流的问题
批量建工作流的优势和劣势 关于批量建工作流的优势缺点 关于批量建工作流的优势 不需要手动,直接一键建立,同时节点的批量建立也成功了 缺点 1、机器识别,一次性成形,没有办法手动的去干涉这东西 2、大数据量的表需要单独处理的…...
)
动态规划14(Leetcode516最长回文子序列)
代码: class Solution {public int longestPalindromeSubseq(String s) {int n s.length();int[][] dp new int[n][n];for(int in-1;i>0;i--){dp[i][i] 1;char c1 s.charAt(i);for(int ji1;j<n;j){char c2 s.charAt(j);if(c1c2){dp[i][j] dp[i1][j-1]2…...
 简介和目标)
写一个简单的解释器(0) 简介和目标
解释语言和编译语言 编译语言,是指其编译器生成的可执行文件为机器码,可以直接在计算机上运行的语言,比如说 C/C \texttt{C/C} C/C 。 解释语言,是指经由解释器生成的可执行文件为字节码文件,只能运行在特殊的虚拟机…...

通过Chain Prompts方式将LLM的能力引入测试平台:正交实验测试用例生成
通过Chain Prompts方式将LLM的能力引入测试平台:正交实验测试用例生成 Chain Prompts Chain Prompts是指在一个对话或文本生成任务中,将前一个提示的输出作为下一个提示的输入,形成一个连续的链条。这种方法常常用于创建连贯的、有上下文关联的文本。在对话系统中,这种方…...

M-BUS和modbus的区别是什么?
M-BUS与Modbus是两种在工业自动化和楼宇自动化领域广泛应用的通信协议。那么,这两种通信协议有哪些区别呢?下面,就由小编带大家一起来了解下吧! 一、简介 M-BUS(Multi-dropBus,多点通信总线)和Modbus(莫迪波特率)都是用于设备和系统之间通信…...

CSS 滚动驱动动画 timeline-scope
timeline-scope 语法兼容性 timeline-scope 看到 scope 就知道这个属性是和范围有关, 没错, timeline-scope 就是用来修改一个具名时间线(named animation timeline)的范围. 我们介绍过的两种时间线 scroll progress timeline 和 view progress timeline, 使用这两种时间线(通…...

R语言时间序列分析
目录 概述 1、什么是时间序列分析 2、时间序列分析的应用 时间序列的基本操作...

房产中介小程序,二手房小程序带H5公众号,房产门户PC版,房产中介,房产经纪人
套餐一:源码=1500 套餐二:全包服务 包服务器+APP+认证小程序+H5+PC+采集=2000(全包服务三年) 可以封装打包APP 一、付费发布信息 支持付费发布、刷新、置顶房源信息; 二、个人发布信息 支持个人和房产经纪人发布房源信息; 三、新房楼盘模块 支持新房楼盘功能,后台添加…...

Docker 部署
1 完全清除旧版本docker for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; doneImages, containers, volumes, and networks stored in /var/lib/docker/ arent automatically removed when y…...
)
ffmpeg推流+nginx转发+拉流(RTMP拉流)
参考:https://blog.csdn.net/weixin_43796767/article/details/117307845 1.搭建支持rtmp转发的nginx服务 git clone https://github.com/arut/nginx-rtmp-module wget http://nginx.org/download/nginx-1.8.0.tar.gz tar -xvf nginx-1.8.0.tar.gz cd nginx-1.8.0/ ./confi…...
)
【Python第三方包】解析和生成二维码(pyqrcode包)
文章目录 前言一、安装pyqrcode包二、生成二维码2.1 二维码生成基础使用2.2 自定义二维码样式颜色设置错误纠正级别尺寸设置三、解析二维码总结前言 在现代信息时代,二维码(QR码)已经成为了快速传递信息的常见方式。Python提供了多种第三方包,用于生成和解析二维码。其中,…...

自适应键盘高度
自适应系统键盘 背景代码demo 背景 键盘高度无法获取,倒是输入框抖动问题 代码 设置 android:windowSoftInputMode“adjustNothing” public class KeyBoardHelper {private static final String TAG "KeyBoardHeightHelper";private PopupWindow po…...
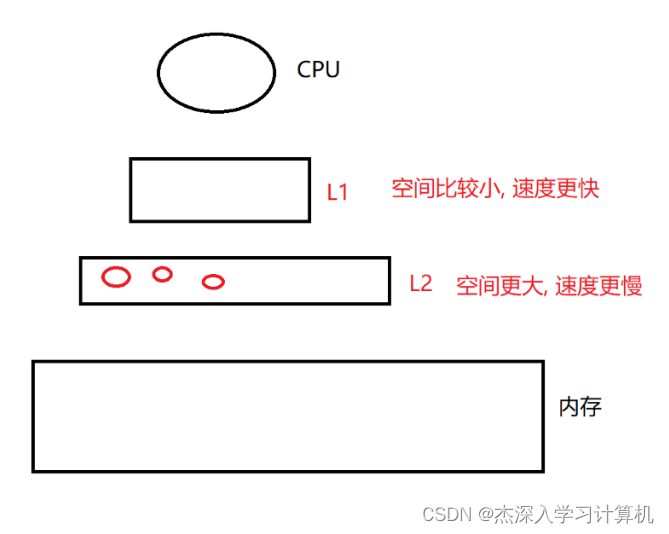
【JavaEE】计算机是如何工作的
计算机是如何工作的 冯诺依曼体系操作系统操作系统的概念与定位进程和任务操作系统对进程的管理PCB 的相关信息 冯诺依曼体系 现代的大多数计算机, 都遵循冯诺依曼体系 CPU 中央处理器: 进行算术运算和逻辑判断存储器: 分为外存和内存, 用于存储数据(使用二进制方式存储)输入…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
