LC-2316. 统计无向图中无法互相到达点对数(DFS、并查集)
2316. 统计无向图中无法互相到达点对数
中等
给你一个整数 n ,表示一张 无向图 中有 n 个节点,编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。
示例 1:

输入:n = 3, edges = [[0,1],[0,2],[1,2]]
输出:0
解释:所有点都能互相到达,意味着没有点对无法互相到达,所以我们返回 0 。
示例 2:
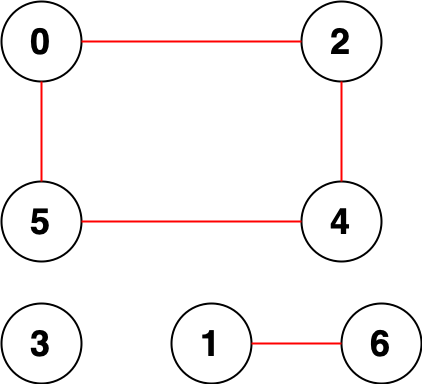
输入:n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出:14
解释:总共有 14 个点对互相无法到达:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。
提示:
1 <= n <= 1050 <= edges.length <= 2 * 105edges[i].length == 20 <= ai, bi < nai != bi- 不会有重复边。
DFS
class Solution {// 统计联通分量 个数 和 大小// 然后递推,求出点对个数// 例如 4 1 2// 4 * 1 + 5 * 2public long countPairs(int n, int[][] edges) {List<Integer>[] g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for(int[] e : edges){int x = e[0], y = e[1];g[x].add(y);g[y].add(x);}boolean[] vis = new boolean[n];List<Integer> list = new ArrayList<>();for(int i = 0; i < n; i++){if(!vis[i]){int cnt = dfs(i, -1, g, vis);list.add(cnt);}}long res = 0l, sum = 0l;for(Integer e : list){res += e * sum;sum += e;}return res;}private int dfs(int x, int fa, List<Integer>[] g, boolean[] vis){int res = 1;vis[x] = true;for(int y : g[x]){if(y != fa && !vis[y])res += dfs(y, x, g, vis);}return res;}
}
并查集
统计连通块大小可以用并查集做
class Solution {// 统计联通分量 个数 和 大小public long countPairs(int n, int[][] edges) {UF uf = new UF(n);for(int[] e : edges){uf.union(Math.max(e[0], e[1]), Math.min(e[0], e[1]));}Map<Integer, Integer> map = new HashMap<>();for(int i = 0; i < n; i++){map.merge(uf.find(i), 1, Integer::sum);}long res = 0l, sum = 0l;for(int x : map.keySet()){res += (long)map.get(x) * sum;sum += map.get(x);}return res;}
}/* ------------ 并查集模版 ------------ */
class UF {int[] parent; // par数组用来存储根节点,par[x]=y表示x的根节点为yint[] size; // size[i]表示以i为根的联通块大小int count; // count表示连通块个数,每次调用union时count-1public UF(int n) {this.count = n;parent = new int[n];size = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;size[i] = 1;}}public void union(int x, int y) {int rootx = find(x);int rooty = find(y);if (rootx == rooty) return;else//不是同一个根,即不在同一个集合,就合并parent[rootx] = rooty;size[rooty] += size[rootx];count--;}public int find(int x) {// 路径压缩if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}
}相关文章:

LC-2316. 统计无向图中无法互相到达点对数(DFS、并查集)
2316. 统计无向图中无法互相到达点对数 中等 给你一个整数 n ,表示一张 无向图 中有 n 个节点,编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。 请你返回 无法互相…...

git笔记 - 常用记录
第1阶段 - Git简介 什么是Git及其重要性?基本的Git概念和术语 仓库(Repository):也称为 repo,是存储代码和版本历史的地方。它可以是本地仓库(在本地计算机上)或远程仓库(在服务器…...
无纸化办公小程序数据交互、wxs的使用
前言 很多同志们再写小程序的过程中,不知道该怎么发起HTTP请求到后端,在Web环境中发起HTTPS请求是很常见的,但是微信小程序是腾讯内部的产品,不能直接打开一个外部的链接。例如,在微信小程序中不能直接打开www.taobao…...
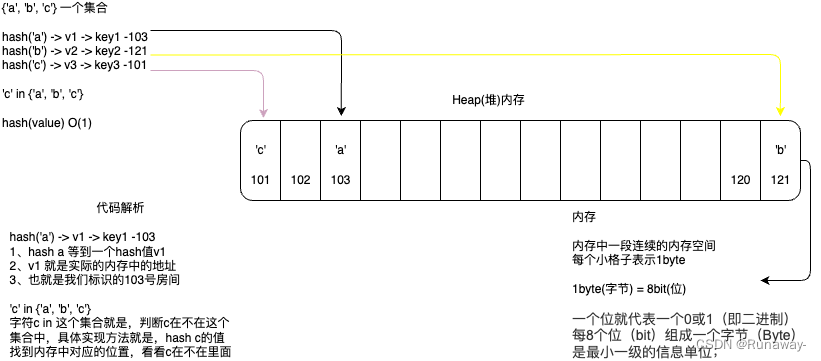
Python之哈希表-哈希表原理
Python之哈希表-哈希表原理 集合Set 集合,简称集。由任意个元素构成的集体。高级语言都实现了这个非常重要的数据结构类型。Python中,它是可变的、无序的、不重复的元素的集合 初始化 set() -> new empty set objectset(iterable) -> new set …...
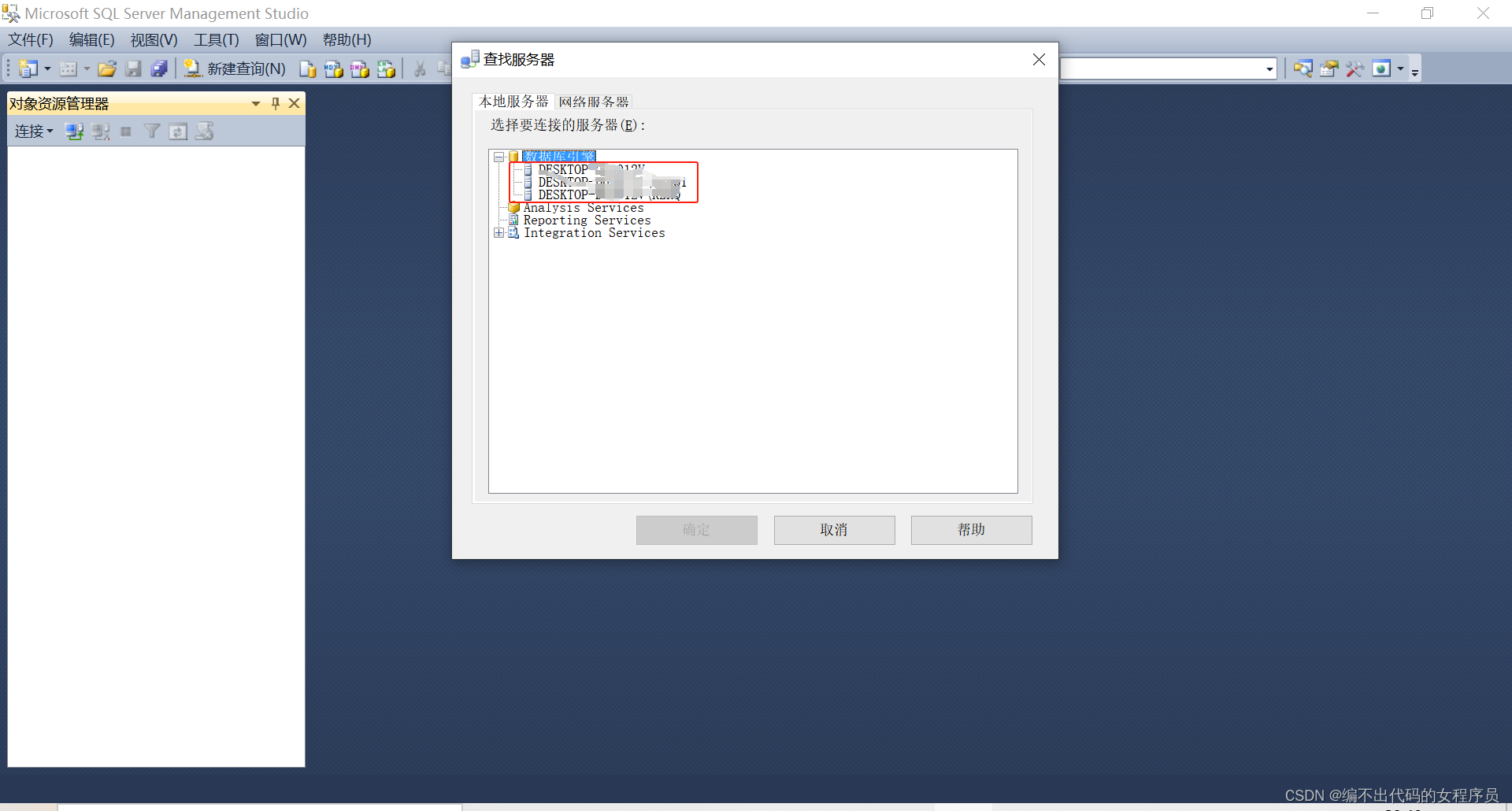
sql server2014如何添加多个实例 | 以及如何删除多个实例中的单个实例
标题sql server2014如何添加多个实例 前提(已安装sql server2014 且已有默认实例MSSQLSERVER) 添加新的实例 其实就是根据安装步骤再安装一次(区别在过程中说明) 双击安装 选择“全新独立安装或添加现有功能” 然后下一步下一…...

C++ 智能指针常用总结
C 智能指针常用总结 文章目录 C 智能指针常用总结1. 写在对前面2. why 智能指针3. what 智能指针3.1 unique_ptr3.2 shared_ptr3.3 weak_ptr 3. how 指针指针3.1 unique_ptr3.1.1 创建3.1.2 成员函数 3.2 shared_ptr3.2.1创建3.2.2 成员对象 3.3 weak_ptr 4. 碎碎念5.参考资料 …...

OracleRAC 安装配置过程中的问题
OS RHAS 3.2 DB 9204 在RAC的安装配置过程中,虽然是严格仔细按照文档来实施,但还是出现不少问题,现整理出来。 现象一 : 在节点一安装数据库的时候出现以下错误 [oraclerac1 dbs]$ sqlplus "/nolog"SQL*Plus: Relea…...

基于战争策略优化的BP神经网络(分类应用) - 附代码
基于战争策略优化的BP神经网络(分类应用) - 附代码 文章目录 基于战争策略优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.战争策略优化BP神经网络3.1 BP神经网络参数设置3.2 战争策略算法应用 4.测试结果…...
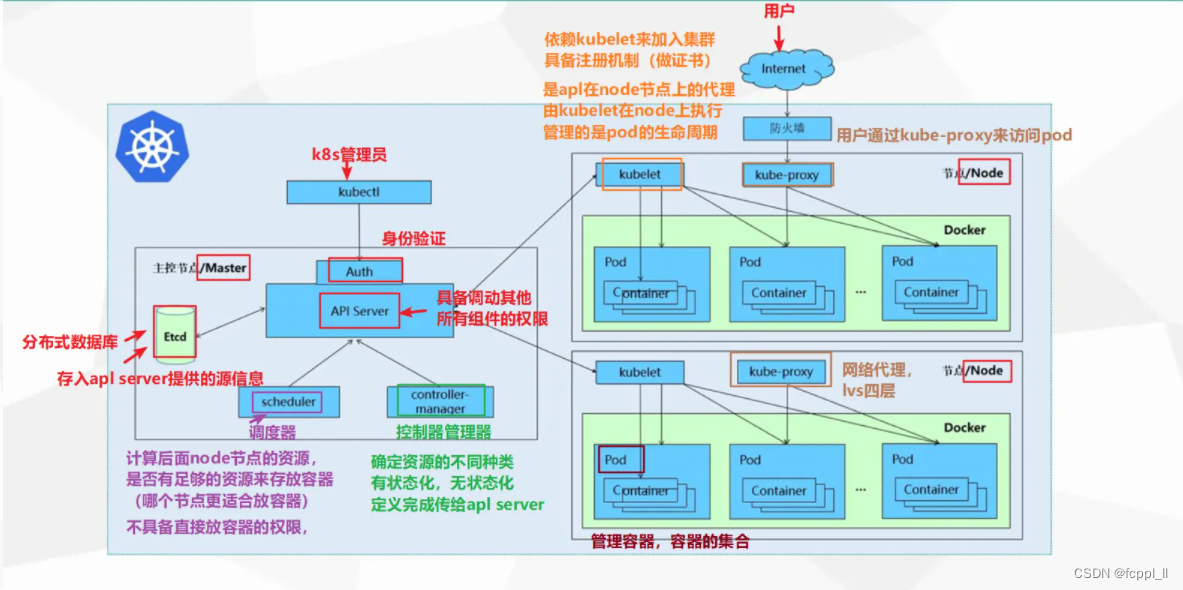
K8s 概念及组件
K8s 的全称为Kubernetes,是一种开源的容器编排平台,用于自动化部署以及扩展和管理容器化的应用程序,它提供了一种容器编排和管理的方式,可以帮助开发人员更轻松的管理容器化的应用程序,并且提供了一种跨多个主机的自动…...

【已解决】java的gradle项目报错org.gradle .api.plugins .MavenPlugin
我的java的gradle项目经常报错org.gradle .api.plugins .MavenPlugin。报错这个问题是因为依赖起冲突了,我在网上试了很多方法都没有效果,折让小编我很是苦恼,不过还好到最后问题还是解决了。 首先要知道你的项目所使用的gradle版本…...
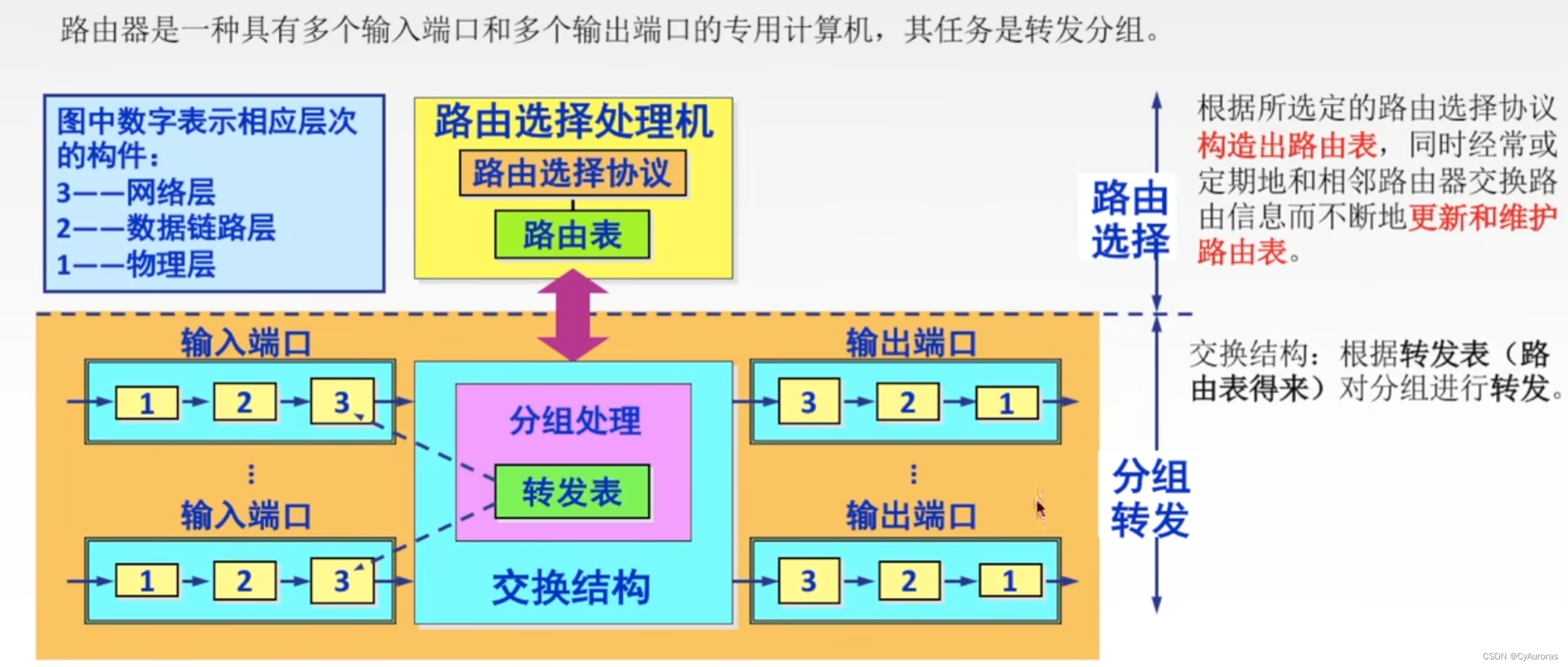
计算机网络-计算机网络体系结构-网络层
目录 一、IPV4 IP数据报格式 *IP 数据报分片 *IPV4地址 分类 网络地址转换(NAT) 二、子网划分与子网掩码 *CIDR *超网 协议 ARP协议 DHCP协议 ICMP协议 三、IPV6 格式 IPV4和IPV6区别 地址表示形式 四、路由选择协议 RIP(路由信息协议) OPSF(开发最短路径优…...

60 最长有效括号
最长有效括号 题目描述题解1 DPstack题解2 stack题解3 DP题解4 左右指针 题目描述 给你一个只包含 ( 和 ) 的字符串,找出最长有效(格式正确且连续)括号子串的长度。 示例 1: 输入:s "(()" 输出࿱…...
)
第17章 MQ(二)
17.11 RabbitMQ如何保证消息的顺序性 难度:★★ 重点:★★★ 白话解析 其实RabbitMQ是一个先进先出的队列,只要消息进入到队列之后那肯定是顺序的,其实这道题问的点就是在消息进队列之前和出队列之后如何保证顺序性。 1、要保证消息进队列的顺序性实际只需要保证生产者只…...

AV1 视频编码标准资源
AV1 视频编码标准资源 A Progress Report: The Alliance for Open Media and the AV1 Codec Alliance for Open Media(开放媒体联盟/AV1官网) aomanalyzer AOM ANALYZER TEST CLIPS(测试视频) (Download each of the the CIF clips found there, in YUV4MPEG (y4m) format…...
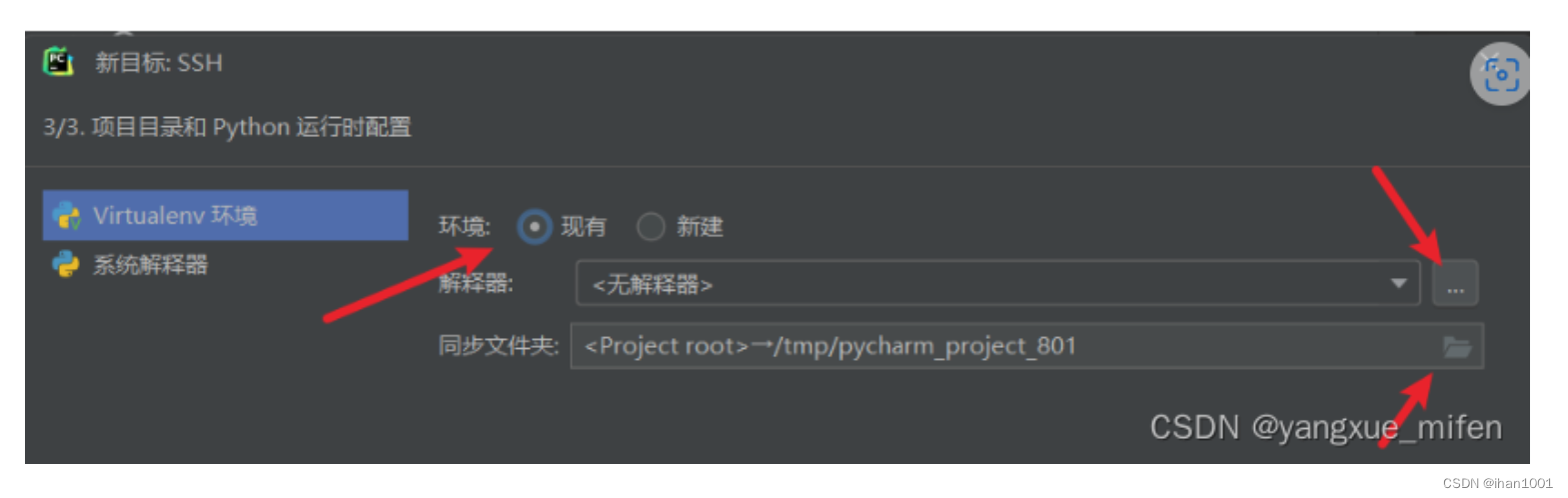
pycharm远程连接miniconda完整过程,以及遇到的问题解决
问题1:no-zero exit code(126) env: ‘/home/user2/miniconda3/envs/ihan/bin/python3’: Too many levels of symbolic links Python interpreter process exited with a non-zero exit code 126 因为选择的新建导致太多软连接,先在服务器上建好虚拟环…...
leetcode:2678. 老人的数目(python3解法)
难度:简单 给你一个下标从 0 开始的字符串 details 。details 中每个元素都是一位乘客的信息,信息用长度为 15 的字符串表示,表示方式如下: 前十个字符是乘客的手机号码。接下来的一个字符是乘客的性别。接下来两个字符是乘客的年…...

【马蹄集】—— 概率论专题:第二类斯特林数
概率论专题:第二类斯特林数 目录 MT2224 矩阵乘法MT2231 越狱MT2232 找朋友MT2233 盒子与球MT2234 点餐 MT2224 矩阵乘法 难度:黄金 时间限制:5秒 占用内存:128M 题目描述 输入两个矩阵,第一个矩阵尺寸为 l…...

spring中基础核心接口总结
理解这几个接口,及其实现类就可以快速了解spring,具体的用法参考其他spring资料 1.BeanFactory最基础最核心的接口 重要的实现类有:XmlBeanFactory,以及ApplicationContext接口下的类 2.Resource接口,可以通用地访问文件资源 1)ClassPathResource:读取…...

最新Tuxera NTFS2024破解版mac读写NTFS磁盘工具
Tuxera NTFS for Mac是一款Mac系统NTFS磁盘读写软件。在系统默认状态下,MacOSX只能实现对NTFS的读取功能,Tuxera NTFS可以帮助MacOS 系统的电脑顺利实现对NTFS分区的读/写功能。Tuxera NTFS 2024完美兼容最新版本的MacOS 11 Big Sur,在M1芯片…...
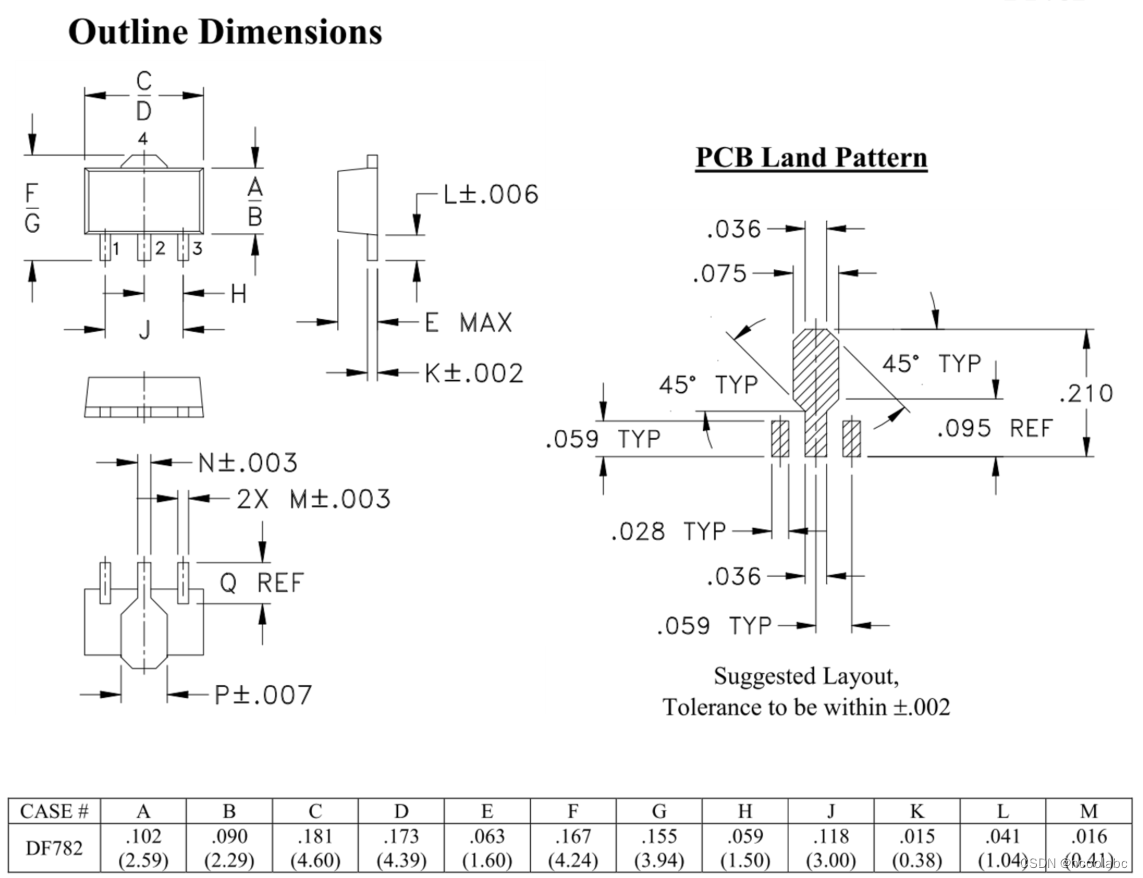
【标准化封装 SOT系列 】 E SOT-89
〇、SOT-89 这个封装也比较常见,但并不易错。 一、E部分 SOT-89 参数 pin-pin 间距1.5mm body size 4.52.5 二、符合当前标准的典型举例 名称pin 数厂家 body DE矩形 (mm)SOT-894Mini-Circuits – PGA-102 — 4.39/4.62.29/2.59 上图 MiniCircuits 也称DF78…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
