60 最长有效括号
最长有效括号
- 题目描述
- 题解1 DP+stack
- 题解2 stack
- 题解3 DP
- 题解4 左右指针
题目描述
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"示例 3:
输入:s = ""
输出:0
题解1 DP+stack
class Solution {
public:int longestValidParentheses(string s) {int st = s.size();if(0 == st) return 0;stack<int> stk;vector<int> dp(st+1, 0);for(int i = 0; i < st; i++){if(s[i] == '('){stk.push(i);// 如果是左括号说明i位置不会有效,对应在dp里i+1位置置零即可dp[i+1] = 0;}else{if(! stk.empty()){// 如果没有stack,递推公式稍微复杂一点// key:别忘了+dp[stk.top()]// 以防迷惑:stk.top()是最近的左括号下标值,dp[stk.top()+1]=0dp[i+1] = i + 1 - stk.top() + dp[stk.top()];stk.pop(); }else dp[i+1] = 0;}}int ret = INT_MIN;for(auto& i : dp){ret = max(ret, i);}return ret;}
};

题解2 stack
class Solution {
public:int longestValidParentheses(string s) {int st = s.size();if(0 == st) return 0;stack<int> stk;// 处理第一个字符是左括号的情况stk.push(-1);int ret = 0;for(int i = 0; i < st; i++){if(s[i] == '('){stk.push(i);}else{// 遇到右括号,先弹栈(遇到右括号,前面的连续有效括号就作废了)stk.pop();if(! stk.empty()){ret = max(ret, i-stk.top());}else {stk.push(i);}}}return ret;}
};

题解3 DP
class Solution {
public:int longestValidParentheses(string s) {int st = s.size();if(0 == st) return 0;vector<int> dp(st, 0);int maxS = 0; for(int i = 1; i < st; i++){if(s[i] == ')'){// "()()"if(s[i-1] == '('){dp[i] = 2;// 前面还有项(如果有stack就会马上定位到上一个有效序列的开始)if(i >= 2)dp[i] = dp[i-2] + dp[i];}// "(())"else if(dp[i-1]){if(i-1-dp[i-1] >= 0 && s[i-1-dp[i-1]] == '('){dp[i] = dp[i-1] + 2;// 前面还有项if(i - dp[i-1] - 2 >= 0)dp[i] = dp[i] + dp[i - dp[i - 1] - 2];} } }maxS = max(maxS, dp[i]);}return maxS;}
};

题解4 左右指针
class Solution {
public:int longestValidParentheses(string s) {int left = 0, right = 0, maxlength = 0;// 左扫for (int i = 0; i < s.length(); i++) {if (s[i] == '(') {left++;} else {right++;}if (left == right) {maxlength = max(maxlength, 2 * right);} else if (right > left) {left = right = 0;}}left = right = 0;// 右扫:解决左扫扫不出来的"(((()"for (int i = (int)s.length() - 1; i >= 0; i--) {if (s[i] == '(') {left++;} else {right++;}if (left == right) {maxlength = max(maxlength, 2 * left);} else if (left > right) {left = right = 0;}}return maxlength;}
};

相关文章:

60 最长有效括号
最长有效括号 题目描述题解1 DPstack题解2 stack题解3 DP题解4 左右指针 题目描述 给你一个只包含 ( 和 ) 的字符串,找出最长有效(格式正确且连续)括号子串的长度。 示例 1: 输入:s "(()" 输出࿱…...
)
第17章 MQ(二)
17.11 RabbitMQ如何保证消息的顺序性 难度:★★ 重点:★★★ 白话解析 其实RabbitMQ是一个先进先出的队列,只要消息进入到队列之后那肯定是顺序的,其实这道题问的点就是在消息进队列之前和出队列之后如何保证顺序性。 1、要保证消息进队列的顺序性实际只需要保证生产者只…...

AV1 视频编码标准资源
AV1 视频编码标准资源 A Progress Report: The Alliance for Open Media and the AV1 Codec Alliance for Open Media(开放媒体联盟/AV1官网) aomanalyzer AOM ANALYZER TEST CLIPS(测试视频) (Download each of the the CIF clips found there, in YUV4MPEG (y4m) format…...
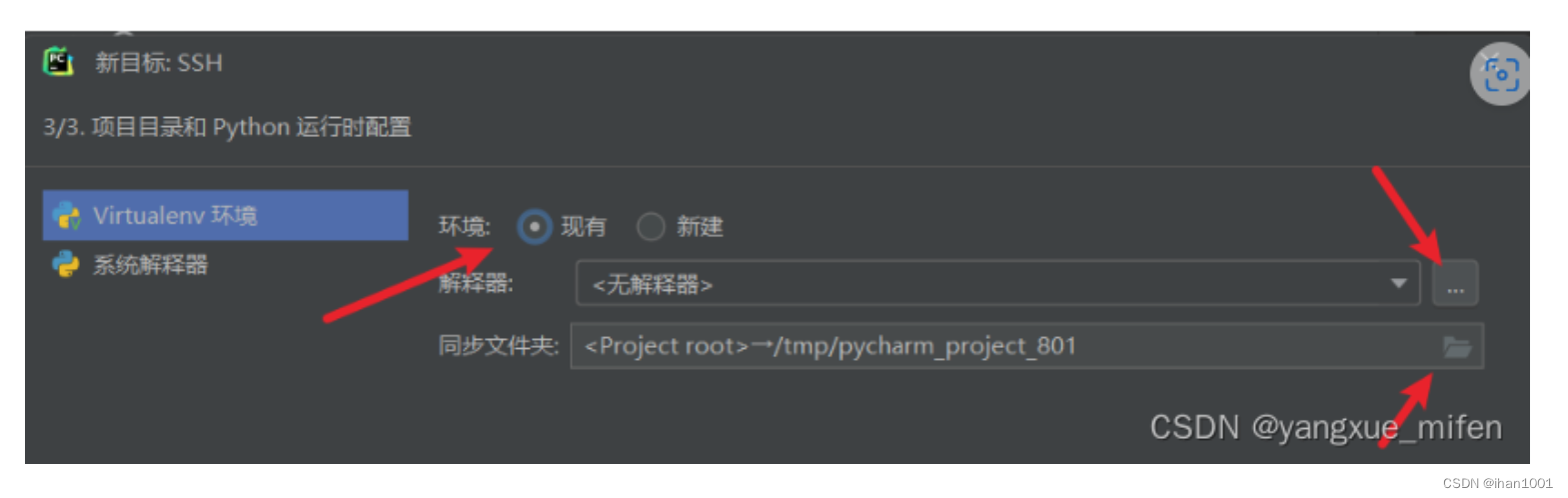
pycharm远程连接miniconda完整过程,以及遇到的问题解决
问题1:no-zero exit code(126) env: ‘/home/user2/miniconda3/envs/ihan/bin/python3’: Too many levels of symbolic links Python interpreter process exited with a non-zero exit code 126 因为选择的新建导致太多软连接,先在服务器上建好虚拟环…...
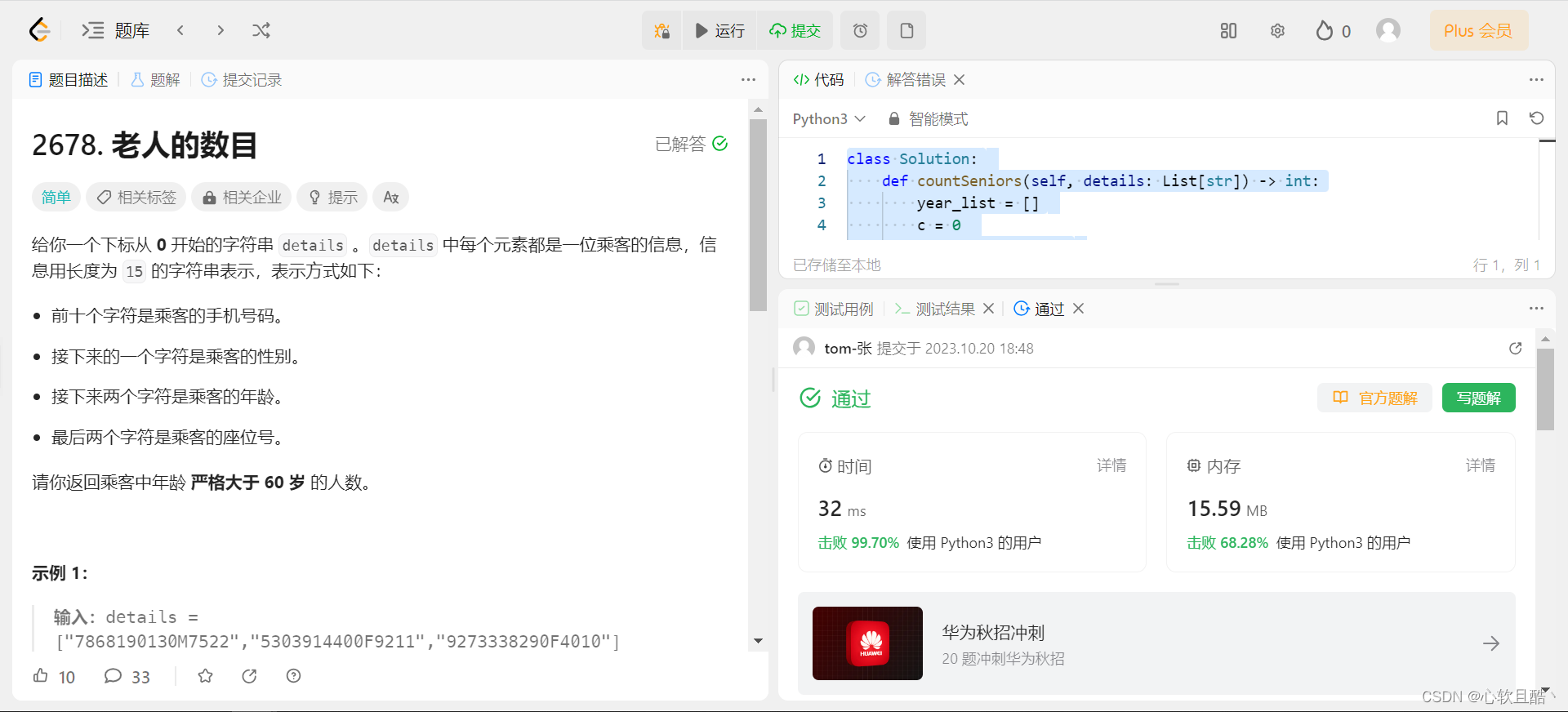
leetcode:2678. 老人的数目(python3解法)
难度:简单 给你一个下标从 0 开始的字符串 details 。details 中每个元素都是一位乘客的信息,信息用长度为 15 的字符串表示,表示方式如下: 前十个字符是乘客的手机号码。接下来的一个字符是乘客的性别。接下来两个字符是乘客的年…...

【马蹄集】—— 概率论专题:第二类斯特林数
概率论专题:第二类斯特林数 目录 MT2224 矩阵乘法MT2231 越狱MT2232 找朋友MT2233 盒子与球MT2234 点餐 MT2224 矩阵乘法 难度:黄金 时间限制:5秒 占用内存:128M 题目描述 输入两个矩阵,第一个矩阵尺寸为 l…...

spring中基础核心接口总结
理解这几个接口,及其实现类就可以快速了解spring,具体的用法参考其他spring资料 1.BeanFactory最基础最核心的接口 重要的实现类有:XmlBeanFactory,以及ApplicationContext接口下的类 2.Resource接口,可以通用地访问文件资源 1)ClassPathResource:读取…...

最新Tuxera NTFS2024破解版mac读写NTFS磁盘工具
Tuxera NTFS for Mac是一款Mac系统NTFS磁盘读写软件。在系统默认状态下,MacOSX只能实现对NTFS的读取功能,Tuxera NTFS可以帮助MacOS 系统的电脑顺利实现对NTFS分区的读/写功能。Tuxera NTFS 2024完美兼容最新版本的MacOS 11 Big Sur,在M1芯片…...
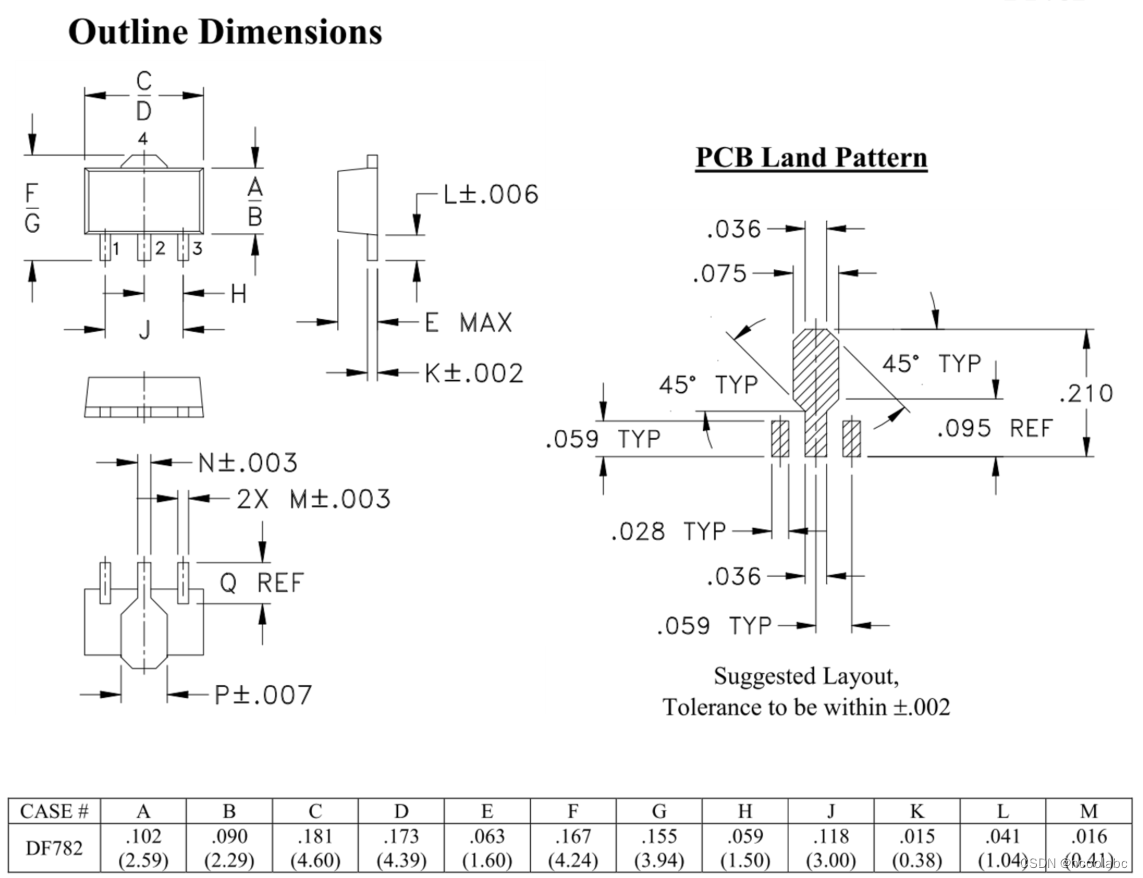
【标准化封装 SOT系列 】 E SOT-89
〇、SOT-89 这个封装也比较常见,但并不易错。 一、E部分 SOT-89 参数 pin-pin 间距1.5mm body size 4.52.5 二、符合当前标准的典型举例 名称pin 数厂家 body DE矩形 (mm)SOT-894Mini-Circuits – PGA-102 — 4.39/4.62.29/2.59 上图 MiniCircuits 也称DF78…...
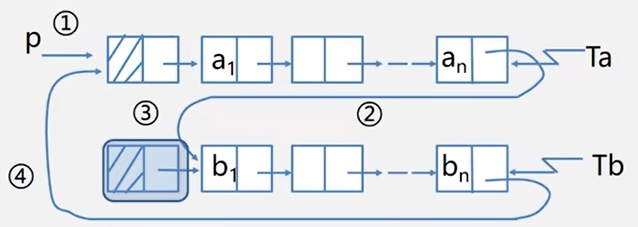
【建立单链表:头插法,尾插法;循环列表,带尾指针的循环链表合并(将Tb合并在Ta之后)】
文章目录 一、单链表的基本操作的实现1.建立单链表:头插法----元素插入在链表头部,也叫头插法。2.建立单链表:尾插法----元素插入在链表尾部,也叫尾插法。 二、线性表的链式表示和实现1.循环列表2.带尾指针的循环链表合并…...

图论+线性基高斯消元与主元:1019T2 / P4151
http://cplusoj.com/d/senior/p/SS231019B 相当于图上选一条链和一堆环 考虑dfs生成树。 则链是两条从根出发的链 环是每条返祖边组成的环 所以环和链的异或和可以求出来 链的放到线性基里 然后线性基通过高斯消元求主元(贪心思想,主元可以令那一位…...

Django REST Framework完整教程-RESTful规范-序列化和反序列数据-数据视图
文章目录 1.简介及安装2.案例模型2.1.创建模型2.2.安装mysql必要组件2.3.管理后台转中文2.4.启动后台 3.数据序列化4.RESTful规范4.1.协议、域名和版本4.2.uri(统一资源标识符)4.3.查增删改4.4.过滤信息(Filtering)4.5.状态码(Status Codes&a…...

float、double类型的转化和判断为零问题
1、将字符串转化为float、double 浮点数在内存中的存储机制和整形数据不同,有舍入误差,在计算机中用近似表示任意某个实数。具体来说,这个数由一个整数或定点数(即尾数)乘以某个基数(计算机中通常是2&…...
强大的虚拟机软件 VMware Fusion Pro 13中文最新 for mac
VMware Fusion Pro是一款虚拟化软件,它允许在Mac电脑上同时运行Windows和其他操作系统,而无需重启电脑,它采用了领先的虚拟化技术,能够保证在Mac电脑在同时运行多个操作系统时表现出极高的效率和稳定性。 VMware Fusion Pro具有以…...
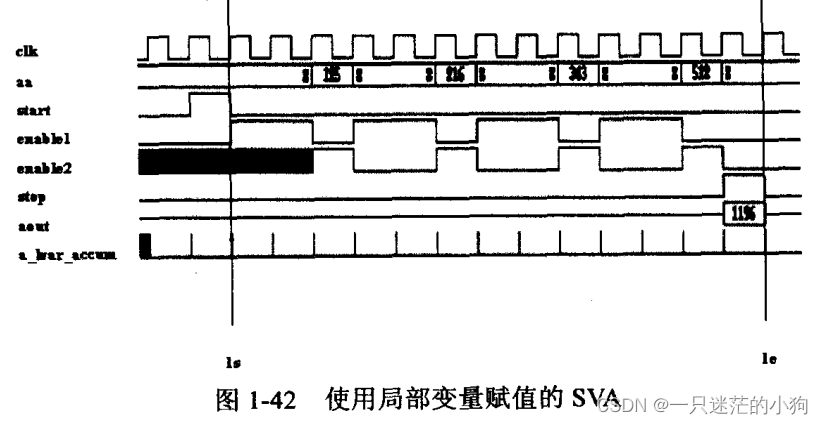
SystemVerilog Assertions应用指南 Chapter1.37 使用局部变量的SVA
在序列或者属性的内部可以局部定义变量,而且可以对这种变量进行赋值。变量接着子序列放置,用逗号隔开。如果子序列匹配,那么变量赋值语句执行。每次序列被尝试匹配时,会产生变量的一个新的备份。 module cubed(enable1, a, aa, clk);input logic [7:0] a; input logic enable1,…...

Linux实现无需手动输入密码的自动化SSH身份验证
SSH密钥身份验证是一种安全的方式,使您能够在无需手动输入密码的情况下连接到远程服务器。以下是如何设置SSH密钥身份验证,以便您的脚本能够自动运行: 步骤 生成SSH密钥对: 在您的本地系统上生成SSH密钥对。如果您尚未生成,请使用…...

CSS 效果 圆形里一个文字居中
效果实现源码: 宽度,高度必须确认,且相等 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><style>.circlew {width: 45px;height: 45p…...
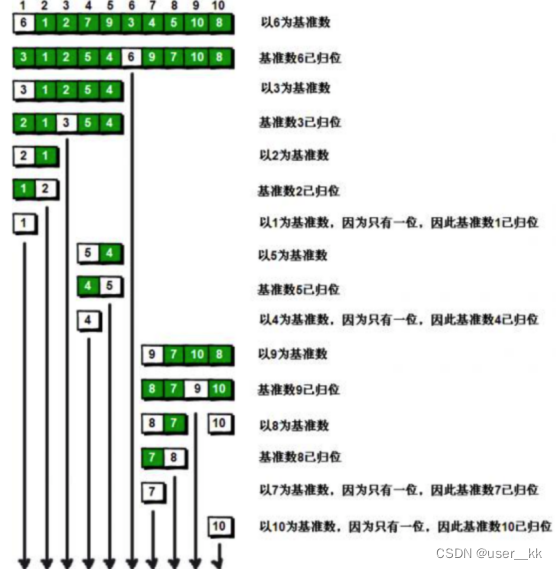
排序算法,冒泡排序算法及优化,选择排序SelectionSort,快速排序(递归-分区)
一、冒泡排序算法: 介绍: 冒泡排序(Bubble Sort)是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需…...

编写内联函数求解 2x²+4x+5的值,并用主函数调用该函数
动态内存分配可以根据实际需要在程序运行过程中动态地申请内存空间,这种内存空间的分配和释放是由程序员自己管理的,因此也被称为手动内存分配。 C++ 中,动态内存的分配和释放是通过 new 和 delete 操作符进行的。new 操作符用于在堆内存上为对象动态分配空间,dele…...
【Release】Photoshop ICO file format plug-in 3.0
【Introduction】 The Photoshop ICO plug-in is a file format plug-in developed for Photoshop, which allows Photoshop to directly read and write ICO format files. Because Photoshop has powerful pixel bitmap editing functions, it has many users and a good us…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
