图论+线性基高斯消元与主元:1019T2 / P4151
http://cplusoj.com/d/senior/p/SS231019B
相当于图上选一条链和一堆环
考虑dfs生成树。
则链是两条从根出发的链
环是每条返祖边组成的环
所以环和链的异或和可以求出来
链的放到线性基里
然后线性基通过高斯消元求主元(贪心思想,主元可以令那一位一定为1。那么就钦定主元为必选,这样一定更优)
高消的过程中也需要对链进行消元
最后用链来查询,丢01trie上维护
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 100010
//#define M
//#define mo
int n, m, i, j, k, T;
int ans, C, MY, dis[N];
struct line_kun {int p[100]; void push(int k) {
// printf("Add %lld\n", k); for(int j = 62; j >= 0; --j)if((k>>j)&1) {if(!p[j]) { p[j]=k; break; }k^=p[j]; }}void xiaoyuan() {
// for(int j = 62; j >= 0; --j) printf("%lld ", p[j]); printf("\n"); for(int j = 62; j >= 0; --j)if(p[j]) {for(int i = 62; i > j; --i) if((p[i]>>j)&1) p[i]^=p[j]; for(int i = 1; i <= n; ++i) if((dis[i]>>j)&1) dis[i]^=p[j]; }
// for(int j = 62; j >= 0; --j) printf("%lld ", p[j]); printf("\n"); }pair<int, int> main_Y() {int k = (1ll<<62)-1, ans = 0; for(int j = 62; j >= 0; --j) if(p[j]) k-=(1ll<<j), ans^=p[j]; return {k, ans}; }
}J;
struct Trie_tree {int tot = 1, son[N * 60][2] ; int que_max(int x) {
// printf("Que_mx : %lld\n", x); int u = 1, i, k, ans=0; for(i = 62; i>=0; --i) {k = (x>>i)&1ll; if(son[u][k^1]) u=son[u][k^1], ans|=((k^1)<<i); else u=son[u][k], ans|=(k<<i); }
// printf("\t We get %lld\n", ans); return ans; }void add(int x) {int u = 1, i, k; for(i = 62; i >= 0; --i) {k = (x>>i)&1ll; if(!son[u][k]) son[u][k] = ++tot; u = son[u][k]; }}
}Trie;
struct node {int y, z;
};
int u, v, w;
pair<int, int>p;
vector<node>G[N]; void dfs(int x, int fa) {for(auto t : G[x]) {int y = t.y, z = t.z;
// if(t.y == fa) continue; if(dis[y] == -1) {dis[y] = dis[x] ^ z; dfs(y, x); }else J.push(dis[x] ^ dis[y] ^ z); }
}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// freopen("path.in", "r", stdin);
// freopen("path.out", "w", stdout);
T=read();
// while(T--) {
//
// }n = read(); m = read(); for(i=1; i<=m; ++i) {u = read(); v = read(); w = read(); G[u].pb({v, w}); G[v].pb({u, w}); }memset(dis, -1, sizeof(dis)); dis[1]=0; dfs(1, 0);
// for(i=1; i<=n; ++i) printf("%lld ", dis[i]); printf("\n"); J.xiaoyuan(); p = J.main_Y(); MY = p.first; C = p.second;
// cout<<(bitset<100>)(MY)<<endl;
// for(i=1; i<=n; ++i) dis[i]&=MY;
// printf("# %lld %lld %lld\n", MY, C, k); k=C-(MY&C); C&=MY;
// printf("# %lld %lld %lld\n", MY, C, k);
// for(i=1; i<=n; ++i) printf("%lld ", dis[i]); printf("\n"); Trie.add(0); for(i=1; i<=n; ++i) {if(i==1) Trie.add(dis[i]); if(i==n) ans = max(ans, dis[i]^Trie.que_max(dis[i]^C)^C); }printf("%lld", ans^k); return 0;
}相关文章:

图论+线性基高斯消元与主元:1019T2 / P4151
http://cplusoj.com/d/senior/p/SS231019B 相当于图上选一条链和一堆环 考虑dfs生成树。 则链是两条从根出发的链 环是每条返祖边组成的环 所以环和链的异或和可以求出来 链的放到线性基里 然后线性基通过高斯消元求主元(贪心思想,主元可以令那一位…...

Django REST Framework完整教程-RESTful规范-序列化和反序列数据-数据视图
文章目录 1.简介及安装2.案例模型2.1.创建模型2.2.安装mysql必要组件2.3.管理后台转中文2.4.启动后台 3.数据序列化4.RESTful规范4.1.协议、域名和版本4.2.uri(统一资源标识符)4.3.查增删改4.4.过滤信息(Filtering)4.5.状态码(Status Codes&a…...

float、double类型的转化和判断为零问题
1、将字符串转化为float、double 浮点数在内存中的存储机制和整形数据不同,有舍入误差,在计算机中用近似表示任意某个实数。具体来说,这个数由一个整数或定点数(即尾数)乘以某个基数(计算机中通常是2&…...
强大的虚拟机软件 VMware Fusion Pro 13中文最新 for mac
VMware Fusion Pro是一款虚拟化软件,它允许在Mac电脑上同时运行Windows和其他操作系统,而无需重启电脑,它采用了领先的虚拟化技术,能够保证在Mac电脑在同时运行多个操作系统时表现出极高的效率和稳定性。 VMware Fusion Pro具有以…...
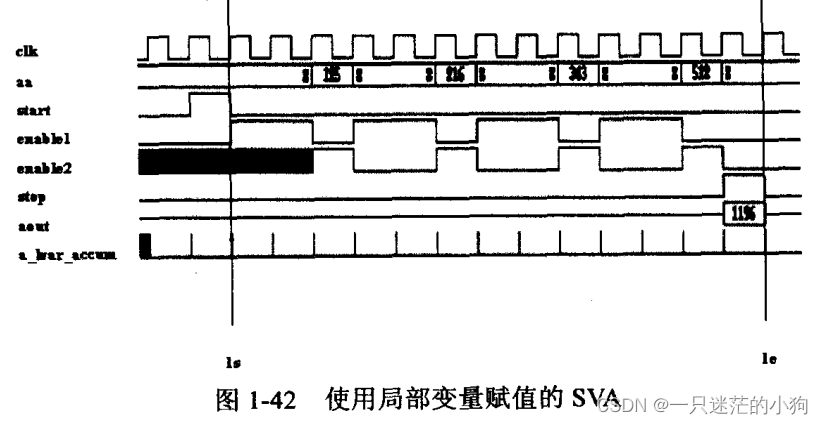
SystemVerilog Assertions应用指南 Chapter1.37 使用局部变量的SVA
在序列或者属性的内部可以局部定义变量,而且可以对这种变量进行赋值。变量接着子序列放置,用逗号隔开。如果子序列匹配,那么变量赋值语句执行。每次序列被尝试匹配时,会产生变量的一个新的备份。 module cubed(enable1, a, aa, clk);input logic [7:0] a; input logic enable1,…...

Linux实现无需手动输入密码的自动化SSH身份验证
SSH密钥身份验证是一种安全的方式,使您能够在无需手动输入密码的情况下连接到远程服务器。以下是如何设置SSH密钥身份验证,以便您的脚本能够自动运行: 步骤 生成SSH密钥对: 在您的本地系统上生成SSH密钥对。如果您尚未生成,请使用…...

CSS 效果 圆形里一个文字居中
效果实现源码: 宽度,高度必须确认,且相等 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><style>.circlew {width: 45px;height: 45p…...
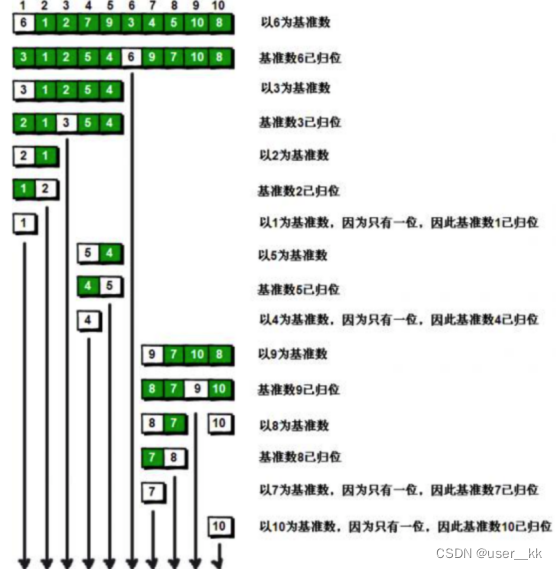
排序算法,冒泡排序算法及优化,选择排序SelectionSort,快速排序(递归-分区)
一、冒泡排序算法: 介绍: 冒泡排序(Bubble Sort)是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需…...

编写内联函数求解 2x²+4x+5的值,并用主函数调用该函数
动态内存分配可以根据实际需要在程序运行过程中动态地申请内存空间,这种内存空间的分配和释放是由程序员自己管理的,因此也被称为手动内存分配。 C++ 中,动态内存的分配和释放是通过 new 和 delete 操作符进行的。new 操作符用于在堆内存上为对象动态分配空间,dele…...
【Release】Photoshop ICO file format plug-in 3.0
【Introduction】 The Photoshop ICO plug-in is a file format plug-in developed for Photoshop, which allows Photoshop to directly read and write ICO format files. Because Photoshop has powerful pixel bitmap editing functions, it has many users and a good us…...

List.of() Vs Arrays.asList()
java中list.of和Arrays.asList方法有什么区别? 简介 Java 提供了几种用于创建列表的方便方法,包括 List.of 和 Arrays.aslist。尽管这两种方法都可以很简单的创建集合对象,但它们实际上是有一些显著差异的。本文将介绍 Java 中的 List.of()…...

机器学习-计算数据之间的距离
目录 欧氏距离 欧氏距离应用场景: 聚类分析:在聚类算法中(K-means)中,可以使用欧式距离来衡量数据点之间的相似性或距离,以便于将他们划分到不用的簇中。特征匹配:在计算机视觉和图像处理中,可以使用欧氏…...
Uniapp软件库源码 全新带勋章功能(包含前后端源码)
Uniapp软件库全新带勋章功能,搭建好后台 在前端找到 util 这个文件 把两个js文件上面的填上自己的域名, 电脑需要下载:HBuilderX 登录账号 没有账号就注册账号,然后上传文件,打包选择 “发行” 可以打包app h5等等。…...
陪诊小程序|陪诊小程序关爱健康,无忧陪伴
随着社会发展和人们生活水平的提高,健康问题成为人们关注的焦点。然而,在就医过程中,许多患者常常感到孤独和无助,缺乏得到家人陪伴的温暖与安慰。为了解决这一问题,我们公司开发了一款创新的陪诊小程序软件࿰…...
uni-app小程序使用DCloud(插件市场)流程
一、DCloud(插件市场) DCloud 是uni-app官方插件市场,里面有官方、团队、个人发布的众多插件,包括uni-ui、uni-pay 等。而像uni-ui这种大型组件库都有官方文档可参考,但一些团队或个人发布的小型插件没有文档…...
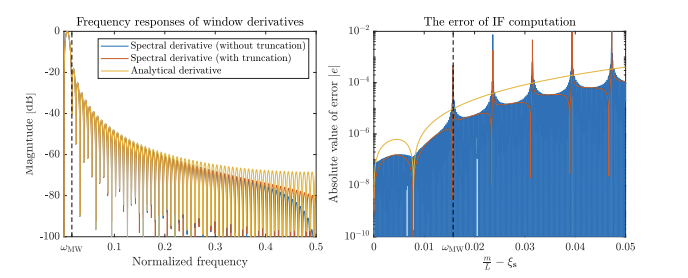
非平稳信号分析和处理、STFT的瞬时频率研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

SIPp使用经验
xml文件,建议<?xml version"1.0" encoding"UTF-8" ?>,不建议ISO-8859-1命令行传key参数 sipp -key contact_port 9999 ...<send retrans"500"><![CDATA[REGISTER sip:[field1]:[remote_port] SIP/2.0Vi…...
ChessGPT:免费好用的国际象棋对弈AI机器人
对于国际象棋初学者,需要找一个对手来练棋。ChessGPT,就是一个免费好用的AI对弈机器人,非常适合新手来提升,是一个很好的练习伙伴。网站地址是:https://www.chess.com/play/computer,也有手机版app…...
【java】A卷+B卷)
华为OD 区间交集(200分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...
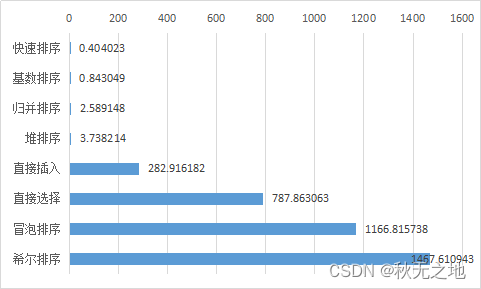
Python算法:八大排序算法以及速度比较
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
