机器学习-计算数据之间的距离
目录
欧氏距离
欧氏距离应用场景:
- 聚类分析:在聚类算法中(K-means)中,可以使用欧式距离来衡量数据点之间的相似性或距离,以便于将他们划分到不用的簇中。
- 特征匹配:在计算机视觉和图像处理中,可以使用欧氏距离来比较两个特征向量之间的相似性,如图像检索,图像分类,人脸识别等任务。
- 数据降维:在主成分分析(PCA)和线性判别分析(LDA)等降维技术中,可以使用欧氏距离来衡量高维数据空间中的变量之间的相似性,从而进行有效的特征选择和降维。
- 推荐系统:在协同过滤推荐算法中,可以使用欧氏距离来衡量用户之间的兴趣相似性,从而根据用户的历史行为向其推荐相似的物品或内容。
- 数据挖掘:在聚类,分类和异常检测层数据挖掘任务中,可以使用欧氏距离来度量数据点之间的差异和相似性,以便进行模式识别和异常检测。
大多数情况欧式距离都是比较适合的。但是对于某些特殊类型的
欧氏距离是最常见的距离度量方法,它定义为两个点之间的直线距离。对于两个n维向量X和Y,欧氏距离可以表示为: d ( x , y ) = ( ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ + ( x n − y n ) 2 ) d(x,y)=\sqrt((x_1-y_1)^2+(x_2-y_2)^2+······+(x_n-y_n)^2) d(x,y)=((x1−y1)2+(x2−y2)2+⋅⋅⋅⋅⋅⋅+(xn−yn)2)
代码实现:
import numpy as np
from scipy.spatial.distance import cdist# 示例数据
data = np.array([[1, 2, 3], [4, 5, 6]])# 计算欧氏距离矩阵
distance_matrix = cdist(data, data, metric='euclidean')print("欧氏距离矩阵:\n", distance_matrix)这里使用了scipy包中的的cdist。
也可以进行自定义:
import numpy as npdef euclidean_distance(x,y):x = np.array(x)y = np.array(y)distance = np.sqrt(np.sum(np.square(x-y))return distance
data1 = [1,2,3]
data2 = [4,5,6]
distance = euclidean_distance(data1,data2)
曼哈顿距离
曼哈顿距离主要应用场景:
-
路径规划和导航:在特定的城市区域或地图上,可以使用曼哈顿距离来估计两点之间的实际行驶距离或路程,从而确定最短路径或导航方案。
-
电子商务:在购物网站或电子商务平台上,可以使用曼哈顿距离来衡量产品或服务之间的相似性,从而向用户推荐相关的商品或服务。
-
计算机视觉:在图像处理和计算机视觉领域中,可以使用曼哈顿距离来比较两个图像之间的相似性或距离,例如在文本检测和OCR(光学字符识别)中使用。
-
数据挖掘:在聚类、分类和异常检测等数据挖掘任务中,可以使用曼哈顿距离来度量数据点之间的差异和相似性,以便进行模式识别和异常检测。
-
传感器网络:在传感器网络中,可以使用曼哈顿距离来估计物理位置或传感器之间的距离,从而实现位置估计和目标跟踪等任务。
曼哈顿距离是在城市街区中的距离度量方法,它表示两点之间沿着坐标轴的总距离。
曼哈顿距离采用各个坐标点之间的绝对值之和,它的距离定义为:
d ( x , y ) = ∣ x 1 − y 1 ∣ + ∣ x 2 − y 2 ∣ + ⋅ ⋅ ⋅ + ∣ x n − y n ∣ d(x,y)=|x_1-y_1|+|x_2-y_2|+···+|x_n-y_n| d(x,y)=∣x1−y1∣+∣x2−y2∣+⋅⋅⋅+∣xn−yn∣
自定义曼哈顿距离
import numpy as npdef manhattan_distance(x,y):x = np.array(x)y = np.array(y)distance = np.sum(np.abs(x-y))return distance
data1 = [1,2,3]
data2 = [4,5,6]
distance = manhattan_distance(data1,data2)
使用cdist库来进行实现
distance.cdist(x,x,"cityblock")
闵可夫斯基距离
闵可夫斯基距离是欧氏距离和曼哈顿距离的一般化形式,可以表示为:$ d ( x , y ) = ( ∣ x 1 − y 1 ∣ p + ∣ x 2 − y 2 ∣ p + . . . + ∣ x n − y n ∣ p ) ( 1 / p ) d(x, y) = (|x1 - y1|^p + |x2 - y2|^p + ... + |xn - yn|^p)^{(1/p)} d(x,y)=(∣x1−y1∣p+∣x2−y2∣p+...+∣xn−yn∣p)(1/p),其中p为正实数。
import numpy as npdef minkowski_distance(x,y):x = np.array(x)y = np.array(y)distance = np.power(np.sum(np,power(np.abs(x-y), p)),1/p)return distancedata1 = [1,2,3]
data2 = [4,5,6]
p = 2 # 欧氏距离’
distance=minkowski_distance(data1,data2,p)
使用cdist库来实现
from scipy.spatial.distance import cdist# 示例数据
data1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
data2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
p = 2 # 欧氏距离# 使用cdist计算闵可夫斯基距离
distance_matrix = cdist(data1, data2, metric='minkowski', p=p)print("距离矩阵:")
print(distance_matrix)切比雪夫距离
切比雪夫距离是在棋盘格上的距离度量方法,它表示两点之间坐标数值差的最大值。
切比雪夫距离是指两个点之间各个坐标数值差绝对值的最大值,定义为:
d ( x , y ) = m a x i ( ∣ x i − y i ∣ ) d(x,y)=max_i(|x_i-y_i|) d(x,y)=maxi(∣xi−yi∣)
import numpy as np
def chebyshev_distance(x,y):x = np.array(x)y = np.array(y)distance = np.max(np.abs(x-y))return distance
data1 = [1,2,3]
data2 = [4,5,6]
distance = chebyshev_distance(data1,data2)
使用cdist库来实现
distance.cdist(x,x,"chebyshev")
余弦距离
余弦距离通常用于计算文本和稀疏数据之间的相似度。余弦相似度度量的是两个向量之间的角度关系,而不是其具体数值大小。余弦相似度定义为两个向量的内积除以它们的模长乘积。
余弦距离是通过测量两个向量夹角来进行度量两个向量之间的相似性,余弦距离定义为:
d ( x , y ) = x ∗ y ∑ x i 2 ∗ ∑ y i 2 d(x,y)=\frac{x*y}{\sqrt{ \sum x_i^2}*\sqrt{\sum y_i^2}} d(x,y)=∑xi2∗∑yi2x∗y
import numpy as np
def cosine_distance(x, y):x = np.array(x)y = np.array(y)# 计算向量的内积dot_product = np.dot(x, y)# 计算向量的模长norm_x = np.linalg.norm(x)norm_y = np.linalg.norm(y)# 计算余弦距离distance = 1-(dot_product / (norm_x * norm_y))return distancedata1=[1,2,3]
data2=[4,5,6]
distance = cosine_distance(data1,data2)
使用cdist库实现
distance.cdist(x,x,"cosine")
相关系数距离
相关系数距离主要用于衡量个两个变量之间的相关性或者相似度。它可以用来比较两个向量,时间序列或者数据集之间的相似程度,如下场景可能会用到:
- 数据分析和统计学:相关系数距离可用于评估不同变量之间之间的相关性,在数据分析和统计学中,我们可以使用相关系数距离来确定两个变量之间的线性关系强弱。
- 机器学习和数据挖掘:在特征选择,聚类,回归和分类等机器学习任务中,相关系数距离可以用作相似性度量。例如在聚类算法中,可以使用相关系数距离来测量数据点之间的相似程度,进而将相似的数据点分组。
- 图像处理和计算机视觉:相关系数距离可以用于图像匹配和相似性比较。通过计算连个图像之间的相关系数距离,来评估他们之间的相似度,用于图像检索,目标识别和图形匹配等应用。
- 自然语言处理和文本挖掘:在文本分析领域,相关数据里可以用于比较文本之间的相似性。通过计算文本之间的相关系数距离,可以进行文本聚类,文档相似度计算和信息检索等任务。
相关系数距离只能测量线性关系的相似性,对于非线性关系的判断不太准确。
定义为:
d ( x , y ) = ( x − x ˉ ) ∗ ( y − y ˉ ) ∑ x i − X ˉ ∗ ∑ y i − Y ˉ d(x,y)=\frac{(x-\bar x)*(y-\bar y)}{\sqrt{\sum x_i-\bar X}*\sqrt{\sum y_i -\bar Y}} d(x,y)=∑xi−Xˉ∗∑yi−Yˉ(x−xˉ)∗(y−yˉ)
import math# 示例数据
vector1 = [1, 2, 3]
vector2 = [4, 5, 6]# 计算平均值
mean1 = sum(vector1) / len(vector1)
mean2 = sum(vector2) / len(vector2)# 计算标准差
std1 = math.sqrt(sum((x - mean1) ** 2 for x in vector1) / len(vector1))
std2 = math.sqrt(sum((x - mean2) ** 2 for x in vector2) / len(vector2))# 计算协方差
covariance = sum((x - mean1) * (y - mean2) for x, y in zip(vector1, vector2)) / len(vector1)# 计算相关系数距离
correlation_distance = 1 - (covariance / (std1 * std2))print("相关系数距离:", correlation_distance)使用库函数来进行实现:
# 二维以上因为cdist中的参数是向量,
distance.cdist(x,x,"correlation")
# 或者使用numpy中的corrcoef库
data1 = [1,2,3]
data2 = [4,5,6]
# 计算相关系数
correlation_coefficient = np.corrcoef(data1, data2)[0,1]
# 计算相关系数距离
correlation_distance = 1-correlation_coefficient
马氏距离
马氏距离表示数据的协方差距离,是一种计算两个未知样本集的相似度的有效方法,距离定义为:
d ( x , y ) = ( X − Y ) T ∑ − 1 ( X − Y ) d(x,y)=\sqrt{(X-Y)^T\sum ^{-1}(X-Y)} d(x,y)=(X−Y)T∑−1(X−Y)
distance.cdist(x,x,"mahalanobis")
相关文章:

机器学习-计算数据之间的距离
目录 欧氏距离 欧氏距离应用场景: 聚类分析:在聚类算法中(K-means)中,可以使用欧式距离来衡量数据点之间的相似性或距离,以便于将他们划分到不用的簇中。特征匹配:在计算机视觉和图像处理中,可以使用欧氏…...
Uniapp软件库源码 全新带勋章功能(包含前后端源码)
Uniapp软件库全新带勋章功能,搭建好后台 在前端找到 util 这个文件 把两个js文件上面的填上自己的域名, 电脑需要下载:HBuilderX 登录账号 没有账号就注册账号,然后上传文件,打包选择 “发行” 可以打包app h5等等。…...
陪诊小程序|陪诊小程序关爱健康,无忧陪伴
随着社会发展和人们生活水平的提高,健康问题成为人们关注的焦点。然而,在就医过程中,许多患者常常感到孤独和无助,缺乏得到家人陪伴的温暖与安慰。为了解决这一问题,我们公司开发了一款创新的陪诊小程序软件࿰…...
uni-app小程序使用DCloud(插件市场)流程
一、DCloud(插件市场) DCloud 是uni-app官方插件市场,里面有官方、团队、个人发布的众多插件,包括uni-ui、uni-pay 等。而像uni-ui这种大型组件库都有官方文档可参考,但一些团队或个人发布的小型插件没有文档…...
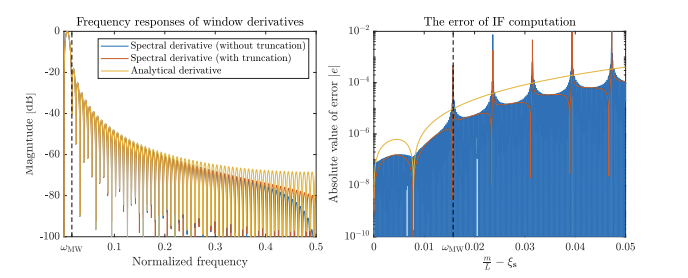
非平稳信号分析和处理、STFT的瞬时频率研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

SIPp使用经验
xml文件,建议<?xml version"1.0" encoding"UTF-8" ?>,不建议ISO-8859-1命令行传key参数 sipp -key contact_port 9999 ...<send retrans"500"><![CDATA[REGISTER sip:[field1]:[remote_port] SIP/2.0Vi…...
ChessGPT:免费好用的国际象棋对弈AI机器人
对于国际象棋初学者,需要找一个对手来练棋。ChessGPT,就是一个免费好用的AI对弈机器人,非常适合新手来提升,是一个很好的练习伙伴。网站地址是:https://www.chess.com/play/computer,也有手机版app…...
【java】A卷+B卷)
华为OD 区间交集(200分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...
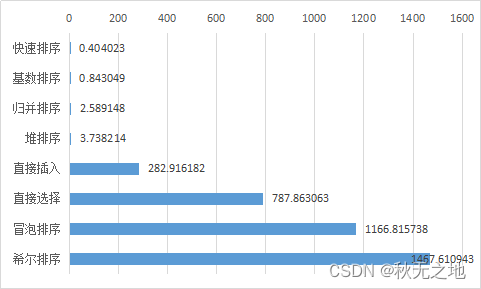
Python算法:八大排序算法以及速度比较
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

半导体用超高纯管材行业头部企业市场占有率及排名调研报告
内容摘要 本文调研和分析全球半导体用超高纯管材发展现状及未来趋势,核心内容如下: (1)全球市场总体规模,分别按销量和按收入进行了统计分析,历史数据2018-2022年,预测数据2023至2029年。 &…...

Qt中的线程同步:确保多线程程序的安全性
在现代计算机编程中,多线程编程已经变得非常常见,因为它可以提高程序的性能和响应能力。然而,多线程编程也引入了许多挑战,其中一个主要挑战是线程同步。线程同步是确保多个线程协同工作时数据的安全性和一致性的关键问题。Qt作为一种流行的C++框架,提供了丰富的工具和类来…...
ESRI ArcGIS Desktop 10.8.2图文安装教程及下载
ArcGIS 是由美国著名的地理信息系统公司 Esri 开发的一款地理信息系统软件,它是目前全球最流行的 GIS 软件之一。ArcGIS 提供了图形化用户界面和数据分析工具,可以帮助用户管理、分析和可视化各种空间数据。ArcGIS Desktop是一个完整的桌面GIS软件套件&a…...
笔记本电脑Windows10安装
0 前提 安装windows10的电脑为老版联想笔记本电脑,内部没有硬盘,临时加装了1T的硬盘。 1u盘准备 准备u盘,大小大于16G。u盘作为系统盘时,需要将内部的其他文件备份,然后格式化。u盘格式化后,插入一款可以…...
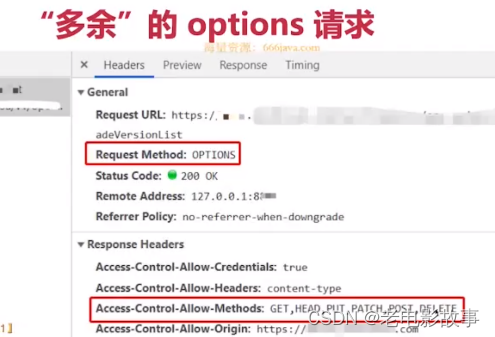
跨域方案的抉择
前言 遇到跨域问题的时候,到底是使用CORS来解决,还是使用代理呢? 判断依据不是技术层面,而是你的生产环境。 首先要关注的是生产环境里面到底是一种什么样的情况,到底有没有跨域,然后根据生产环境的情况&a…...
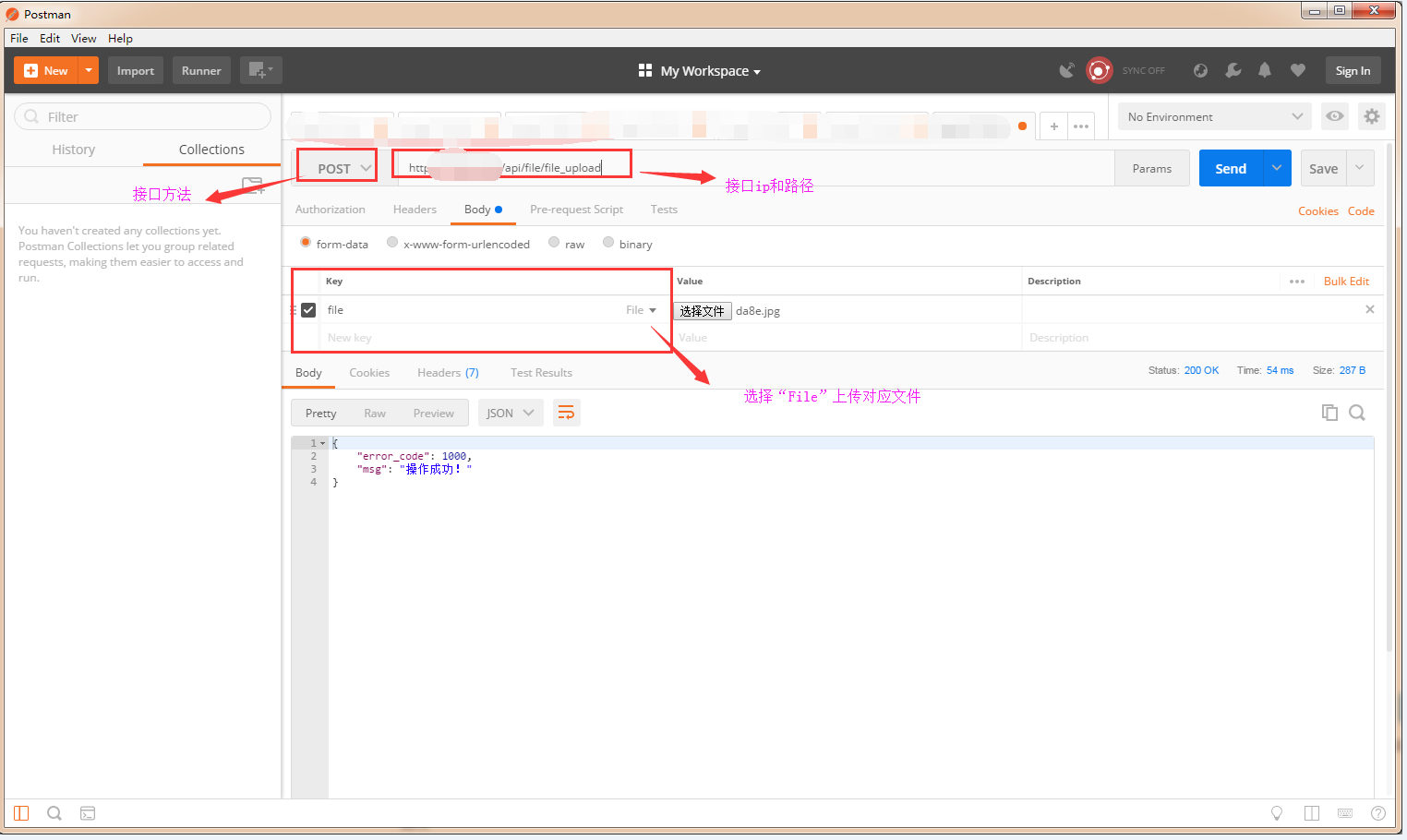
接口测试(jmeter和postman 接口使用)
接口测试基础知识 接口测试主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点。把前端(client)和后端(server)联系起来,测试的重点是要检查数据的交换,传递和控制管理过程,以及系…...
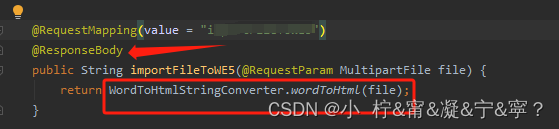
doc与docx文档转html,格式样式不变(包含图片转换)
最近做一个富文本的需求,要求把文档内容转换到富文本内,文档中的格式也好,样式也好,图片啥的都要一致展示;踩了不少坑,据说word文档其实是一个压缩包,我不是特别清楚但是也能理解,自…...
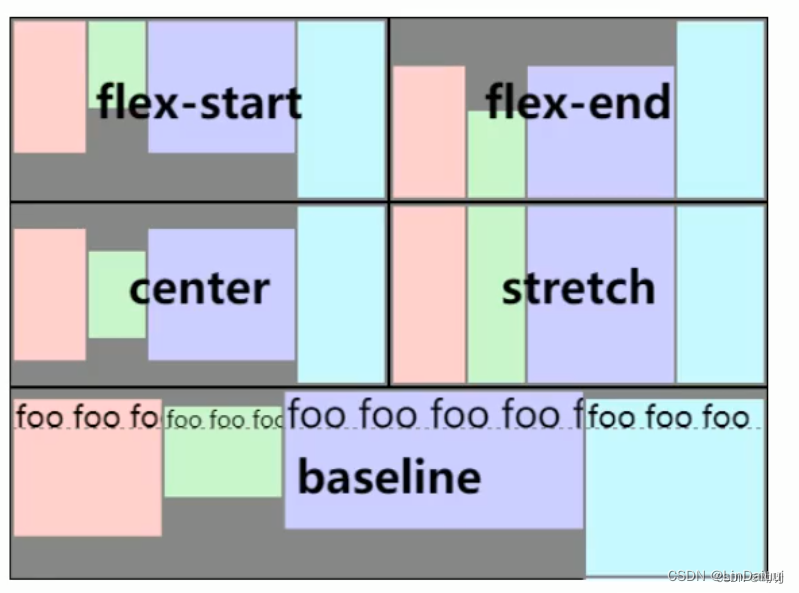
CSS页面基本布局
前提回顾 1. 超文本标记语言(HTML)是一种标记语言,用来结构化我们的网页内容并赋予内容含义; (超文本标记语言(英语:HyperText Markup Language /ˈhaɪpətekst ˈmɑːkʌp ˈlŋɡwɪdʒ /…...
SQL查询命令互转vba格式
最近搞个Excel的vba查询数据库,发现vba有代码行长度限制需要转换下就弄了这个,布局和功能暂且这样了,哪位大佬如果有兴趣的可以再美化下! 这次更新了SQL命令互转VBA格式, SQL原始格式要分行的不能一坨贴进去࿰…...

android 指针动画转动
记录一种简单动画 效果图: 都是直接使用图片资源FrameLayout布局实现,布局如下: <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-auto"…...
力扣第51题 N 皇后 c++ 难~ 回溯题
题目 51. N 皇后 困难 相关标签 数组 回溯 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ࿰…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
