力扣第51题 N 皇后 c++ 难~ 回溯题
题目
51. N 皇后
困难
相关标签
数组 回溯
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
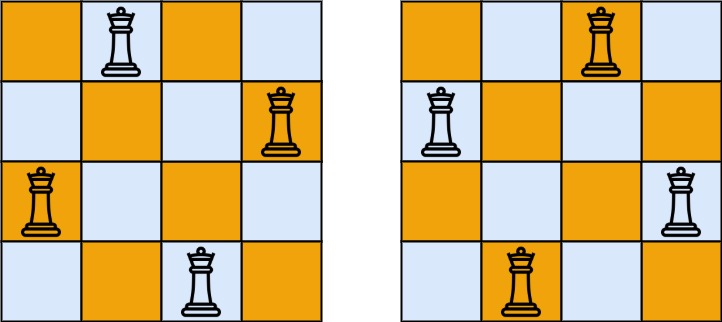
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:[["Q"]]
提示:
1 <= n <= 9
思路和解题方法
首先,定义了一个名为 Solution 的类。其中:
- ans:成员变量,用于记录所有可行的 N 皇后方案;
- backtracking:回溯函数,用来尝试放置 N 个皇后;
- isvalid:函数,用于检查当前位置是否可放置皇后;
- solveNQueens:主函数,使用回溯法求解 N 皇后问题。
在 backtracking 函数中:
- 当已经成功放置 N 个皇后时,将当前的棋盘加入答案数组 ans 中。
- 对于每一行,在第 col 列尝试放置皇后,如果该格子可行,则标记上皇后,继续向下一行进行搜索,搜索完后回溯到上一步位置并取消标记;
- 搜索过程中,调用函数 isvalid 进行当前位置是否可放的判断。
在 isvalid 函数中:
- 检查当前列是否已经有皇后;
- 检查左上方是否已经有皇后;
- 检查右上方是否已经有皇后;
- 如果以上均未出现皇后,则说明该位置可放置皇后,返回真。
而在主函数 solveNQueens 中:
- 清空答案数组 ans,并定义初始棋盘状态 chessboard;
- 调用回溯函数 backtracking 在 chessboard 中查找所有可行的 N 皇后方案;
- 返回答案数组 ans。
复杂度
时间复杂度:
O(n!)
算法的时间复杂度为 O(n!),其中 n 表示棋盘大小。因为每一行只能放置一个皇后,所以在搜索下一行的时候,需要排除已经放置的皇后所在的列和两条对角线上的位置,因此每一行可选的位置数是 n,总的搜索次数是 n×(n−2)×(n−4)×⋯1=n!。
空间复杂度
O(n^2)
算法的空间复杂度是 O(n2),因为需要使用一个 n×n 的二维数组
chessboard来存储棋盘状态,同时还需要使用一个二维数组ans来存储所有可行的 N 皇后方案。
c++ 代码
class Solution {
public:vector<vector<string>> ans; // 存储所有可行的 N 皇后方案void backtracking(int n, int row, vector<string> &chessboard){if (row == n) // 若已成功放置 N 个皇后,将当前棋盘加入答案数组{ans.push_back(chessboard);return;}for (int col = 0; col < n; col++) // 在当前行的每一列尝试放置皇后{if (isvalid(row, col, chessboard, n)) // 若当前位置可放置皇后{chessboard[row][col] = 'Q'; // 放置皇后backtracking(n, row + 1, chessboard); // 继续下一行的搜索chessboard[row][col] = '.'; // 回溯到上一步,取消该位置的皇后标记}}}bool isvalid(int row, int col, vector<string> &chessboard, int n){for (int i = 0; i < row; i++){if (chessboard[i][col] == 'Q') // 检查当前列是否已经有皇后return false;}for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--){if (chessboard[i][j] == 'Q') // 检查左上方是否已经有皇后return false;}for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++){if (chessboard[i][j] == 'Q') // 检查右上方是否已经有皇后return false;}return true; // 当前位置可放置皇后}vector<vector<string>> solveNQueens(int n) {ans.clear(); // 清空答案数组vector<string> chessboard(n, string(n, '.')); // 初始化棋盘backtracking(n, 0, chessboard); // 调用回溯函数开始搜索return ans; // 返回所有可行的 N 皇后方案}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第51题 N 皇后 c++ 难~ 回溯题
题目 51. N 皇后 困难 相关标签 数组 回溯 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ࿰…...

【摄影】基础笔记
摄影基础 合理选择器材1.定焦镜(画质更好,有利于联系构图)2.变焦镜(拍摄便捷灵活,有利于快速捕捉)3.了解焦距 合理利用景深1.焦段2.光圈3.背景距离 焦距与参数实用相机参数设置指南高效的快速对焦法&#x…...

【广州华锐互动】VR石油钻井井控实训系统
在过去的几十年中,石油工业的发展速度一直在加快。为了适应这个快速发展的行业,需要新的技术和工具,而VR(虚拟现实)技术正是其中之一。本文将探讨VR石油钻井井控实训系统在石油工业教育中的应用。 在真实的钻井环境中&…...
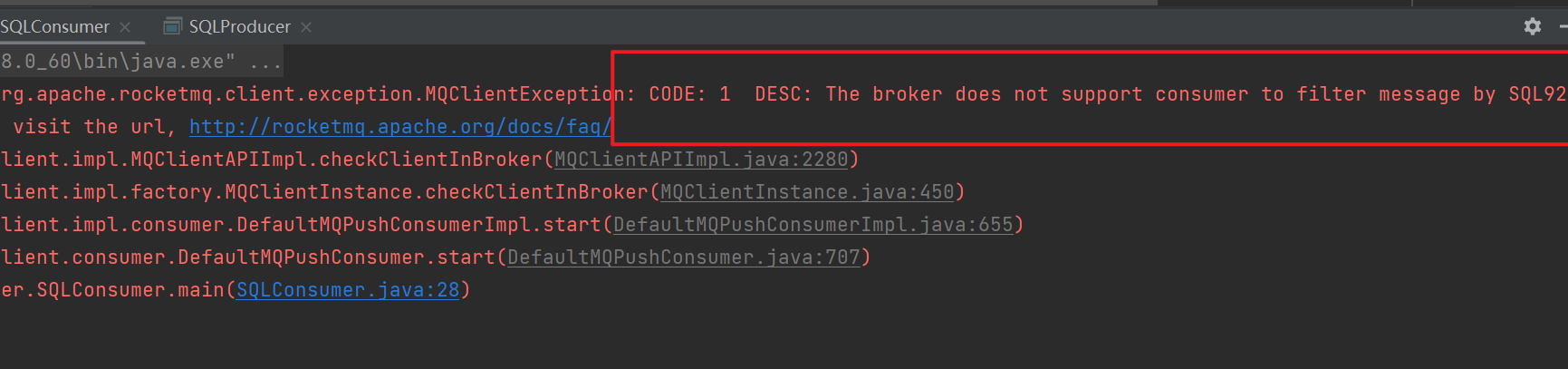
【RocketMQ系列五】消息示例-顺序消息延迟消息广播消息的实现
1. 前言 上一篇文章我们介绍了简单消息的实现,本文将主要来介绍顺序消息的实现,顺序消息分为局部顺序消息和全局顺序消息。 顺序消息指的是消费者在消费消息时,按照生产者发送消息的顺序进行消费。即先发送的先消费【FIFO】。 顺序消息分为…...

hdfs dfsadmin -safemode无法退出安全模式
退出安全模式 第一种:正常退出安全模式 hdfs dfsadmin -safemode leave如提示Safe mode is OFF,那就说明退出成功,但有时候这个命令也没办法退出安全模式,就需要使用强制退出 第二种:强制退出安全模式 hdfs dfsadmin …...

git 新建 branch 推送 到服务器
通常情况下,需要开发一个模块,从 master 新建立了一个 分支,newbranch,如果推送到服务器; 1:从远程 master 建立本地分支 newbranch; git checkout -b newbranch origin/master 2:当修改完成代码…...

安全渗透测试基础知识之网络基础知识
一、OSI七层模型 7应用层6表示层5会话层4传输层3网络层2数据链路层1物理层1.物理层 提供通信介质和接口标准 网线 2.网络链路层 提供二层寻扯/MAC地址和二层通信(交换机)功能 协议:以太网Ethernet 3.网络层 提供三层寻扯/IP地址和三层通信(路由器...
和加载指定资源)
Unity Editor 打包指定资源(AssetBundle)和加载指定资源
前言: 一般用于ui资源打包和加载,代码比较简单没什么好说的,直接上代码。 打包代码: [MenuItem("Assets/打包指定的预设")]public static void BuildAsset() {var selectObject Selection.activeObject;if (selectObje…...

网站批量替换关键词方法
注意替换操作之前先对文件做好备份 1.下载http://downinfo.myhostadmin.net/ultrareplace5.02.rar 解压出来,运行UltraReplace.exe 2.点击菜单栏中的配置,全选所有文件类型,或者根据自己的需求选择部分,如htm、html、php、asp等 3.若替换单个文件,点击文件,若是要…...
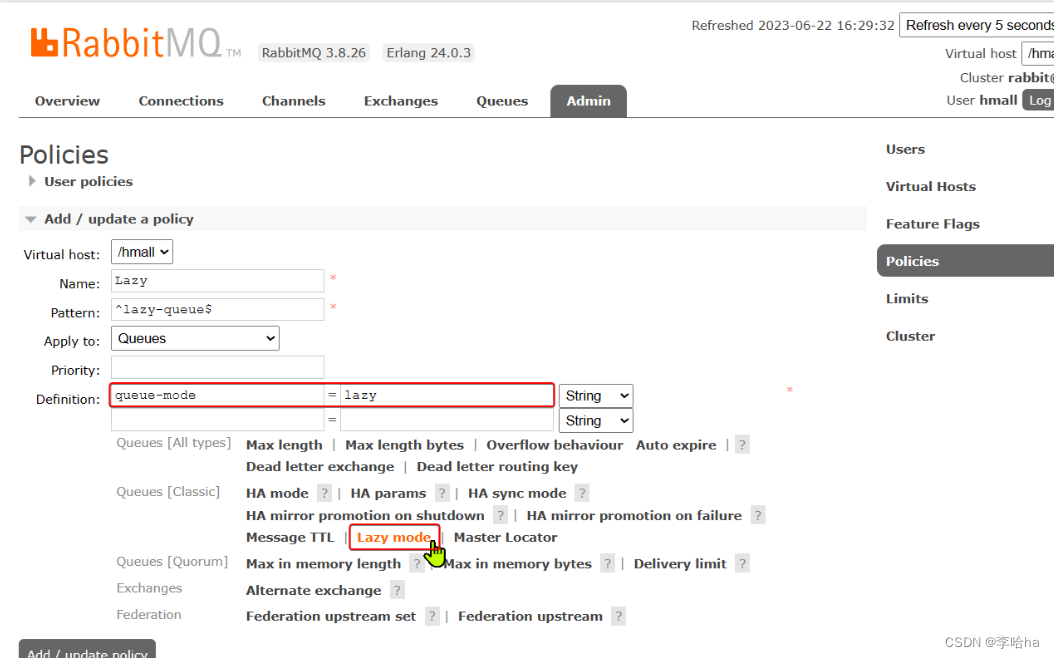
RabbitMQ的LazyQueue
在默认情况下,RabbitMQ会将接收到的信息保存在内存中以降低消息收发的延迟。但在某些特殊情况下,这会导致消息积压,比如: 消费者宕机或出现网络故障消息发送量激增,超过了消费者处理速度消费者处理业务发生阻塞 一旦…...

面试经典150题——Day16
文章目录 一、题目二、题解 一、题目 42. Trapping Rain Water Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining. Example 1: Input: height [0,1,0,2,1,0,1,3,2,1,2,…...

从零开始搭建第一个django项目
目录 配置环境创建 Django 项目和 APP项目组成 子目录文件组成应用文件组成 配置 settings.py启动项目 数据表创建models.pyDjango-models的常用字段和常用配置 Django-admin 引入admin后台和管理员外键views.pyurls.pypostman接口测试 QuerySetInstance功能APIView 的概念…...

Godot2D角色导航-自动寻路教程(Godot获取导航路径)
文章目录 开始准备获取路径全局点坐标 开始准备 首先创建一个导航场景,具体内容参考下列文章: Godot实现角色随鼠标移动 然后我们需要设置它的导航目标位置,具体关于位置的讲解在下面这个文章: Godot设置导航代理的目标位置 获取…...

用c++写一个高精度计算的减法运算
这段代码是一个用C编写的程序,它实现了两个大整数的减法运算。 #include<iostream> #include<cstdio> #include<cstring> using namespace std;int main(){int a[256],b[256],c[256],lena,lenb,lenc,i;char n[256],n1[256]"1001",n2[2…...

基于白鲸优化的BP神经网络(分类应用) - 附代码
基于白鲸优化的BP神经网络(分类应用) - 附代码 文章目录 基于白鲸优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.白鲸优化BP神经网络3.1 BP神经网络参数设置3.2 白鲸算法应用 4.测试结果:5.M…...
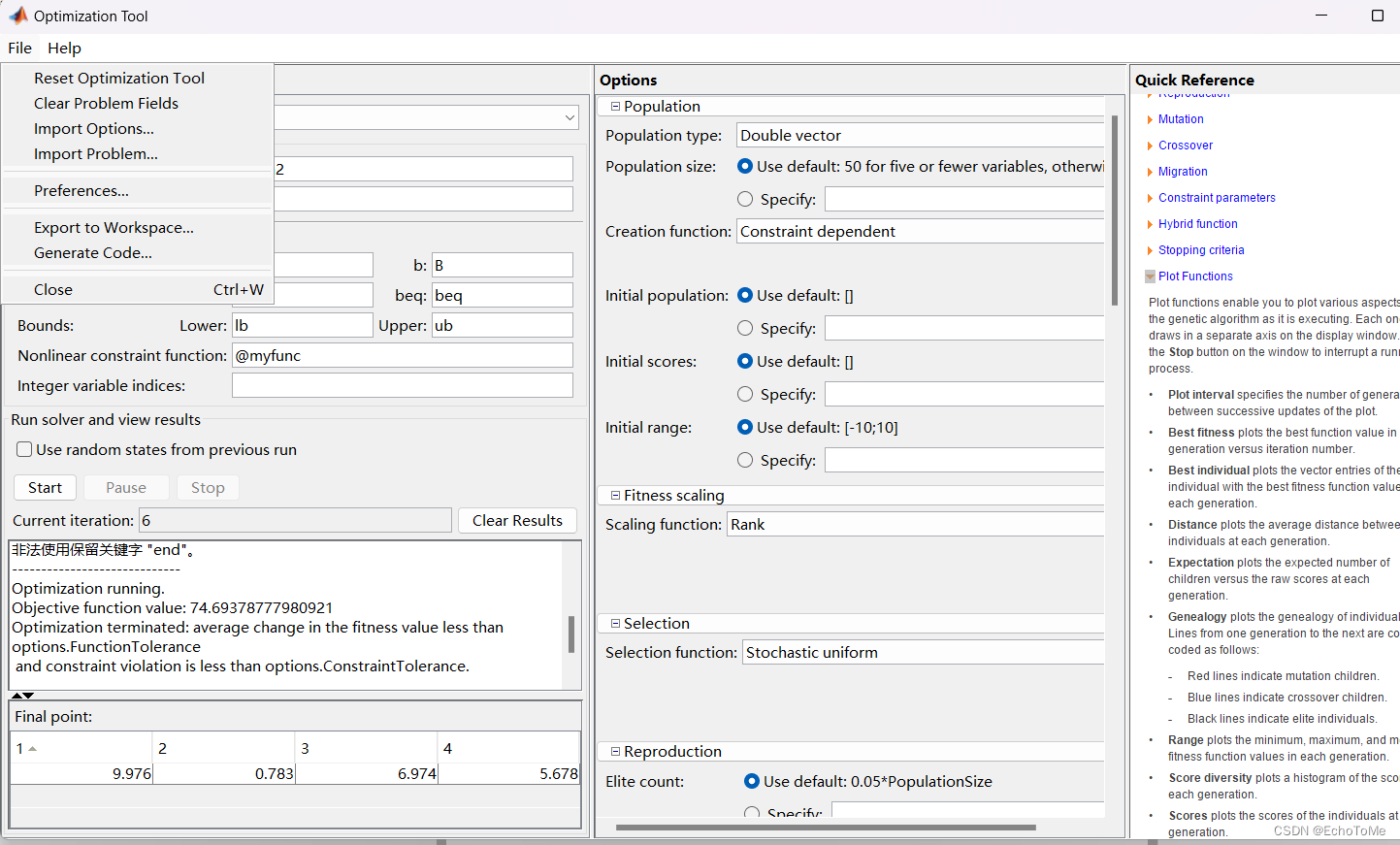
Matlab遗传算法工具箱——一个例子搞懂遗传算法
解决问题 我们一般使用遗传算法是用来处理最优解问题的,下面是一个最优解问题的例子 打开遗传算法工具箱 ①在Matlab界面找到应用程序选项,点击应用程序(英文版的Matlab可以点击App选项) ②找到Optimization工具箱,点击打开 创建所需要…...
Coreldraw2020最新64位电脑完整版本下载教程
安装之前所有的杀毒软件都要退出。无论是360,腾讯管家,或者电脑自带的安全中心,要不然会阻止安装。 CorelDRAW2020版win下载如下:https://wm.makeding.com/iclk/?zoneid55678 CorelDRAW2020版mac下载如下:https://wm.makeding.com/iclk/?…...
第一节——vue安装+前端工程化
作者:尤雨溪 官网:简介 | Vue.js 脚手架文档 创建一个项目 | Vue CLI 一、概念(了解) 是一套用于构建用户界面的渐进式框架。与其它大型框架不同的是,Vue 被设计为可以自底向上逐层应用。Vue 的核心库只关注视图层&…...
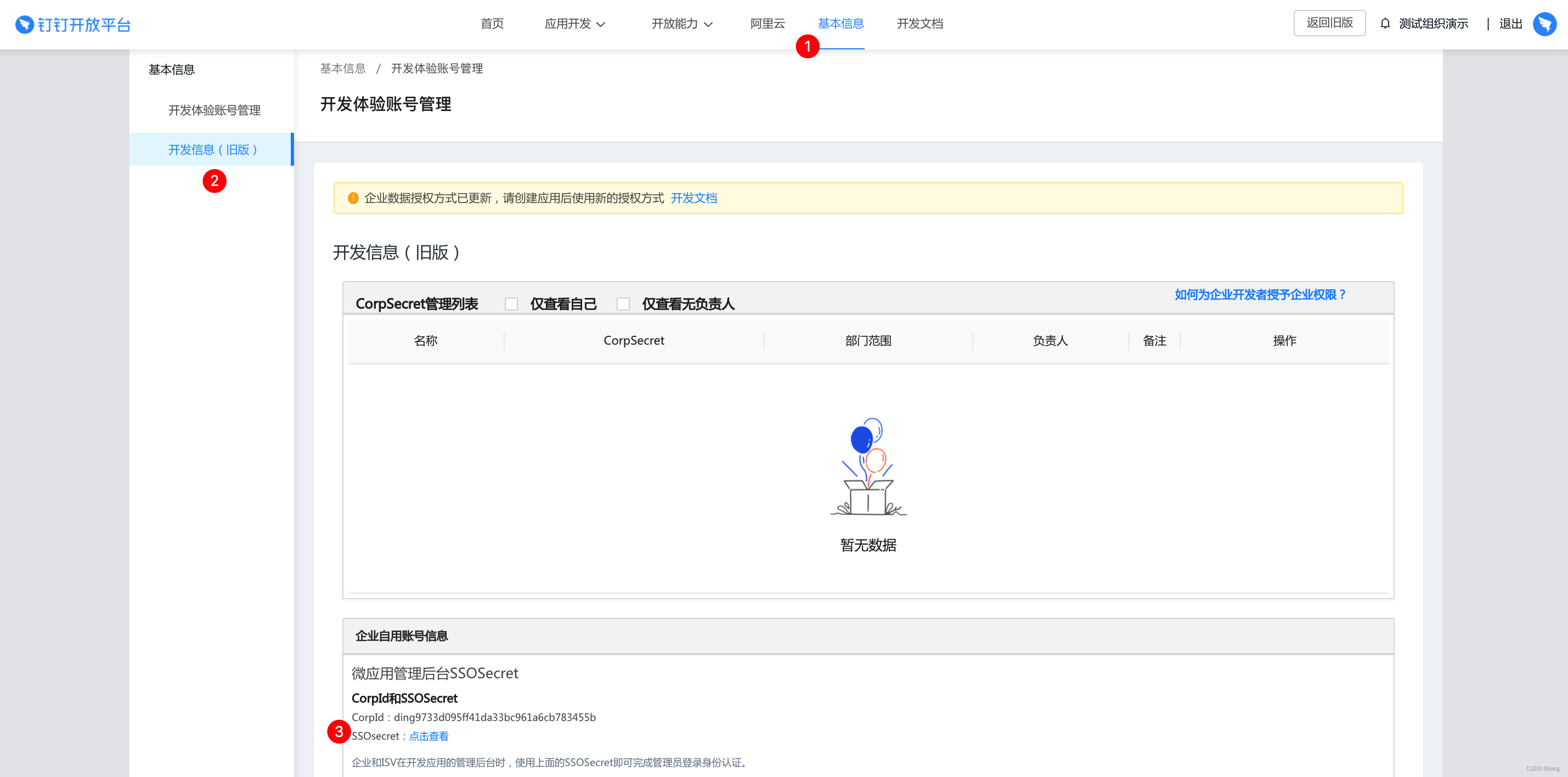
vue集成钉钉单点登录
初始环境判断 判断是否是来自钉钉环境的访问,返回:boolean类型值 window.navigator.userAgent.includes("DingTalk")前端引入vue中钉钉相关的依赖,并获取钉钉的临时授权码 import * as dingtalk from dingtalk-jsapi; let that …...
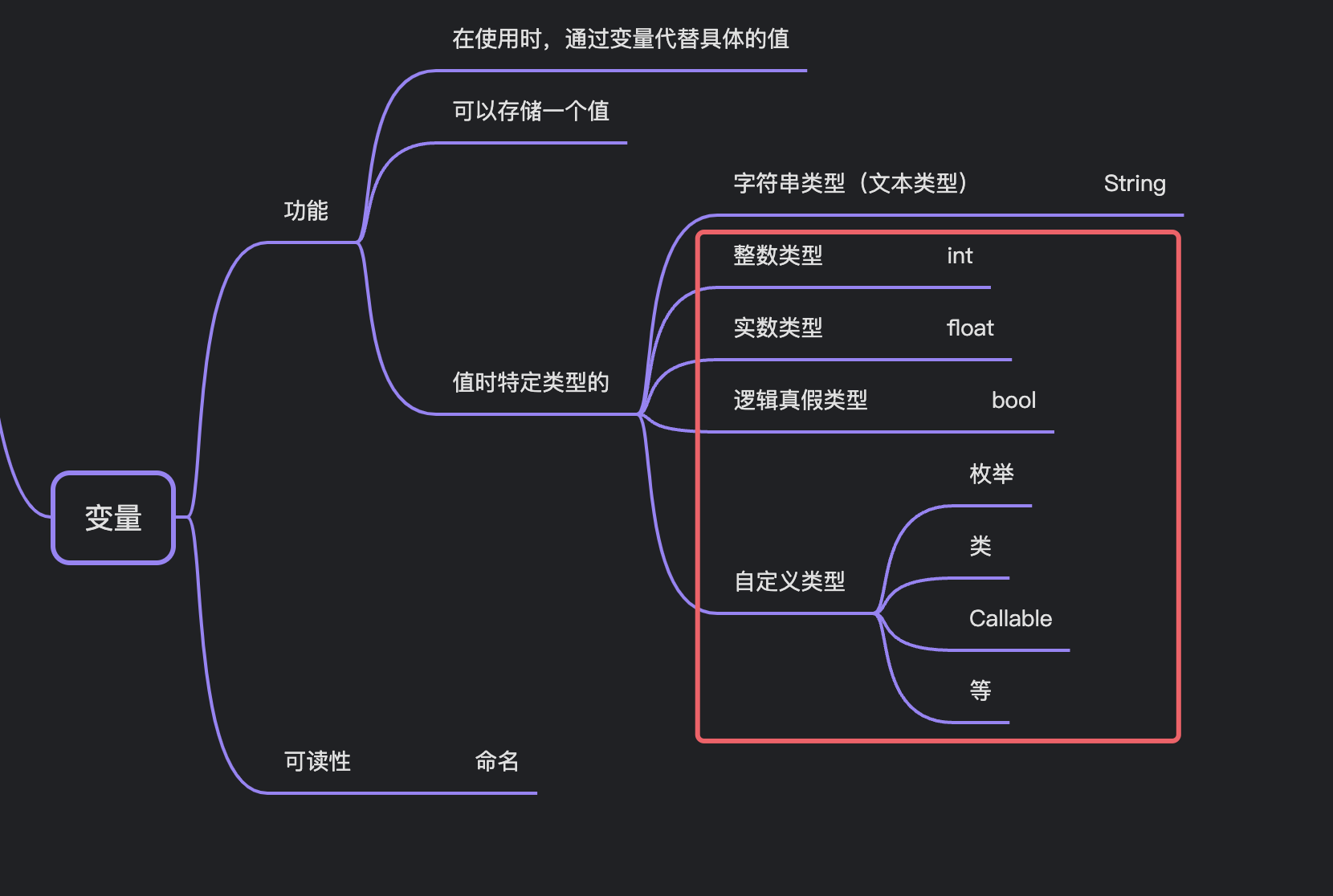
凉鞋的 Godot 笔记 203. 变量的常用类型
203. 变量的常用类型 在上一篇,我们对变量进行了概述和简介,知识地图如下: 我们已经接触了,变量的字符串类型,以及一些功能。 在这一篇,我们尝试多接触一些变量的类型。 首先是整数类型。 整数类型 整…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
