黎曼几何与切空间之间的投影
公式:
从黎曼空间投影到切空间,其中P为黎曼均值,也是切空间的参考中心点,Pi是要投影到切空间的点。
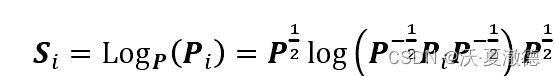
从切空间投影回来,其中Si为切空间中的向量。
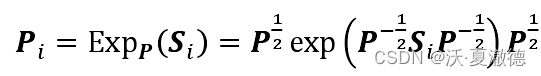
function Tcov = CovToTan(cov,Mcov)Cm12 = Mcov^(-1/2);X_new = logm(Cm12 * cov * Cm12);C12 = Mcov^(1/2);Tcov = Mupper(C12 * X_new * C12);
endfunction Cov = TanToCov(vec,Mcov)X = Munupper(vec);Cm12 = Mcov^(-1/2);X = Cm12 * X * Cm12;C12 = Mcov^(1/2);Cov = C12 * expm(X) * C12;
endfunction T = Mupper(X)% Upper triangular part vectorization with diagonal preservation.% This function keeps the upper triangular part of the matrix and% vectorizes it while multiplying non-diagonal elements by sqrt(2).% Get the size of X[M, N] = size(X);% Check if matrices are squareif M ~= Nerror('Matrices must be square');end% Initialize T with zerosT = zeros(M, M, 'like', X);% Calculate the multiplier for non-diagonal elementsmultiplier = sqrt(2);% Fill T with the upper triangular part, preserving the diagonalfor i = 1:Mfor j = i:Mif i == jT(i, j) = X(i, j); % Diagonal element remains the sameelseT(i, j) = X(i, j) * multiplier; % Non-diagonal elements multiplied by sqrt(2)endendend% Flatten the upper triangular part of T to a vectorT = T(triu(true(size(T))) == 1);T = T';
endfunction X = Munupper(T, n)% Reverse the operation to reconstruct the matrix from its upper triangular part.% Calculate the size of the square matrix based on the length of the input vector Tn = round((sqrt(1 + 8 * length(T)) - 1) / 2);% Check if T is a valid upper triangular vectorm = n * (n + 1) / 2;if numel(T) ~= merror('Invalid input. Input vector size does not match the expected size for upper triangular vectors.');end% Initialize the symmetric matrix X with zerosX = zeros(n, n, 'like', T);% Calculate the indices for the upper triangular part[I, J] = find(triu(ones(n)));% Reverse the vectorization and apply the appropriate scaling to non-diagonal elementsfor k = 1:numel(I)i = I(k);j = J(k);if i == jX(i, j) = T(k); % Diagonal elements remain the sameelseX(i, j) = T(k) / sqrt(2); % Reverse scaling for non-diagonal elementsX(j, i) = X(i, j); % Symmetric matrixendend
end相关文章:
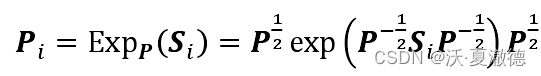
黎曼几何与切空间之间的投影
公式: 从黎曼空间投影到切空间,其中P为黎曼均值,也是切空间的参考中心点,Pi是要投影到切空间的点。 从切空间投影回来,其中Si为切空间中的向量。 function Tcov CovToTan(cov,Mcov)Cm12 Mcov^(-1/2);X_new logm(Cm…...
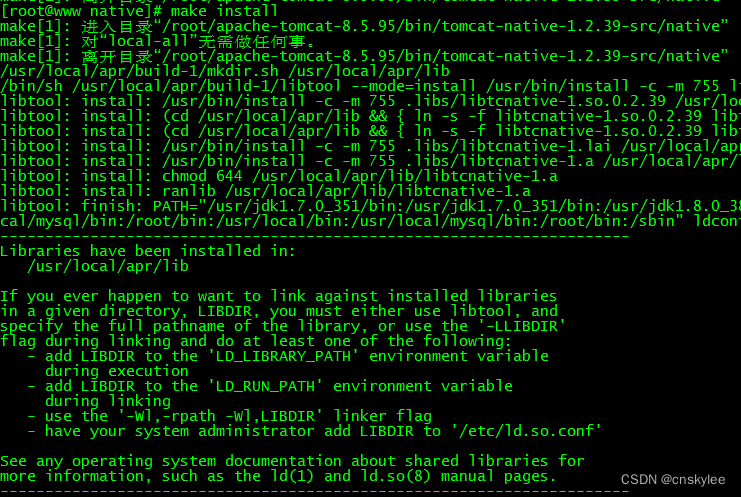
【Tomcat】为Tomcat服务配置本地Apr库以提升性能
关于 apr 和 apr-util 对 Tomcat 服务的性能提升的说明: 要测APR给tomcat带来的好处最好的方法是在慢速网络上(模拟Internet),将Tomcat线程数开到300以上的水平,然后模拟一大堆并发请求。如果不配APR,基本…...

普通人在当前大环境下——少看宏观,多看具体
前言 宏观叙事,简而言之,就是从宏观把握历史社会的发展,寻找其中永恒的共性。我们大概听过此类的话:贸易战导致本地经济下滑、气候变化是因为过去几十年的工业发展、大环境不行导致不赚钱。此类叙事方式,身边人聊的甚欢,在媒体、社交圈、日常社群交流中,随处可见。以前…...

用echarts在vue2中实现3d饼图
先看效果,再看文章: 一、安装插件 3d的图不仅用到echarts,还用到了echarts-gl,因此都需要安装一下哦~ npm install echarts npm install echarts-gl2.0.9 //可以指定版本,也可不指定二、在main.js中引入 import * …...
低代码助力软件开发
低代码开发工具正在日益变得强大,它正不断弥合着前后端开发之间的差距。对于后端来说,基于低代码平台开发应用时,完全不用担心前端的打包、部署等问题,也不用学习各种框架(Vue、React、Angular等等)&#x…...

C嘎嘎之类和对象上
> 作者简介:დ旧言~,目前大二,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:掌握类的引用和定义,熟悉类成员函数的…...
Vue 3使用 Iconify 作为图标库与图标离线加载的方法、 Icones 开源在线图标浏览库的使用
之前一直naive-ui搭配使用的是xicons,后来发现Iconify支持的图标合集更多,因此转而使用Iconify。 与FontAwesome不同的是,Iconify配合Icones相当于是一个合集,Iconify提供了快捷引入图标的方式,而Icones是一个大的图标…...
springboot+vue基于Spark的共享单车数据存储系统的设计与实现【内含源码+文档+部署教程】
博主介绍:✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立工作室。专注于计算机相关专业毕业设计项目实战6年之久,选择我们就是选择放心、选择安心毕业✌ 🍅由于篇幅限制,想要获取完整文章或者源码,或者代做&am…...

如何使双核心的ESP32开启双核功能同时执行多任务
如何使双核心的ESP32开启双核功能同时执行多任务 简介查看ESP32当前哪一个内核在执行任务双核同时执行任务总结 简介 ESP32-WROOM-32模组内置两个低功耗 Xtensa 32-bit LX6 MCU,两个 CPU 核(core 0与core 1)可以被单独控制。可以在两个内核上…...
Node.js在Python中的应用实例解析
随着互联网的发展,数据爬取成为了获取信息的重要手段。本文将以豆瓣网为案例,通过技术问答的方式,介绍如何使用Node.js在Python中实现数据爬取,并提供详细的实现代码过程。 Node.js是一个基于Chrome V8引擎的JavaScript运行时环境…...
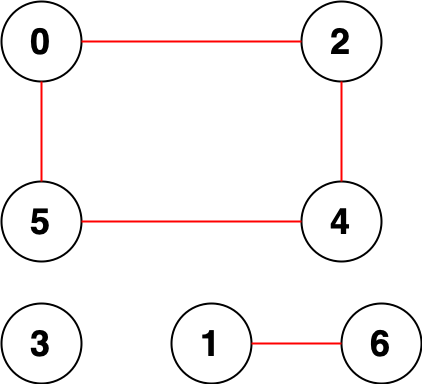
LC-2316. 统计无向图中无法互相到达点对数(DFS、并查集)
2316. 统计无向图中无法互相到达点对数 中等 给你一个整数 n ,表示一张 无向图 中有 n 个节点,编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。 请你返回 无法互相…...

git笔记 - 常用记录
第1阶段 - Git简介 什么是Git及其重要性?基本的Git概念和术语 仓库(Repository):也称为 repo,是存储代码和版本历史的地方。它可以是本地仓库(在本地计算机上)或远程仓库(在服务器…...
无纸化办公小程序数据交互、wxs的使用
前言 很多同志们再写小程序的过程中,不知道该怎么发起HTTP请求到后端,在Web环境中发起HTTPS请求是很常见的,但是微信小程序是腾讯内部的产品,不能直接打开一个外部的链接。例如,在微信小程序中不能直接打开www.taobao…...
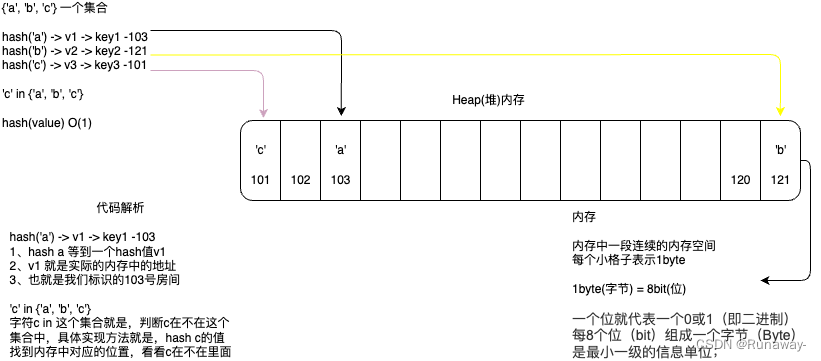
Python之哈希表-哈希表原理
Python之哈希表-哈希表原理 集合Set 集合,简称集。由任意个元素构成的集体。高级语言都实现了这个非常重要的数据结构类型。Python中,它是可变的、无序的、不重复的元素的集合 初始化 set() -> new empty set objectset(iterable) -> new set …...
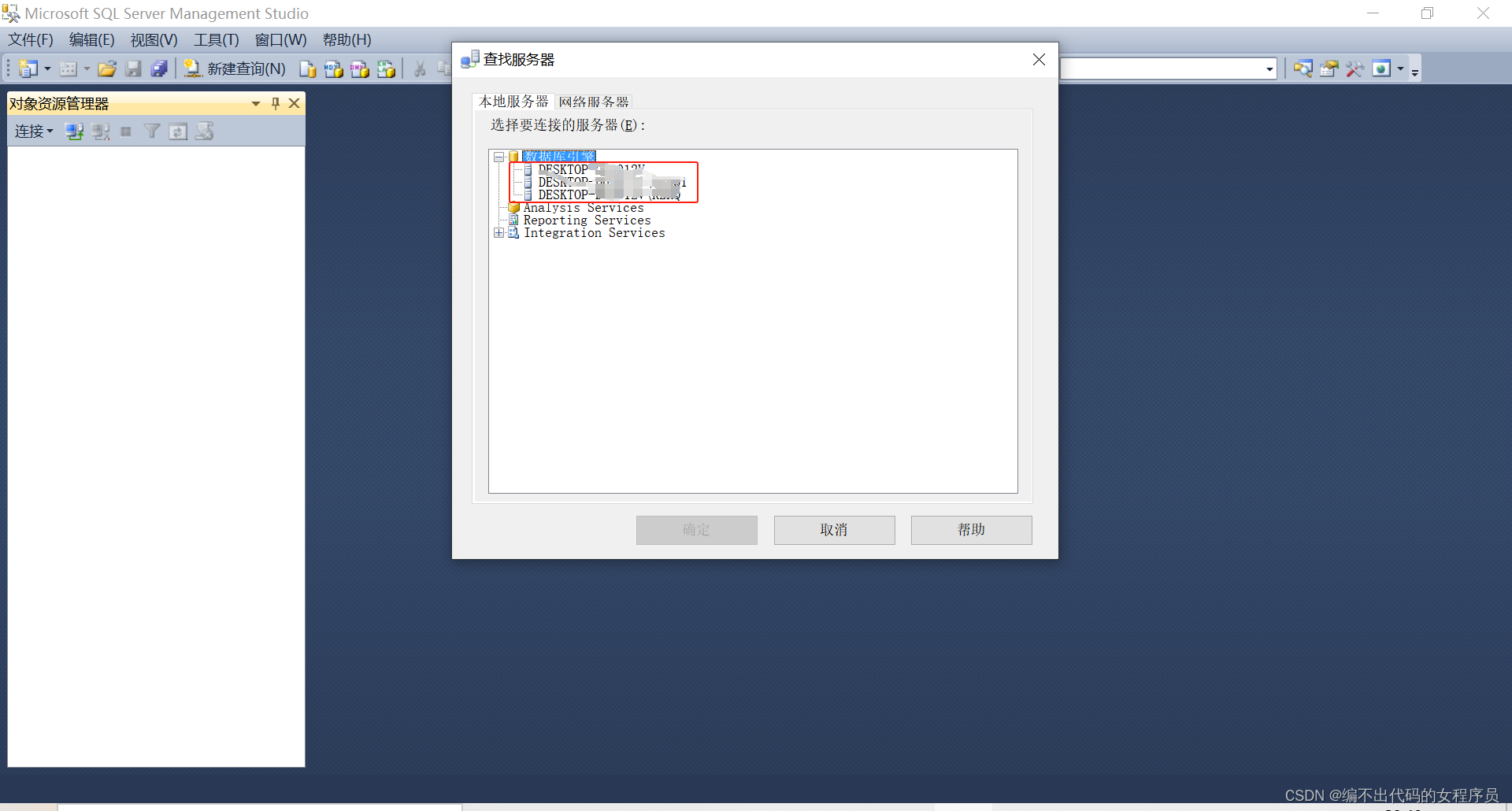
sql server2014如何添加多个实例 | 以及如何删除多个实例中的单个实例
标题sql server2014如何添加多个实例 前提(已安装sql server2014 且已有默认实例MSSQLSERVER) 添加新的实例 其实就是根据安装步骤再安装一次(区别在过程中说明) 双击安装 选择“全新独立安装或添加现有功能” 然后下一步下一…...

C++ 智能指针常用总结
C 智能指针常用总结 文章目录 C 智能指针常用总结1. 写在对前面2. why 智能指针3. what 智能指针3.1 unique_ptr3.2 shared_ptr3.3 weak_ptr 3. how 指针指针3.1 unique_ptr3.1.1 创建3.1.2 成员函数 3.2 shared_ptr3.2.1创建3.2.2 成员对象 3.3 weak_ptr 4. 碎碎念5.参考资料 …...

OracleRAC 安装配置过程中的问题
OS RHAS 3.2 DB 9204 在RAC的安装配置过程中,虽然是严格仔细按照文档来实施,但还是出现不少问题,现整理出来。 现象一 : 在节点一安装数据库的时候出现以下错误 [oraclerac1 dbs]$ sqlplus "/nolog"SQL*Plus: Relea…...

基于战争策略优化的BP神经网络(分类应用) - 附代码
基于战争策略优化的BP神经网络(分类应用) - 附代码 文章目录 基于战争策略优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.战争策略优化BP神经网络3.1 BP神经网络参数设置3.2 战争策略算法应用 4.测试结果…...
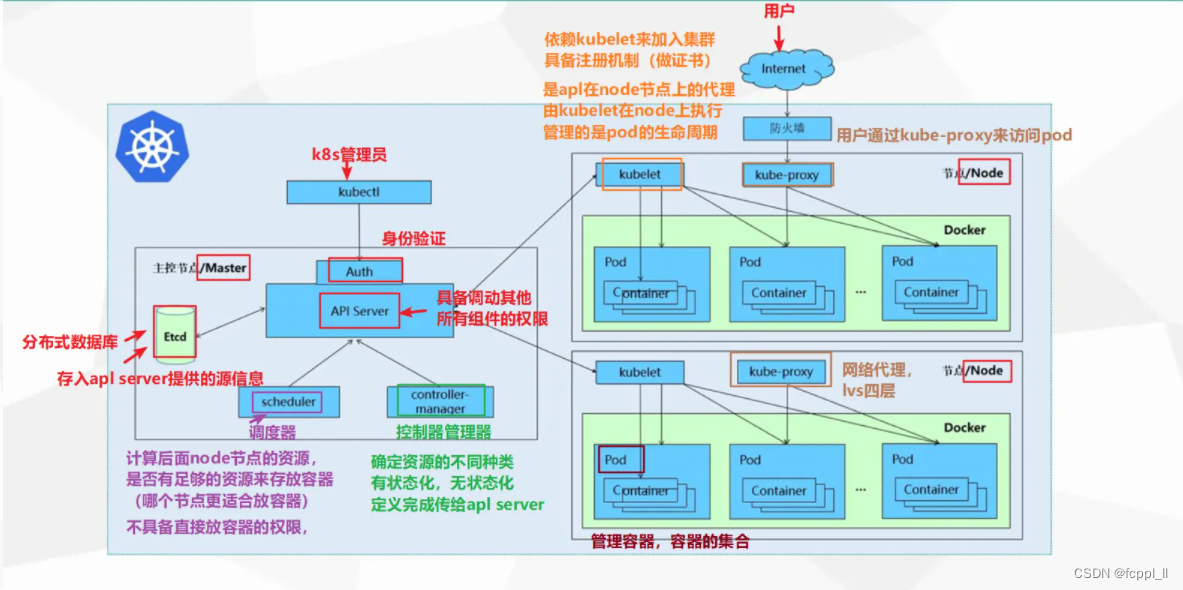
K8s 概念及组件
K8s 的全称为Kubernetes,是一种开源的容器编排平台,用于自动化部署以及扩展和管理容器化的应用程序,它提供了一种容器编排和管理的方式,可以帮助开发人员更轻松的管理容器化的应用程序,并且提供了一种跨多个主机的自动…...

【已解决】java的gradle项目报错org.gradle .api.plugins .MavenPlugin
我的java的gradle项目经常报错org.gradle .api.plugins .MavenPlugin。报错这个问题是因为依赖起冲突了,我在网上试了很多方法都没有效果,折让小编我很是苦恼,不过还好到最后问题还是解决了。 首先要知道你的项目所使用的gradle版本…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
