量子信息处理器可能能够提供高度压缩的生成对抗学习任务的版本
量子信息处理在生成对抗学习任务中的应用可能性,以及量子信息处理器在表示高维向量和执行线性代数运算上的优势。
举个例子
假设底层数据由M个在N维实数或复数空间中的归一化向量~vj组成,使得数据的(归一化)协方差矩阵为C = (1/M) ∑j vjv†j。一个量子信息处理器可以通过logN个量子比特来表示这些向量的量子态|vji,并且数据的归一化协方差矩阵等于密度矩阵ρ = (1/M) ∑j |vjihvj|。
让我们举一个具体的数值例子来说明。假设我们有M=3个归一化向量~v1, ~v2, ~v3,每个向量都是N=2维的实数向量。那么数据的协方差矩阵C为:
C = (1/3) (v1v†1 + v2v†2 + v3v†3)
假设向量~v1 = [1, 0],~v2 = [0, 1],~v3 = [1, 1],那么协方差矩阵C可以计算为:
C = (1/3) ([1, 0] [1, 0]† + [0, 1] [0, 1]† + [1, 1] [1, 1]†)
= (1/3) ([1, 0] [1, 0] + [0, 1] [0, 1] + [1, 1] [1, 1])
= (1/3) ([1, 0] + [0, 1] + [2, 2])
= (1/3) [3, 3]
= [1, 1]
因此,对于这个具体的数值例子,数据的归一化协方差矩阵C为[1, 1]。
接下来,我们可以用量子态来表示这些向量。每个向量可以用logN=1个量子比特来表示。所以,我们有三个量子态|v11>, |v21>和|v31>来表示~v1, v2和v3。那么数据的密度矩阵ρ为:
ρ = (1/3) (|v11><v11| + |v21><v21| + |v31><v31|)
假设|v11> = |0>,|v21> = |1>,|v31> = (1/√2)(|0> + |1>),那么密度矩阵ρ可以计算为:
ρ = (1/3) (|0><0| + (3/2)|0><1| + (3/2)|1><0| + |1><1|)
---------------------------
量子表示相对于经典协方差表示具有纠缠增加数据之间相关性的优势。让我给你一个例子来说明这一点。
假设我们有两个量子比特,表示为|0〉和|1〉。经典的协方差表示只能表示两个向量之间的线性相关性,例如协方差矩阵可以衡量它们之间的协方差和相关性。然而,经典表示无法捕捉到更高级别的关联,例如非线性关系。
而在量子表示中,量子比特之间可以处于纠缠态,这意味着它们之间存在非经典的相互关联。通过纠缠,量子信息处理器可以捕捉到数据之间更复杂的关系和统计特性。
举个例子,假设我们有两个量子比特,它们的状态可以表示为:
|ψ〉 = (1/√2)(|00〉 + |11〉)
这个纠缠态表示了两个量子比特之间的关联。当我们对其中一个量子比特进行测量时,另一个量子比特的状态也会立即塌缩到相应的测量结果。这种纠缠关系可以用来捕捉数据之间的相关性和统计特性。
在生成对抗学习任务中,量子信息处理器可以利用纠缠来增强生成器和判别器之间的交互和学习能力。纠缠可以帮助生成器网络更好地模拟真实数据的分布,并使得判别器网络更有效地区分生成的样本和真实数据。通过利用纠缠,量子信息处理器可以提供更丰富和复杂的生成对抗学习任务的版本。
需要注意的是,纠缠的利用需要设计合适的量子算法和量子电路,以及适当的量子态编码和纠缠操作。在实际应用中,如何利用纠缠来增强生成对抗学习任务的性能仍然是一个活跃的研究领域。
相关文章:

量子信息处理器可能能够提供高度压缩的生成对抗学习任务的版本
量子信息处理在生成对抗学习任务中的应用可能性,以及量子信息处理器在表示高维向量和执行线性代数运算上的优势。 举个例子 假设底层数据由M个在N维实数或复数空间中的归一化向量~vj组成,使得数据的(归一化)协方差矩阵为C (1/M…...
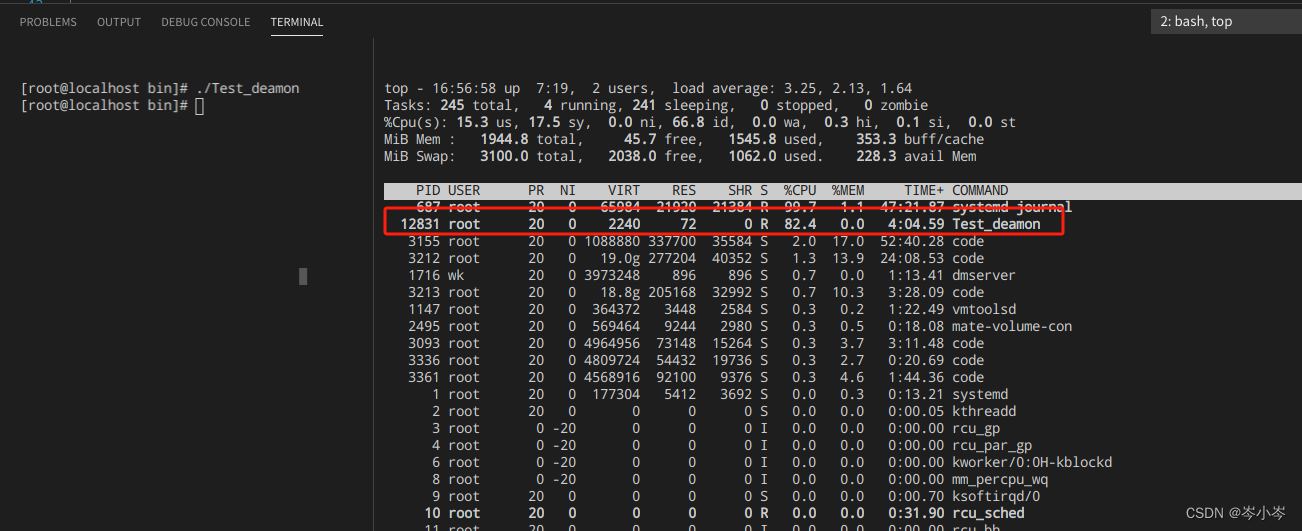
linux-守护进程daemon
linux-守护进程daemon 代码实现 main.c运行结果 代码实现 main.c //pName:程序名 //facility: 守护进程,输出日志类型 302页 #include<signal.h> #include<syslog.h> #include<fcntl.h> static int daemon_proc 0; #defin…...

Kafka Tool(Kafka 可视化工具)安装及使用教程
Kafka Tool(Kafka 可视化工具)安装及使用教程 Kafka Tool 工具下载 下载地址 http://www.kafkatool.com/download.html 下载界面 不同版本的Kafka对应不同版本的工具,个人使用的是2.11,所以下载的是最新的2.0.8版本ÿ…...

【大揭秘】美团面试题:ConcurrentHashMap和Hashtable有什么区别?一文解析!
正文 亲爱的小伙伴们,大家好!我是小米,一个热爱技术分享的程序员,今天我为大家带来了一篇有关美团面试题的热门话题:ConcurrentHashMap 和 Hashtable 有什么区别。这个问题在Java面试中常常被拿来考察对多线程编程的理…...
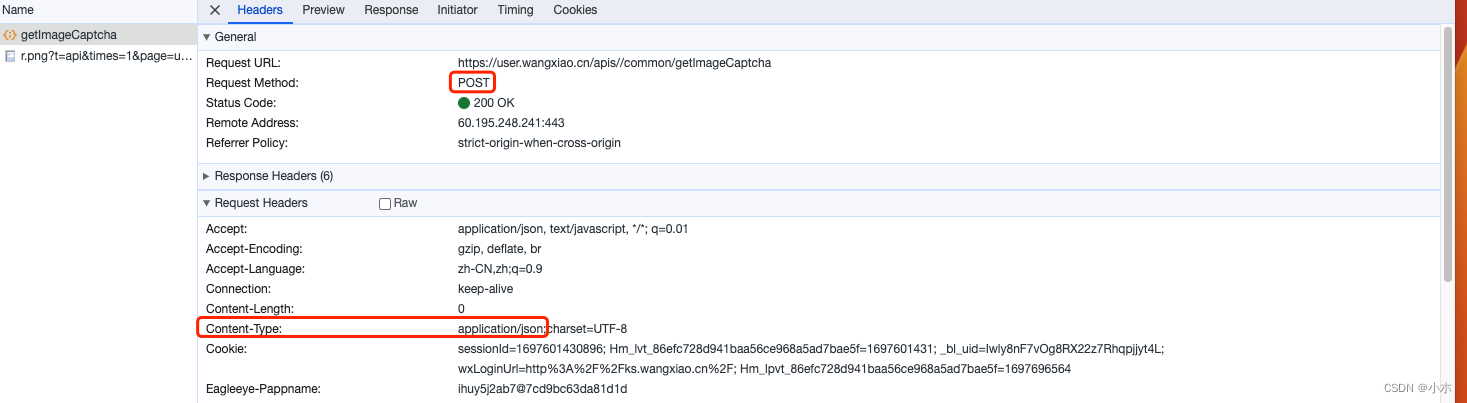
爬虫基础 JS逆向
爬虫核心 1. HTTP协议与WEB开发 1. 什么是请求头请求体,响应头响应体 2. URL地址包括什么 3. get请求和post请求到底是什么 4. Content-Type是什么 (1)简介 HTTP协议是Hyper Text Transfer Protocol(超文本传输协议)…...

nextTick实现原理
答题思路: 此题实际考查vue异步更新策略说出vue是怎么通过异步、批量的方式更新以提高性能的最后把源码中实现说一下 回答范例: vue有个批量、异步更新策略,数据变化时,vue开启一个队列,并缓冲在同一事件循环中发生的…...

CentOS 7中安装ZooKeeper
文章目录 下载解压安装环境变量配置文件启动设置开机自启动开放端口 CentOS 7.6 ZooKeeper 3.5.7 本文介绍了如何在CentOS 7系统中安装单机版的ZooKeeper。 下载 点击官网下载 解压安装 # 解压 tar -xzvf apache-zookeeper-3.5.7-bin.tar.gz sudo mv apache-zookeeper-3.5.…...

推荐《幽游白书》
《幽游白书》是日本漫画家富坚义博于1990年12月3日—1994年7月25日于集英社旗下杂志《周刊少年Jump》上连载的少年漫画作品,全175话(含外传一话)。现时发行的单行本共计19册,电子版由漫番漫画、哔哩哔哩漫画发布 [1-2] 。 本作最…...

Linux MMC子系统 - 1.eMMC简介
By: Ailson Jack Date: 2023.10.21 个人博客:http://www.only2fire.com/ 本文在我博客的地址是:http://www.only2fire.com/archives/160.html,排版更好,便于学习,也可以去我博客逛逛,兴许有你想要的内容呢。…...
聊聊Android线程优化这件事
一、背景 在日常开发APP的过程中,难免需要使用第二方库和第三方库来帮助开发者快速实现一些功能,提高开发效率。但是,这些库也可能会给线程带来一定的压力,主要表现在以下几个方面: 线程数量增多:一些库可…...

Linux性能优化--实用工具:性能工具助手
8.0 概述 本章介绍一些在Linux系统上可用的实用程序,它们能够加强性能工具的有效性和可用性。实用工具本身不是性能工具,但是当它们与性能工具一起使用时,它们可以帮助完成如下功能:自动执行繁琐的任务、分析性能统计数据&#x…...

[PyTorch]即插即用的热力图生成
先上张效果图,本来打算移植霹雳老师的使用Pytorch实现Grad-CAM并绘制热力图。但是看了下代码,需要骨干网络按照标准写法(即将特征层封装为features数组),而我写的网络图省事并没有进行封装,改造网络的代价又…...

golang笔记18--go并发多线程
golang笔记18--go并发多线程 介绍核心用法MutexRWMutexWaitGroupCondOncemapPoolContextselect 注意事项参考文档 介绍 大家都知道go语言近年来越来越火了,其中有一个要点是go语言在并发场景有很高的性能,比如可以通过启动很多个 goroutine 来执行并发任…...

使用OkHttp和Java来下载
以下是一个使用OkHttp和Java来下载内容的下载器程序,同时使用了jshk.com.cn/get_proxy来获取代理服务器。请注意,为了简化代码,我们将忽略一些异常处理和安全性检查。 import java.io.File;import java.io.FileOutputStream;import java.io.I…...

HttpServlet源码分析及HttpServletRequest接口
2023.10.20 HttpServlet HttpServlet类是专门为HTTP协议准备的。比GenericServlet更加适合HTTP协议下的开发。 http包下都有哪些类和接口呢?(jakarta.servlet.http.*) jakarta.servlet.http.HttpServlet (HTTP协议专用的Servlet…...

CENTOS 7基于ISO文件进行安装新软件
众所周知,YUM是CENTOS7的安装程序。 普通情况下,连网之后 ,用yum install 就可以安装。 但当网络环境经常出现连接失败的情况,默认情况下的行为就走不通了。 为解决这个问题,可以考虑如下三个方案 方案一:Y…...
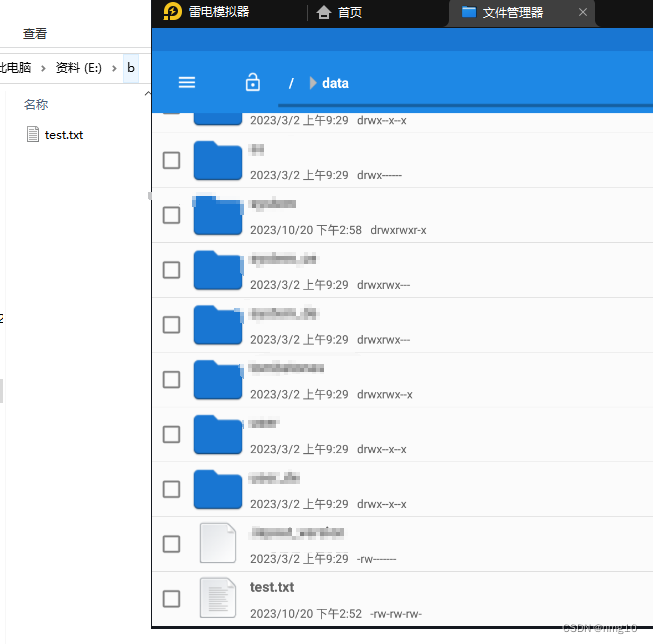
模拟器-雷电-使用adb push或adb pull操作文件
一、环境 windows 10 雷电模拟器4.0.83 二、问题 有时候我们会需要往模拟器拷贝文件或者复制文件到我的电脑 三、方法 1、获取root权限 adb root adb remount 有可能遇到【daemon not running; starting now at tcp:5037】的报错 查看端口占用进程:netstat -…...

【前端设计模式】之命令模式
引言 命令设计模式是一种行为型设计模式,它允许你将命令封装到一个对象中,从而使你可以参数化不同的请求,以及存储、排队、重播和撤销请求。这种设计模式在处理用户界面操作、远程网络请求或其他需要异步执行的操作时非常有用。在前端开发中…...

用c++写一个高精度计算的乘法运算
这段代码是一个用C编写的程序,它实现了两个大整数的乘法运算。 #include<iostream> #include<cstdio> #include<cstring> using namespace std;int main(){char a1[101]"222",b1[101]"2";int a[101],b[101],c[10001],lena,l…...
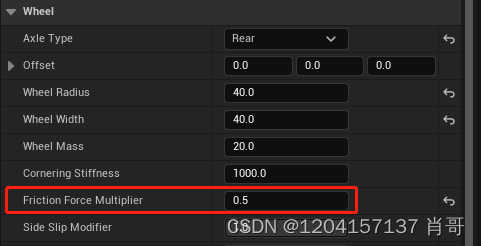
UE5 ChaosVehicles载具 实现大漂移 (连载四)
载具设置成前驱模式 前轮摩擦力倍增x5 后轮摩擦力倍增x0.5...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
