C++前缀和算法的应用:从仓库到码头运输箱子原理、源码、测试用例
本文涉及的基础知识点
C++算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频
双指针
单调双向队列
题目
你有一辆货运卡车,你需要用这一辆车把一些箱子从仓库运送到码头。这辆卡车每次运输有 箱子数目的限制 和 总重量的限制 。
给你一个箱子数组 boxes 和三个整数 portsCount, maxBoxes 和 maxWeight ,其中 boxes[i] = [portsi, weighti] 。
portsi 表示第 i 个箱子需要送达的码头, weightsi 是第 i 个箱子的重量。
portsCount 是码头的数目。
maxBoxes 和 maxWeight 分别是卡车每趟运输箱子数目和重量的限制。
箱子需要按照 数组顺序 运输,同时每次运输需要遵循以下步骤:
卡车从 boxes 队列中按顺序取出若干个箱子,但不能违反 maxBoxes 和 maxWeight 限制。
对于在卡车上的箱子,我们需要 按顺序 处理它们,卡车会通过 一趟行程 将最前面的箱子送到目的地码头并卸货。如果卡车已经在对应的码头,那么不需要 额外行程 ,箱子也会立马被卸货。
卡车上所有箱子都被卸货后,卡车需要 一趟行程 回到仓库,从箱子队列里再取出一些箱子。
卡车在将所有箱子运输并卸货后,最后必须回到仓库。
请你返回将所有箱子送到相应码头的 最少行程 次数。
示例 1:
输入:boxes = [[1,1],[2,1],[1,1]], portsCount = 2, maxBoxes = 3, maxWeight = 3
输出:4
解释:最优策略如下:
- 卡车将所有箱子装上车,到达码头 1 ,然后去码头 2 ,然后再回到码头 1 ,最后回到仓库,总共需要 4 趟行程。
所以总行程数为 4 。
注意到第一个和第三个箱子不能同时被卸货,因为箱子需要按顺序处理(也就是第二个箱子需要先被送到码头 2 ,然后才能处理第三个箱子)。
示例 2:
输入:boxes = [[1,2],[3,3],[3,1],[3,1],[2,4]], portsCount = 3, maxBoxes = 3, maxWeight = 6
输出:6
解释:最优策略如下: - 卡车首先运输第一个箱子,到达码头 1 ,然后回到仓库,总共 2 趟行程。
- 卡车运输第二、第三、第四个箱子,到达码头 3 ,然后回到仓库,总共 2 趟行程。
- 卡车运输第五个箱子,到达码头 2 ,回到仓库,总共 2 趟行程。
总行程数为 2 + 2 + 2 = 6 。
示例 3:
输入:boxes = [[1,4],[1,2],[2,1],[2,1],[3,2],[3,4]], portsCount = 3, maxBoxes = 6, maxWeight = 7
输出:6
解释:最优策略如下: - 卡车运输第一和第二个箱子,到达码头 1 ,然后回到仓库,总共 2 趟行程。
- 卡车运输第三和第四个箱子,到达码头 2 ,然后回到仓库,总共 2 趟行程。
- 卡车运输第五和第六个箱子,到达码头 3 ,然后回到仓库,总共 2 趟行程。
总行程数为 2 + 2 + 2 = 6 。
示例 4:
输入:boxes = [[2,4],[2,5],[3,1],[3,2],[3,7],[3,1],[4,4],[1,3],[5,2]], portsCount = 5, maxBoxes = 5, maxWeight = 7
输出:14
解释:最优策略如下: - 卡车运输第一个箱子,到达码头 2 ,然后回到仓库,总共 2 趟行程。
- 卡车运输第二个箱子,到达码头 2 ,然后回到仓库,总共 2 趟行程。
- 卡车运输第三和第四个箱子,到达码头 3 ,然后回到仓库,总共 2 趟行程。
- 卡车运输第五个箱子,到达码头 3 ,然后回到仓库,总共 2 趟行程。
- 卡车运输第六和第七个箱子,到达码头 3 ,然后去码头 4 ,然后回到仓库,总共 3 趟行程。
- 卡车运输第八和第九个箱子,到达码头 1 ,然后去码头 5 ,然后回到仓库,总共 3 趟行程。
总行程数为 2 + 2 + 2 + 2 + 3 + 3 = 14 。
提示:
1 <= boxes.length <= 105
1 <= portsCount, maxBoxes, maxWeight <= 105
1 <= portsi <= portsCount
1 <= weightsi <= maxWeight
可理解行强的解法
如果有多种运输的boxs[0,i)的方式,只需要保留行程最少的方式,且只需要记录最小行程,此值用m_vRet[i]记录。分成两步:第一步,运输box[0,j),第二步运输[j,i)。一次可以运输完成,可以看成第一步是box[0,0)。枚举i,j的时间复杂度都是O(n),总时间复杂度是O(n*n)。
利用前缀和计算[j,i)的箱子总重量
vWeightSum[i],记录了boxs[0,i)的重中立,vWeightSum[i]-vWeightSum[j]。
利用前缀和计算[i,j)需要单独下车的次数
vDownSum[i]记录[0,i)需要单独下车的次数。vDown[j]-vDownSum[i]。和前面的箱子不同,则需要单独下车。
优化枚举
m_vRet[i] = min(…,X) X=m_vRet[j]+1 + 1 + vDown[j+1,i)。 1+1 表示返程和下第一箱子,从第二个箱子起要计算要单独下。X = m_vRet[j]+1+1+vDown[i] - vDown[j+1] ,令 Y= m_vRet[j]-vDow[j+1],则X=Y + 2 + vDown[i] ,显然Y可以提前计算。每次处理完i,将Y记录到setPre中。setPre对应的索引为[left,i),如果[left,i)超量或超重,则left++,并更新setPre。
时间复杂度
枚举i,时间复杂度。二分查找setPre,时间复杂度O(logn),总时间复杂度O(nlogn)。
核心代码
class Solution {
public:
int boxDelivering(vector<vector>& boxes, int portsCount, int maxBoxes, int maxWeight) {
m_c = boxes.size();
m_vRet.resize(m_c+1);//记录boxes[0,i) 需的最小行程数
vector vWeightSum = { 0 };//箱子重量前缀和
for (const auto& v : boxes)
{
vWeightSum.emplace_back(v[1] + vWeightSum.back());
}
vector vDownSum = { 0,0 };//假定不是本车的第一个箱子,卸货需要的次数
for (int i = 1; i < m_c; i++)
{
vDownSum.emplace_back(vDownSum.back() + (boxes[i][0] != boxes[i-1][0]));
}
std::multiset setPre = { 0 }; //记录可以作为前一趟的最小行程数-vDownSum[i + 1]
int left = 0;//[left,i)是上一趟的行程
for (int i = 1; i <= m_c; i++)
{
// [left,i)为空,不会超重,也不会超量。所以无需判断是否为空
while ((i - left > maxBoxes) || (vWeightSum[i] - vWeightSum[left] > maxWeight))
{
//如果[left,i)超重或超亮
const int tmp = m_vRet[left ] - vDownSum[left+1 ];
setPre.erase(setPre.find(tmp));
left++;
}
m_vRet[i ] = *setPre.begin() + 2 + vDownSum[i] ;
if (i + 1 <= m_c)
{
setPre.emplace(m_vRet[i] - vDownSum[i + 1]);
}
}
return m_vRet.back();
}
int m_c;
vector m_vRet;
};
测试用例
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
int main()
{
vector<vector> boxes = { {1,1},{2,1},{1,1} };
int portsCount = 2, maxBoxes = 3, maxWeight = 3;
auto res = Solution().boxDelivering(boxes, portsCount, maxBoxes, maxWeight);
Assert(4, res);
boxes = { {1,2},{3,3},{3,1},{3,1},{2,4} };
portsCount = 3, maxBoxes = 3, maxWeight =6;
res = Solution().boxDelivering(boxes, portsCount, maxBoxes, maxWeight);
Assert(6, res);
boxes = { {2,4},{2,5},{3,1},{3,2},{3,7},{3,1},{4,4},{1,3},{5,2} };
portsCount = 5, maxBoxes = 5, maxWeight = 7;
res = Solution().boxDelivering(boxes, portsCount, maxBoxes, maxWeight);
Assert(14, res);
//CConsole::Out(res);
}
优化二:单调双向队列
原理
setPre的旧值如果大于等于新值,则被淘汰了。这意味着值是按升序排序的。移除值有两种原因:一,旧值比新值大,被淘汰。从容器尾淘汰。二,旧值超重或超过数量了,从容器头淘汰。所以用双向队列。
代码
class Solution {
public:
int boxDelivering(vector<vector>& boxes, int portsCount, int maxBoxes, int maxWeight) {
m_c = boxes.size();
m_vRet.resize(m_c+1);//记录boxes[0,i) 需的最小行程数
vector vWeightSum = { 0 };//箱子重量前缀和
for (const auto& v : boxes)
{
vWeightSum.emplace_back(v[1] + vWeightSum.back());
}
vector vDownSum = { 0,0 };//假定不是本车的第一个箱子,卸货需要的次数
for (int i = 1; i < m_c; i++)
{
vDownSum.emplace_back(vDownSum.back() + (boxes[i][0] != boxes[i-1][0]));
}
std::deque<pair<int, int>> mSumJ = { { 0,0} };
for (int i = 1; i <= m_c; i++)
{
// [left,i)为空,不会超重,也不会超量。所以无需判断是否为空
while (mSumJ.size() &&((i - mSumJ.front().second > maxBoxes) || (vWeightSum[i] - vWeightSum[mSumJ.front().second] > maxWeight)))
{
//如果[left,i)超重或超亮
mSumJ.pop_front();
}
m_vRet[i ] = mSumJ.front().first + 2 + vDownSum[i] ;
if (i + 1 > m_c)
{
continue;
}
const int iNew = m_vRet[i] - vDownSum[i + 1];
while (mSumJ.size() && (mSumJ.back().first >= iNew))
{
mSumJ.pop_back();
}
mSumJ.emplace_back(iNew, i);
}
return m_vRet.back();
}
int m_c;
vector m_vRet;
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 鄙人想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨家名称的来源:有所得以墨记之。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境:
VS2022 C++17

相关文章:

C++前缀和算法的应用:从仓库到码头运输箱子原理、源码、测试用例
本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 双指针 单调双向队列 题目 你有一辆货运卡车,你需要用这一辆车把一些箱子从仓库运送到码头。这辆卡车每次运输有 箱子数目的限制 和 总重量的限制 。 给你…...
【面试HOT100】链表树
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于LeetCodeHot100进行的,每个知识点的修正和深入主要参考…...
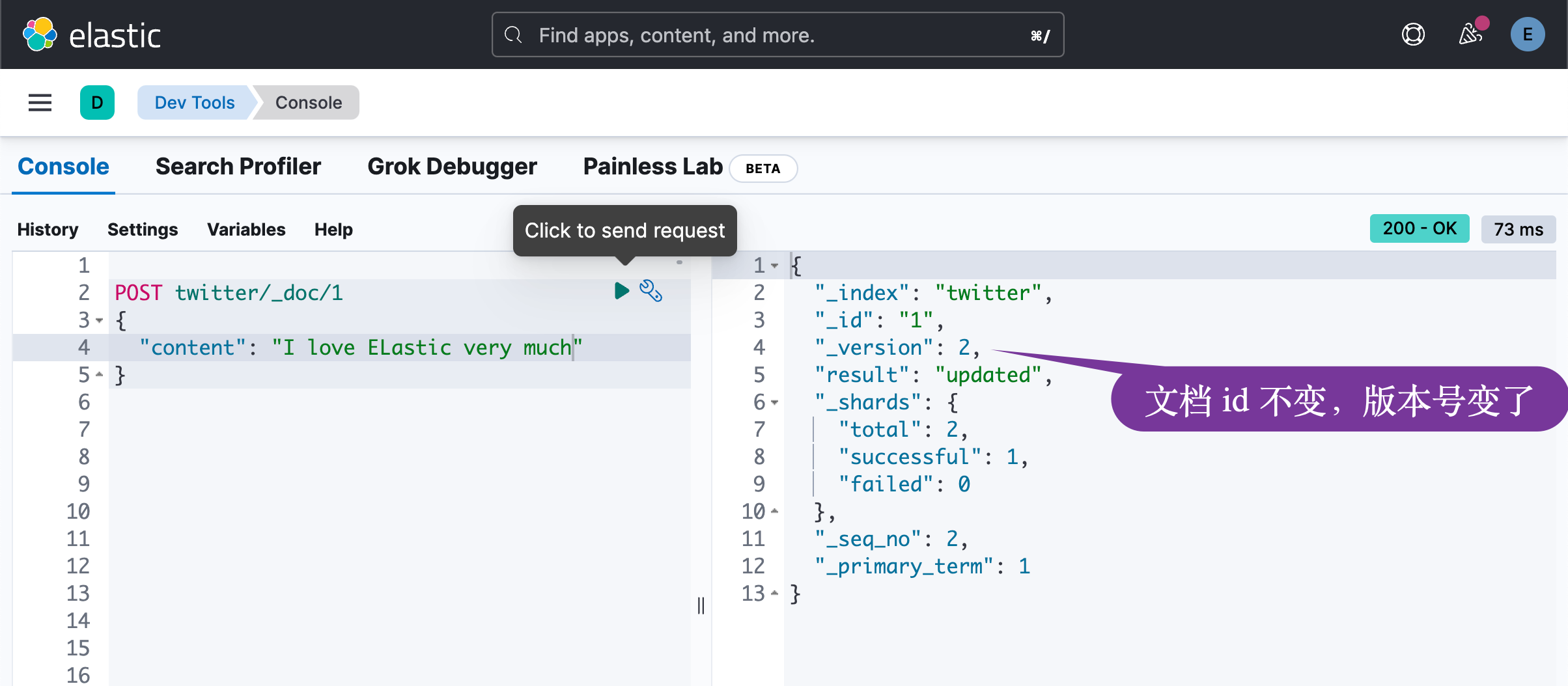
了解 Elasticsearch 自动生成的文档 _id:重复是一个问题吗?
Elasticsearch 中自动生成的文档 ID 当你在未指定 ID 的情况下对文档建立索引时,Elasticsearch 会自动为该文档生成唯一的 ID。 该 ID 是 Base64 编码的 UUID,由多个部分组成,每个部分都有特定的用途。 ID 生成过程针对索引速度和存储效率进…...

量子信息处理器可能能够提供高度压缩的生成对抗学习任务的版本
量子信息处理在生成对抗学习任务中的应用可能性,以及量子信息处理器在表示高维向量和执行线性代数运算上的优势。 举个例子 假设底层数据由M个在N维实数或复数空间中的归一化向量~vj组成,使得数据的(归一化)协方差矩阵为C (1/M…...
linux-守护进程daemon
linux-守护进程daemon 代码实现 main.c运行结果 代码实现 main.c //pName:程序名 //facility: 守护进程,输出日志类型 302页 #include<signal.h> #include<syslog.h> #include<fcntl.h> static int daemon_proc 0; #defin…...

Kafka Tool(Kafka 可视化工具)安装及使用教程
Kafka Tool(Kafka 可视化工具)安装及使用教程 Kafka Tool 工具下载 下载地址 http://www.kafkatool.com/download.html 下载界面 不同版本的Kafka对应不同版本的工具,个人使用的是2.11,所以下载的是最新的2.0.8版本ÿ…...

【大揭秘】美团面试题:ConcurrentHashMap和Hashtable有什么区别?一文解析!
正文 亲爱的小伙伴们,大家好!我是小米,一个热爱技术分享的程序员,今天我为大家带来了一篇有关美团面试题的热门话题:ConcurrentHashMap 和 Hashtable 有什么区别。这个问题在Java面试中常常被拿来考察对多线程编程的理…...
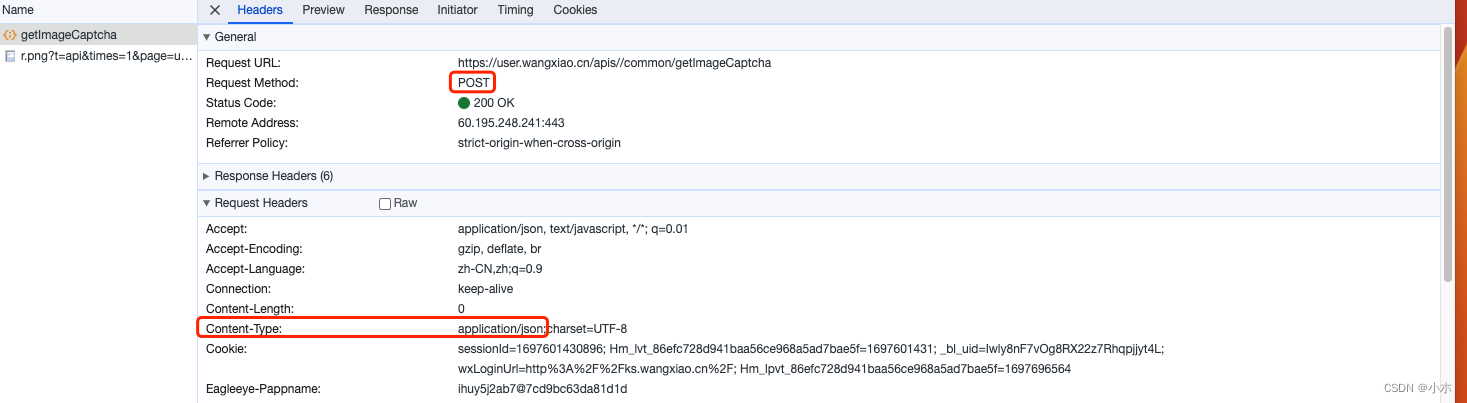
爬虫基础 JS逆向
爬虫核心 1. HTTP协议与WEB开发 1. 什么是请求头请求体,响应头响应体 2. URL地址包括什么 3. get请求和post请求到底是什么 4. Content-Type是什么 (1)简介 HTTP协议是Hyper Text Transfer Protocol(超文本传输协议)…...

nextTick实现原理
答题思路: 此题实际考查vue异步更新策略说出vue是怎么通过异步、批量的方式更新以提高性能的最后把源码中实现说一下 回答范例: vue有个批量、异步更新策略,数据变化时,vue开启一个队列,并缓冲在同一事件循环中发生的…...

CentOS 7中安装ZooKeeper
文章目录 下载解压安装环境变量配置文件启动设置开机自启动开放端口 CentOS 7.6 ZooKeeper 3.5.7 本文介绍了如何在CentOS 7系统中安装单机版的ZooKeeper。 下载 点击官网下载 解压安装 # 解压 tar -xzvf apache-zookeeper-3.5.7-bin.tar.gz sudo mv apache-zookeeper-3.5.…...

推荐《幽游白书》
《幽游白书》是日本漫画家富坚义博于1990年12月3日—1994年7月25日于集英社旗下杂志《周刊少年Jump》上连载的少年漫画作品,全175话(含外传一话)。现时发行的单行本共计19册,电子版由漫番漫画、哔哩哔哩漫画发布 [1-2] 。 本作最…...

Linux MMC子系统 - 1.eMMC简介
By: Ailson Jack Date: 2023.10.21 个人博客:http://www.only2fire.com/ 本文在我博客的地址是:http://www.only2fire.com/archives/160.html,排版更好,便于学习,也可以去我博客逛逛,兴许有你想要的内容呢。…...
聊聊Android线程优化这件事
一、背景 在日常开发APP的过程中,难免需要使用第二方库和第三方库来帮助开发者快速实现一些功能,提高开发效率。但是,这些库也可能会给线程带来一定的压力,主要表现在以下几个方面: 线程数量增多:一些库可…...

Linux性能优化--实用工具:性能工具助手
8.0 概述 本章介绍一些在Linux系统上可用的实用程序,它们能够加强性能工具的有效性和可用性。实用工具本身不是性能工具,但是当它们与性能工具一起使用时,它们可以帮助完成如下功能:自动执行繁琐的任务、分析性能统计数据&#x…...

[PyTorch]即插即用的热力图生成
先上张效果图,本来打算移植霹雳老师的使用Pytorch实现Grad-CAM并绘制热力图。但是看了下代码,需要骨干网络按照标准写法(即将特征层封装为features数组),而我写的网络图省事并没有进行封装,改造网络的代价又…...

golang笔记18--go并发多线程
golang笔记18--go并发多线程 介绍核心用法MutexRWMutexWaitGroupCondOncemapPoolContextselect 注意事项参考文档 介绍 大家都知道go语言近年来越来越火了,其中有一个要点是go语言在并发场景有很高的性能,比如可以通过启动很多个 goroutine 来执行并发任…...

使用OkHttp和Java来下载
以下是一个使用OkHttp和Java来下载内容的下载器程序,同时使用了jshk.com.cn/get_proxy来获取代理服务器。请注意,为了简化代码,我们将忽略一些异常处理和安全性检查。 import java.io.File;import java.io.FileOutputStream;import java.io.I…...

HttpServlet源码分析及HttpServletRequest接口
2023.10.20 HttpServlet HttpServlet类是专门为HTTP协议准备的。比GenericServlet更加适合HTTP协议下的开发。 http包下都有哪些类和接口呢?(jakarta.servlet.http.*) jakarta.servlet.http.HttpServlet (HTTP协议专用的Servlet…...

CENTOS 7基于ISO文件进行安装新软件
众所周知,YUM是CENTOS7的安装程序。 普通情况下,连网之后 ,用yum install 就可以安装。 但当网络环境经常出现连接失败的情况,默认情况下的行为就走不通了。 为解决这个问题,可以考虑如下三个方案 方案一:Y…...
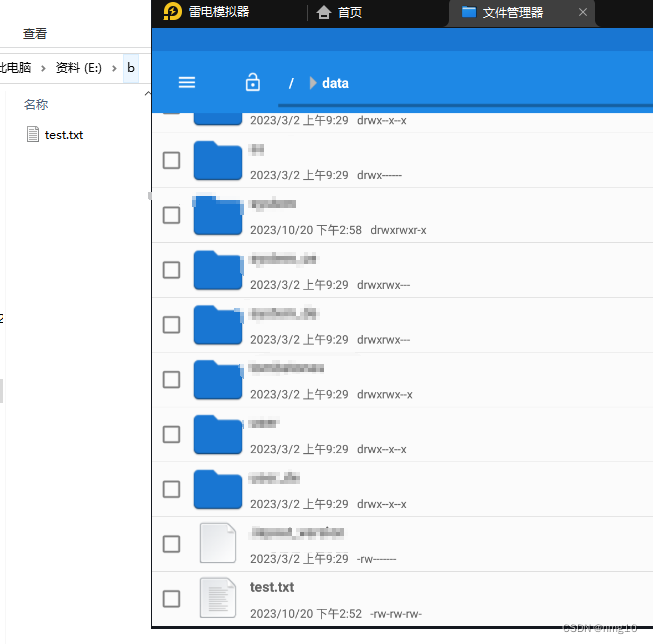
模拟器-雷电-使用adb push或adb pull操作文件
一、环境 windows 10 雷电模拟器4.0.83 二、问题 有时候我们会需要往模拟器拷贝文件或者复制文件到我的电脑 三、方法 1、获取root权限 adb root adb remount 有可能遇到【daemon not running; starting now at tcp:5037】的报错 查看端口占用进程:netstat -…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
