【动态规划】583. 两个字符串的删除操作、72. 编辑距离
提示:努力生活,开心、快乐的一天
文章目录
- 583. 两个字符串的删除操作
- 💡解题思路
- 🤔遇到的问题
- 💻代码实现
- 🎯题目总结
- 72. 编辑距离
- 💡解题思路
- 🤔遇到的问题
- 💻代码实现
- 🎯题目总结
- 🎈今日心得
583. 两个字符串的删除操作
题目链接:583. 两个字符串的删除操作
💡解题思路
- 本题和动态规划:115.不同的子序列 (opens new window)相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的
- 动规五部曲
- 确定dp数组以及下标的含义:dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
- 确定递推公式:主要就是两大情况: word1[i - 1] 与 word2[j - 1]相同,word1[i - 1] 与 word2[j - 1]不相同
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
所以递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。 - dp数组如何初始化:dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
同理dp[0][j] = j - 确定遍历顺序:从递推公式,可以看出,有三个方向可以推出dp[i][j]
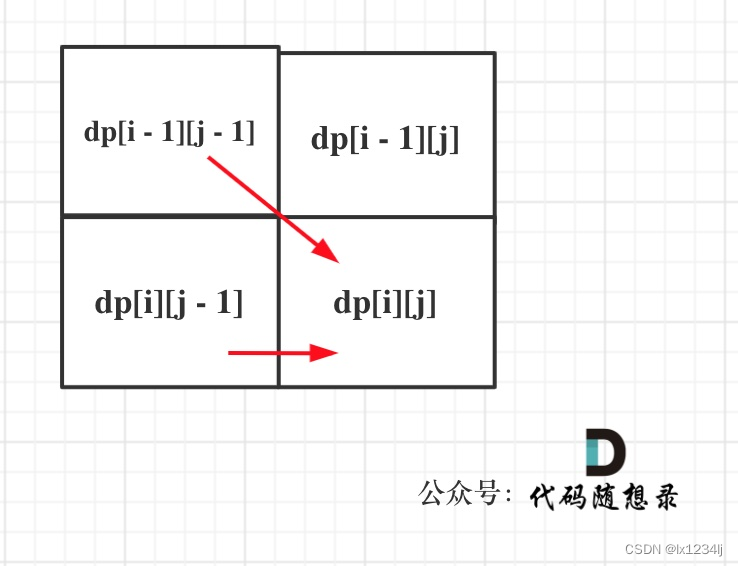
- 举例推导dp数组:按照递推公式推导一下做推导,如果发现结果不对,就把dp数组打印出来
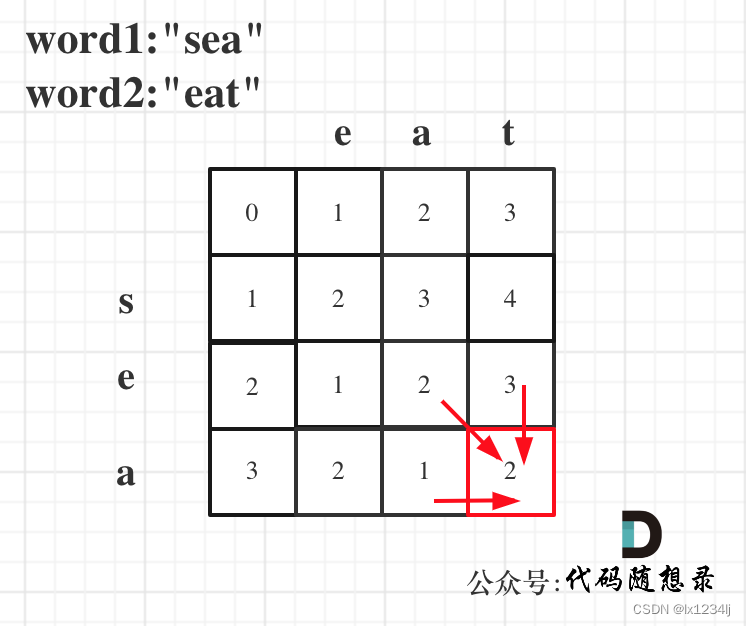
🤔遇到的问题
- 注意初始化
💻代码实现
动态规划
var minDistance = function(word1, word2) {//dp[i][j],以i-1结尾的word1和以j-1结尾的word2,想要达到相等,所需要删除元素的最少次数。let w1 = word1.lengthlet w2 = word2.lengthlet dp = new Array(w1 + 1).fill(0).map(x => new Array(w2 + 1).fill(0))//初始化//word2为空字符串for (let i = 0; i <= w1; i++){dp[i][0] = i}//word1为空字符串for (let j = 0; j <= w2; j++){dp[0][j] = j}for (let i = 1; i <= w1; i++){for (let j = 1; j <= w2; j++){if (word1[i - 1] === word2[j - 1]) {dp[i][j] = dp[i-1][j-1]} else {dp[i][j] = Math.min(dp[i-1][j]+1,dp[i][j-1]+1)}}}console.log(dp)return dp[w1][w2]
};
🎯题目总结
特别注意的是:此题两个字符床都可以进行删除,所以在初始化和递推公式都会与之前有所不同,需要特别注意
72. 编辑距离
题目链接:72. 编辑距离
💡解题思路
- 动规五部曲
- 确定dp数组以及下标的含义:dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]
- 确定递推公式:要考虑清楚编辑的几种操作,4种情况
if (word1[i - 1] == word2[j - 1])不操作
if (word1[i - 1] != word2[j - 1])增删换
情况1: if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];根据dp[i][j]的定义,word1[i - 1] 与 word2[j - 1]相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是 dp[i][j]了。
情况2:if (word1[i - 1] != word2[j - 1])时
1、操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。即 dp[i][j] = dp[i - 1][j] + 1;
2、操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。即 dp[i][j] = dp[i][j - 1] + 1;
注意:word2添加一个元素,相当于word1删除一个元素,例如 word1 = “ad” ,word2 = “a”,word1删除元素’d’ 和 word2添加一个元素’d’,变成word1=“a”, word2=“ad”, 最终的操作数是一样!
3、操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
- dp数组如何初始化:
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;同理dp[0][j] = j; - 确定遍历顺序:dp[i][j]是依赖左方,上方和左上方元素的
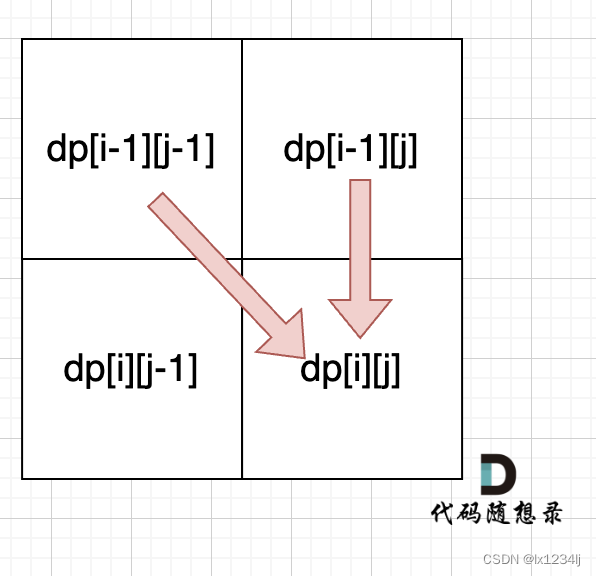
- 举例推导dp数组:按照递推公式推导一下做推导,如果发现结果不对,就把dp数组打印出来
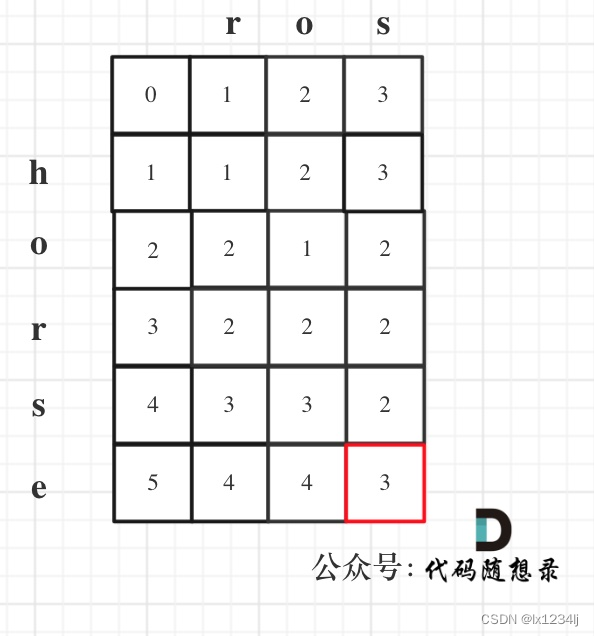
🤔遇到的问题
- word1[i - 1] != word2[j - 1时的三种情况的分析
💻代码实现
动态规划
var minDistance = function(word1, word2) {let w1 = word1.lengthlet w2 = word2.lengthlet dp = new Array(w1 + 1).fill(0).map(x => new Array(w2 + 1).fill(0))for (let i = 0; i <= w1; i++){dp[i][0] = i}for (let j = 0; j <= w2; j++){dp[0][j] = j}for (let i = 1; i <= w1; i++){for (let j = 1; j <= w2; j++){if (word1[i - 1] === word2[j - 1]) {dp[i][j] = dp[i-1][j-1]} else {dp[i][j] = Math.min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1}}}return dp[w1][w2]
};
🎯题目总结
if (word1[i - 1] != word2[j - 1])时
1、操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。即 dp[i][j] = dp[i - 1][j] + 1;
2、操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。即 dp[i][j] = dp[i][j - 1] + 1;
注意:word2添加一个元素,相当于word1删除一个元素,例如 word1 = “ad” ,word2 = “a”,word1删除元素’d’ 和 word2添加一个元素’d’,变成word1=“a”, word2=“ad”, 最终的操作数是一样!
3、操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
🎈今日心得
编辑距离的题目终于达到了最难的一题,确实难
相关文章:

【动态规划】583. 两个字符串的删除操作、72. 编辑距离
提示:努力生活,开心、快乐的一天 文章目录 583. 两个字符串的删除操作💡解题思路🤔遇到的问题💻代码实现🎯题目总结 72. 编辑距离💡解题思路🤔遇到的问题💻代码实现&…...
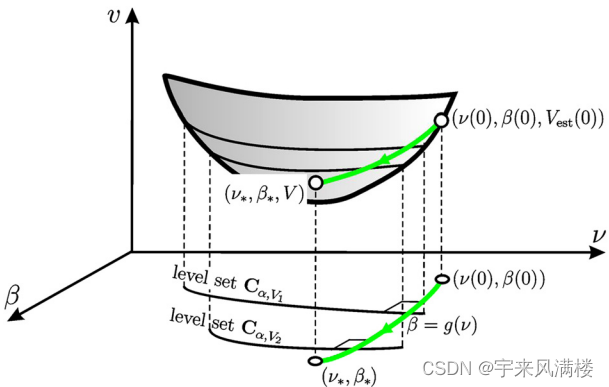
Gradient conjugate priors and multi-layer neural networks
动机 先验参数 m , α , β , v m,\alpha,\beta,v m,α,β,v和随机变量 τ \tau τ KL散度的形式是: Dynamics of m , α , β , v m,\alpha,\beta,v m,α,β,v Dynamics of m , β , v m,\beta,v m,β,v for a fixed α \alpha α 绿色轨迹连接初始点和目标点…...

DistributedDataParallel数据不均衡
背景 在使用 DistributedDataParallel 进行数据并行训练时,每次反向传播都需要执行 all_reduce 操作以同步各个进程的梯度。all_reduce 需要进程组中的所有进程参与,如果某一个进程没有执行 all_reduce(一个进程的输入较其他进程少ÿ…...
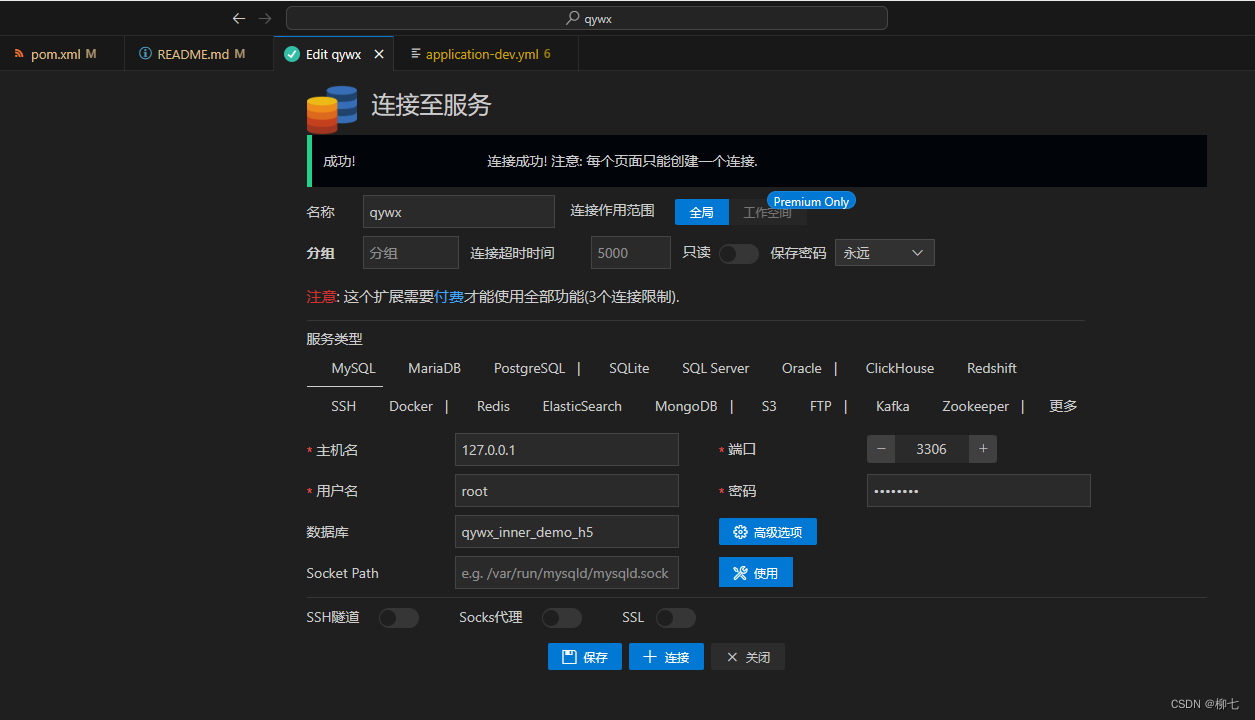
Cloud Studio连接MySQL,Access denied for一系列问题
官方文档有写如何安装Mysql $ apt update $ apt install mysql-server mysql-client -y$ service mysql start mysql -uroot -p123456进入MySQL命令行 问题出在连接数据库这一步,命令行能进去,但是数据库插件和代码都连不上 Access denied for 大概率…...
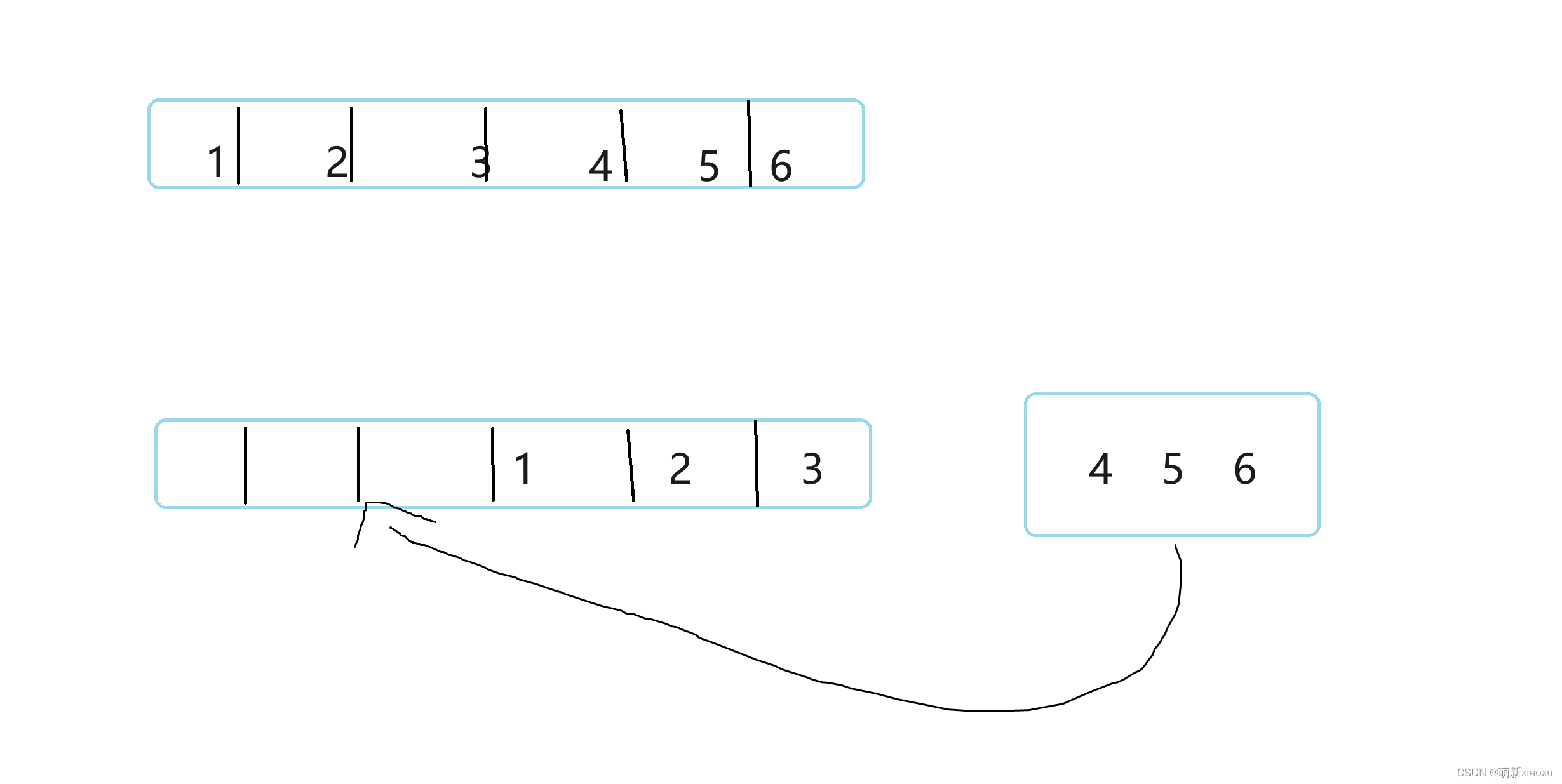
经典题型---旋转数组
经典题型—旋转数组 文章目录 经典题型---旋转数组一、题目二、代码实现 一、题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步…...

vue如何实现登录数据的持久化
Vue.js是一款流行的JavaScript框架,它可以帮助开发者构建高效且易于维护的单页面应用程序。在Vue.js中,实现登录数据的持久化是一个重要的任务,因为它可以帮助用户保持登录状态并避免频繁的登录操作。在本文中,我们将讨论Vue.js如…...
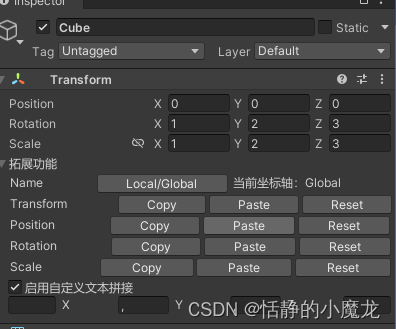
【Unity3D编辑器开发】Unity3D中实现Transform组件拓展,快速复制、粘贴、复原【非常实用】
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址我的个人博客 大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 在开发中,常常会遇到频繁复制粘贴物体的坐标、旋转…...

求解仿射变换矩阵
仿射变换是图形学中经常用到的方法,通常但是仿射变换的系数是未知的,需要找到变换前后的三对对应点进行求解。 from affine import Affine import numpy as np参考文献 矩阵最小二乘法求解仿射变换矩阵 def solve_affine(init_points, goal_points) -&…...

【每日一题】—— 最大素因子
🌏博客主页:PH_modest的博客主页 🚩当前专栏:每日一题 💌其他专栏: 🔴 每日反刍 🟡 C跬步积累 🟢 C语言跬步积累 🌈座右铭:广积粮,缓称…...
【JavaEE】JUC 常见的类 -- 多线程篇(8)
JUC 常见的类 1. Callable 接口2. ReentrantLock3. 原子类4. 线程池5. 信号量 Semaphore6. CountDownLatch 1. Callable 接口 Callable Interface 也是一种创建线程的方式 Runnable 能表示一个任务 (run方法) – 返回 voidCallable 也能表示一个任务(call方法) 返回一个具体的…...

java项目运行时信息获取
大体思路如下,想要获取启动时处理器数量、jvm 相关信息,操作系统信息、运行机器信息 运行机器信息 import org.slf4j.Logger; import org.slf4j.LoggerFactory;import java.lang.invoke.MethodHandles;/*** 机器工具类*/ public abstract class ServerU…...

【LeetCode】71. 简化路径
1 问题 给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 / 开头),请你将其转化为更加简洁的规范路径。 在 Unix 风格的文件系统中,一个点(.)表示当前目录本身…...

操作系统【OS】进程的控制【进程的创建、终止、阻塞、唤醒】
定义和过程 对应事件 创建 允许一个进程创建另一个进程允许子进程继承父进程所拥有的资源创建进程的过程如下: 申请一个空白的 PCB,并向 PCB 中填写一些控制和管理进程的信息,比如进程的唯一标识等;为该进程分配运行时所必需的…...
 构建标记流)
写一个简单的解释器(2) 构建标记流
确定标记类型 分为几个大类: 用户符号(类型/标识符/数字/字符串…)关键字 (流程控制和定义符)括号 (这里暂时认为 [] 属于括号)分号 上述四类标记基本囊括了 vc \texttt{vc} vc 中的所有最小单元的类型,但是因为构…...
Leetcode1833. 雪糕的最大数量
Every day a Leetcode 题目来源:1833. 雪糕的最大数量 解法1:贪心 排序 本题唯一的难点在于计数排序。 计数排序详解:C算法之计数排序 为了尽可能多的买到雪糕,我们选择从价格低的雪糕开始买,统计能够买到的雪糕…...
idea 里 没有svn选项的处理办法
总结一下没有svn选项的几种情况: 情况1:IntelliJ IDEA打开带SVN信息的项目不显示SVN信息,项目右键SVN以及图标还有Changes都不显示解决方法 在VCS菜单中有个开关,叫Enabled Version Control Integration,在打开的窗口…...

基于SpringBoot的招生管理系统
基于SpringBoot的招生管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringBootMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 登录界面 管理员界面 用户界面 摘要 基于SpringBoot的招生管理系统是一款现…...

01、MySQL-------性能优化
目录 一、影响性能的相关因素存储过程: 二、sql优化1>、Mysql系统架构2>、引擎区别: 3>、索引1、什么是索引?联合主键索引理解:索引长度理解:什么是慢查询? 1)、索引理解2)…...

Flutter - APP跳转高德、百度、腾讯、谷歌地图
demo 地址: https://github.com/iotjin/jh_flutter_demo 代码不定时更新,请前往github查看最新代码 这里介绍的是不需要自己开发地图,直接通过给定的经纬度,跳转到三方地图APP调用导航的方式 一种是写的工具类,一种是通过调用三方…...
Flyway Desktop updated
Flyway Desktop updated 为比较工件序列化和反序列化添加了额外的调试日志记录。 Flyway Desktop现在将记住以前用于创建项目和匹配克隆的位置。 新的脱机许可工作流现在已在Microsoft Windows上启用。 现在,在配置目标数据库列表时,环境ID是可见的。 现…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...
