【算法练习Day25】 重新安排行程N 皇后 解数独

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 重新安排行程
- N 皇后
- 解数独
- 总结:
重新安排行程
LeetCode 332. 重新安排行程
题目描述:给你一份航线列表 tickets ,其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。
例如,行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小,排序更靠前。
假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。
示例 1:
示例1:输入:tickets = [[“MUC”,“LHR”],[“JFK”,“MUC”],[“SFO”,“SJC”],[“LHR”,“SFO”]]
输出:[“JFK”,“MUC”,“LHR”,“SFO”,“SJC”]
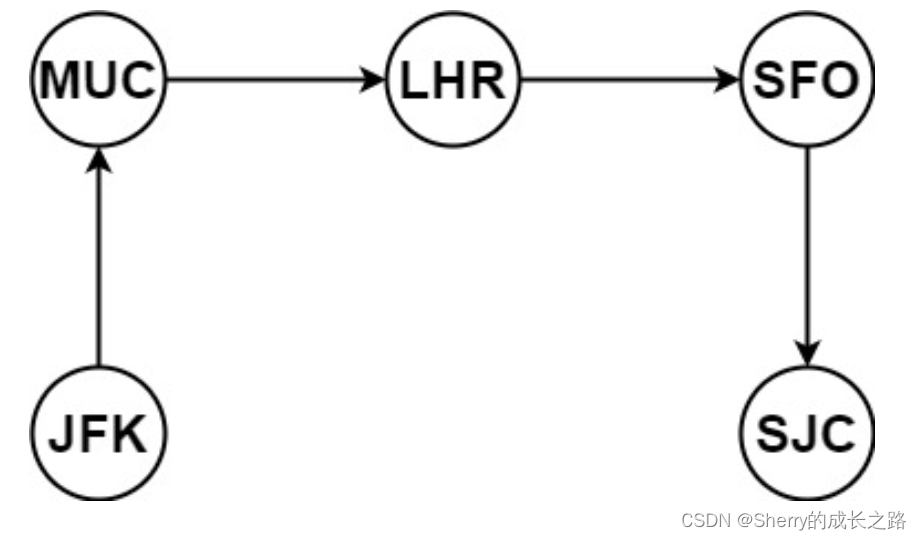
思路:
这道题目有几个难点:
一个行程中,如果航班处理不好容易变成一个圈,成为死循环
有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
使用回溯法(也可以说深搜) 的话,那么终止条件是什么呢?
搜索的过程中,如何遍历一个机场所对应的所有机场。
class Solution {
public:unordered_map<string,map<string,int>> targets;bool backtracking(int ticketNum,vector<string>&result){if(result.size()==ticketNum+1){return true;}for(pair<const string,int>& target: targets[result[result.size()-1]]){if(target.second>0){result.push_back(target.first);target.second--;if(backtracking(ticketNum,result)){return true;}result.pop_back();target.second++;}}return false;}vector<string> findItinerary(vector<vector<string>>& tickets) {targets.clear();vector<string> result;for(const vector<string>&vec:tickets){targets[vec[0]][vec[1]]++;}result.push_back("JFK");backtracking(tickets.size(),result);return result;}
};
N 皇后
LeetCode 51 N 皇后
题目描述:按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例1:输入:n = 4
输出:[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释:如下图所示,4 皇后问题存在两个不同的解法
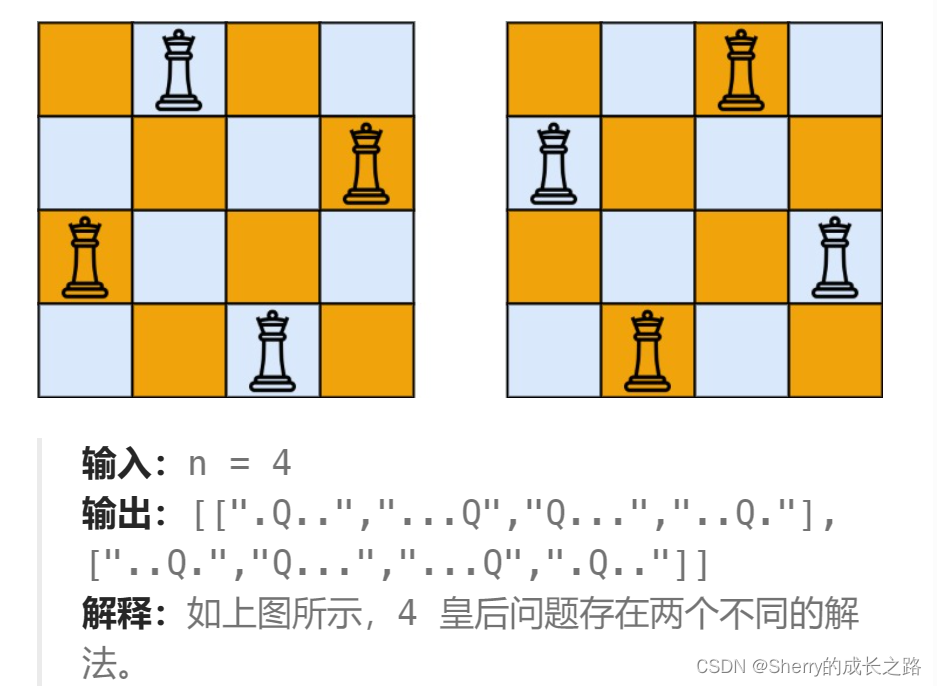
示例2:输入:n = 1
输出:[[“Q”]]
class Solution {
public:vector<vector<string>> result;void backtracking(int n,int row,vector<string>& chessboard){if(row==n){result.push_back(chessboard);return;}for(int col=0;col<n;col++){if(isValid(row,col,chessboard,n)){chessboard[row][col]='Q';backtracking(n,row+1,chessboard);chessboard[row][col]='.';}}}bool isValid(int row,int col,vector<string>&chessboard,int n){for(int i=0;i<row;i++){if(chessboard[i][col]=='Q'){return false;}}for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){if(chessboard[i][j]=='Q'){return false;}}for(int i=row-1,j=col+1;i>=0&&j>=0;i--,j++){if(chessboard[i][j]=='Q'){return false;}}return true;}vector<vector<string>> solveNQueens(int n) {result.clear();vector<string> chessboard(n,string(n,'.'));backtracking(n,0,chessboard);return result;}
};
解数独
LeetCode 37 解数独
题目描述:编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
示例:

解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

class Solution {
public:bool backtracking(vector<vector<char>>& board){for(int i=0;i<board.size();i++){for(int j=0;j<board[0].size();j++){if(board[i][j]=='.'){for(char k='1';k<='9';k++){if(isValid(i,j,k,board)){board[i][j]=k;if(backtracking(board)){return true;}board[i][j]='.';}}return false;}}}return true;}bool isValid(int row,int col,char val,vector<vector<char>>& board){for(int i=0;i<9;i++){if(board[row][i]==val){return false;}}for(int j=0;j<9;j++){if(board[j][col]==val){return false;}}int startRow=(row/3)*3;int startCol=(col/3)*3;for(int i=startRow;i<startRow+3;i++){for(int j=startCol;j<startCol+3;j++){if(board[i][j]==val){return false;}}}return true;}void solveSudoku(vector<vector<char>>& board) {backtracking(board);}
};
总结:这三道回溯题我是一题没看懂,一刷大概了解一下吧,废了,不过N皇后挺经典的,这三题还是要掌握。
总结:
今天我们完成了重新安排行程、N 皇后、解数独三道题,相关的思想需要多复习回顾。接下来,我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【算法练习Day25】 重新安排行程N 皇后 解数独
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 重新安排行程N 皇后解数独总…...

软考-访问控制技术原理与应用
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 by 2023年10月 访问控制概念 访问控制是计算机安全的一个重要组成部分,用于控制用户或程序如…...

优测云测试平台 | 有效的单元测试
一、前言 本文作者提出了一种评价单元测试用例的质量的思路,即判断用例是否达到测试的“四大目标”。掌握识别好的用例的能力,可以帮助我们高效地写出高质量的测试用例。 评判冰箱的好坏,并不需要有制造一台冰箱的能力。在开始写测试用例之…...
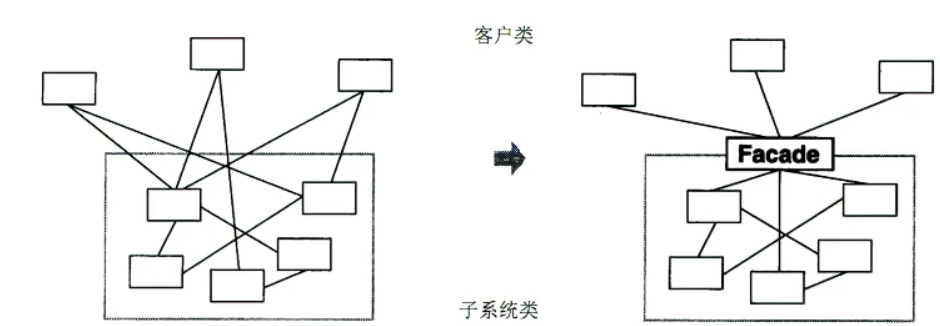
Java设计模式之外观模式
定义 又名门面模式,是一种通过为多个复杂的子系统提供一个一致的接口,而使这些子系统更加容易被访问的模式。该模式对外有一个统一接口,外部应用程序不用关心内部子系统的具体的细节,这样会大大降低应用程序的复杂度,…...

MyBatis实现延时加载的方式
MyBatis实现延时加载的方式有两种: 使用resultMap的association和collection标签配置延时加载:在查询语句中,使用association标签配置一对一关联关系,使用collection标签配置一对多关联关系。然后在查询结果映射的resultMap中配置…...
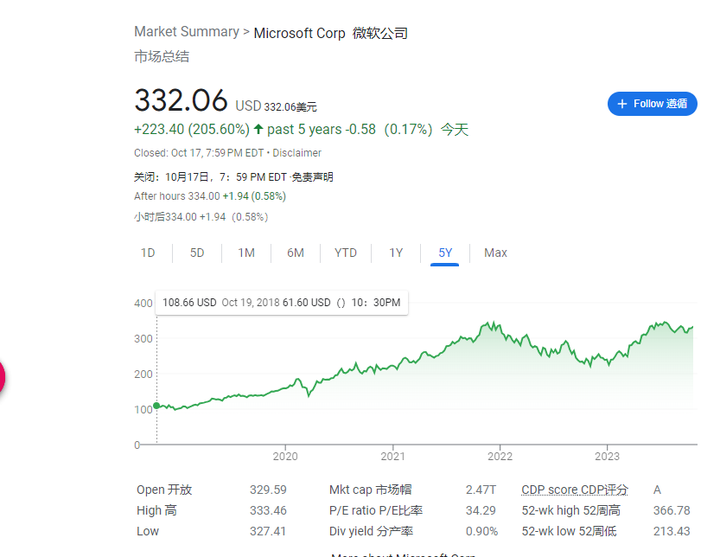
计算未来:微软眼中的人工智能
计算未来 :人工智能及其社会角色(The Future Computed. Artificial Intelligence and its role in society )这本书于2018年09月由北京大学出版社出版。 书籍的作者是:沈向洋(微软全球执行副总裁),(美&…...

字号和磅的对应关系
字号「八号」对应磅值5 字号「七号」对应磅值5.5 字号「小六」对应磅值6.5 字号「六号」对应磅值7.5 字号「小五」对应磅值9 字号「五号」对应磅值10.5 字号「小四」对应磅值12 字号「四号」对应磅值14 字号「小三」对应磅值15 字号「三号」对应磅值16 字号「小二」对应磅值18 …...
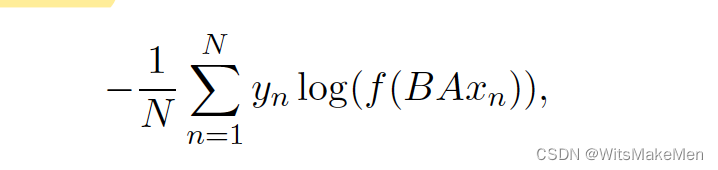
Bag of Tricks for Efficient Text Classification(FastText)
主要的有点就是快,用途就是用于文本分类,模型结构如上,主要是通过embedding将文本转换成向量,然后进行mean-pooling,然后输入到hidden隐向量中,通过softmax输出多分类,损失函数是对数似然损失函…...
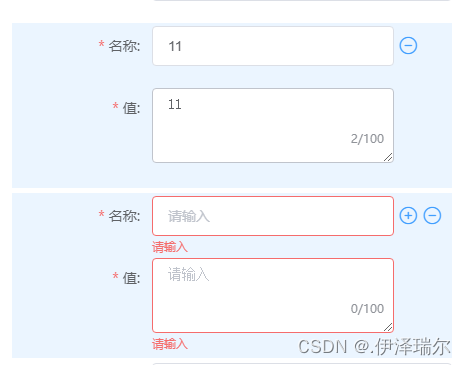
vue elementUI form组件动态添加el-form-item并且动态添加rules必填项校验方法
vue elementUI form组件动态添加el-form-item并且动态添加rules必填项校验方法 先看一下效果图(想在表单里动态的增删 form-item,然后添加rules,校验其必填项; ): html部分 <div v-for"(item, index) in …...
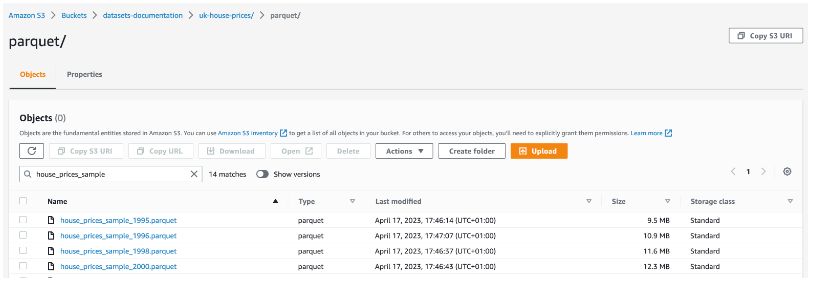
使用 ClickHouse 深入了解 Apache Parquet (一)
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 自2013年作为Hadoop的列存储发布以来,Parquet几乎已经成为一种无处不在的文件交换格式,它提供了高效的存储和检索。这种采纳使其成为更近期的…...

【每周一测】Java阶段二第四周学习
目录 1、request中的getParameter(String name)方法的功能是 2、request中的getParameter(String name)方法的功能是 3、spring创建bean对象没有以下哪个方式 4、spring依赖注入中没有以下哪个方式 5、RequestParam、RequestBody、PathVariable的应用场景及区别 6、Cooki…...

系统设计 - 我们如何通俗的理解那些技术的运行原理 - 第四部分:微服务架构
本心、输入输出、结果 文章目录 系统设计 - 我们如何通俗的理解那些技术的运行原理 - 第四部分:微服务架构前言典型的微服务架构是什么样的微服务的优势 微服务最佳实践在开发微服务时,我们需要遵循以下最佳实践: 微服务通常使用什么技术堆栈…...

顺序表ArrayList
作者简介: zoro-1,目前大二,正在学习Java,数据结构等 作者主页: zoro-1的主页 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖💖 顺序表 概念Arraylist构造方法相关方法遍历操作 自…...

python软件安装技巧
安装软件时候加上源地址去安装,快速稳 pip install openni -ihttps://pypi.tuna.tsinghua.edu.cn/simple...
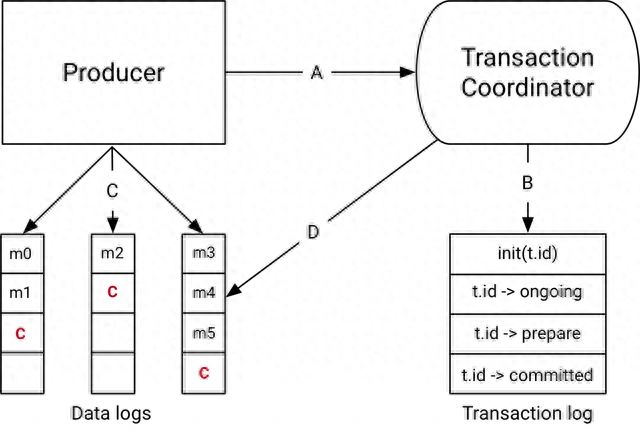
解析Apache Kafka中的事务机制
这篇博客文章并不是关于使用事务细节的教程,我们也不会深入讨论设计细节。相反,我们将在适当的地方链接到JavaDocs或设计文档,以供希望深入研究的读者使用。 为什么交易? 我们在Kafka中设计的事务主要用于那些显示“读-进程-写”模式的应用…...

Vue虚拟节点和渲染函数
1.虚拟节点 虚拟节点(dom)本质上就是一个普通的JS对象,用于描述视图的界面结构 2.渲染函数render():接收一个 createElement()函数创建的VNode Vue.component("board", {render: function(createElement) {return cr…...
后台交互-首页->与后台数据进行交互,wsx的使用
与后台数据进行交互wsx的使用 1.与后台数据进行交互 // index.js // 获取应用实例 const app getApp() const apirequire("../../config/app.js") const utilrequire("../../utils/util.js") Page({data: {imgSrcs:[{"img": "https://cd…...

【微服务保护】Sentinel 流控规则 —— 深入探索 Sentinel 的流控模式、流控效果以及对热点参数进行限流
文章目录 前言一、快速掌握 Sentinel 的使用1.1 什么是簇点链路1.2 Sentinel 的简单使用示例 二、Sentinel 流控模式2.1 直接模式2.2 关联模式2.3 链路模式 三、流控效果3.1 快速失败3.2 预热模式3.3 排队等待 四、对热点参数的流控4.1 热点规则4.2 热点规则演示 前言 微服务架…...
ZXing.Net 的Core平台生成二维码
一、引用 二、代码 帮助类 /// <summary>/// ZXing.NET 二维码帮助类/// </summary>public class ZXingHelper{/// <summary>/// 站点二维码的目录/// </summary>private static string QRCodeDirectory "QRCode";/// <summary>/// 使…...

【C++】假设给类分配的是栈的空间,那么计算机是如何访问栈中不同位置的对象的数据的呢?
2023年10月22日,周日上午 当在栈上创建一个对象时,计算机会为该对象分配一块连续的内存空间。该内存空间的位置在栈帧中,栈帧是用来存储函数调用信息和局部变量的一块内存区域。 栈帧中包含一个指针,称为栈指针(stack…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
