第十二届蓝桥杯模拟赛第三期
A填空题
问题描述
请问在 1 到 2020 中,有多少个数与 2020 互质,即有多少个数与 2020 的最大公约数为 1。
参考答案
800
public class Main {public static void main(String[] args) {int ans=0;for(int i=1;i<=2020;i++) {if(gcd(2020,i)==1) {ans++;}}System.out.println(ans);}public static int gcd(int a,int b) {if(b==0) {return a;}return gcd(b,a%b);}
}B填空题
问题描述
ASCII 码将每个字符对应到一个数值(编码),用于信息的表示和传输。在 ASCII 码中,英文字母是按从小到大的顺序依次编码的,例如:字母 A 编码是 65, 字母 B 编码是 66,字母 C 编码是 67,请问字母 Q 编码是多少?
参考答案
81
public class Main {public static void main(String[] args) {System.out.println((int)'Q');}
}C填空题
问题描述
有一棵二叉树,一个由2021个结点,其中有1000个结点有两个子结点,其他的结点有一个或者0个子结点。
请问,这棵二叉树有多少个叶结点?
参考答案
1001
//设叶子节点个数为n0,度为1的节点个数为n1,度为2的节点个数为n2,必有 n0+n1+n2 = n
//对于二叉树有:n0 = n2+1
D填空题
问题描述
对于整数 v 和 p,定义 Pierce 序列为:
a[1] = v
a[i] = p % a[i-1]
例如,当 v = 8, p = 21 时,对应的 Pierce 序列为
a[1] = 8
a[2] = 5
a[3] = 1
再往后计算,值变为 0,不在我们考虑的范围内。因此当 v = 8, p = 21 时, Pierce 序列的长度为 3。
当 p 一定时,对于不同的 v 值,Pierce 序列的长度可能不同。当 p = 8 时,若 1<=v<p,最长的 Pierce 序列出现在 v=13时,为(13, 8, 5, 1),长度为 4。
当 p = 2021 时,最长的 Pierce 序列出现在 v=1160 时,请问这个序列有多长?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
参考答案
12
public class Main {public static void main(String[] args) {int ans=0;int v=1160;int p=2021;int[] a=new int[100];a[0]=v;for(int i=1;;i++) {if(p%a[i-1]!=0) {a[i]=p%a[i-1];}else{break;}}for(int i=0;i<100;i++) {if(a[i]!=0) {ans++;}else {break;}}System.out.println(ans);}
}E填空题
问题描述
在 Excel 中,第 1 列到第 26 列的列名依次为 A 到 Z,从第 27 列开始,列名有两个字母组成,第 27 列到第 702 列的列名依次为 AA 到 ZZ。
之后的列再用 3 个字母、4 个字母表示。
请问,第 2021 列的列名是什么?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
参考答案
BYS
public class Main {public static void main(String[] args) {String str="";int n=2021;while(n>0) {n--;str=(char)(n%26+'A')+str;n=n/26;}System.out.println(str);}
}
F编程题
G编程题
H编程题
I编程题
J编程题
相关文章:

第十二届蓝桥杯模拟赛第三期
A填空题 问题描述 请问在 1 到 2020 中,有多少个数与 2020 互质,即有多少个数与 2020 的最大公约数为 1。 参考答案 800 public class Main {public static void main(String[] args) {int ans0;for(int i1;i<2020;i) {if(gcd(2020,i)1) {ans;}}…...

2023年浙大MEM考前80天上岸经验分享
时间过得真快,转眼间已经是十月份了。回想起去年这个时候,我还在为考研而感到焦虑不安。然而,如今我已经在浙大MEM项目学习了一个多月的时间了。在这一个月的学习过程中,我不仅学到了许多专业知识,还结识了很多志同道合…...

增加并行度后,发现Flink窗口不会计算的问题。
文章目录 前言一、现象二、结论三、解决 前言 窗口没有关闭计算的问题,一直困扰了很久,经过多次验证,确定了问题的根源。 一、现象 Flink使用了window,同时使用了watermark ,并且还设置了较高的并行度。生产是设置了…...

使用 JMeter 和 Docker 进行服务存根
用于性能测试的服务存根:简介 随着测试项目的复杂性不断增加,越来越多的被测系统的测试流程受到依赖系统的影响。当我说“依赖系统”时,我指的是: 不受当前开发影响的遗留系统 属于另一个组织的第三方服务 您的组织开发的系统&am…...
《王道计算机考研——操作系统》学习笔记总目录+思维导图
本篇文章是对《王道计算机考研——操作系统》所有知识点的笔记总结归档和计算机网络的思维导图 学习视频:王道计算机考研 操作系统 408四件套【计网、计组、操作系统、数据结构】完整课堂PPT 思维导图 (求Star~):【王道考研】计…...

多模态及图像安全的探索与思考
前言 第六届中国模式识别与计算机视觉大会(The 6th Chinese Conference on Pattern Recognition and Computer Vision, PRCV 2023)已于近期在厦门成功举办。通过参加本次会议,使我有机会接触到许多来自国内外的模式识别和计算机视觉领域的研究…...

基础算法相关笔记
排序 最好情况下: 冒泡排序 最坏时间复杂度 O ( n 2 ) O(n^2) O(n2)。 插入排序 最坏时间复杂度为 O ( n 2 ) O(n^2) O(n2),最优时间复杂度为 O ( n ) O(n) O(n)。 平均情况下: 快速排序 最坏时间复杂度为 O ( n 2 ) O(n^2) O(n2)&…...
Mac电脑无法识别移动硬盘怎么办?
很多人都喜欢在Mac电脑上办公、学习,但有时我们将移动硬盘连接Mac电脑时,却会发现电脑无法识别移动硬盘。那么,Mac电脑无法识别移动硬盘怎么办呢? Mac无法识别移动硬盘的原因 导致Mac不识别移动硬盘的原因有很多,你可…...

14Maven与Tomcat面试题
1MAVEN Maven是一个基于项目对象模型(POM)的项目管理工具,它可以帮助开发者自动化构建、依赖管理、项目报告等。Maven通过一个中央信息片段能够管理项目的构建、报告和文档等步骤,同时也能够管理项目的依赖。Maven的核心概念是POM…...
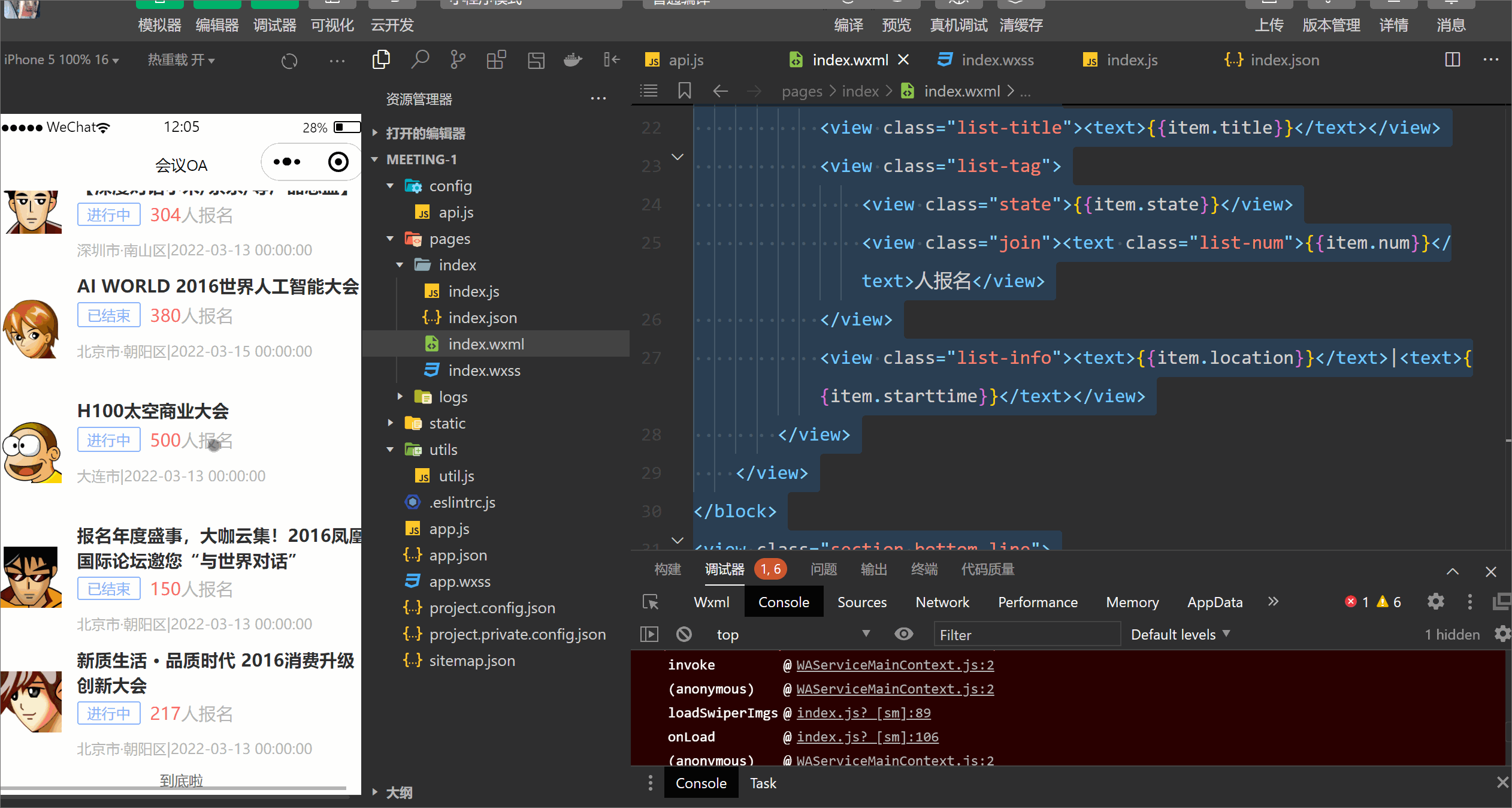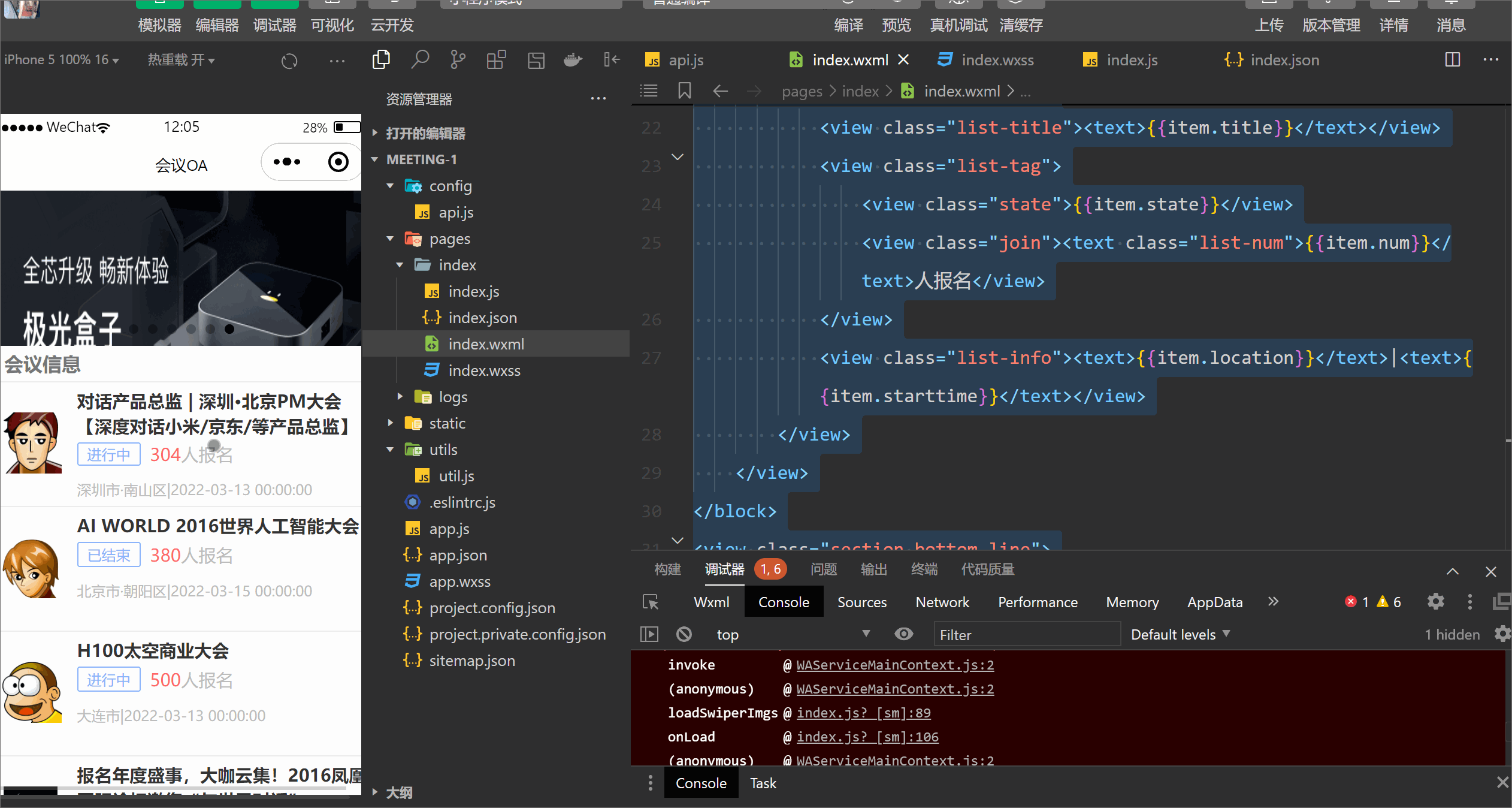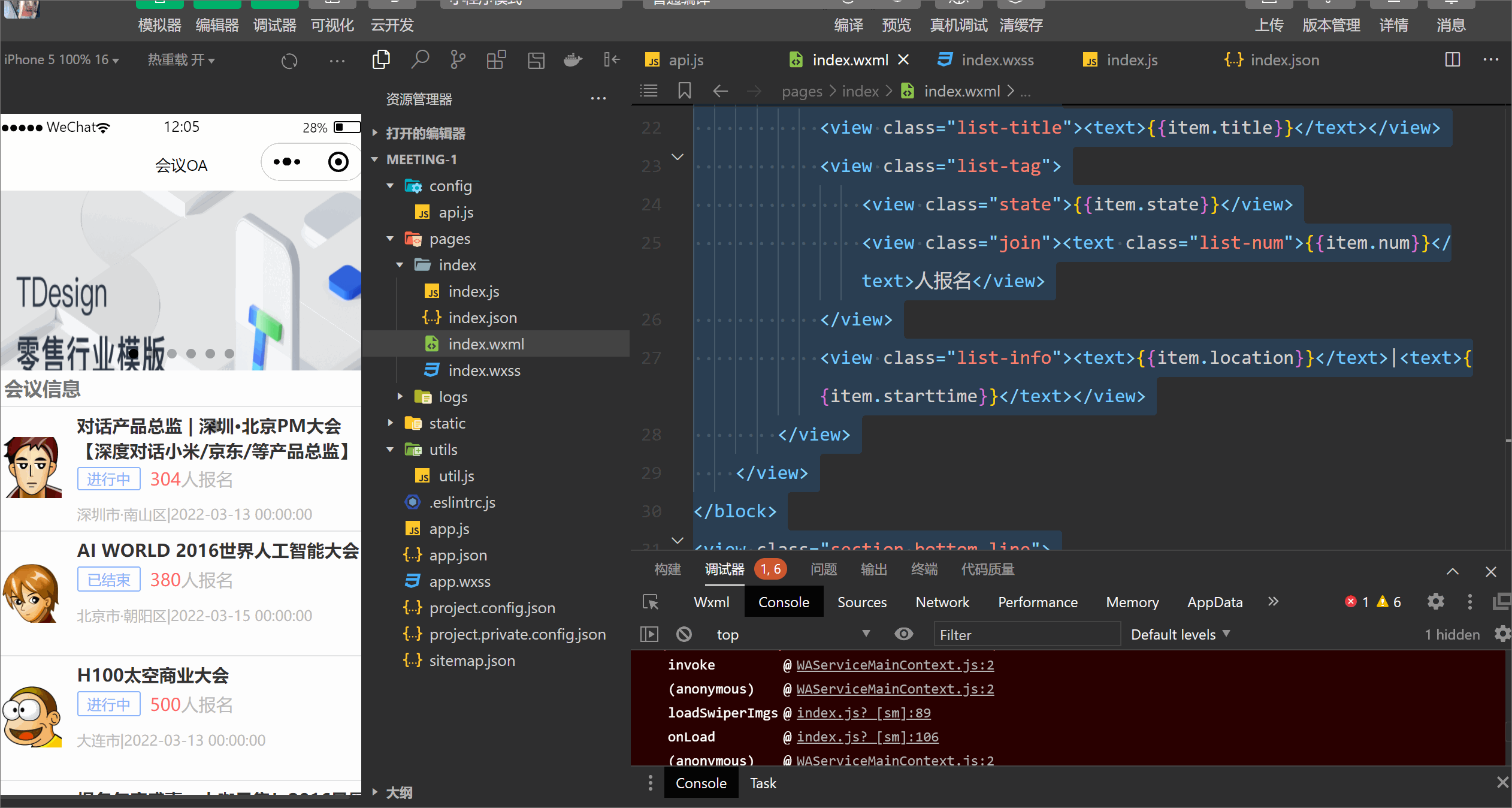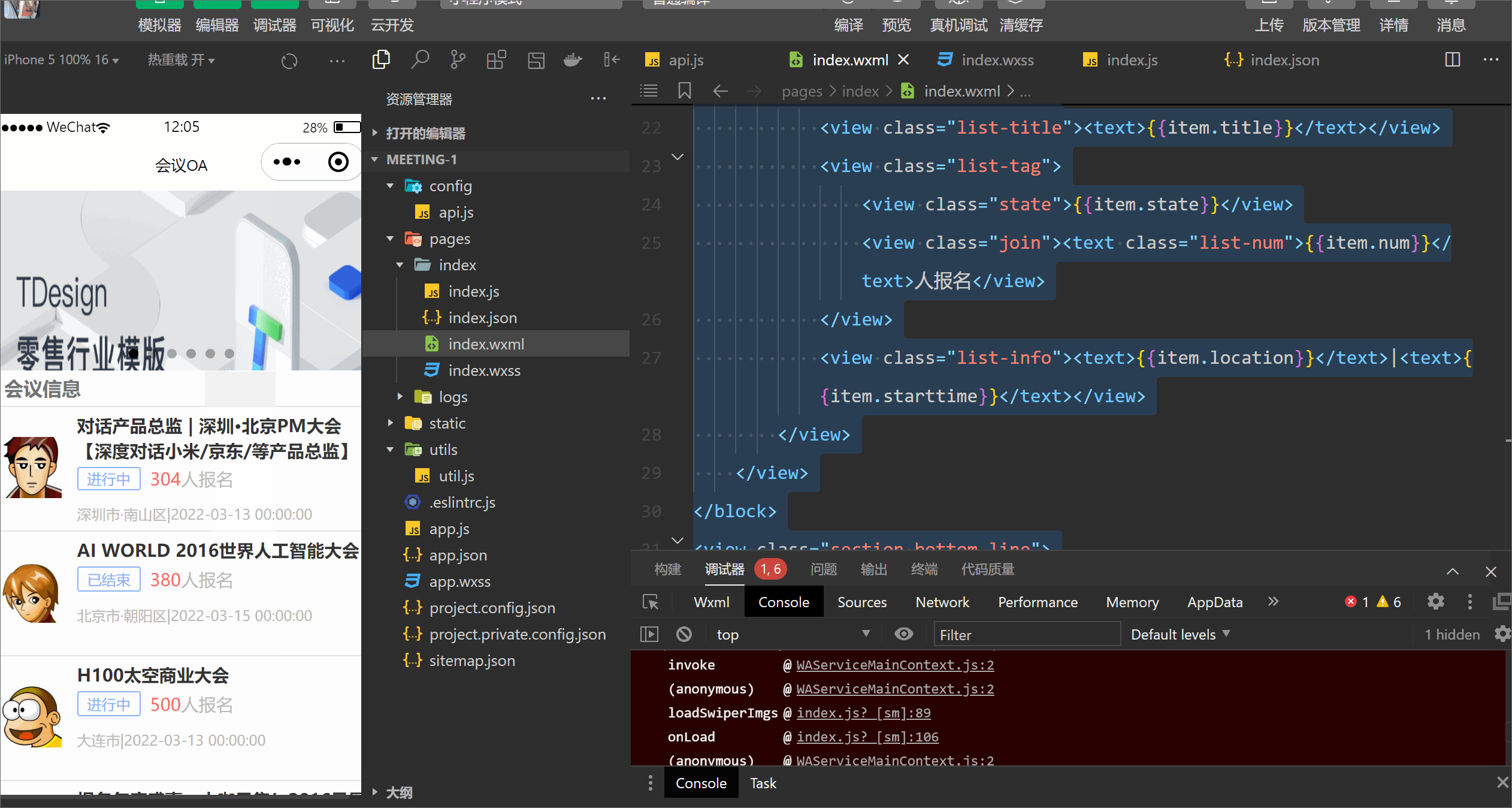
会议OA小程序【首页布局】
目录 一. Flex布局介绍 1.1 什么是Flex布局 1.2 基本概念 1.3 Flex属性 二. 会议OA首页轮播图的实现 配置 Mock工具 swiper 效果展示 三. 会议OA首页会议信息布局 index.js index.wxml index.wxss 首页整体效果展示 一. Flex布局介绍 布局的传统解决方案&#x…...

高效表达三步
一、高效表达 高效表达定主题搭架子填素材 第一: 1个核心主题,让别人秒懂你的想法 (表达要定主题) 第二: 3种经典框架,帮你快速整理表达思路 第三: 2种表达素材,让发言更具说服力…...

怎样修改ESP32的CPU主频
ESP32的主频默认设置为160mhz,但ESP32最高可以跑到240mhz, 修改方法: idf.py menuconfig --> Component config --> ESP System Settings --> CPU frequency 可以看到三个选项,80,160, 240&…...
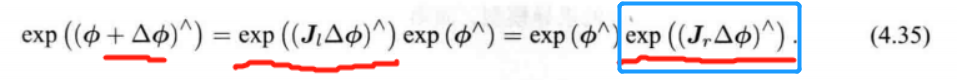
《视觉 SLAM 十四讲》V2 第 10 讲 后端优化2 简化BA 【位姿图】
文章目录 第10讲 后端210.1 滑动窗口滤波 和 优化10.1.2 滑动窗口法 10.2 位姿图10.3 实践: 位姿图优化本讲 CMakeLists.txt 10.3.1 g2o 原生位姿图 【Code】10.3.2 李代数上的位姿优化 【Code】 习题10题1 【没推完】 LaTex 第10讲 后端2 滑动窗口优化 位姿图优化…...

【斗破年番】再遭群嘲,美杜莎怀孕之事被魔改,三方联手除萧潇?
【侵权联系删除】【文/郑尔巴金】 斗破苍穹年番第67集已经更新了。和很多人一样,小郑也去看了,只是小郑万万没有想到,我满怀期待的去看这一集,这一集却能魔改成这样。魔改成什么样了呢?下面来分析下吧! 一&…...

字节面试题——计算机网络,附答案
1.TCP 三次握手和四次挥手 相关面试题: 计算机网络常见面试题总结(上) | JavaGuide(Java面试 学习指南) 为什么要三次握手?第 2 次握手传回了 ACK,为什么还要传回 SYN?为什么要四次挥手?为什么不能把服务器发送的 ACK 和 FIN…...
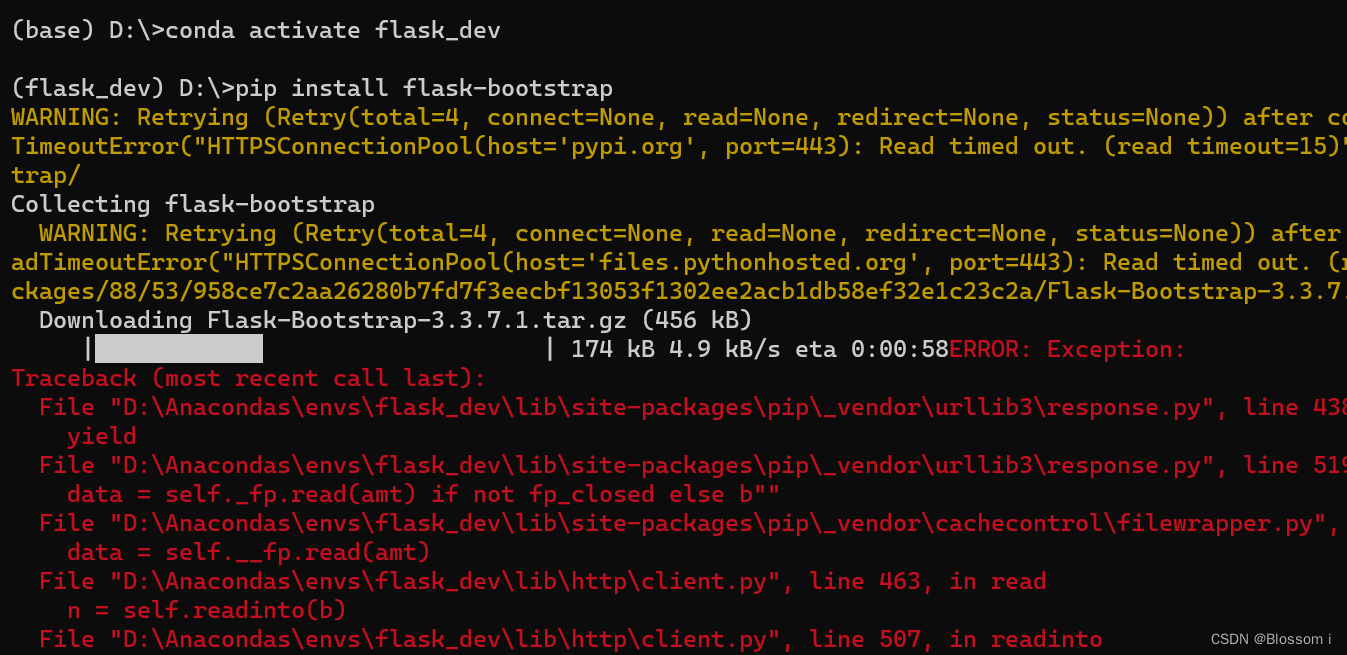
Flask Web 安装bootstrap失败pip install bootstrap
失败原因:网速太慢了 把公共wifi换成手机热点,成功:) 😃 更新:开了手机热点还是报下面的错,但是把科学上网关了,就成功了,反正就是网络问题...
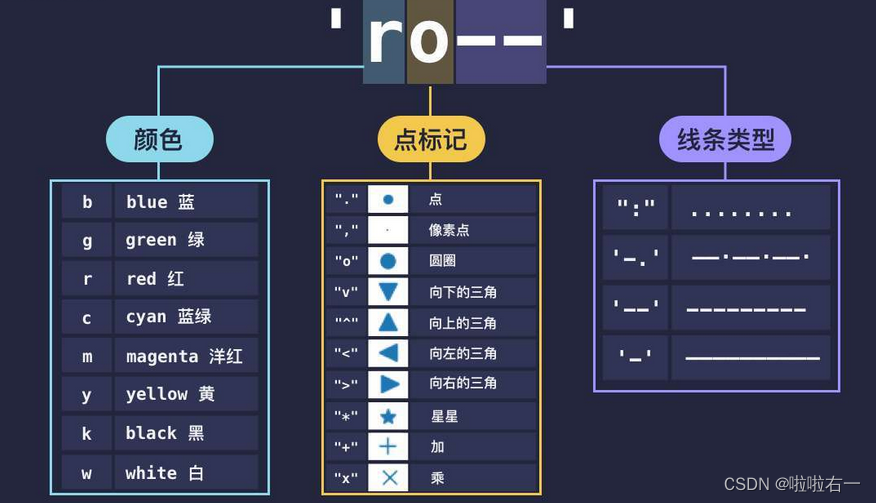
可视化 | python可视化相关库梳理(自用)| pandas | Matplotlib | Seaborn | Pyecharts | Plotly
文章目录 📚Plotly🐇堆叠柱状图🐇环形图🐇散点图🐇漏斗图🐇桑基图🐇金字塔图🐇气泡图🐇面积图⭐️快速作图工具:plotly.express🐇树形图…...
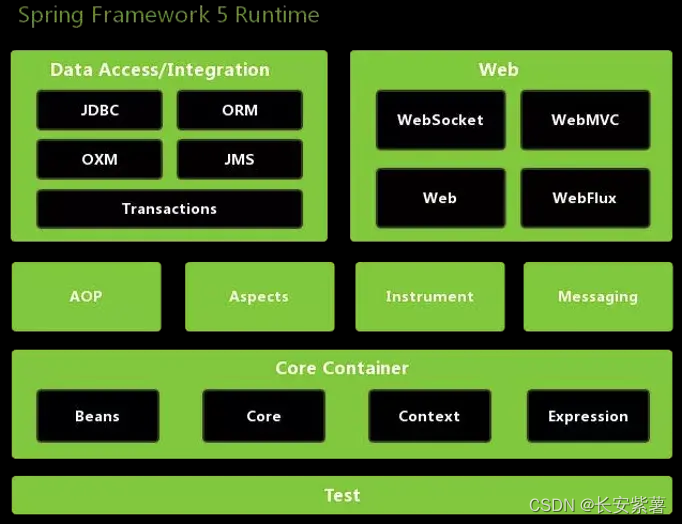
黑豹程序员-架构师学习路线图-百科:Java的第二春Spring框架
文章目录 1、 Spring的发展历史2、为什么Spring能霸屏?2.1、容器的设计2.2、通过四个策略2.3、三种方式 3、学习编程设计的典范 1、 Spring的发展历史 正当SUN公司的EJB在全球开始热炒时,正当程序员纷纷转型EJB开发时,正当程序员为跑通EJB程…...

C#获取指定软件安装路径
作用 每个电脑安装的路径不一致会导致无法动态获取指定软件的安装路径,通过注册表来获取安装路径 代码 RegistryKey registryKeyPro Registry.LocalMachine.OpenSubKey("SOFTWARE\\****"); string installDir (string)(registryKeyPro.GetValue(&quo…...

统计射击比赛成绩
题目描述 给定一个射击比赛成绩单,包含多个选手若干次射击的成绩分数,请对每个选手按其最高3个分数之和进行降序排名,输出降序排名后的选手ID序列。 条件如下 ① 一个选手可以有多个射击成绩的分数,且次序不固定。 ② 如果一个选手成绩少于3个,则认为选手的所有成绩无效…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
