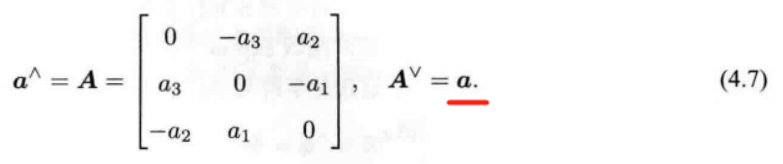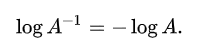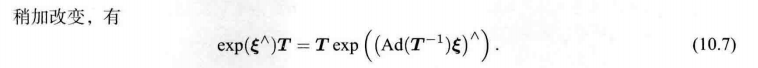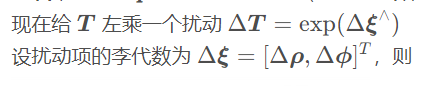《视觉 SLAM 十四讲》V2 第 10 讲 后端优化2 简化BA 【位姿图】

文章目录
- 第10讲 后端2
- 10.1 滑动窗口滤波 和 优化
- 10.1.2 滑动窗口法
- 10.2 位姿图
- 10.3 实践: 位姿图优化
- 本讲 CMakeLists.txt
- 10.3.1 g2o 原生位姿图 【Code】
- 10.3.2 李代数上的位姿优化 【Code】
- 习题10
- 题1 【没推完】
- LaTex
第10讲 后端2
滑动窗口优化
位姿图优化【简化的BA】
带IMU 紧耦合 的优化
g2o 的位姿图
第9讲 以BA为主的图优化。
BA能精确地优化每个相机位姿与特征点位置。
在大场景中,大量特征点 会严重降低计算效率,计算量越来越大 ——> 无法实时化。
改进: 简化BA 【位姿图】
10.1 滑动窗口滤波 和 优化
BA:带有相机位姿和空间点的图优化。
控制 BA 规模:仅保留 离当前时刻最近的 N 个关键帧。【滑动窗口法】
ORB-SLAM2 :
共视图(Covisibility graph) : 与现在的相机 存在共同观测的关键帧构成的图。
10.1.2 滑动窗口法



滑动窗口法 比较适合VO系统,不适合大规模建图系统。
10.2 位姿图

10.3 实践: 位姿图优化
本讲 CMakeLists.txt
cmake_minimum_required(VERSION 2.8)
project(pose_graph)set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-std=c++17 -O2")list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake_modules)# Eigen
include_directories("/usr/include/eigen3")# sophus
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})# g2o
find_package(G2O REQUIRED)
include_directories(${G2O_INCLUDE_DIRS})add_executable(pose_graph_g2o_SE3 pose_graph_g2o_SE3.cpp)
target_link_libraries(pose_graph_g2o_SE3g2o_core g2o_stuff g2o_types_slam3d ${CHOLMOD_LIBRARIES})SET(G2O_LIBS g2o_csparse_extension g2o_stuff g2o_core cxsparse)add_executable(pose_graph_g2o_lie pose_graph_g2o_lie_algebra.cpp)
target_link_libraries(pose_graph_g2o_lie${G2O_LIBS}${CHOLMOD_LIBRARIES}${Sophus_LIBRARIES})
——————————
改动1:
SE3d 和 SO3d 去掉d
改动2:
CMakeLists.txt 加这一句 使满足 C++17标准, 最新版 g2o 需要
改动3: CMakeLists.txt 添加 csparse 相关的链接库
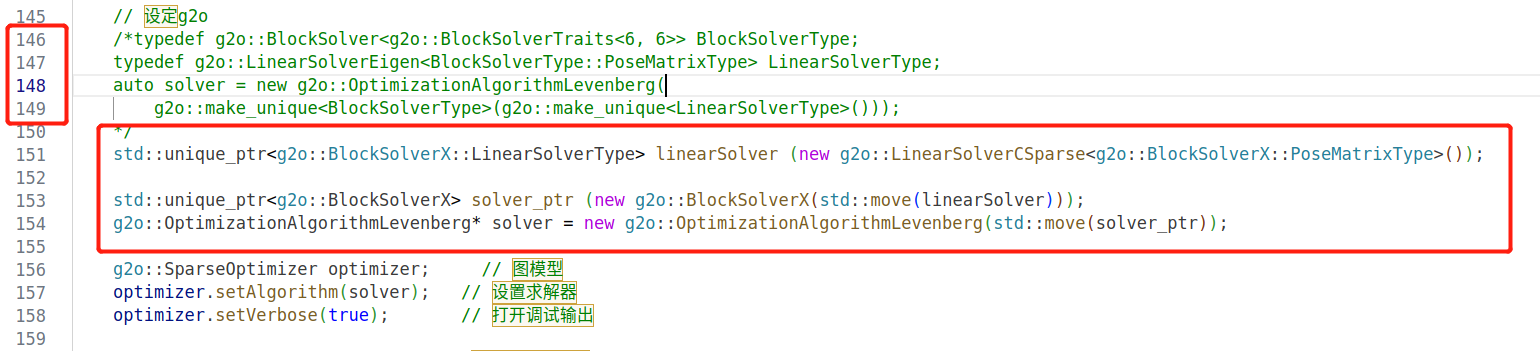
std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linearSolver (new g2o::LinearSolverEigen<g2o::BlockSolverX::PoseMatrixType>()); // 这里直接用 前面提到的Eigen 线性方程求解库 也可以std::unique_ptr<g2o::BlockSolverX> solver_ptr (new g2o::BlockSolverX(std::move(linearSolver)));g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));
10.3.1 g2o 原生位姿图 【Code】
查看待优化的位姿图。注意在文件sphere.g2o所在文件夹打开命令行窗口。
g2o_viewer sphere.g2o

mkdir build && cd build
cmake ..
make
./pose_graph_g2o_SE3 ../sphere.g2o
g2o_viewer result.g2o


pose_graph_g2o_SE3.cpp
#include <iostream>
#include <fstream>
#include <string>#include <g2o/types/slam3d/types_slam3d.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>using namespace std;/************************************************* 本程序演示如何用g2o solver进行位姿图优化* sphere.g2o是人工生成的一个Pose graph,我们来优化它。* 尽管可以直接通过load函数读取整个图,但我们还是自己来实现读取代码,以期获得更深刻的理解* 这里使用g2o/types/slam3d/中的SE3表示位姿,它实质上是四元数而非李代数.* **********************************************/int main(int argc, char **argv) {if (argc != 2) {cout << "Usage: pose_graph_g2o_SE3 sphere.g2o" << endl;return 1;}ifstream fin(argv[1]);if (!fin) {cout << "file " << argv[1] << " does not exist." << endl;return 1;}// 设定g2o/*typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 6>> BlockSolverType;typedef g2o::LinearSolverEigen<BlockSolverType::PoseMatrixType> LinearSolverType;auto solver = new g2o::OptimizationAlgorithmLevenberg(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
*/ std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linearSolver (new g2o::LinearSolverEigen<g2o::BlockSolverX::PoseMatrixType>());std::unique_ptr<g2o::BlockSolverX> solver_ptr (new g2o::BlockSolverX(std::move(linearSolver)));g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));g2o::SparseOptimizer optimizer; // 图模型optimizer.setAlgorithm(solver); // 设置求解器optimizer.setVerbose(true); // 打开调试输出int vertexCnt = 0, edgeCnt = 0; // 顶点和边的数量while (!fin.eof()) {string name;fin >> name;if (name == "VERTEX_SE3:QUAT") {// SE3 顶点g2o::VertexSE3 *v = new g2o::VertexSE3();int index = 0;fin >> index;v->setId(index);v->read(fin);optimizer.addVertex(v);vertexCnt++;if (index == 0)v->setFixed(true);} else if (name == "EDGE_SE3:QUAT") {// SE3-SE3 边g2o::EdgeSE3 *e = new g2o::EdgeSE3();int idx1, idx2; // 关联的两个顶点fin >> idx1 >> idx2;e->setId(edgeCnt++);e->setVertex(0, optimizer.vertices()[idx1]);e->setVertex(1, optimizer.vertices()[idx2]);e->read(fin);optimizer.addEdge(e);}if (!fin.good()) break;}cout << "read total " << vertexCnt << " vertices, " << edgeCnt << " edges." << endl;cout << "optimizing ..." << endl;optimizer.initializeOptimization();optimizer.optimize(30);cout << "saving optimization results ..." << endl;optimizer.save("result.g2o");return 0;
}
10.3.2 李代数上的位姿优化 【Code】
前端和后端 分开: 跟踪和建图
报错:
xixi@ubuntu:~/Downloads/slambook2-master/ch10/build$ ./pose_graph_g2o_lie ../sphere.g2o
Segmentation fault
./pose_graph_g2o_lie ../sphere.g2o
g2o_viewer result.g2o

pose_graph_g2o_lie_algebra.cpp
#include <iostream>
#include <fstream>
#include <string>
#include <Eigen/Core>#include <g2o/core/base_vertex.h>
#include <g2o/core/base_binary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>#include <sophus/se3.h>using namespace std;
using namespace Eigen;
using Sophus::SE3;
using Sophus::SO3;/************************************************* 本程序演示如何用g2o solver进行位姿图优化* sphere.g2o是人工生成的一个Pose graph,我们来优化它。* 尽管可以直接通过load函数读取整个图,但我们还是自己来实现读取代码,以期获得更深刻的理解* 本节使用李代数表达位姿图,节点和边的方式为自定义* **********************************************/typedef Matrix<double, 6, 6> Matrix6d;// 给定误差求J_R^{-1}的近似
Matrix6d JRInv(const SE3 &e) {Matrix6d J;J.block(0, 0, 3, 3) = SO3::hat(e.so3().log());J.block(0, 3, 3, 3) = SO3::hat(e.translation());J.block(3, 0, 3, 3) = Matrix3d::Zero(3, 3);J.block(3, 3, 3, 3) = SO3::hat(e.so3().log());// J = J * 0.5 + Matrix6d::Identity();J = Matrix6d::Identity(); // try Identity if you wantreturn J;
}// 李代数顶点
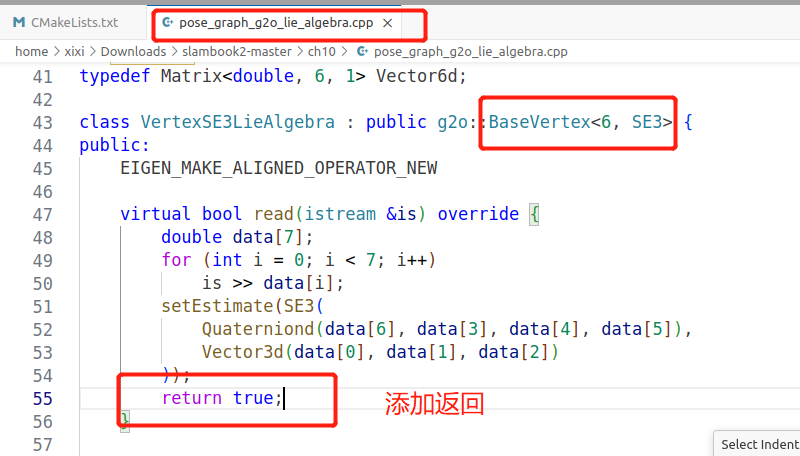
typedef Matrix<double, 6, 1> Vector6d;class VertexSE3LieAlgebra : public g2o::BaseVertex<6, SE3> {
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWvirtual bool read(istream &is) override {double data[7];for (int i = 0; i < 7; i++)is >> data[i];setEstimate(SE3(Quaterniond(data[6], data[3], data[4], data[5]),Vector3d(data[0], data[1], data[2])));return true;}virtual bool write(ostream &os) const override {os << id() << " ";Quaterniond q = _estimate.unit_quaternion();os << _estimate.translation().transpose() << " ";os << q.coeffs()[0] << " " << q.coeffs()[1] << " " << q.coeffs()[2] << " " << q.coeffs()[3] << endl;return true;}virtual void setToOriginImpl() override {_estimate = SE3();}// 左乘更新virtual void oplusImpl(const double *update) override {Vector6d upd;upd << update[0], update[1], update[2], update[3], update[4], update[5];_estimate = SE3::exp(upd) * _estimate;}
};// 两个李代数节点之边
class EdgeSE3LieAlgebra : public g2o::BaseBinaryEdge<6, SE3, VertexSE3LieAlgebra, VertexSE3LieAlgebra> {
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWvirtual bool read(istream &is) override {double data[7];for (int i = 0; i < 7; i++)is >> data[i];Quaterniond q(data[6], data[3], data[4], data[5]);q.normalize();setMeasurement(SE3(q, Vector3d(data[0], data[1], data[2])));for (int i = 0; i < information().rows() && is.good(); i++)for (int j = i; j < information().cols() && is.good(); j++) {is >> information()(i, j);if (i != j)information()(j, i) = information()(i, j);}return true;}virtual bool write(ostream &os) const override {VertexSE3LieAlgebra *v1 = static_cast<VertexSE3LieAlgebra *> (_vertices[0]);VertexSE3LieAlgebra *v2 = static_cast<VertexSE3LieAlgebra *> (_vertices[1]);os << v1->id() << " " << v2->id() << " ";SE3 m = _measurement;Eigen::Quaterniond q = m.unit_quaternion();os << m.translation().transpose() << " ";os << q.coeffs()[0] << " " << q.coeffs()[1] << " " << q.coeffs()[2] << " " << q.coeffs()[3] << " ";// information matrix for (int i = 0; i < information().rows(); i++)for (int j = i; j < information().cols(); j++) {os << information()(i, j) << " ";}os << endl;return true;}// 误差计算与书中推导一致virtual void computeError() override {SE3 v1 = (static_cast<VertexSE3LieAlgebra *> (_vertices[0]))->estimate();SE3 v2 = (static_cast<VertexSE3LieAlgebra *> (_vertices[1]))->estimate();_error = (_measurement.inverse() * v1.inverse() * v2).log();}// 雅可比计算virtual void linearizeOplus() override {SE3 v1 = (static_cast<VertexSE3LieAlgebra *> (_vertices[0]))->estimate();SE3 v2 = (static_cast<VertexSE3LieAlgebra *> (_vertices[1]))->estimate();Matrix6d J = JRInv(SE3::exp(_error));// 尝试把J近似为I?_jacobianOplusXi = -J * v2.inverse().Adj();_jacobianOplusXj = J * v2.inverse().Adj();}
};int main(int argc, char **argv) {if (argc != 2) {cout << "Usage: pose_graph_g2o_SE3_lie sphere.g2o" << endl;return 1;}ifstream fin(argv[1]);if (!fin) {cout << "file " << argv[1] << " does not exist." << endl;return 1;}// 设定g2o/*typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 6>> BlockSolverType;typedef g2o::LinearSolverEigen<BlockSolverType::PoseMatrixType> LinearSolverType;auto solver = new g2o::OptimizationAlgorithmLevenberg(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));*/std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linearSolver (new g2o::LinearSolverEigen<g2o::BlockSolverX::PoseMatrixType>());std::unique_ptr<g2o::BlockSolverX> solver_ptr (new g2o::BlockSolverX(std::move(linearSolver)));g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));g2o::SparseOptimizer optimizer; // 图模型optimizer.setAlgorithm(solver); // 设置求解器optimizer.setVerbose(true); // 打开调试输出int vertexCnt = 0, edgeCnt = 0; // 顶点和边的数量vector<VertexSE3LieAlgebra *> vectices;vector<EdgeSE3LieAlgebra *> edges;while (!fin.eof()) {string name;fin >> name;if (name == "VERTEX_SE3:QUAT") {// 顶点VertexSE3LieAlgebra *v = new VertexSE3LieAlgebra();int index = 0;fin >> index;v->setId(index);v->read(fin);optimizer.addVertex(v);vertexCnt++;vectices.push_back(v);if (index == 0)v->setFixed(true);} else if (name == "EDGE_SE3:QUAT") {// SE3-SE3 边EdgeSE3LieAlgebra *e = new EdgeSE3LieAlgebra();int idx1, idx2; // 关联的两个顶点fin >> idx1 >> idx2;e->setId(edgeCnt++);e->setVertex(0, optimizer.vertices()[idx1]);e->setVertex(1, optimizer.vertices()[idx2]);e->read(fin);optimizer.addEdge(e);edges.push_back(e);}if (!fin.good()) break;}cout << "read total " << vertexCnt << " vertices, " << edgeCnt << " edges." << endl;cout << "optimizing ..." << endl;optimizer.initializeOptimization();optimizer.optimize(30);cout << "saving optimization results ..." << endl;// 因为用了自定义顶点且没有向g2o注册,这里保存自己来实现// 伪装成 SE3 顶点和边,让 g2o_viewer 可以认出ofstream fout("result_lie.g2o");for (VertexSE3LieAlgebra *v:vectices) {fout << "VERTEX_SE3:QUAT ";v->write(fout);}for (EdgeSE3LieAlgebra *e:edges) {fout << "EDGE_SE3:QUAT ";e->write(fout);}fout.close();return 0;
}习题10

题1 【没推完】
如果将位姿图中的误差定义为 Δ ξ i j = ξ i ∘ ξ j − 1 \Delta \bm{\xi}_{ij}=\bm{\xi}_{i} \circ \bm{\xi}^{-1}_{j} Δξij=ξi∘ξj−1 ,推导按照此定义的左乘扰动雅克比矩阵。
本题中 位姿图的误差定义为 Δ ξ i j = ξ i ∘ ξ j − 1 = ln ( T i T j − 1 ) ∨ \Delta \bm{\xi}_{ij}=\bm{\xi}_{i} \circ \bm{\xi}^{-1}_{j}=\ln (\bm{T}_i\bm{T}_j^{-1})^{\vee} Δξij=ξi∘ξj−1=ln(TiTj−1)∨
- 和 P271 的定义区别在于 是第二个 求逆。这里是相对第 j j j 个位姿的坐标系进行位姿变化讨论
- T \bm{T} T 对应的李代数为 ξ \bm{\xi} ξ
对应的李群写法为: T j i = T i T j − 1 \bm{T}_{ji}=\bm{T}_i\bm{T}_j^{-1} Tji=TiTj−1
构建误差 e i j \bm{e}_{ij} eij
- 这样构建的误差理想下是0,因为 ln( I ) = 0 \bm{I})=\bm{0} I)=0。怎么感觉应该是下面这样的🤔
e i j = ln ( T j i − 1 T i T j − 1 ) ∨ \bm{e}_{ij}=\ln (\bm{T}_{ji}^{-1}\bm{T}_i\bm{T}_j^{-1})^{\vee} eij=ln(Tji−1TiTj−1)∨
其中
T j i = T i T j − 1 \bm{T}_{ji}=\bm{T}_i\bm{T}_j^{-1} Tji=TiTj−1
T j i − 1 T j i = T j i − 1 T i T j − 1 \bm{T}_{ji}^{-1}\bm{T}_{ji}=\bm{T}_{ji}^{-1}\bm{T}_i\bm{T}_j^{-1} Tji−1Tji=Tji−1TiTj−1
I = T j i − 1 T i T j − 1 \bm{I}=\bm{T}_{ji}^{-1}\bm{T}_i\bm{T}_j^{-1} I=Tji−1TiTj−1
给 ξ i \bm{\xi}_i ξi 和 ξ j \bm{\xi}_j ξj 各一个左扰动
e ^ i j = ln ( T j i − 1 exp ( Δ ξ i ∧ ) T i ( exp ( Δ ξ j ∧ ) T j ) − 1 ) ∨ = ln ( T j i − 1 exp ( Δ ξ i ∧ ) T i T j − 1 ( exp ( Δ ξ j ∧ ) − 1 ) ∨ 由式 ( 10.7 ) = ln ( T j i − 1 T i exp ( ( A d ( T i − 1 ) Δ ξ i ) ∧ ) exp ( ( − A d ( T j − 1 ) Δ ξ j ) ∧ ) T j − 1 ) ∨ = l n ( T j i − 1 T i T j − 1 exp ( ( A d ( T i − 1 ) Δ ξ i ) ∧ ) exp ( ( − A d ( T j − 1 ) Δ ξ j ) ∧ ) ) ∨ = l n ( exp ( e i j ) exp ( ( A d ( T i − 1 ) Δ ξ i ) ∧ ) exp ( ( − A d ( T j − 1 ) Δ ξ j ) ∧ ) ) ∨ \begin{align*}\bm{\hat{e}}_{ij} &=\ln (\bm{T}_{ji}^{-1}\exp(\Delta \bm{\xi}_i^{\land})\bm{T}_i(\exp(\Delta \bm{\xi}_j^{\land})\bm{T}_j)^{-1})^{\vee} \\ &= \ln (\bm{T}_{ji}^{-1}\exp(\Delta \bm{\xi}_i^{\land})\bm{T}_i\bm{T}_j^{-1}(\exp(\Delta \bm{\xi}_j^{\land})^{-1})^{\vee} \\ & 由 式 (10.7) \\ &= \ln (\bm{T}_{ji}^{-1}\bm{T}_i\exp((\mathrm{Ad}(\bm{T}_i^{-1})\Delta \bm{\xi}_i)^{\land})\exp((\mathrm{-Ad}(\bm{T}_j^{-1})\Delta \bm{\xi}_j)^{\land})\bm{T}_j^{-1})^{\vee} \\ &= \mathrm{ln}(\bm{T}_{ji}^{-1}\bm{T}_i\bm{T}_j^{-1}\exp((\mathrm{Ad}(\bm{T}_i^{-1})\Delta \bm{\xi}_i)^{\land})\exp((\mathrm{-Ad}(\bm{T}_j^{-1})\Delta \bm{\xi}_j)^{\land}))^{\vee} \\ &= \mathrm{ln}(\exp(\bm{e}_{ij})\exp((\mathrm{Ad}(\bm{T}_i^{-1})\Delta \bm{\xi}_i)^{\land})\exp((\mathrm{-Ad}(\bm{T}_j^{-1})\Delta \bm{\xi}_j)^{\land}))^{\vee} \\ \end{align*} e^ij=ln(Tji−1exp(Δξi∧)Ti(exp(Δξj∧)Tj)−1)∨=ln(Tji−1exp(Δξi∧)TiTj−1(exp(Δξj∧)−1)∨由式(10.7)=ln(Tji−1Tiexp((Ad(Ti−1)Δξi)∧)exp((−Ad(Tj−1)Δξj)∧)Tj−1)∨=ln(Tji−1TiTj−1exp((Ad(Ti−1)Δξi)∧)exp((−Ad(Tj−1)Δξj)∧))∨=ln(exp(eij)exp((Ad(Ti−1)Δξi)∧)exp((−Ad(Tj−1)Δξj)∧))∨
由公式:
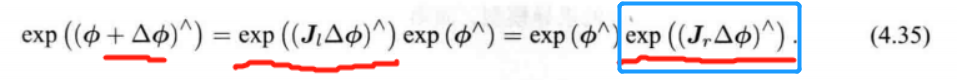
对于 T i \bm{T}_i Ti
l n ( exp ( e i j ) exp ( ( A d ( T i − 1 ) Δ ξ i ) ∧ ) exp ( ( − A d ( T j − 1 ) Δ ξ j ) ∧ ) ) ∨ ≈ \mathrm{ln}(\exp(\bm{e}_{ij})\exp((\mathrm{Ad}(\bm{T}_i^{-1})\Delta \bm{\xi}_i)^{\land})\exp((\mathrm{-Ad}(\bm{T}_j^{-1})\Delta \bm{\xi}_j)^{\land}))^{\vee} \approx ln(exp(eij)exp((Ad(Ti−1)Δξi)∧)exp((−Ad(Tj−1)Δξj)∧))∨≈
LaTex
$\circ$
∘ \circ ∘
相关文章:
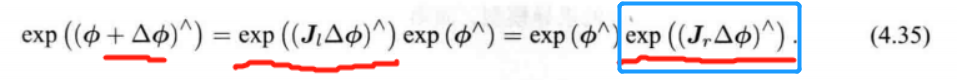
《视觉 SLAM 十四讲》V2 第 10 讲 后端优化2 简化BA 【位姿图】
文章目录 第10讲 后端210.1 滑动窗口滤波 和 优化10.1.2 滑动窗口法 10.2 位姿图10.3 实践: 位姿图优化本讲 CMakeLists.txt 10.3.1 g2o 原生位姿图 【Code】10.3.2 李代数上的位姿优化 【Code】 习题10题1 【没推完】 LaTex 第10讲 后端2 滑动窗口优化 位姿图优化…...

【斗破年番】再遭群嘲,美杜莎怀孕之事被魔改,三方联手除萧潇?
【侵权联系删除】【文/郑尔巴金】 斗破苍穹年番第67集已经更新了。和很多人一样,小郑也去看了,只是小郑万万没有想到,我满怀期待的去看这一集,这一集却能魔改成这样。魔改成什么样了呢?下面来分析下吧! 一&…...

字节面试题——计算机网络,附答案
1.TCP 三次握手和四次挥手 相关面试题: 计算机网络常见面试题总结(上) | JavaGuide(Java面试 学习指南) 为什么要三次握手?第 2 次握手传回了 ACK,为什么还要传回 SYN?为什么要四次挥手?为什么不能把服务器发送的 ACK 和 FIN…...
Flask Web 安装bootstrap失败pip install bootstrap
失败原因:网速太慢了 把公共wifi换成手机热点,成功:) 😃 更新:开了手机热点还是报下面的错,但是把科学上网关了,就成功了,反正就是网络问题...
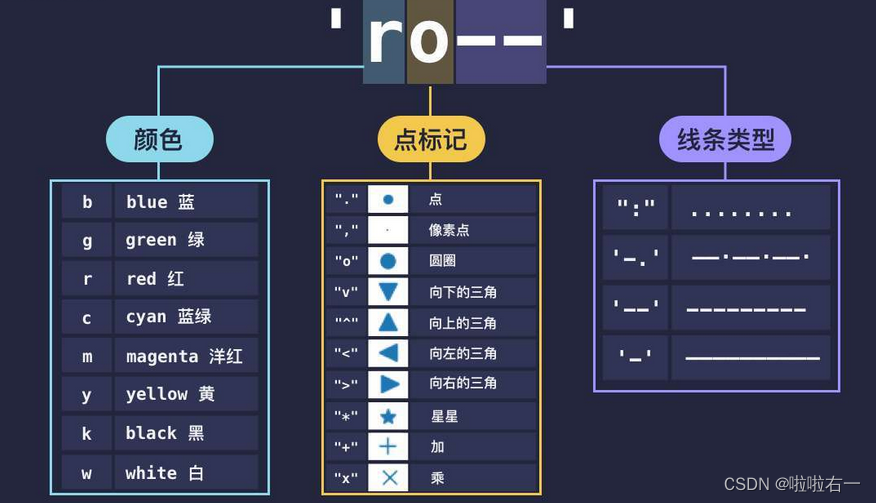
可视化 | python可视化相关库梳理(自用)| pandas | Matplotlib | Seaborn | Pyecharts | Plotly
文章目录 📚Plotly🐇堆叠柱状图🐇环形图🐇散点图🐇漏斗图🐇桑基图🐇金字塔图🐇气泡图🐇面积图⭐️快速作图工具:plotly.express🐇树形图…...
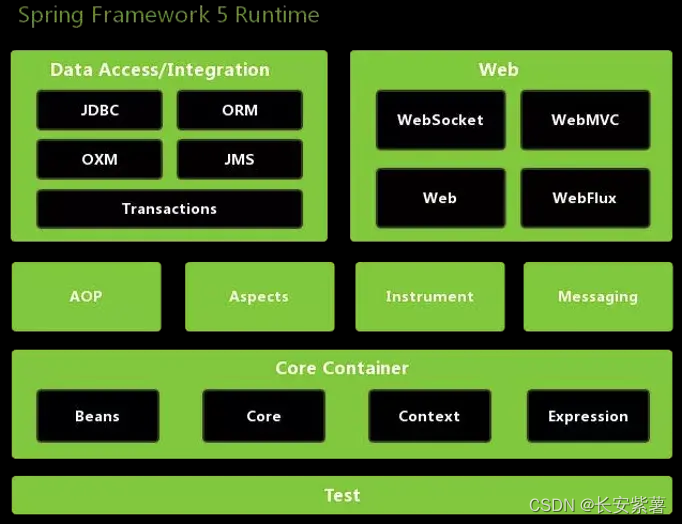
黑豹程序员-架构师学习路线图-百科:Java的第二春Spring框架
文章目录 1、 Spring的发展历史2、为什么Spring能霸屏?2.1、容器的设计2.2、通过四个策略2.3、三种方式 3、学习编程设计的典范 1、 Spring的发展历史 正当SUN公司的EJB在全球开始热炒时,正当程序员纷纷转型EJB开发时,正当程序员为跑通EJB程…...

C#获取指定软件安装路径
作用 每个电脑安装的路径不一致会导致无法动态获取指定软件的安装路径,通过注册表来获取安装路径 代码 RegistryKey registryKeyPro Registry.LocalMachine.OpenSubKey("SOFTWARE\\****"); string installDir (string)(registryKeyPro.GetValue(&quo…...

统计射击比赛成绩
题目描述 给定一个射击比赛成绩单,包含多个选手若干次射击的成绩分数,请对每个选手按其最高3个分数之和进行降序排名,输出降序排名后的选手ID序列。 条件如下 ① 一个选手可以有多个射击成绩的分数,且次序不固定。 ② 如果一个选手成绩少于3个,则认为选手的所有成绩无效…...

flink的TwoPhaseCommitSinkFunction怎么做才能提供精准一次保证
背景 TwoPhaseCommitSinkFunction是flink中基于二阶段事务提交和检查点机制配合使用实现的精准一次的输出数据汇,但是想要实现精准一次的输出,实际使用中需要注意几个方面,否则不仅仅达不到精准一次输出,反而可能导致数据丢失&am…...
1.8 基础命令CMake-set() unset())
CMake系列讲解(入门篇)1.8 基础命令CMake-set() unset()
基础命令set() unset() 〓〓〓〓〓〓〓〓踏实学CMake总目录〓〓〓〓〓〓〓〓〓〓 8. set() unset() 在CMake中,set用于设置变量的值。这个变量可以为普通变量、Cache或者是环境变量。 如果提供了一个或多个 <value> 参数,则将 <variable> 设…...

【C++ 学习 ㉙】- 详解 C++11 的 constexpr 和 decltype 关键字
目录 一、constexpr 关键字 1.1 - constexpr 修饰普通变量 1.2 - constexpr 修饰函数 1.3 - constexpr 修饰类的构造函数 1.4 - constexpr 和 const 的区别 二、decltype 关键字 2.1 - 推导规则 2.2 - 实际应用 一、constexpr 关键字 constexpr 是 C11 新引入的关键字…...

js获取视频编码
一.背景 有些浏览器不支持某些视频的编码方式导致播放出现问题,这个时候要限制视频上传 二.插件 https://unpkg.com/mediainfo.js0.1.4/dist/mediainfo.min.js 三.完整html代码 <!DOCTYPE html> <html lang"en"> <head><meta ch…...

560. 和为 K 的子数组 --力扣 --JAVA
题目 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 子数组是数组中元素的连续非空序列。 解题思路 数组项累加可以使用双层循环进行遍历;子数组的长度是不确定的,也可能存在1 1 2和1 1 - 1…...

【趣味随笔】农业机器人的种类与发展前景
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

使用CountdownLatch和线程池批量处理http请求,并处理响应数据
背景和问题 背景:最近项目的一个接口数据,需要去请求其他多个服务器的数据,然后统一返回; 问题点:如果遍历所有的服务器地址,然后串行请求就会出现请求时间过长,加入需要请求十个服务器&…...

记录--怎么写一个可以鼠标控制旋转的div?
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 说在前面 鼠标控制元素旋转在现在也是一个很常见的功能,让我们从实现div元素的旋转控制开始来了解元素旋转的具体原理和实现方法吧。 效果展示 体验地址 code.juejin.cn/pen/7290719… 实现…...

JVM第十八讲:调试排错 - Java 问题排查之工具单
调试排错 - Java 问题排查之工具单 程序员想要有更好的发展,排查问题的能力一定得加强。举个例子:cpu100% 怎么排查,线上接口逐渐变慢了该怎么排查?慢查询该如何治理?你的思路是啥?本文是JVM第十八讲&#…...
)
JAVA基础-正则表达式(12)
目录 Java 正则表达式正则表达式实例正则表达式语法 Matcher 类的方法索引方法查找方法替换方法start 和 end 方法 Java 正则表达式 正则表达式定义了字符串的模式。 正则表达式可以用来搜索、编辑或处理文本。 正则表达式并不仅限于某一种语言,但是在每种语言中有细…...

[论文笔记]GPT-1
引言 今天带来论文Improving Language Understanding by Generative Pre-Training的笔记,它的中文题目为:通过生成式预训练改进语言理解。其实就是GPT的论文。 自然语言理解可以应用于大量NLP任务上,比如文本蕴含、问答、语义相似和文档分类。虽然无标签文本语料是丰富的,…...
)
【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割1(综述篇)
在上一个关于3D 目标的任务,是基于普通CNN网络的3D分类任务。在这个任务中,分类数据采用的是CT结节的LIDC-IDRI数据集,其中对结节的良恶性、毛刺、分叶征等等特征进行了各自的等级分类。感兴趣的可以直接点击下方的链接,直达学习&…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...