跟着NatureMetabolism学作图:R语言ggplot2转录组差异表达火山图
论文
Independent phenotypic plasticity axes define distinct obesity sub-types
https://www.nature.com/articles/s42255-022-00629-2#Sec15
s42255-022-00629-2.pdf
论文中没有公开代码,但是所有作图数据都公开了,我们可以试着用论文中提供的数据模仿论文中的图
今天的推文重复一下论文中的Fig3b 差异表达火山图,之前也有推文介绍过火山图,今天的推文主要学习的一个知识点是利用latex2exp这个R包添加文本,包括
上下标
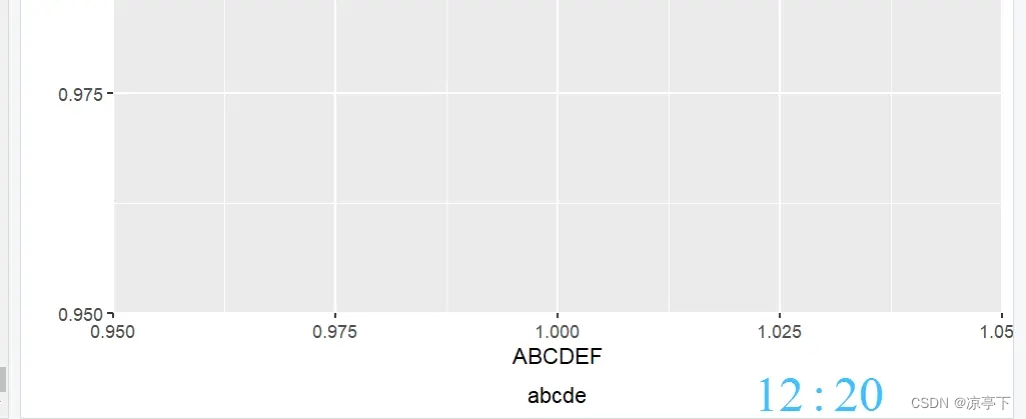
换行 换行的基本写法
ggplot()+geom_point(aes(x=1,y=1))+labs(x=TeX(r"(\overset${ABCDEF}{abcde}$)"))
火山图的部分示例数据
读取数据
library(readr)
df<-read_tsv("data/20220921/fig3b.txt")
head(df)
colnames(df)
添加差异表达的分组
df %>% mutate(change=case_when(log2FoldChange > 1 & pvalue < 0.05 ~ "Up",log2FoldChange < -1 & pvalue < 0.05 ~ "Down",TRUE ~ "Not Sig")) -> new.dftable(new.df$change)
new.df %>% filter(-log10(pvalue)>8) -> new.text.label
这里没有找到论文中差异表达的标准,这里是我随便写的
作图代码
library(ggplot2)
library(ggrepel)
library(latex2exp)
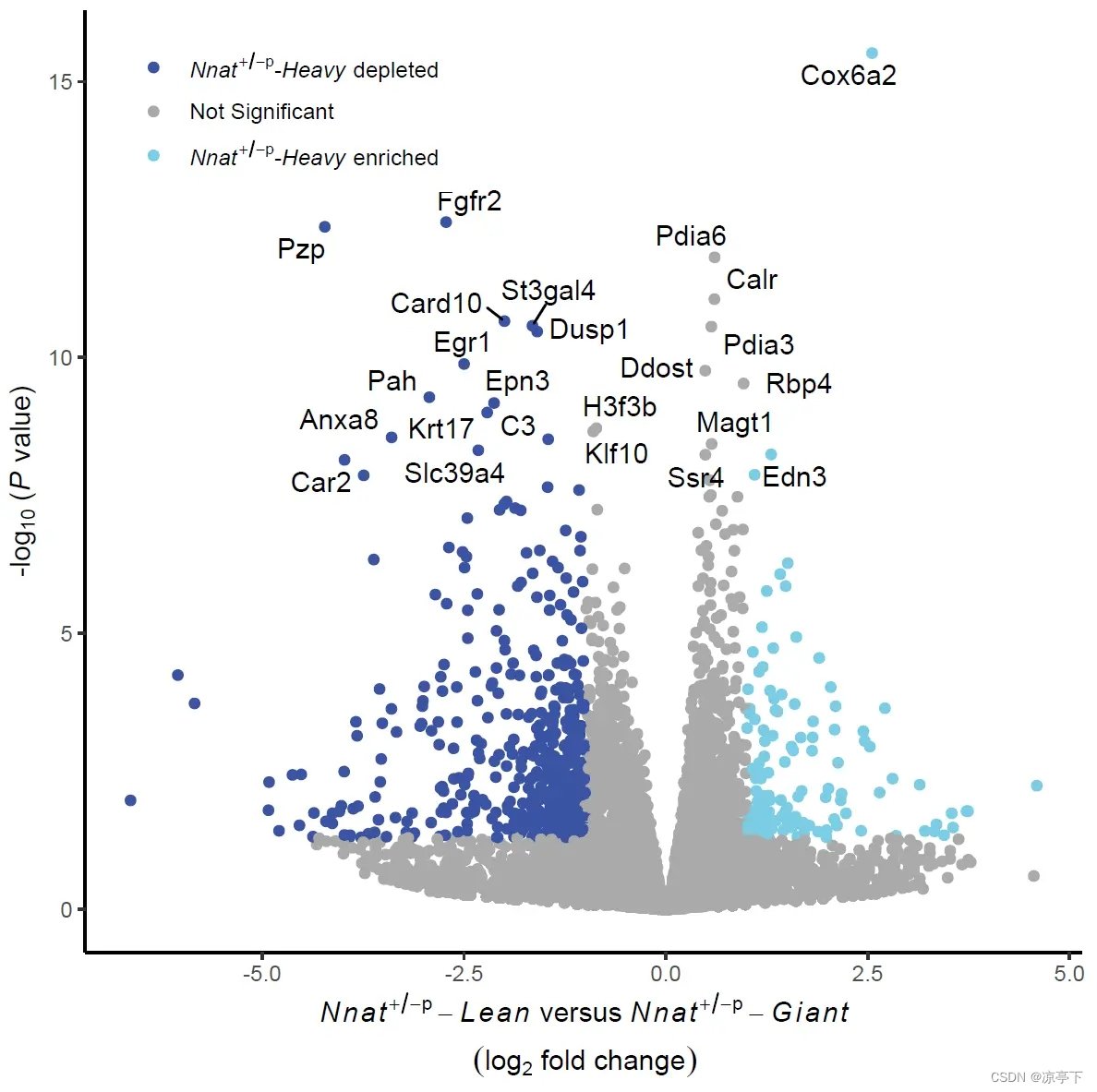
ggplot(data=new.df,aes(x=log2FoldChange,y=-log10(pvalue)))+geom_point(aes(color=change))+scale_color_manual(values = c("Down"="#3a53a4","Not Sig"="#aaaaaa","Up"="#7acde4"),labels=c("Down"=TeX(r"(\textit{Nnat}${^+}$${^/}$${^-}$${^p}$-\textit{Heavy} depleted)"),"Not Sig"="Not Significant","Up" = TeX(r"(\textit{Nnat}${^+}$${^/}$${^-}$${^p}$-\textit{Heavy} enriched)")))+theme_classic()+theme(legend.position = c(0.2,0.9),legend.text.align = 0,legend.title = element_blank())+geom_text_repel(data=new.text.label,aes(x=log2FoldChange,y=-log10(pvalue),label=mgi_symbol))+labs(x=TeX(r"(\overset${\textit{Nnat}{^+}{^/}{^-}{^p}-\textit{Lean}$ versus $\textit{Nnat}{^+}{^/}{^-}{^p}-\textit{Giant}}{(log{_2}$ fold $change)}$)"),y=TeX(r"(-log${_1}{_0}$ {(}\textit{P}{ value}{)})"))
制作封面图
p1<-ggplot(data=new.df,aes(x=log2FoldChange,y=-log10(pvalue)))+geom_point(aes(color=change))+scale_color_manual(values = c("Down"="#3a53a4","Not Sig"="#aaaaaa","Up"="#7acde4"),labels=c("Down"=TeX(r"(\textit{Nnat}${^+}$${^/}$${^-}$${^p}$-\textit{Heavy} depleted)"),"Not Sig"="Not Significant","Up" = TeX(r"(\textit{Nnat}${^+}$${^/}$${^-}$${^p}$-\textit{Heavy} enriched)")))+theme_classic()+theme(legend.position = c(0.2,0.9),legend.text.align = 0,legend.title = element_blank())+geom_text_repel(data=new.text.label,aes(x=log2FoldChange,y=-log10(pvalue),label=mgi_symbol))+labs(x=TeX(r"(\overset${\textit{Nnat}{^+}{^/}{^-}{^p}-\textit{Lean}$ versus $\textit{Nnat}{^+}{^/}{^-}{^p}-\textit{Giant}}{(log{_2}$ fold $change)}$)"),y=TeX(r"(-log${_1}{_0}$ {(}\textit{P}{ value}{)})"))p2<-ggplot(data=new.df,aes(x=log2FoldChange,y=-log10(pvalue)))+geom_point(aes(color=change))+scale_color_manual(values = c("Down"="red","Not Sig"="#aaaaaa","Up"="darkgreen"),labels=c("Down"=TeX(r"(\textit{Nnat}${^+}$${^/}$${^-}$${^p}$-\textit{Heavy} depleted)"),"Not Sig"="Not Significant","Up" = TeX(r"(\textit{Nnat}${^+}$${^/}$${^-}$${^p}$-\textit{Heavy} enriched)")))+theme_classic()+theme(legend.position = c(0.2,0.9),legend.text.align = 0,legend.title = element_blank())+geom_text_repel(data=new.text.label,aes(x=log2FoldChange,y=-log10(pvalue),label=mgi_symbol))+labs(x=TeX(r"(\overset${\textit{Nnat}{^+}{^/}{^-}{^p}-\textit{Lean}$ versus $\textit{Nnat}{^+}{^/}{^-}{^p}-\textit{Giant}}{(log{_2}$ fold $change)}$)"),y=TeX(r"(-log${_1}{_0}$ {(}\textit{P}{ value}{)})"))library(patchwork)
pdf(file = "Rplot03.pdf",width = 14.1,height = 6)
p1+p2
dev.off()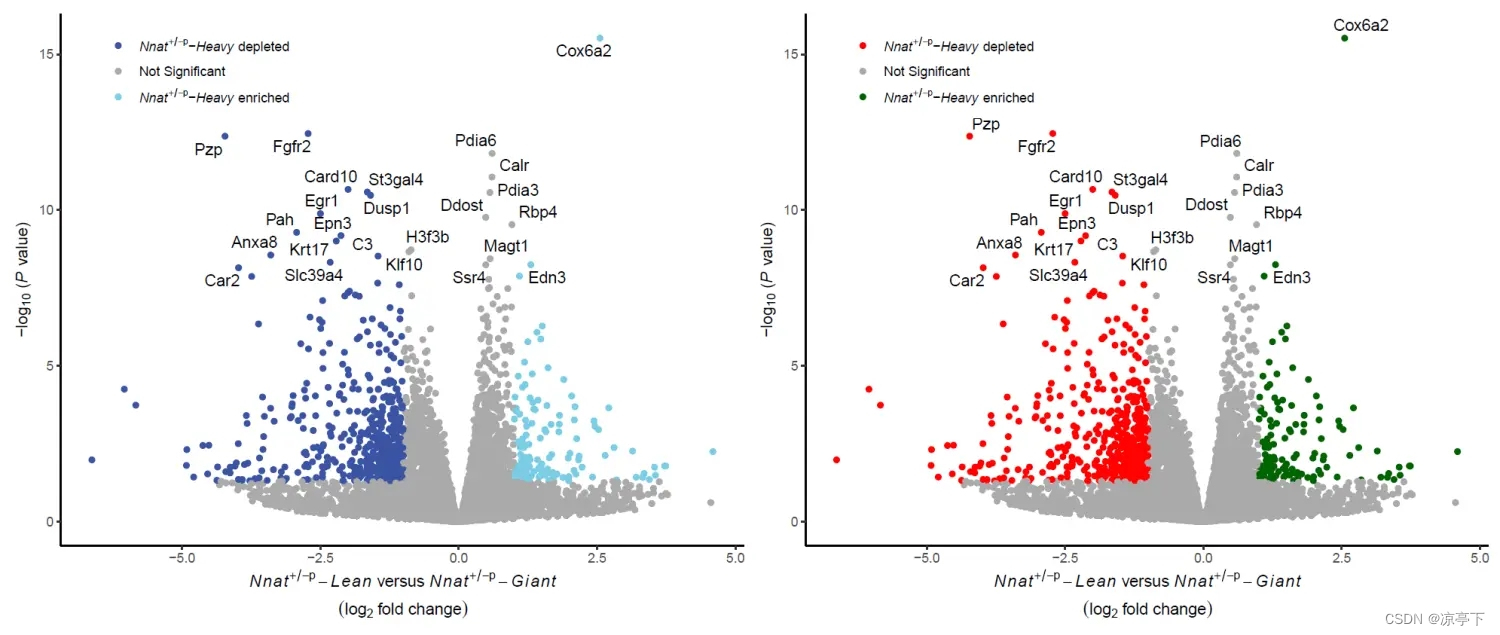
示例数据和代码可以给推文点赞 点击在看 最后留言获取
相关文章:

跟着NatureMetabolism学作图:R语言ggplot2转录组差异表达火山图
论文 Independent phenotypic plasticity axes define distinct obesity sub-types https://www.nature.com/articles/s42255-022-00629-2#Sec15 s42255-022-00629-2.pdf 论文中没有公开代码,但是所有作图数据都公开了,我们可以试着用论文中提供的数据…...
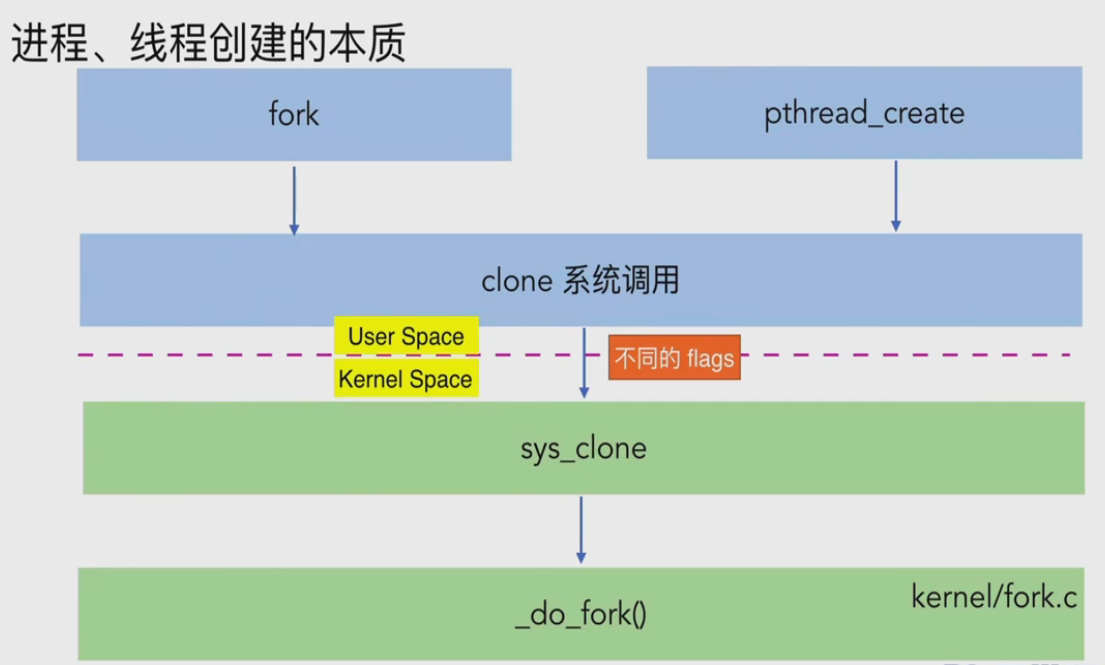
Linux进程与线程的内核实现
进程描述符task_struct 进程描述符(struct task_struct)pid与tgid进程id编号分配规则内存管理mm_struct进程与文件,文件系统 进程,线程创建的本质 clone函数原型线程创建的实现进程创建的实现 总结 进程描述符task_struct 进程描述符(st…...
Flink转换算子(Transformation))
Flink学习之旅:(四)Flink转换算子(Transformation)
1.基本转换算子 基本转换算子说明映射(map)将数据流中的数据进行转换,形成新的数据流过滤(filter)将数据流中的数据根据条件过滤扁平映射(flatMap)将数据流中的整体(如:集…...
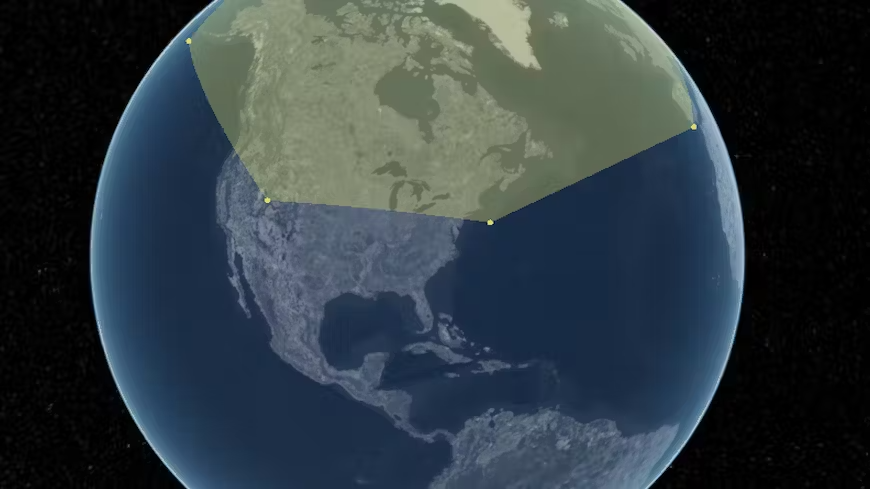
CesiumJS 中绘制大多边形
本文翻译自Cesium官方,有改动。 本文中提及到的“大多边形”就如下图所示。 在Cesium的早期版本和一些引擎中,我们绘制这种跨度比较大的多边形,经常会看到一些奇怪的冲突问题,如下图所示。 要渲染任何几何体,我们必…...

FreeRTOS移植以及任务
FreeRTOS移植 1.在sys.h中需要把SYSTEM_SUPPORT_OS 改为 1,支持我们使用 FreeRTOS //0,不支持 os //1,支持 os #define SYSTEM_SUPPORT_OS 1 //定义系统文件夹是否支持 OS2.出现报错 …\SYSTEM\usart\usart.c(6): error: #5: cannot open source input file “incl…...
)
笙默考试管理系统-MyExamTest----codemirror(41)
笙默考试管理系统-MyExamTest----codemirror(40) 目录 一、 笙默考试管理系统-MyExamTest 二、 笙默考试管理系统-MyExamTest 三、 笙默考试管理系统-MyExamTest 四、 笙默考试管理系统-MyExamTest 五、 笙默考试管理系统-MyExamTest 笙默考试…...

C#数据结构--数组和ArrayList
目录 本章目录: 2.1 数组基本概念 2.1.1 数组的声明和初始化 2.1.2 数组元素的设置和存取访问 2.1.4 多维数组 2.1.5 参数数组 2.2ArrayList 类 2.2.1ArrayList 类的成员 2.2.2 应用 ArrayList 类 数组和ArrayList之间的区别以及使用的场景 数组…...

Stable Diffusion WebUI扩展adetailer安装及功能介绍
ADetailer是Stable Diffusion WebUI的一个扩展,类似于检测细节器。 目录 安装地址 如何安装 1. Windows系统 (1)手动安装 (2)一体机...

Linux安装MINIO
MINIO简介MINIO目录 mkdir -p /opt/minio/data && cd /opt/minio MINIO下载 wget https://dl.minio.org.cn/server/minio/release/linux-amd64/minio MINIO授权 chmod x minio MINIO端口 firewall-cmd --zonepublic --add-port7171/tcp --permanent && firewal…...

Java架构师分布式搜索架构
目录 1 导学1.1 初识Elasticsearch1.1.1 Elasticsearch的作用1.1.2 ELK技术栈1.1.3 Elasticsearch和lucene1.1.4.为什么不是其他搜索技术?1.1.5.总结2 Elasticsearch快速建立知识体系3 Elasticsearch和MySQL实体建立联系3.1.mapping映射属性3.2 数据分组聚合3.2.1.聚合的种类3…...
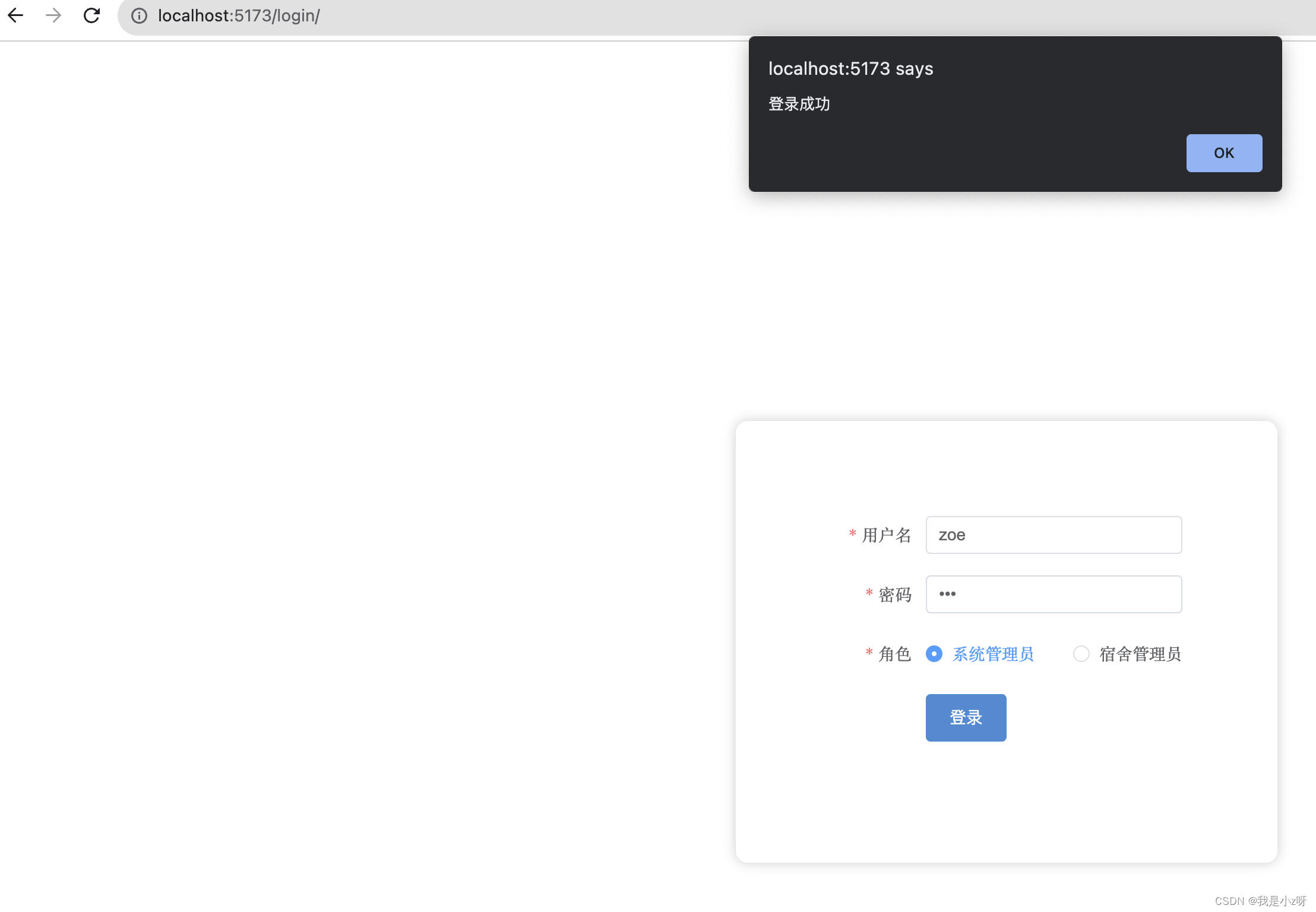
简单宿舍管理系统(springboot+vue)
简单宿舍管理系统(springbootvue) 1.创建项目1.前端2.数据库3.后端 2.登陆1.前端1.准备工作2.登陆组件3.配置 2.后端1.链接数据库2.创建用户实体类3.数据操作持久层1.配置2.内容3.测试 4.中间业务层1.异常2.业务实现3.测试 5.响应前端控制层 3.前后对接4…...

Socks5代理、IP代理的关键作用
Socks5代理与SK5代理:网络安全的卫士 Socks5代理作为一项先进的代理协议,其多协议支持、身份验证功能以及UDP支持使其成为网络安全的重要支持者。 IP代理:隐私保护与无限访问的利器 IP代理技术通过隐藏真实IP地址,保护用户隐私…...

前端 CSS 经典:box-shadow
1. 基础属性 /* box-shadow: h-shadow v-shadow blur spread color inset; */ box-shadow: 10px 10px 2px 2px red inset; h-shadow: 必填,水平阴影的位置,允许负值 v-shadow: 必填,垂直阴影的位置,允许负值 blur: 可选ÿ…...

使用数组方法打印出 1 - 10000 之间的所有对称数。例如:121、1331等
(我从别的人那复制的,原文章请点击此处) 源代码: function getNum (start, end) {var arr [];for(var i start; i < end; i) {if (i.toString() i.toString().split().reverse().join() && i.toString().length &…...
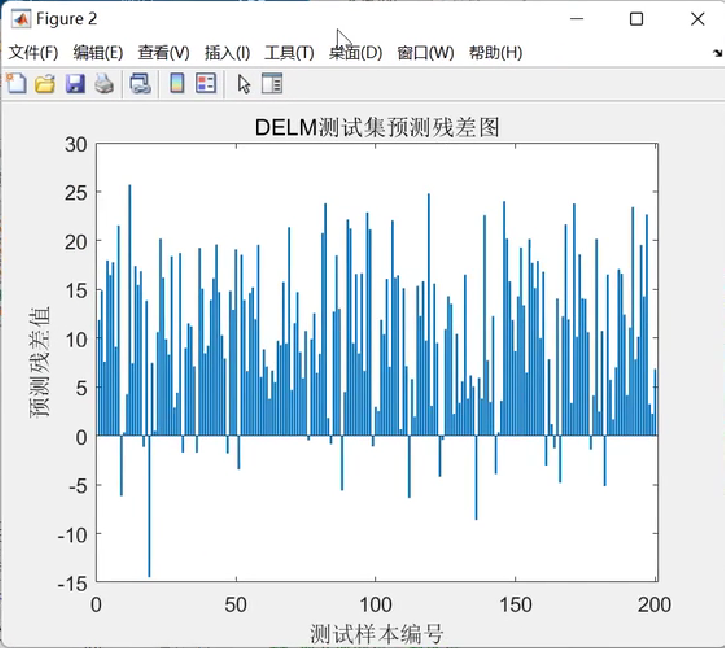
DELM深度极限学习机回归预测研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Spark大数据分析与实战笔记(第一章 Scala语言基础-5)
文章目录 每日一句正能量章节概要1.5 Scala的模式匹配与样例类1.5.1 模式匹配字符匹配匹配字符串守卫匹配类型匹配数组、元组、集合 1.5.2 样例类 课外补充偏函数 每日一句正能量 “成功的秘诀,在于对目标的执着追求。”——爱迪生 无论是在工作、学习、还是生活中&…...

shell学习脚本04(小滴课堂)
他就可以直接读出来了。不需要在sh后面加参数。 可以用-s隐藏内容: 可以用-t进行指定几秒后显示。 -n限制内容长度。 输入到长度为5自动打印。 我们把-s放到-p后面的话: 这样会出错。 如果最后加5m会一直闪烁。 大家可以按照需求自行使用。...
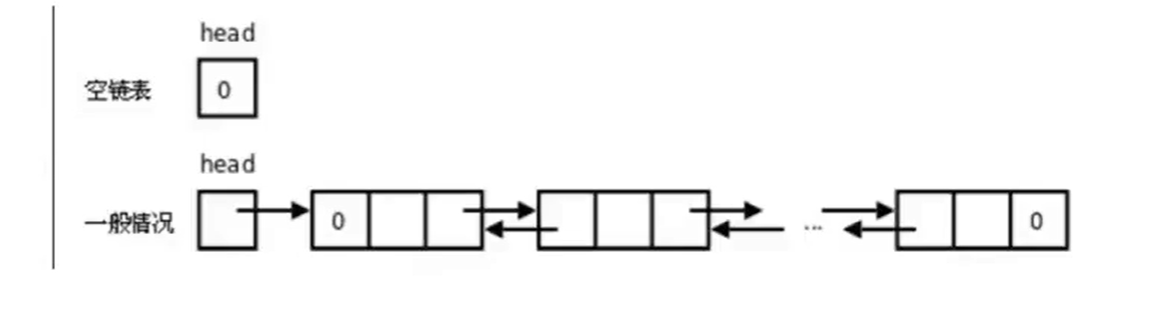
Python数据结构(链表)
Python数据结构(链表) 单向链表 单向链表也叫单链表,是链表中最简单的一种形式,它的每个节点包含两个域,一个信息域(元素域)和一个链接域。这个链接指向链表中的下一个节点,而最后一个节点的链接域则指向…...
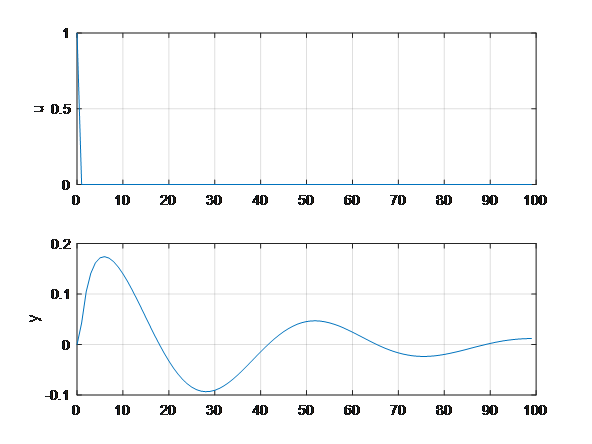
连续/离散的控制系统阶跃测试(包括MATLAB里的step()函数)
阶跃测试 只要是连续时间系统,无论是传递函数还是连续状态空间形式的模型,直接可以用**step()**做阶跃测试;但是对于离散系统而言,不能用step()函数,可以自行编写代码,如下。 1、离散系统:x(k…...
【六:pytest框架介绍】
常见的请求对象requests.get()requests.post()requests.delete()requests.put()requests.request()常见的响应对象reprequests.request()//返回字符串格式数据print(req.text)//返回字节格式数据print(req.content)//返回字典格式数据print(req.json)#状态码print(req.status_c…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...
