LeetCode 1425. 带限制的子序列和【动态规划,单调队列优化】2032
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个整数数组 nums 和一个整数 k ,请你返回 非空 子序列元素和的最大值,子序列需要满足:子序列中每两个 相邻 的整数 nums[i] 和 nums[j] ,它们在原数组中的下标 i 和 j 满足 i < j 且 j - i <= k 。
数组的子序列定义为:将数组中的若干个数字删除(可以删除 0 个数字),剩下的数字按照原本的顺序排布。
示例 1:
输入:nums = [10,2,-10,5,20], k = 2
输出:37
解释:子序列为 [10, 2, 5, 20] 。
示例 2:
输入:nums = [-1,-2,-3], k = 1
输出:-1
解释:子序列必须是非空的,所以我们选择最大的数字。
示例 3:
输入:nums = [10,-2,-10,-5,20], k = 2
输出:23
解释:子序列为 [10, -2, -5, 20] 。
提示:
1 <= k <= nums.length <= 10^5-10^4 <= nums[i] <= 10^4
解法 动态规划+单调队列优化
我们用 f ( i ) f(i) f(i) 表示在数组的前 i i i 个数中进行选择,并且恰好选择了第 i i i 个数,可以得到的最大和。那么 f ( i ) f(i) f(i) 的状态转移分为两种:
- 如果我们在前 i i i 个数中只选择了 n u m s [ i ] nums[i] nums[i] ,那么和即为;
f [ i ] = nums [ i ] f[i] = \textit{nums}[i] f[i]=nums[i] - 如果我们还选择了其它的数,那么我们可以枚举上一个选择的数 n u m s [ j ] nums[j] nums[j] ,并通过 f [ j ] f[j] f[j] 进行状态转移。具体地,根据题目的要求,相邻两个被选择的整数在数组中的下标之差必须小于等于 k k k ,也就是 0 < i − j ≤ k 0 < i - j \leq k 0<i−j≤k ,因此可以写出如下的状态转移方程:
f [ i ] = max max ( i − k , 0 ) ≤ j < i ( f [ j ] ) + nums [ i ] f[i] = \max_{\max(i-k, 0) \leq j < i}(f[j]) + \textit{nums}[i] f[i]=max(i−k,0)≤j<imax(f[j])+nums[i]
将两种情况写在一起,就可以得到状态转移方程:
f [ i ] = max ( max max ( i − k , 0 ) ≤ j < i ( f [ j ] ) , 0 ) + nums [ i ] f[i] = \max\left(\max_{\max(i-k, 0) \leq j < i}(f[j]), 0\right) + \textit{nums}[i] f[i]=max(max(i−k,0)≤j<imax(f[j]),0)+nums[i]
这个状态转移方程看上去很吓人,但我们可以从最简单的方法开始想起。对于每一个 f ( i ) f(i) f(i),我们只要枚举与 i i i 的差值是否小于等于 k k k 的所有 j j j ,并在这些 j j j 中选择一个最大的 f [ j ] f[j] f[j] 进行状态转移即可。如果最大的 f [ j ] f[j] f[j] 小于 0 0 0 ,那么我们不进行状态转移,只选择 n u m s [ i ] nums[i] nums[i] 。
然而这样做的时间复杂度为 O ( n k ) O(nk) O(nk) ,会超出时间限制,因为枚举 i i i 和 j j j 的时间复杂度分别为 O ( n ) O(n) O(n) 和 O ( k ) O(k) O(k) 。那么我们如何进行优化呢?
观察上面的状态转移方程,我们大致有一个这样的想法:对于每一个 i i i,我们选择的都是满足要求的 j j j 中最大的 f [ j ] f[j] f[j] 值。那么如果 f ( i ) f(i) f(i) 是从 f [ j ] f[j] f[j] 转移而来的,只要 j j j 与 i + 1 i+1 i+1 相差不超过 k k k , f [ i + 1 ] f[i+1] f[i+1] 也很有可能从 f [ j ] f[j] f[j] 转移而来。
这个想法也就是我们熟知的「单调栈」或者「单调队列」。不妨试着使用它们对状态转移方程进行优化。
单调队列优化
在从小到大枚举 i i i 的过程中,假设我们有两个位置 j 1 j_1 j1 和 j 2 j_2 j2 可以考虑进行转移,并且 j 1 < j 2 j_1 < j_2 j1<j2 。如果 f [ j 1 ] ≤ f [ j 2 ] f[j_1] \leq f[j_2] f[j1]≤f[j2] ,那么我们可以断定,对于以后会枚举到的所有 i i i , j 1 j_1 j1 都不会优于 j 2 j_2 j2 了。换句话说,我们可以直接「扔掉」 j 1 j_1 j1 ,因为它不会转移到后续的任何状态。
这是为什么呢?我们这样想,对于任意一个满足 j 1 < j 2 < i j_1 < j_2 < i j1<j2<i 的 i i i ,如果它从 j 1 j_1 j1 转移而来,那么它一定也能从 j 2 j_2 j2 转移而来,这是因为转移的唯一要求是 i i i 和 j j j 相差不超过 k k k ,那么在 i i i 和 j 1 j_1 j1 满足要求的前提下, i i i 和 j 2 j_2 j2 也一定满足要求。并且 f [ j 1 ] ≤ f [ j 2 ] f[j_1] \leq f[j_2] f[j1]≤f[j2] ,那么 j 2 j_2 j2 一定不比 j 1 j_1 j1 差。那么在「有生之年」,我们在进行转移时就不需要考虑 j 1 j_1 j1 了。
因此,我们可以考虑使用一个「单调栈」来维护所有可能会考虑的 j j j 。为什么它是一个「栈」呢?我们来看看它的具体维护方法:
- 假设我们当前维护了这样的一个「单调栈」,它包含 j 1 , j 2 , ⋯ , j x j_1, j_2, \cdots, j_x j1,j2,⋯,jx ,并且 j 1 < j 2 < ⋯ < j x j_1 < j_2 < \cdots < j_x j1<j2<⋯<jx 。根据上面提到的性质,必定有 f [ j 1 ] > f [ j 2 ] > ⋯ > f [ j x ] f[j_1] > f[j_2] > \cdots > f[j_x] f[j1]>f[j2]>⋯>f[jx] 。如果我们需要将一个新的 j j j 值 j y j_y jy 放入单调栈中,那么我们从栈顶元素开始考虑:如果 f [ j x ] ≤ f [ j y ] f[j_x] \leq f[j_y] f[jx]≤f[jy] ,那么根据上文的推导,我们可以直接「扔掉」 j x j_x jx ,也就是将栈顶元素弹出。
- 以此类推,我们可以不断地弹出栈顶元素,直到栈顶元素对应的 f f f 值大于 f [ j y ] f[j_y] f[jy] 或者栈为空。此时我们再将 j y j_y jy 放入栈顶,就得到了一个新的「单调栈」。
- 这样以来,栈底的 j j j 对应着最大的 f [ j ] f[j] f[j] 值,我们用它来转移到 f ( i ) f(i) f(i) 就行了。
然而,这样的设计存在两个问题:
- 我们使用的是一个「栈」,在仅使用栈的 API 的前提下,而我们并没有办法获得「栈底」的元素;
- 栈底的 j j j 可能与当前的 i i i 值的差大于 k k k 。
因此,我们需要用「队列」来代替栈,即单调队列。
- 对于第一个问题,我们可以通过获取队首元素解决。
- 对于第二个问题,我们要做的是不断地将队首的元素弹出,直到队首的 j j j 与当前的 i i i 值的差小于 k k k 为止。由于我们需要「取出队首元素」「取出队尾元素」这两种操作,因此我们使用的是「双端队列」。
算法流程——我们使用单调队列进行优化的动态规划的算法流程如下:
- 我们用一个双端队列来维护所有可能会进行转移的 j j j 值。在队列中,这些 j j j 值单调递增,但是它们对应的 f [ j ] f[j] f[j] 值是单调递减的;
- 我们从小到大枚举 i i i 。在枚举的每一步中,单调队列的队首元素就是最优的转移选择。但由于题目要求相邻的两个数的位置最多间隔 k k k ,因此我们需要从队首弹出元素,直到队首的 j j j 值与 i i i 的差值小于等于 k k k ;
- 在计算出 f ( i ) f(i) f(i) 后,我们将 i i i 根据规则放入单调队列的队尾。在放入之前,可能会弹出若干队尾的元素。
- 最终的答案即为所有 f ( i ) f(i) f(i) 中的最大值。
class Solution {
public:int constrainedSubsetSum(vector<int>& nums, int k) {int n = nums.size();// 存储动态规划结果的数组vector<int> f(n);// 我们直接放入f[0]的值,防止处理边界情况f[0] = nums[0];// 单调队列deque<int> q;// 一开始唯一的j为0q.push_back(0);int ans = nums[0];for (int i = 1; i < n; ++i) {// 如果队首的j与i的差值大于k,则不满足要求,弹出while (!q.empty() && i - q.front() > k) q.pop_front();// 此时队首的j即为最优的j值f[i] = max(f[q.front()], 0) + nums[i];ans = max(ans, f[i]);// 维护队列的单调性,不断从队尾弹出元素while (!q.empty() && f[i] >= f[q.back()]) q.pop_back();// 将i作为之后的新j值放入队尾q.push_back(i);}return ans;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) ,其中 n n n 是数组 nums \textit{nums} nums 的长度。每一个数组下标都被放入队列一次,并且被弹出队列最多一次,因此处理队列的时间总计为 O ( n ) O(n) O(n) ,与枚举 i i i 的时间 O ( n ) O(n) O(n) 相加仍然为 O ( n ) O(n) O(n) 。
- 空间复杂度: O ( n ) O(n) O(n) ,数组 f f f 和单调队列各需要 O ( n ) O(n) O(n) 的空间。
相关文章:

LeetCode 1425. 带限制的子序列和【动态规划,单调队列优化】2032
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
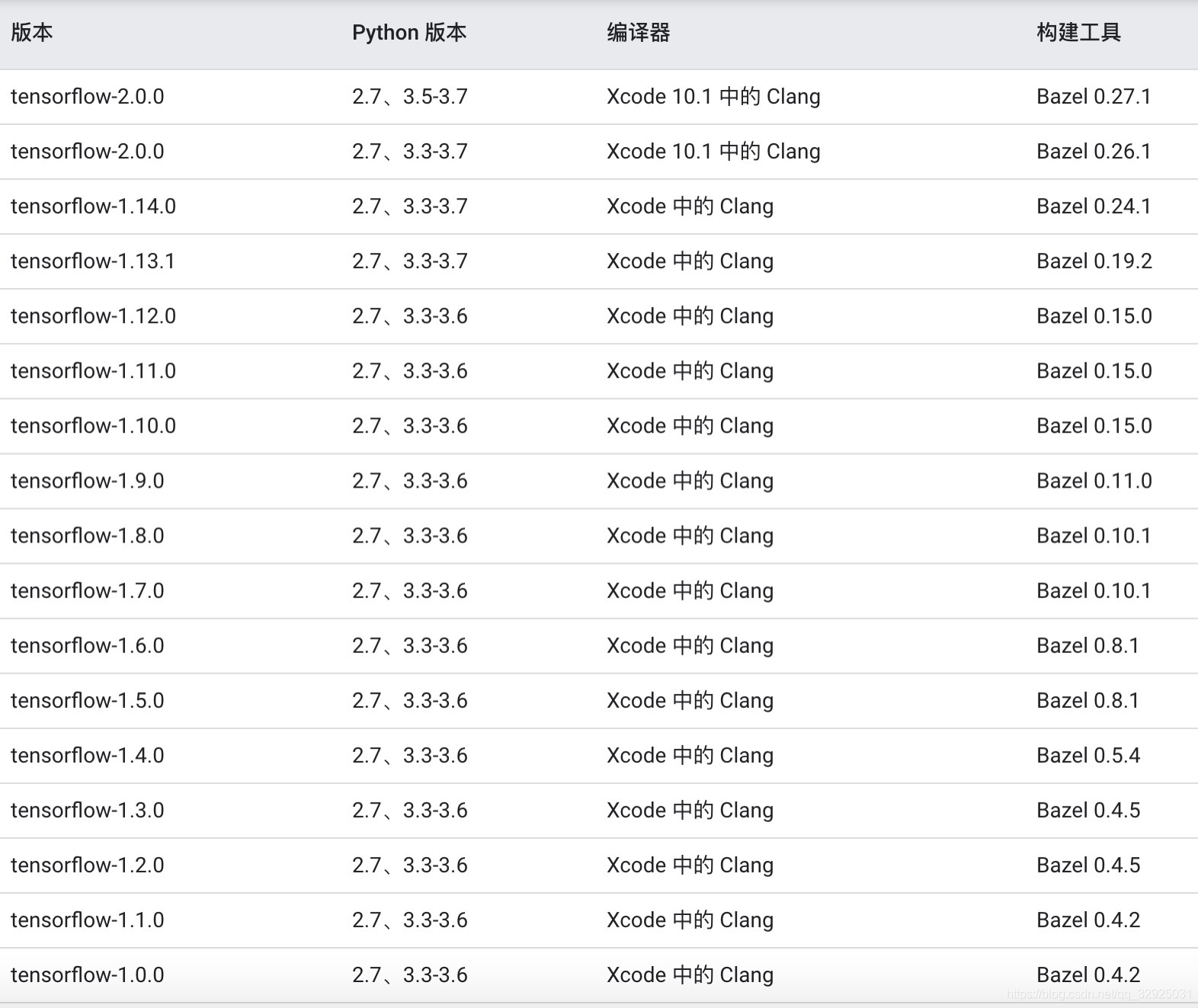
强化学习问题(7)--- Python和Pytorch,Tensorflow的版本对应
1.问题 之前下载的python3.8,在对应Pytorch和Tensorflow时没太在意版本,在运行一些代码时,提示Pytorch和Tensorflow版本过高,直接降下来,有时候又和Python3.8不兼容,所以又在虚拟环境搞一个Pyhon3.7&#x…...
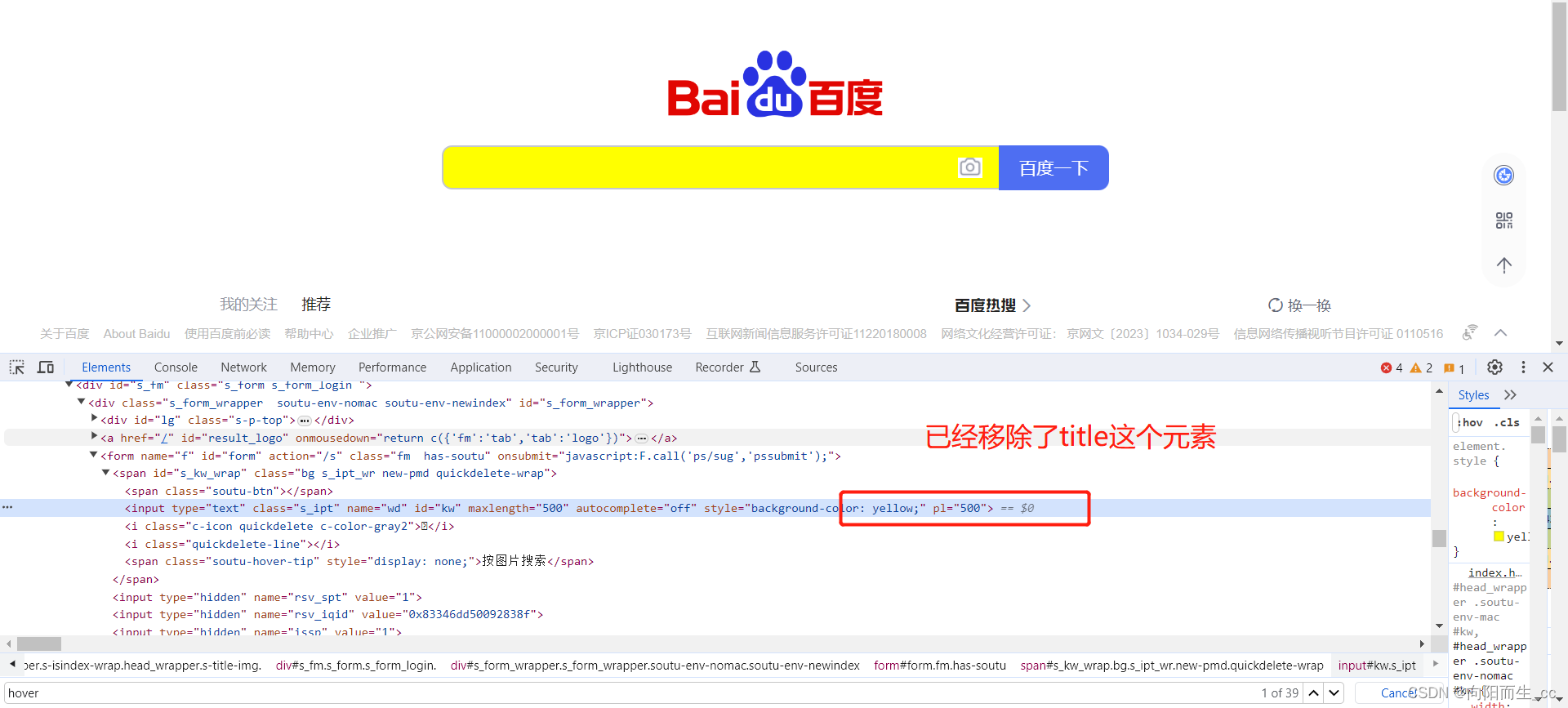
Python —— UI自动化之使用JavaScript进行元素点亮、修改、点击元素
1、JavaScript点亮元素 在控制台通过JavaScript语言中对元素点亮效果如下: 将这个语句和UI自动化结合,代码如下: locator (By.ID,"kw") # 是元组类型 web_element WebDriverWait(driver,5,0.5).until(EC.visibility_of_eleme…...

input表单的23个type属性
在HTML中,<input>标签用于创建输入框。type属性用于指定输入框的类型。以下是23个可能的type属性及其用途: text:普通文本输入框。password:密码输入框,输入的内容会显示为圆点或星号。email:电子邮…...

优先级总结
目录 越小越优先 1.路由协议 2.路由开销 3.STP 4.Ethernet-trunk(LACP) 越大越优先 1.VRRP 2.Router-id 3.DR/BDR 越小越优先 1.路由协议 取值范围:0~255 直连路由0 静态路由/默认路由60 RIP路由100 OSPF路由10或150 BGP路由255 2…...
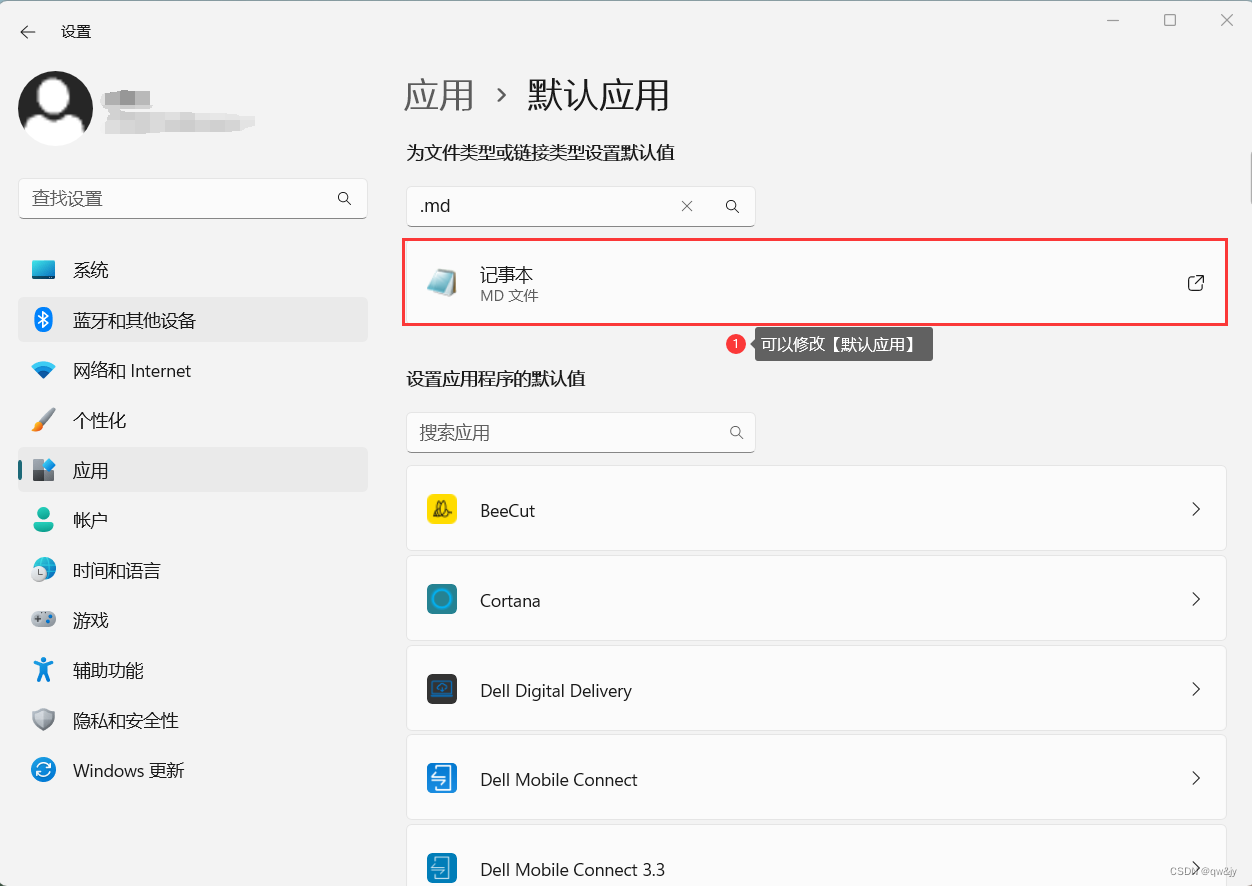
Windows 11中无法通过默认应用更改文件关联
这里写自定义目录标题 现象解决方法 这里以.md格式文件为例。 现象 在 Windows 11 计算机上安装第三方软件后,关联 JPG、JPE、JPEG、PNG、MPG、MPEG、MD 等文件类型和其他文件类型的能力可能会受到阻碍。以下是尝试更改上述文件类型的文件关联时可能遇到的问题。 …...
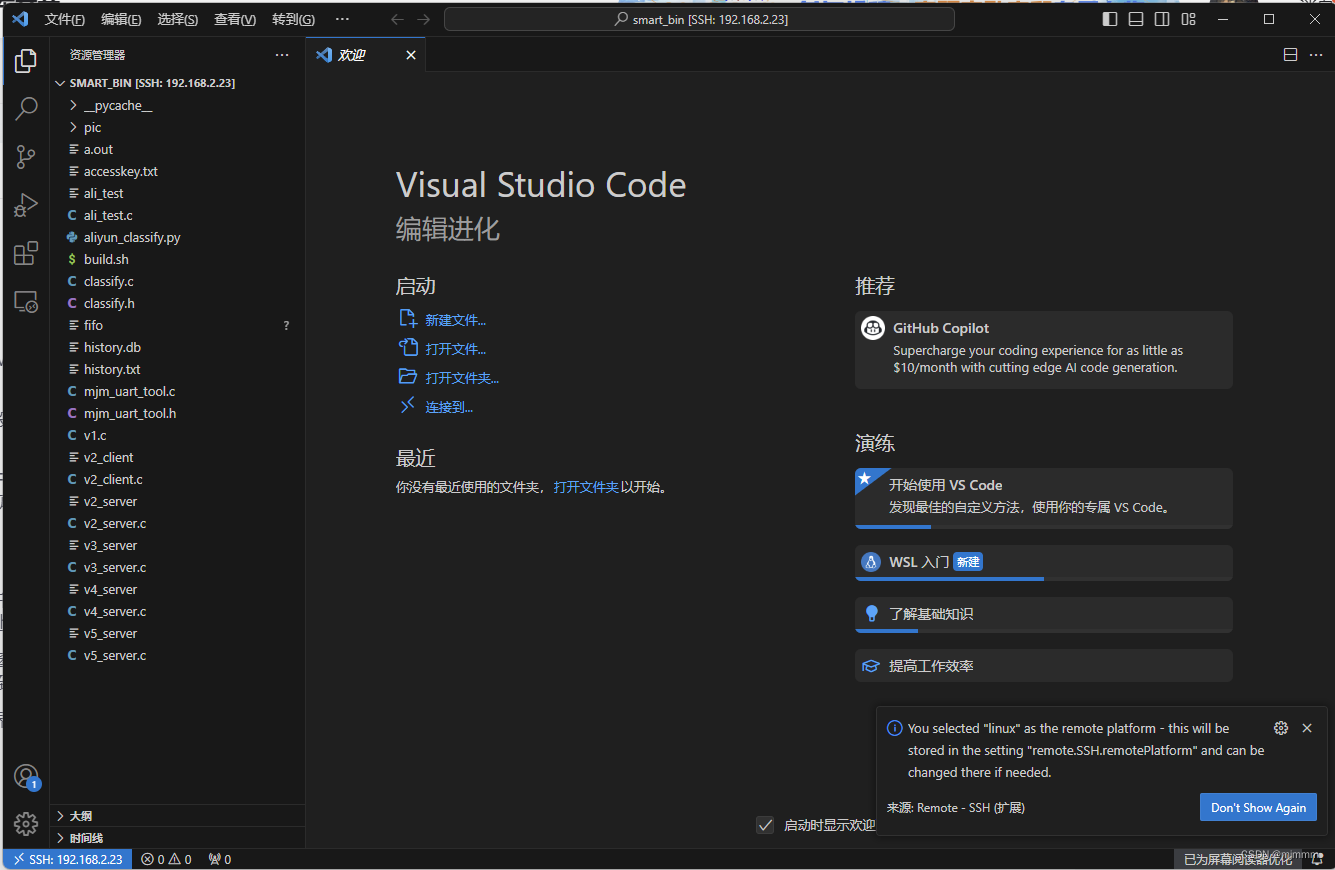
小插曲 -- 使用Visual Studio Code远程连接香橙派
在之前的学习中,代码的修改和保存都依赖于“vi”指令,而不得不承认vi指令的编辑界面非常原始,所以,如果可以将代码编辑放到更友好的环境里进行无疑是一件大快人心的事情。 本节介绍如何通过Visual Studio Code来进行远程连接: Vi…...

留意差距:弥合网络安全基础设施的挑战
您最近一直在关注日益增加的网络威胁吗?如果您发现自己沉浸在 IT 或技术中,那么您可能会永远追求与时俱进。每天都会出现新的漏洞,这对保持消息灵通提出了巨大的挑战。 构建和维护能够应对复杂攻击者的网络安全基础设施所面临的挑战是真实存…...

【vSphere 8 自签名证书】企业 CA 签名证书替换 vSphere Machine SSL 证书Ⅰ—— 生成 CSR
目录 替换拓扑图证书关系示意图说明 & 关联博文 1. 默认证书截图2. 使用certificate-manager生成CSR2.1 创建存放CSR的目录2.2 记录PNID和IP2.3 生成CSR2.4 验证CSR 参考资料 替换拓扑图 证书关系示意图 默认情况下,VMCA 与 Machine SSL的关系是 本系列博文要…...

TypeScript中extends的用法
介绍 extends 关键字在 TypeScript 中有多种应用,包括泛型约束、继承类、接口继承和条件类型。通过灵活使用 extends,TypeScript 提供了丰富的工具来增强类型安全性,使代码更具表现力和可维护性。 1. 约束接口的继承 extends 关键字也可用于…...
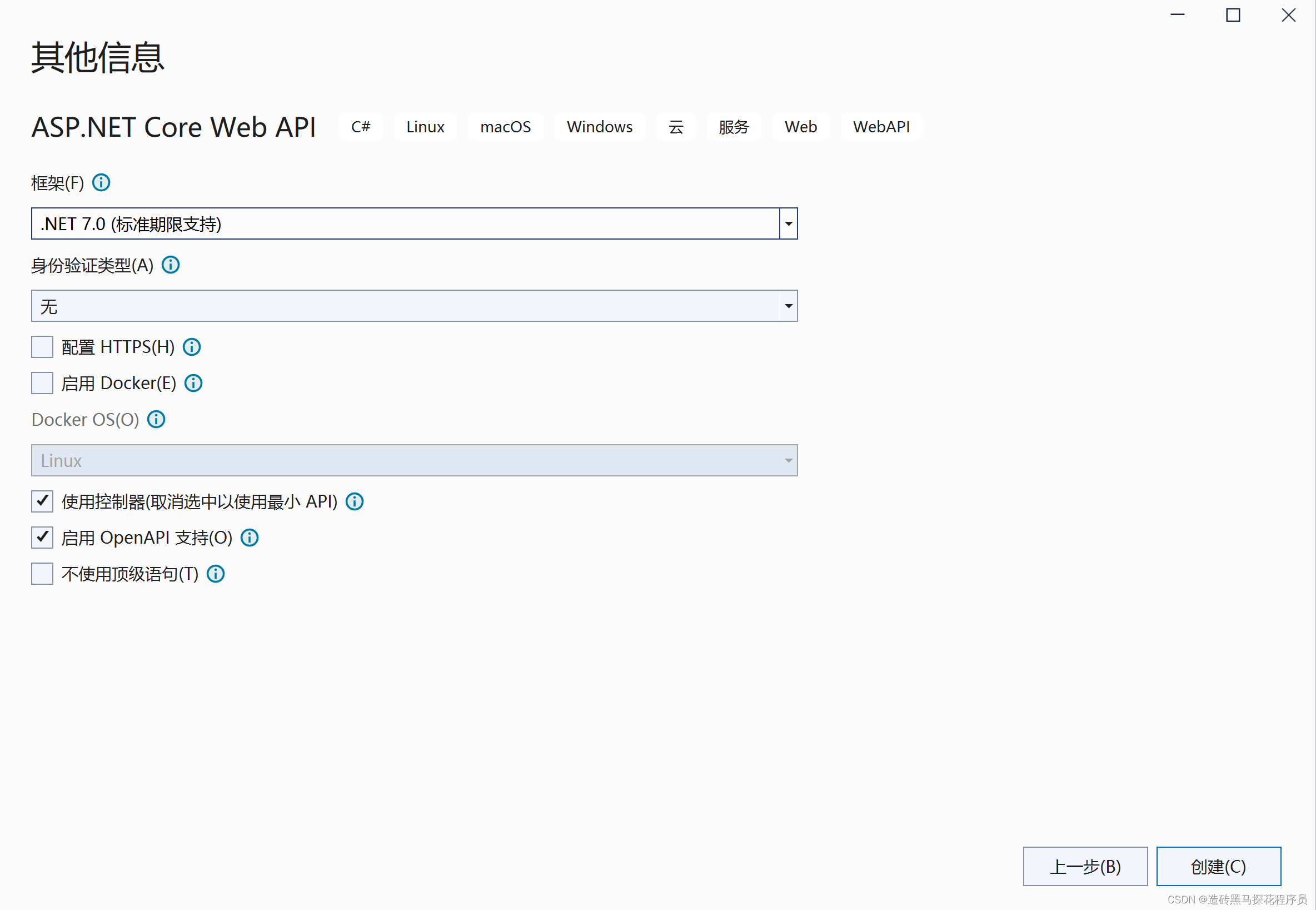
手把手创建属于自己的ASP.NET Croe Web API项目
第一步:创建项目的时候选择ASP.NET Croe Web API 点击下一步,然后配置: 下一步:...
【Javascript】数组的基本操作
目录 声明 字面量形式 构造函数声明 访问数组中的元素 数组的长度 增删改查 增 通过索引添加数据 在数组后面添加数据 在数组前添加数据 删 删除数组中最后一个元素 删除数组中第一个元素 改 查 数组是⼀种列表对象,它的原型中提供了遍历和修改元素的…...
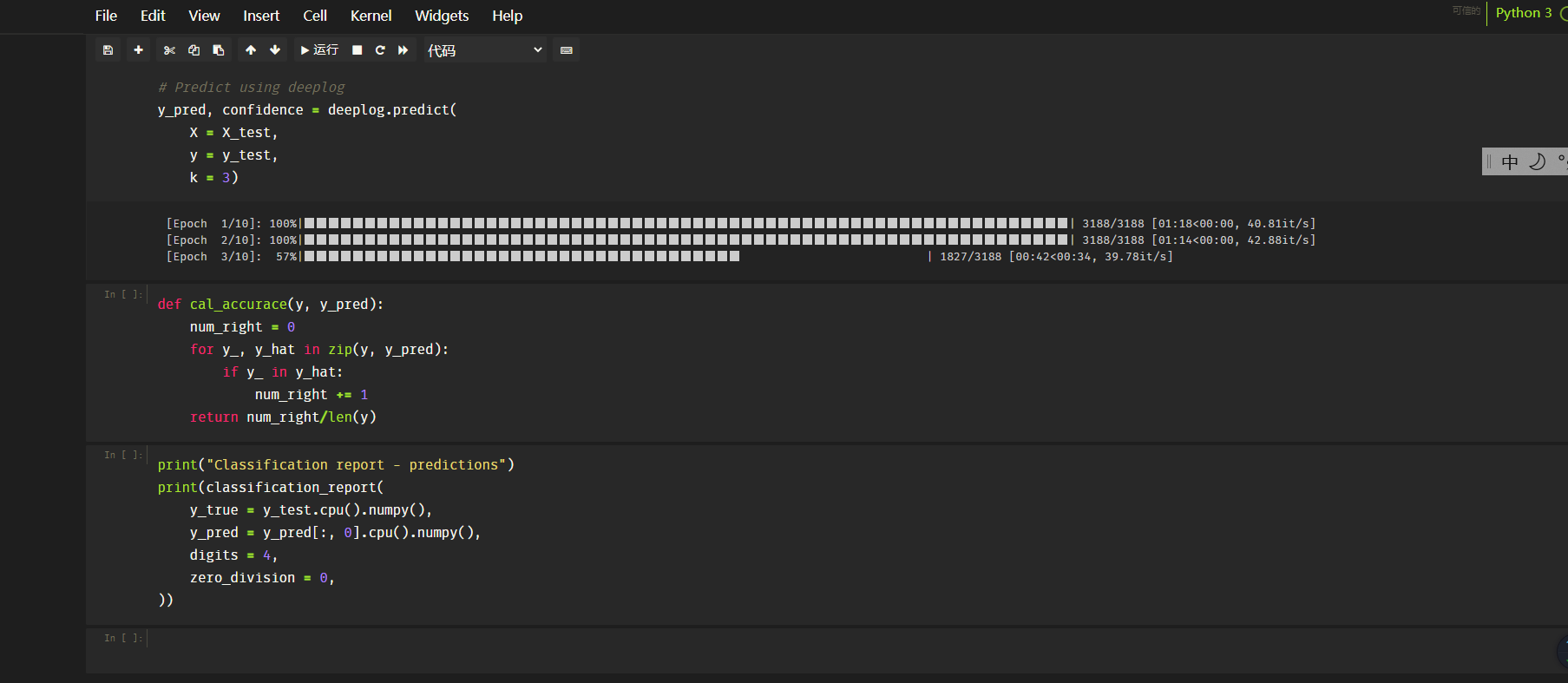
Jupyter Notebook 设置黑色背景主题
Jupyter Notebook 设置黑色背景主题 # 包安装 pip install jupyterthemes -i https://mirrors.aliyun.com/pypi/simple pip install --upgrade jupyterthemes # 查看可用主题 jt -l # monokai暗背景,-f(字体) -fs(字体大小) -cellw(占屏比或宽度) -ofs(输出段的字…...

1 Go的前世今生
概述 Go语言正式发布于2009年11月,由Google主导开发。它是一种针对多处理器系统应用程序的编程语言,被设计成一种系统级语言,具有非常强大和有用的特性。Go语言的程序速度可以与C、C相媲美,同时更加安全,支持并行进程。…...

面试-Redis-缓存击穿
问:什么是缓存击穿 ? 怎么解决 ? 答:缓存击穿的意思是对于设置时间过期的key,当key过期时,恰好有大量对这个key的请求发送过来,此时这些请求发现这个key过期,就会打到数据库加载数据并设置缓存ÿ…...
)
80个国内可用的Chatgpt网页版(2023.10.21更新)
ChatGPT:革命性的人工智能语言模型 ChatGPT,一款能够与人类进行自然流畅对话的人工智能语言模型,通过大量训练数据和先进算法,展现出卓越的自然语言处理能力。它能理解并回应人类问题,提供准确、连贯且有意义的答案&a…...
Android 10.0 Launcher3定制化之动态时钟图标功能实现
1.概述 在10.0的系统产品rom定制化开发中,在Launcher3中的定制化的一些功能中,对于一些产品要求需要实现动态时钟图标功能,这就需要先绘制时分秒时针表盘,然后 每秒刷新一次时钟图标,时钟需要做到实时更新,做到动态时钟的效果,接下来就来分析这个功能的实现 如图: 2.动…...
HTTPS、SSL/TLS,HTTPS运行过程,RSA加密算法,AES加密算法
1、为什么网站要使用安全证书 我们所处的网络环境是复杂多样的,大致分为两类,一类是可信的网络服务商,比如直接连的电信运营商的网络,网线,4G,5G;另一类是不可信的网络,比如WIFI&am…...

python之Scrapy爬虫案例:豆瓣
运行命令创建项目:scrapy startproject scrapySpider进入项目目录:cd .\scrapySpider\运行命令创建爬虫:scrapy genspider douban movie.douban.com目录结构说明|-- scrapySpider 项目目录 | |-- scrapySpider 项目目录 | | |-- spider…...
2023最新UI酒桌喝酒游戏小程序源码 娱乐小程序源码 带流量主
2023最新UI酒桌喝酒游戏小程序源码 娱乐小程序源码 带流量主 修改增加了广告位,根据文档直接替换,原版本没有广告位 直接上传源码到开发者端即可 通过后改广告代码,然后关闭广告展示提交,通过后打开即可 无广告引流 流量主版…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
