【LeetCode周赛】LeetCode第368场周赛
目录
- 元素和最小的山形三元组 I
- 元素和最小的山形三元组 II
- 合法分组的最少组数
元素和最小的山形三元组 I
给你一个下标从 0 开始的整数数组 nums 。
如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个山形三元组 :
i < j < k
nums[i] < nums[j] 且 nums[k] < nums[j]
请你找出nums中元素和最小的山形三元组,并返回其 元素和 。如果不存在满足条件的三元组,返回 -1 。
示例 1:
输入:nums = [8,6,1,5,3]
输出:9
解释:三元组 (2, 3, 4) 是一个元素和等于 9 的山形三元组,因为:
- 2 < 3 < 4
- nums[2] < nums[3] 且 nums[4] < nums[3]
这个三元组的元素和等于 nums[2] + nums[3] + nums[4] = 9 。可以证明不存在元素和小于 9 的山形三元组。
示例 2:
输入:nums = [5,4,8,7,10,2]
输出:13 解释:三元组 (1, 3, 5) 是一个元素和等于 13 的山形三元组,因为:
- 1 < 3 < 5
- nums[1] < nums[3] 且 nums[5] < nums[3]
这个三元组的元素和等于 nums[1] + nums[3] + nums[5] = 13 。可以证明不存在元素和小于 13 的山形三元组。
示例 3:
输入:nums = [6,5,4,3,4,5]
输出:-1
解释:可以证明 nums 中不存在山形三元组。
提示:
3 < = n u m s . l e n g t h < = 50 3 <= nums.length <= 50 3<=nums.length<=50
1 < = n u m s [ i ] < = 50 1 <= nums[i] <= 50 1<=nums[i]<=50
分析:
因为数据范围很小,所以可以直接按照题目意思进行模拟,遍历每一个三元组,维护一个最小三元组的和即可。时间复杂度 O ( n 3 ) O(n^3) O(n3)。
代码:
class Solution {
public:int minimumSum(vector<int>& nums) {int n=nums.size();int ans=INT_MAX;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){for(int k=j+1;k<n;k++){if(nums[i]<nums[j]&&nums[k]<nums[j])ans=min(ans,nums[i]+nums[j]+nums[k]);}}}if(ans==INT_MAX)ans=-1;return ans;}
};
元素和最小的山形三元组 II
给你一个下标从 0 开始的整数数组 nums 。
如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个山形三元组 :
i < j < k
nums[i] < nums[j] 且 nums[k] < nums[j]
请你找出nums中元素和最小的山形三元组,并返回其 元素和 。如果不存在满足条件的三元组,返回 -1 。
示例 1:
输入:nums = [8,6,1,5,3]
输出:9
解释:三元组 (2, 3, 4) 是一个元素和等于 9 的山形三元组,因为:
- 2 < 3 < 4
- nums[2] < nums[3] 且 nums[4] < nums[3]
这个三元组的元素和等于 nums[2] + nums[3] + nums[4] = 9 。可以证明不存在元素和小于 9 的山形三元组。
示例 2:
输入:nums = [5,4,8,7,10,2]
输出:13 解释:三元组 (1, 3, 5) 是一个元素和等于 13 的山形三元组,因为:
- 1 < 3 < 5
- nums[1] < nums[3] 且 nums[5] < nums[3]
这个三元组的元素和等于 nums[1] + nums[3] + nums[5] = 13 。可以证明不存在元素和小于 13 的山形三元组。
示例 3:
输入:nums = [6,5,4,3,4,5]
输出:-1
解释:可以证明 nums 中不存在山形三元组。
提示:
3 < = n u m s . l e n g t h < = 1 0 5 3 <= nums.length <= 10^{5} 3<=nums.length<=105
1 < = n u m s [ i ] < = 1 0 8 1 <= nums[i] <= 10^{8} 1<=nums[i]<=108
分析:
本题为第一题的加强版,数据范围扩大,使用题一的 O ( n 3 ) O(n^3) O(n3)的方法会TLE,所以我们仔细思考题意,不难想到,要使得一个三元组的和最小,那么对于山顶i,找到i左边的最小值pre[i],和i右边的最小值suf[i],只要pre[i]和suf[i]同时都小于nums[i]的值,那么这就是以i为山顶的三元组的和的最小值。
所以我们可以先进行预处理,遍历一遍数组,维护一个前缀最小值和后缀最小值。时间复杂度为 O ( n ) O(n) O(n)
代码:
class Solution {
public:int minimumSum(vector<int>& nums) {//对每个数找到其前面的最小数和后面的最小数int n = nums.size();vector<int>pre(n+1),suf(n+1);pre[0]=nums[0];suf[n-1]=nums[n-1];for(int i=1;i<n;i++)pre[i]=min(nums[i],pre[i-1]);for(int i=n-2;i>=0;i--)suf[i]=min(nums[i],suf[i+1]);int ans=INT_MAX;for(int i=0;i<n;i++){if(nums[i]>pre[i]&&nums[i]>suf[i])ans=min(ans,pre[i]+nums[i]+suf[i]);}if(ans==INT_MAX)ans=-1;return ans;}
};
合法分组的最少组数
给你一个长度为 n 下标从 0 开始的整数数组 nums 。
我们想将下标进行分组,使得 [0, n - 1] 内所有下标 i 都 恰好 被分到其中一组。
如果以下条件成立,我们说这个分组方案是合法的:
对于每个组 g ,同一组内所有下标在 nums 中对应的数值都相等。
对于任意两个组 g1 和 g2 ,两个组中 下标数量 的 差值不超过 1 。
请你返回一个整数,表示得到一个合法分组方案的 最少 组数。
示例 1:
输入:nums = [3,2,3,2,3]
输出:2
解释:一个得到 2 个分组的方案如下,中括号内的数字都是下标:
组 1 -> [0,2,4]
组 2 -> [1,3]
所有下标都只属于一个组。 组 1 中,nums[0] == nums[2] == nums[4],所有下标对应的数值都相等。
组 2 中,nums[1] == nums[3] ,所有下标对应的数值都相等。
组 1 中下标数目为 3 ,组2 中下标数目为 2 。
两者之差不超过 1 。
无法得到一个小于 2 组的答案,因为如果只有 1 组,组内所有下标对应的数值都要相等。
所以答案为 2 。
示例 2:
输入:nums = [10,10,10,3,1,1]
输出:4
解释:一个得到 2 个分组的方案如下,中括号内的数字都是下标:
组 1 ->[0]
组 2 -> [1,2]
组 3 -> [3]
组 4 -> [4,5]
分组方案满足题目要求的两个条件。 无法得到一个小于 4组的答案。
所以答案为 4 。
提示:
1 < = n u m s . l e n g t h < = 1 0 5 1 <= nums.length <= 10^{5} 1<=nums.length<=105
1 < = n u m s [ i ] < = 1 0 9 1 <= nums[i] <= 10^{9} 1<=nums[i]<=109
分析:
首先我们需要统计每个数字出现的次数,维护在cnt中。
如何判断一个数字可以拆分为k和k+1的组合呢?
比如说cnt[x]=13,k=4,那么13=4+4+4+1,多出来的这一个1可以丢进前面的某一个4中,同理11=4+4+3,不能由k和k+1构成,14=4+4+4+2=5+5+4,15=4+4+4+3=5+5+5,而16=4+4+4+4,不能由5表示了,可以想到,只要cnt[x]/k的值大于等于cnt[x]%k的值,那么其就可以由k和k+1来构成。
那么如何计算最小的分组呢?
不难理解,只要分出的k+1越多,那么分出的组数肯定就越少,即最少可以分出 ⌈ c n t [ x ] k + 1 ⌉ \lceil \frac{cnt[x]}{k+1} \rceil ⌈k+1cnt[x]⌉个组。
因为我们已经确定了能够拆分为k和k+1的组合,p=cnt[x]/k,v=cnt[x]%k,先拆成了p个k,剩下数字v,其实就是v有几个,那么就可以将多少个v个k加一变成k+1。所以直接除以k+1即可得到组数,上取整是因为如果除以k+1有余数,那么这个余数需要补充到有k个数,即组数会多一个。
比如15=5+5+5,16=5+5+5+1=4+4+4+4,13=5+5+3=5+4+4。
最后只需要从min(cnt[x])开始往下枚举k,找到一个满足要求的k即可返回结果。
时间复杂度:枚举cnt中最小的数为k,cnt的size为m, m k ≤ n mk \le n mk≤n,循环的次数最多为km,所以时间复杂度为 O ( n ) O(n) O(n)。
代码:
class Solution {
public:int minGroupsForValidAssignment(vector<int>& nums) {int n = nums.size();unordered_map<int, int>mp;vector<int>cnt;for(int i = 0; i < n ; i++){mp[nums[i]]++;}for(auto &[k,v]:mp)cnt.push_back(v);sort(cnt.begin(),cnt.end());int min_num=cnt[0];//枚举最小的组do{int ans = 0;if(min_num==0)break;for(auto x:cnt){int p = x / min_num;int v = x % min_num;if(p >= v)ans += (x + min_num) / (min_num + 1);else{ans = 0;break;}}if(ans)return ans;}while(min_num--);return 0;}};
相关文章:

【LeetCode周赛】LeetCode第368场周赛
目录 元素和最小的山形三元组 I元素和最小的山形三元组 II合法分组的最少组数 元素和最小的山形三元组 I 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个山形三元组 : i < j < k nums[i] &l…...
【智慧工地源码】基于AI视觉技术赋能智慧工地
伴随着技术的不断发展,信息化手段、移动技术、智能穿戴及工具在工程施工阶段的应用不断提升,智慧工地概念应运而生,庞大的建设规模催生着智慧工地的探索和研发。 建筑施工具有周期长、环境复杂、工序繁杂、人员流动性大等特点,所以…...

云服务器搭建Hadoop分布式
文章目录 1.服务器配置2.Java环境3. 安装Hadoop4. 集群配置5. 编写集群的启动脚本 1.服务器配置 服务器主机名配置115.157.197.82s110核115.157.197.84s210核115.157.197.109s310核115.157.197.31s410核115.157.197.60gracal10核 所有的软件安装在/opt/module下,软…...

2678. 老人的数目
给你一个下标从 0 开始的字符串 details 。details 中每个元素都是一位乘客的信息,信息用长度为 15 的字符串表示,表示方式如下: 前十个字符是乘客的手机号码。 接下来的一个字符是乘客的性别。 接下来两个字符是乘客的年龄。 最后两个字符是…...
【刷题-牛客】出栈、入栈的顺序匹配 (代码+动态演示)
【刷题-牛客】出栈、入栈的顺序匹配 (代码动态演示) 文章目录 【刷题-牛客】出栈、入栈的顺序匹配 (代码动态演示) 解题思路 动图演示完整代码多组测试 💗题目描述 💗: 输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个…...
vscode类似GitHub Copilot的插件推荐
由于GitHub Copilot前段时间学生认证的账号掉了很多,某宝激活也是价格翻了几倍,而却,拿来用一天就掉线,可以试试同类免费的插件哦。 例如:TabNine,下载插件后,他会提示你登录,直接登…...

Html -- 文字时钟
Html – 文字时钟 文字时钟,之前在Android上实现了相关效果,闲来无事,弄个网页版的玩玩。。。直接上代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><titl…...

快问快答:关于线上流量卡“归属地随机”几个问题!
在网上办过流量卡的朋友应该都知道,资费虽然便宜,但是归属地却是异地,今天小编就给大家聊一聊关于流量卡归属地的问题。 网上的流量卡都是归属地随机的卡,今天小编以问答的方式给大家普及一下,如果对于归属地有疑问…...

Linux常用命令——clock命令
在线Linux命令查询工具 clock 用于调整 RTC 时间。 补充说明 clock命令用于调整 RTC 时间。 RTC 是电脑内建的硬件时间,执行这项指令可以显示现在时刻,调整硬件时钟的时间,将系统时间设成与硬件时钟之时间一致,或是把系统时间…...
澎湃OS上线:小米告别MIUI,跟小米汽车Say Hi
作者 | Amy 编辑 | 德新 10月17日,雷军发博官宣,「小米将启用全新操作系统,小米澎湃OS(Xiaomi HyperOS)」。 短短几百字的微博,数次提到了「小米汽车」: 小米向人车家全生态迈进,…...

域名不部署SSL证书有什么影响?
SSL证书是保护网站数据传输安全的重要工具,通过加密用户和服务器之间的通信来确保数据的保密性和完整性。然而,如果一个域名没有部署SSL证书,会对网站和用户产生一系列的负面影响。下文中将介绍域名不部署SSL证书的影响,并提供相应…...

Delphi 编程实现拖动排序并输出到文档
介绍:实现拖动排序功能,并将排序后的内容输出到文档中。我们将使用 Delphi 的组件来创建一个界面,其中包括一个 Memo 控件用于输入内容,一个 ListBox 控件用于显示排序后的内容,并且提供按钮来触发排序和输出操作。 代…...

android利用FFmpeg进行视频转换
大致思路:首先安装FFmpeg库到windows电脑上,先测试命令行工具是否可以使用(需要先配置环境),之后再集成到android程序中。 一些命令: 转化为流文件: ffmpeg -i input.mp4 -codec copy -bsf:v …...

Python中不同进制间的转换
Python中不同进制间的转换 一、不同进制在计算机科学、数学和其他领域中具广泛的应用。以下是一些常见的应用:1. 二进制(base-2): 在计算机系统中,数据以二进制形式存储和处理。二进制由0和1组成,是数字电子技术的基础…...
物流监管:智慧仓储数据可视化监控平台
随着市场竞争加剧和市场需求的不断提高,企业亟需更加高效、智能且可靠的仓储物流管理方式,以提升企业的物流效率,减少其输出成本,有效应对市场上的变化和挑战。 图扑自研 HT for Web 产品搭建的 2D 智慧仓储可视化平台,…...

C++对象模型(19)-- 函数语义学:成员函数
1、普通成员函数的调用 1.1 调用方式的转换 为了提高普通成员函数的调用效率,在C中,对普通成员函数的调用,会转换成对全局函数的调用。 假如有下面所示的成员函数: class Test { public:int m_i;int func(int a) {m_i a;retu…...

AI只需26秒,就可以设计一款会走路的机器人
由西北大学、麻省理工学院和佛蒙特大学组成的一支科研团队首次开发出一种可以完全自行设计机器人的 AI 算法。 这一 AI 算法不仅运行速度快,还可在个人计算机上运行,并从头开始设计全新的结构。只需告诉AI“我们想要一个可穿越陆地的机器人”,…...

简单实现spring的set依赖注入
Maven依赖: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0…...
详解)
STM32 HAL库函数——HAL_TIM_Base_Start_IT()详解
以STM32G030C8T6中的HAL_TIM_Base_Start_IT()函数为例,进行解释; 文章目录 一、函数原型和源代码二、函数用法详解:2.1 参数2.1.1 TIM_HandleTypeDef结构体详解 2.2 使用场景:2.3 使用方法: 三、函数使用示例ÿ…...
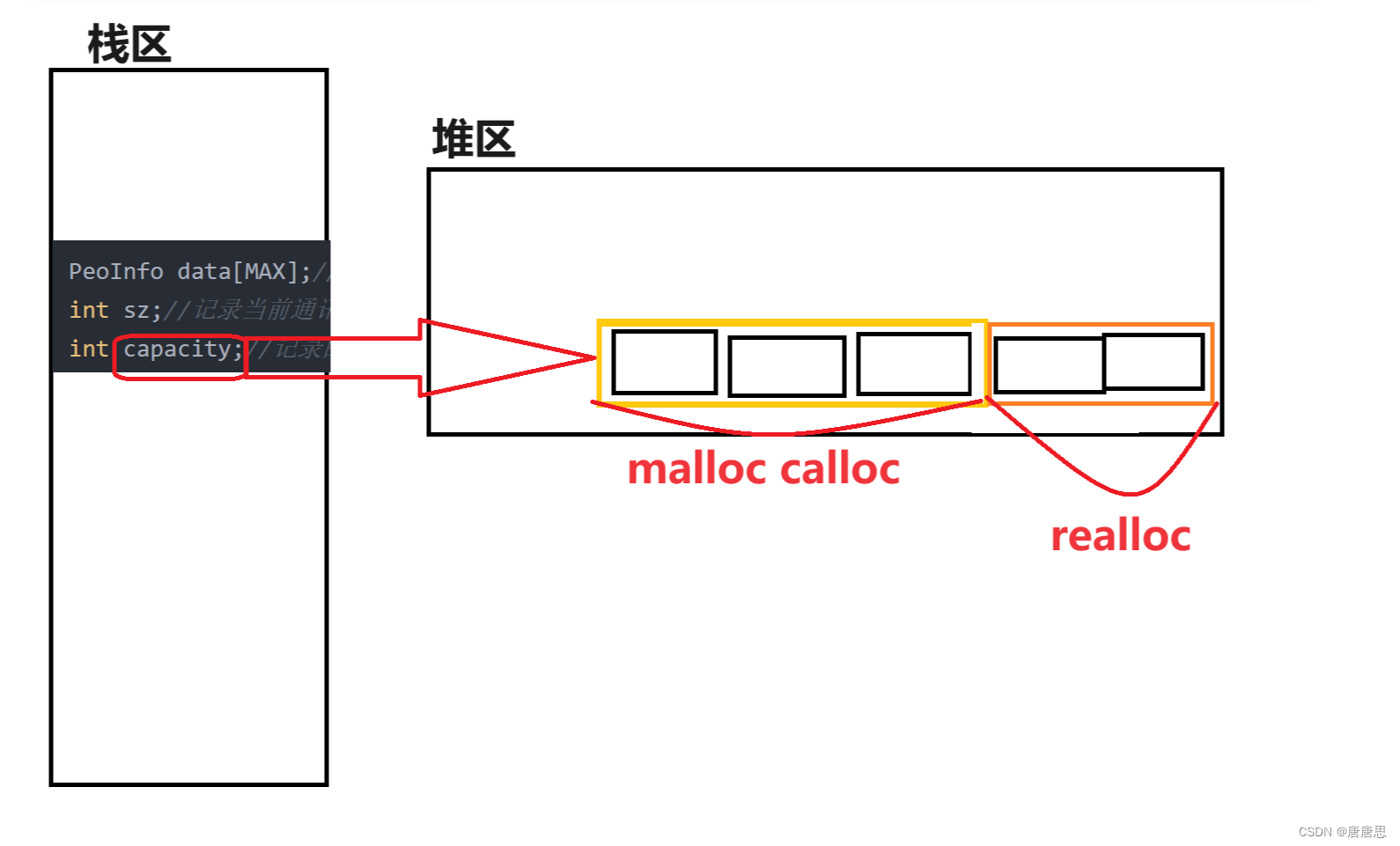
C语言之通讯录的实现篇优化版
目录 动态内存管理 通讯录声明 静态版本 动态版本 初始化通讯录 静态版本 动态版本 Add增加通讯录 静态版本 动态版本 Checkcapacity增容 DestroyContact释放动态空间 文件操作 SaveContact保存信息到文件中 初始化通讯录 旧版本 文件版本 LoadContact加载…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

MCP和Function Calling
MCP MCP(Model Context Protocol,模型上下文协议) ,2024年11月底,由 Anthropic 推出的一种开放标准,旨在统一大模型与外部数据源和工具之间的通信协议。MCP 的主要目的在于解决当前 AI 模型因数据孤岛限制而…...

视觉slam--框架
视觉里程计的框架 传感器 VO--front end VO的缺点 后端--back end 后端对什么数据进行优化 利用什么数据进行优化的 后端是怎么进行优化的 回环检测 建图 建图是指构建地图的过程。 构建的地图是点云地图还是什么信息的地图? 建图并没有一个固定的形式和算法…...

Redis——Cluster配置
目录 分片 一、分片的本质与核心价值 二、分片实现方案对比 三、分片算法详解 1. 范围分片(顺序分片) 2. 哈希分片 3. 虚拟槽分片(Redis Cluster 方案) 四、Redis Cluster 分片实践要点 五、经典问题解析 C…...

网络安全问题及对策研究
摘 要 网络安全问题一直是近年来社会乃至全世界十分关注的重要性问题,网络关乎着我们的生活,政治,经济等多个方面,致力解决网络安全问题以及给出行之有效的安全策略是网络安全领域的一大目标。 本论文简述了课题的开发背景&…...

Ubantu-Docker配置最新镜像源250605
尝试其他镜像加速器 阿里云镜像加速器:登录阿里云,进入容器镜像服务获取专属加速器地址。毫秒镜像:https://docker.1ms.run。DockerHub镜像加速器:https://docker.xuanyuan.me。Docker Hub 镜像加速服务:https://dock…...
