[CSP-S 2023] 种树 —— 二分+前缀和
This way
题意:
一开始以为是水题,敲了一个二分+贪心检查的代码,20分。发现从根往某个节点x走的时候,一路走来的子树上的节点到已栽树的节点的距离会变短,那么并不能按照初始情况贪心。
于是就想着检查时候用线段树,存的是(每个节点最晚开始时间-它距离最近栽树的点的距离)往后就将这个称为ddl。每一步都往当前最小值的位置走,每走一步,将当前这一步的子树区间+1,如此往复。当走到一个点发现已经走的步数>这个点最晚开始时间时候就是not。但是代码过于繁杂,最终放弃了这样思路,而且常数可能会比较大,最终如果TLE了血亏。
首先这道题的答案满足二分的性质,考虑使用二分。二分出来结束时间的时候,我们可以求出每个点的最晚到达时间,首先分c>=0和c<0两种情况。对于c<0的时候又要分三种情况。其实就是等差数列求和公式,但是注意会爆longlong,所以转乘为除。我这里使用二分去找答案,当然直接算好像也行?
发现其实每个点的ddl就是它子树的ddl最小值,也就是每个点的ddl可视为子树中最小ddl-当前点到ddl最小的节点的距离,例如:
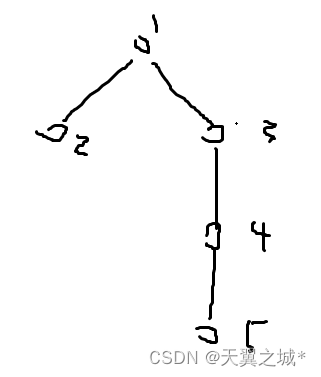
假设点1的最晚开始时间是第10天,点2是第3天,点3是第50天,点4是第90天,点5是第4天。那么转换过来,其实它们真实的ddl如下:
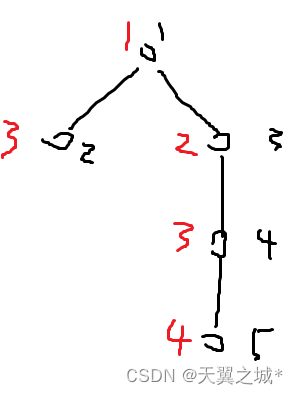
这个时候我们只需要将所有真·ddl存到桶里面,再做一个前缀和,记为num[i]。若i<num[i],则表示你走了i步,但是有超过i个点的ddl在i步之内(我们在上图处理完之后,所有链上的ddl必然是递增的也就是如果点x需要走10步,那father[x]最大为9,father[father[x]]最大为8,也就是为x做铺垫),那么表示无法在i步内满足num[i]个点的ddl。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
ll a[N],b[N],c[N],en[N],e,shou,mo;
int n,x,y,dep[N],u,tim,num[N],t[N];
vector<int>vec[N];
bool vis[N];
#define pii pair<int,int>
vector<pii>day;
int dfs(int x,int fa){for(int ne:vec[x]){if(ne==fa)continue;t[x]=min(t[x],dfs(ne,x)-1);}num[t[x]]++;return t[x];
}
bool check(ll d){day.clear();memset(num,0,sizeof num);for(int i=1;i<=n;i++){ll l=1,r=min(1ll*n,d);t[i]=-1;while(l<=r){ll x=l+r>>1;if(c[i]>=0){if((a[i]*2ll+d-x)/(d-x+1)<=2*b[i]+(x+d)*c[i])t[i]=x,l=x+1;else r=x-1;}else{c[i]=-c[i];if(en[i]<=x){if(a[i]<=d-x+1)t[i]=x,l=x+1;else r=x-1;}else if(en[i]<=d){e=en[i]-1;shou=b[i]-x*c[i],mo=b[i]-e*c[i];if((2*a[i]-2*(d-e)+e-x)/(e-x+1)<=(shou+mo))t[i]=x,l=x+1;else r=x-1;}else{ll shou=b[i]-x*c[i],mo=b[i]-d*c[i];if((2*a[i]+d-x)/(d-x+1)<=(shou+mo))t[i]=x,l=x+1;else r=x-1;}c[i]=-c[i];}}if(t[i]-dep[i]<=0)return 0;}dfs(1,0);for(int i=1;i<=n;i++){num[i]+=num[i-1];if(num[i]>i)return 0;}return 1;
}
int main()
{ll l=n,r=0,ans=-1;scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%lld%lld%lld",&a[i],&b[i],&c[i]);r=max(r,a[i]);if(c[i]<0)en[i]=(b[i]-c[i]-1)/(-c[i]);}r=min(r,1000000000ll);for(int i=1;i<n;i++){scanf("%d%d",&x,&y);vec[x].push_back(y),vec[y].push_back(x);}while(l<=r){ll mid=l+r>>1;if(check(mid))r=mid-1,ans=mid;else l=mid+1;}printf("%lld\n",ans);return 0;
}相关文章:

[CSP-S 2023] 种树 —— 二分+前缀和
This way 题意: 一开始以为是水题,敲了一个二分贪心检查的代码,20分。发现从根往某个节点x走的时候,一路走来的子树上的节点到已栽树的节点的距离会变短,那么并不能按照初始情况贪心。 于是就想着检查时候用线段树…...

【LeetCode周赛】LeetCode第368场周赛
目录 元素和最小的山形三元组 I元素和最小的山形三元组 II合法分组的最少组数 元素和最小的山形三元组 I 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个山形三元组 : i < j < k nums[i] &l…...
【智慧工地源码】基于AI视觉技术赋能智慧工地
伴随着技术的不断发展,信息化手段、移动技术、智能穿戴及工具在工程施工阶段的应用不断提升,智慧工地概念应运而生,庞大的建设规模催生着智慧工地的探索和研发。 建筑施工具有周期长、环境复杂、工序繁杂、人员流动性大等特点,所以…...

云服务器搭建Hadoop分布式
文章目录 1.服务器配置2.Java环境3. 安装Hadoop4. 集群配置5. 编写集群的启动脚本 1.服务器配置 服务器主机名配置115.157.197.82s110核115.157.197.84s210核115.157.197.109s310核115.157.197.31s410核115.157.197.60gracal10核 所有的软件安装在/opt/module下,软…...

2678. 老人的数目
给你一个下标从 0 开始的字符串 details 。details 中每个元素都是一位乘客的信息,信息用长度为 15 的字符串表示,表示方式如下: 前十个字符是乘客的手机号码。 接下来的一个字符是乘客的性别。 接下来两个字符是乘客的年龄。 最后两个字符是…...
【刷题-牛客】出栈、入栈的顺序匹配 (代码+动态演示)
【刷题-牛客】出栈、入栈的顺序匹配 (代码动态演示) 文章目录 【刷题-牛客】出栈、入栈的顺序匹配 (代码动态演示) 解题思路 动图演示完整代码多组测试 💗题目描述 💗: 输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个…...
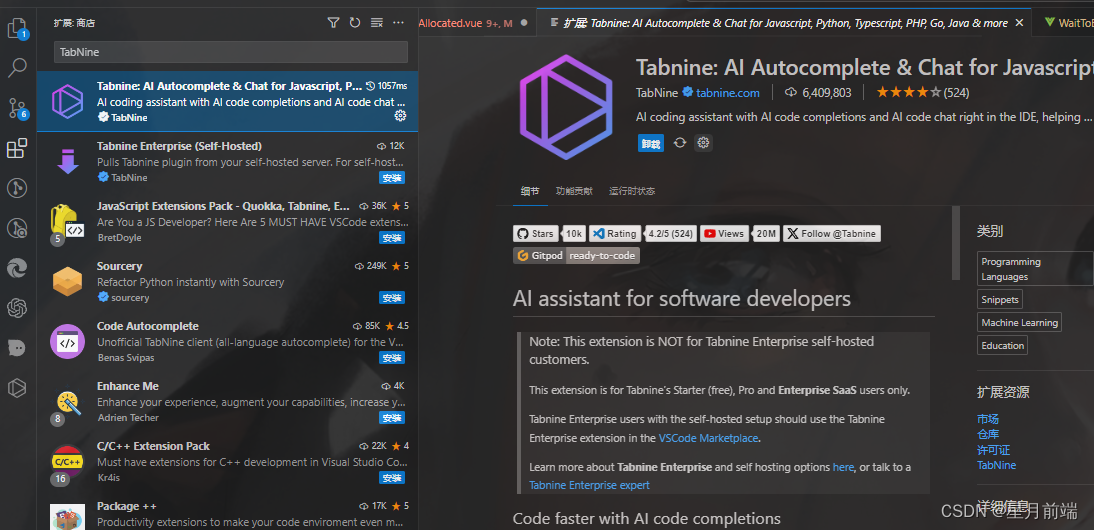
vscode类似GitHub Copilot的插件推荐
由于GitHub Copilot前段时间学生认证的账号掉了很多,某宝激活也是价格翻了几倍,而却,拿来用一天就掉线,可以试试同类免费的插件哦。 例如:TabNine,下载插件后,他会提示你登录,直接登…...

Html -- 文字时钟
Html – 文字时钟 文字时钟,之前在Android上实现了相关效果,闲来无事,弄个网页版的玩玩。。。直接上代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><titl…...

快问快答:关于线上流量卡“归属地随机”几个问题!
在网上办过流量卡的朋友应该都知道,资费虽然便宜,但是归属地却是异地,今天小编就给大家聊一聊关于流量卡归属地的问题。 网上的流量卡都是归属地随机的卡,今天小编以问答的方式给大家普及一下,如果对于归属地有疑问…...

Linux常用命令——clock命令
在线Linux命令查询工具 clock 用于调整 RTC 时间。 补充说明 clock命令用于调整 RTC 时间。 RTC 是电脑内建的硬件时间,执行这项指令可以显示现在时刻,调整硬件时钟的时间,将系统时间设成与硬件时钟之时间一致,或是把系统时间…...
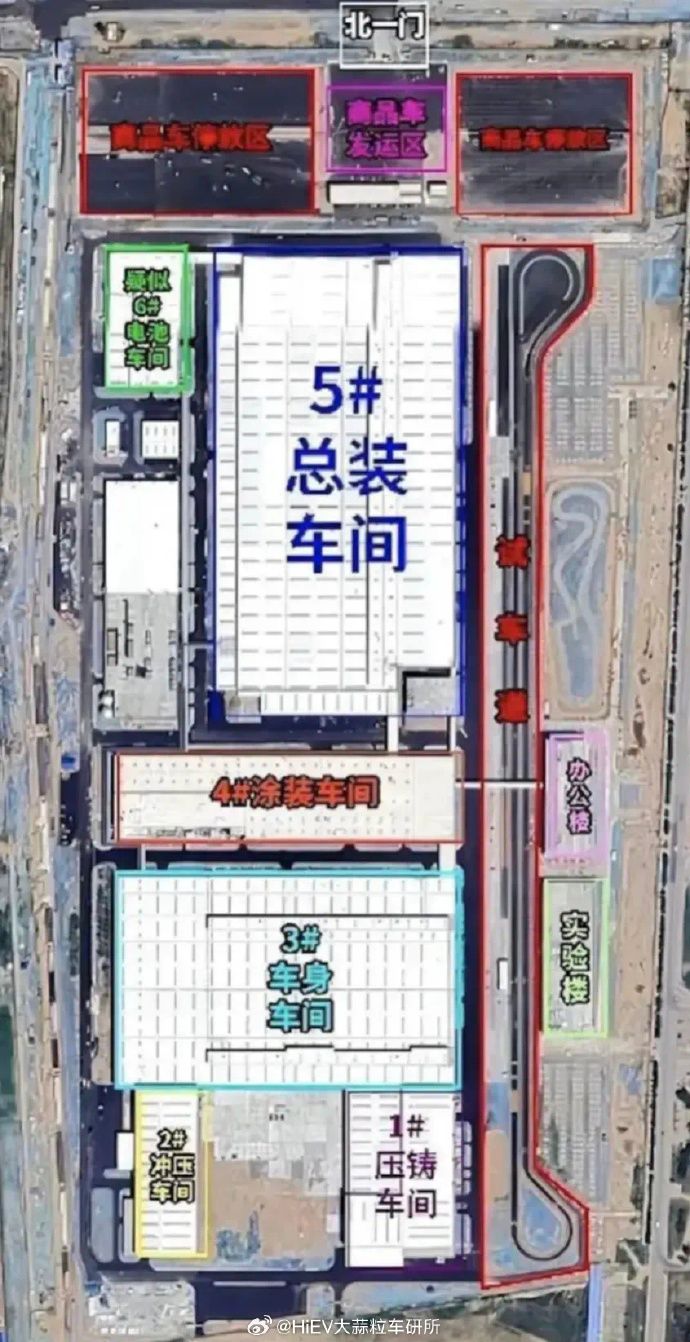
澎湃OS上线:小米告别MIUI,跟小米汽车Say Hi
作者 | Amy 编辑 | 德新 10月17日,雷军发博官宣,「小米将启用全新操作系统,小米澎湃OS(Xiaomi HyperOS)」。 短短几百字的微博,数次提到了「小米汽车」: 小米向人车家全生态迈进,…...

域名不部署SSL证书有什么影响?
SSL证书是保护网站数据传输安全的重要工具,通过加密用户和服务器之间的通信来确保数据的保密性和完整性。然而,如果一个域名没有部署SSL证书,会对网站和用户产生一系列的负面影响。下文中将介绍域名不部署SSL证书的影响,并提供相应…...

Delphi 编程实现拖动排序并输出到文档
介绍:实现拖动排序功能,并将排序后的内容输出到文档中。我们将使用 Delphi 的组件来创建一个界面,其中包括一个 Memo 控件用于输入内容,一个 ListBox 控件用于显示排序后的内容,并且提供按钮来触发排序和输出操作。 代…...

android利用FFmpeg进行视频转换
大致思路:首先安装FFmpeg库到windows电脑上,先测试命令行工具是否可以使用(需要先配置环境),之后再集成到android程序中。 一些命令: 转化为流文件: ffmpeg -i input.mp4 -codec copy -bsf:v …...

Python中不同进制间的转换
Python中不同进制间的转换 一、不同进制在计算机科学、数学和其他领域中具广泛的应用。以下是一些常见的应用:1. 二进制(base-2): 在计算机系统中,数据以二进制形式存储和处理。二进制由0和1组成,是数字电子技术的基础…...
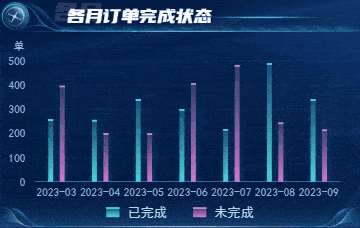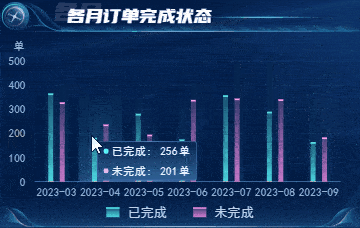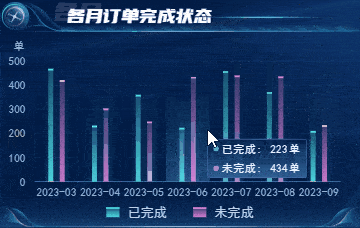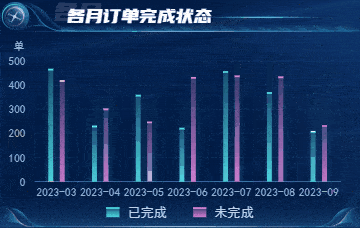
物流监管:智慧仓储数据可视化监控平台
随着市场竞争加剧和市场需求的不断提高,企业亟需更加高效、智能且可靠的仓储物流管理方式,以提升企业的物流效率,减少其输出成本,有效应对市场上的变化和挑战。 图扑自研 HT for Web 产品搭建的 2D 智慧仓储可视化平台,…...

C++对象模型(19)-- 函数语义学:成员函数
1、普通成员函数的调用 1.1 调用方式的转换 为了提高普通成员函数的调用效率,在C中,对普通成员函数的调用,会转换成对全局函数的调用。 假如有下面所示的成员函数: class Test { public:int m_i;int func(int a) {m_i a;retu…...

AI只需26秒,就可以设计一款会走路的机器人
由西北大学、麻省理工学院和佛蒙特大学组成的一支科研团队首次开发出一种可以完全自行设计机器人的 AI 算法。 这一 AI 算法不仅运行速度快,还可在个人计算机上运行,并从头开始设计全新的结构。只需告诉AI“我们想要一个可穿越陆地的机器人”,…...

简单实现spring的set依赖注入
Maven依赖: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0…...
详解)
STM32 HAL库函数——HAL_TIM_Base_Start_IT()详解
以STM32G030C8T6中的HAL_TIM_Base_Start_IT()函数为例,进行解释; 文章目录 一、函数原型和源代码二、函数用法详解:2.1 参数2.1.1 TIM_HandleTypeDef结构体详解 2.2 使用场景:2.3 使用方法: 三、函数使用示例ÿ…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
