算法进修Day-36
算法进修Day-36
71. 简化路径
难度:中等
题目要求:
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 '/' 开头),请你将其转化为更加简洁的规范路径。
在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (..) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,'//')都被视为单个斜杠 '/' 。 对于此问题,任何其他格式的点(例如,'...')均被视为文件/目录名称。
请注意,返回的 规范路径 必须遵循下述格式:
- 始终以斜杠
'/'开头。 - 两个目录名之间必须只有一个斜杠
'/'。 - 最后一个目录名(如果存在)不能 以
'/'结尾。 - 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含
'.'或'..')。
返回简化后得到的 规范路径 。
示例1
输入:path = “/home/”
输出:“/home”
示例2
输入:path = “/…/”
输出:“/”
示例3
输入:path = “/home//foo/”
输出:“/home/foo”
示例4
输入:path = “/a/./b/…/…/c/”
输出:“/c”
题解
提供两条API内容解释:
- System.IO.Path.TrimEndingDirectorySeparator(String)
- 剪裁一个超出指定路径根目录的尾随目录分隔符。
- System.IO.Path.GetFullPath(String)
- 返回指定路径字符串的绝对路径。
想法代码
class Solution
{public static void Main(String[] args){string path = "/../";Solution solution = new Solution();string res = solution.SimplifyPath(path);Console.WriteLine(res);}public string SimplifyPath(string path){return Path.TrimEndingDirectorySeparator(Path.GetFullPath(path));}
}
72. 编辑距离
难度:困难
题目要求
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例1
输入:word1 = “horse”, word2 = “ros”
输出:3
示例2
输入:word1 = “intention”, word2 = “execution”
输出:5
题解
利用动态规划,用 m m m 和 n n n 分别表示字符串 w o r d 1 word_1 word1 和 w o r d 2 word_2 word2 的长度,对于满足 1 ≤ i ≤ m 1\leq i\leq m 1≤i≤m 和 1 ≤ j ≤ n 1\leq j\leq n 1≤j≤n 的每个下标对 ( i , j ) (i,j) (i,j),需要分别计算将 w o r d 1 word_1 word1 的前 i i i 个字符转换成 w o r d 2 word_2 word2 的前 j j j 个字符的最小操作数
创建 ( m + 1 ) ∗ ( n + 1 ) (m+1)*(n+1) (m+1)∗(n+1) 的二维数组 d p dp dp,其中 d p [ i ] [ j ] dp[i][j] dp[i][j] 为将 w o r d 1 word_1 word1 的前 i i i 个字符转换成 w o r d 2 word_2 word2 的前 j j j 个字符的最小操作数
如果 i = 0 i=0 i=0,则对于任意 j j j,需要将 w o r d 2 word_2 word2 的前 j j j 个字符全部删除,最少操作数是 j j j,如果 j = 0 j=0 j=0,则对于任意 i i i,需要将 w o r d 1 word_1 word1 的前 i i i 个字符全部删除,最少操作数是 i i i,因此动态规划边界为:对于任意 0 ≤ j ≤ n , d p [ 0 ] [ j ] = j 0\leq j\leq n, dp[0][j]=j 0≤j≤n,dp[0][j]=j,对于任意 0 ≤ i ≤ m , d p [ i ] [ 0 ] = i 0\leq i\leq m, dp[i][0]=i 0≤i≤m,dp[i][0]=i,当然, d p [ 0 ] [ 0 ] = 0 dp[0][0]=0 dp[0][0]=0
当 1 ≤ i ≤ m 1\leq i\leq m 1≤i≤m 且 1 ≤ j ≤ n 1\leq j\leq n 1≤j≤n 时,让 c 1 = w o r d 1 [ i − 1 ] , c 2 = w o r d 2 [ j − 1 ] c_1=word_1[i-1], c_2=word_2[j-1] c1=word1[i−1],c2=word2[j−1],总共分为两种情况
- 当 c 1 = c 2 c_1=c_2 c1=c2,将 c 1 c_1 c1 和 c 2 c_2 c2 成为公共字符,将 w o r d 1 word_1 word1 的前 i − 1 i-1 i−1 个字符的最小操作数是 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1],所以 d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] dp[i][j]=dp[i-1][j-1] dp[i][j]=dp[i−1][j−1]
- 当 c 1 ≠ c 2 c_1\neq c_2 c1=c2 时,计算将 w o r d 1 word_1 word1 的前 i i i 个字符串转换成 w o r d 2 word_2 word2 的前 j j j 个字符的最少操作数时需要考虑三种可能的操作,取其中的最小操作数作为 d p [ i ] [ j ] dp[i][j] dp[i][j]
- 第一种操作是插入字符 c 1 c_1 c1,操作之前的最少操作数是 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j],操作之后的最少操作数是 d p [ i − 1 ] [ j ] + 1 dp[i-1][j]+1 dp[i−1][j]+1
- 第二种操作是删除字符 c 2 c_2 c2,操作之前的最少操作数是 d p [ i ] [ j − 1 ] dp[i][j-1] dp[i][j−1],操作之后的最少操作数是 d p [ i ] [ j − 1 ] + 1 dp[i][j-1]+1 dp[i][j−1]+1
- 第三种操作是将字符 c 1 c_1 c1 替换为 c 2 c_2 c2,操作之前的最少操作数是 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1],操作之后的最少操作数是 d p [ i − 1 ] [ j − 1 ] + 1 dp[i-1][j-1]+1 dp[i−1][j−1]+1
动态规划转移方程如下
d p [ i ] [ j ] = { d p [ i − 1 ] [ j − 1 ] , word1[i-1]=word2[j-1] m i n ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j − 1 ] ) + 1 , word1[i-1]!=word2[j-1] dp[i][j]=\begin{cases} dp[i-1][j-1],&\text{word1[i-1]=word2[j-1]}\\min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1,&\text{word1[i-1]!=word2[j-1] } \end{cases} dp[i][j]={dp[i−1][j−1],min(dp[i−1][j],dp[i][j−1],dp[i−1][j−1])+1,word1[i-1]=word2[j-1]word1[i-1]!=word2[j-1] 根据动态规划转移方程,计算 d p [ i ] [ j ] dp[i][j] dp[i][j] 的顺序为从小到大遍历每个 i i i,对于每个 i i i 从小到大遍历每个 j j j。最后 d p [ m ] [ n ] dp[m][n] dp[m][n] 即为最少操作数
想法代码
public class Solution
{public static void Main(string[] args){Solution solution = new Solution();string word1 = "horse";string word2 = "ros";Console.WriteLine(solution.MinDistance(word1,word2));}public int MinDistance(string word1, string word2){int m = word1.Length, n = word2.Length;int[][] dp = new int[m + 1][];for (int i = 0; i <= m; i++){dp[i] = new int[n + 1];}for (int j = 1; j <= n; j++){dp[0][j] = j;}for (int i = 1; i <= m; i++){dp[i][0] = i;}for (int i = 1; i <= m; i++){char c1 = word1[i - 1];for (int j = 1; j <= n; j++){char c2 = word2[j - 1];if (c1 == c2){dp[i][j] = dp[i - 1][j - 1];}else{dp[i][j] = Math.Min(Math.Min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;}}}return dp[m][n];}
}
相关文章:

算法进修Day-36
算法进修Day-36 71. 简化路径 难度:中等 题目要求: 给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 / 开头),请你将其转化为更加简洁的规范路径。 在 Unix 风格的文件系统中&am…...

postman自动化运行接口测试用例
做过接口测试的人,应该都知道postman ,我们在日常的时候都可以利用postman做接口测试,我们可以把接口的case保存下来在collection里面,那么可能会有这样的需求,我们怎么把collection的用例放到jenkins中定时执行呢&…...
【Linux】Linux环境搭建
Linux环境搭建 前言Linux 环境的搭建方式一、Linux环境搭载购买云服务器 二、 使用 XShell 远程登陆到 Linux关于 Linux 桌面下载安装 XShell查看 Linux 主机 ip使用 XShell 登陆主机XShell 下的复制粘贴 前言 Linux 环境的搭建方式 主要有三种 直接安装在 物理机 上. 但是由…...

k8s day07
昨日内容回顾: - 污点: 影响Pod调度,污点是作用在worker节点上。语法格式: KEY[VALUE]:EFFECT 有三种污点。 EFFECT: - NoSchedule: 已经调度到当前节点的Pod不驱逐,并且不在接…...

压力大,休息日都没有,更别说年休假了
我一周要工作六天,每天至少十小时,连个休息日都没有。哪来的年休假?...

人手一个助理,三句话让AI替我们上班
目录 前言 从大模型上长出来的 AI 原生应用,才是关键 而这看起来只是一个小小的办公沟通场景,却是大模型重构的一个非常典型的场景。背后考验的也是大模型的综合能力应用 这种从AI原生角度进行的重构,离不开大模型的理解、生成、逻辑、记…...

【Eclipse Maven Tycho】如何通过maven执行eclipse application
通过maven执行eclipse application 前言命令行下运行通过maven tycho运行 前言 eclipse其实不只是一个桌面(GUI)程序,他还可以是一个命令行程序。如果你的产品或软件是基于eclipse开发的,并且他没有UI相关的功能,那么…...

(一)docker:建立oracle数据库
前言,整个安装过程主要根据docker-images/OracleDatabase/SingleInstance /README.md ,里边对如何制作容器讲的比较清楚,唯一问题就是都是英文,可以使用谷歌浏览器自动翻译成中文,自己再对照英文相互参照来制作提前准备…...
在配置文件“tsconfig.json”中找不到任何输入。指定的 “include“ 路径为“[“**/*“]”,“exclude“ 路径为[]
在vscode中项目下的tsconfig.json莫名报错 解决办法 在目录中随便创建一个后缀为.ts的文件 便不再报错...

java编译时指定classpath
说明 Java编译时可以通过选项--class-path <path>,或者 -classpath <path>,或者-cp <path>来指定查找用户类文件、注释程序处理程序、或者源文件的位置。这个设置覆盖CLASSPATH环境变量的设置。如果没有设置-sourcepath,那…...
分享一下抽奖活动小程序怎么做
在当今数字化时代,抽奖活动小程序已成为一种高效、创新的营销方式。它不仅能够吸引用户的注意力,提高品牌知名度,还能促进用户参与度,增强用户对品牌的忠诚度。本文将详细介绍如何制作一个成功的抽奖活动小程序,以及它…...

同为科技(TOWE)工业级多位USB快充桌面PDU插座
如今,许多便捷式、轻薄化电子设备越来越多,很多设备上预留的端口越来越少,甚至很多款笔记本电脑只预留了一个单一的Type-C接口。这样做虽然在体验感、美观度和轻薄尺寸的优势显而易见,然而也存在接口不足的明显弊端。USB快充插排产…...

testt
wd wwwwwwwwwwwwww qdwqdwqd...
Git Bash(一)Windows下安装及使用
目录 一、简介1.1 什么是Git?1.2 Git 的主要特点1.3 什么是 Git Bash? 二、下载三、安装3.1 同意协议3.2 选择安装位置3.3 其他配置(【Next】 即可)3.4 安装完毕3.5 打开 Git Bash 官网地址: https://www.git-scm.com/…...

软考公告 | 关于2023年下半年软考批次安排
按照《2023年下半年计算机技术与软件专业技术资格(水平)考试有关工作调整的通告》,自2023年下半年起,计算机软件资格考试方式均由纸笔考试改革为计算机化考试。 为进一步提升考试服务质量和水平, 便利考生考试, 减少考生参加考试…...
react 中ref 属性的三种写法
目录 1. 字符串 ref 2.dom节点上使用回调函数ref 3.React.createRef() 1. 字符串 ref 最早的ref用法。(由于效率问题,现在官方不推荐使用这种写法。) 1.dom节点上使用,通过this.refs.xxxx来引用真实的dom节点 <input ref&q…...

v4l2-ioctl.c的一些学习和整理
可以发现,这个宏用的很好,简洁易扩展,自己写代码可以学习下 #define IOCTL_INFO(_ioctl, _func, _debug, _flags) \[_IOC_NR(_ioctl)] { \.ioctl _ioctl, \.flags _flags, \.name #_ioctl, \.func _func, \.debug _…...
Python实战小项目分享
Python实战小项目包括网络爬虫、数据分析和可视化、文本处理、图像处理、聊天机器人、任务管理工具、游戏开发和网络服务器等。这些项目提供了实际应用场景和问题解决思路,可以选择感兴趣的项目进行实践,加深对Python编程的理解和掌握。在实践过程中&…...
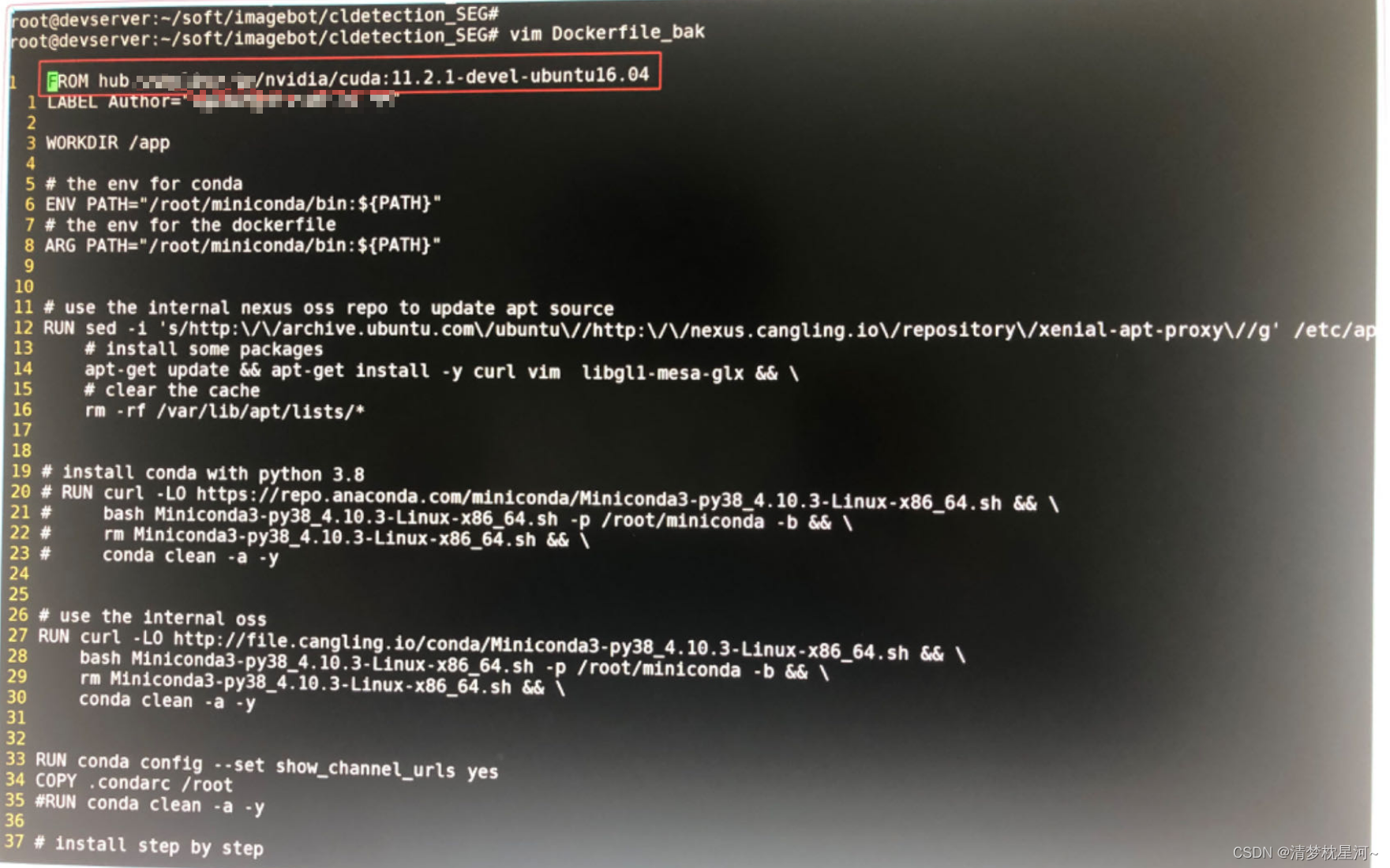
使用Dockerfile生成docker镜像和容器的方法记录
一、相关介绍 Docker 是一个开源的容器化平台,其中的主要概念是容器和镜像。 容器是 Docker 的运行实例。 它是一个独立并可执行的软件包,包含了应用程序及其依赖的所有组件(如代码、运行时环境、系统工具、库文件等)。容器可以在…...

美国亚马逊UL60335认证怎么办理,费用是多少
UL60335认证是由美国安全实验室(UnderwritersLaboratories)颁发的,它对各类家用电器进行严格的测试和认证,确保其在正常使用情况下不会给消费者带来任何伤害。 本文将从不同的角度来叙述亚马逊UL60335认证的重要性和成败因素。 1.…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
