Leetcode第 368 场周赛
元素和最小的山形三元组 II
预处理前缀和后缀最小值,记为pre[i]和sa[i]
对于当前编号i,如果前面的最小值和后面的最大值都小于nums[i],则记录ans[i] = nums[i]+pre[i-1]+sa[i+1]
结果输出最小的ans[i]即可。
合法分组的最少组数
统计每一个数字出现的次数。将每一个数字分为大小为 d d d或 d + 1 d+1 d+1的组,令 d d d尽可能大。
d d d不满足单调性,不好二分。思路时直接暴力。
计最小出现次数为 m n mn mn,出现过的数字个数为 c n t cnt cnt,显然有 m n ∗ c n t ≤ n u m s . l e n g t h mn*cnt \le nums.length mn∗cnt≤nums.length
而显然有 d + 1 ≤ m n d+1 \le mn d+1≤mn,因此直接枚举d
对于某个数字i,其出现次数为 t o t i tot_i toti,若 d d d成立则需要满足存在x令 x d ≤ t o t i ≤ x ( d + 1 ) xd \le tot_i \le x(d+1) xd≤toti≤x(d+1)
令 x = t o t i / d x = tot_i/d x=toti/d,即以 d d d为标准将 t o t i tot_i toti分为x组,此时还剩 t o t i % d tot_i\%d toti%d个元素,每一组中最多可以容纳 d + 1 d+1 d+1个元素,最多可以容纳x个元素,使x组的个数都变为%d+1%。因此只要满足 t o t i % d ≤ x tot_i\%d \le x toti%d≤x即 t o t i % d ≤ t o t i / d tot_i\%d \le tot_i/d toti%d≤toti/d,则对数字 i i i而言 d d d是合法的分组。
已知d,数字i的分组个数为 t o t i + d m n + 1 \frac{tot_i+d}{mn+1} mn+1toti+d。 x x x需要取最小值满足 x d ≤ t o t i ≤ x ( d + 1 ) xd \le tot_i \le x(d+1) xd≤toti≤x(d+1),有 ⌈ t o t i / ( d + 1 ) ⌉ ≤ x \lceil tot_i/(d+1)\rceil \le x ⌈toti/(d+1)⌉≤x,因此取 x = ⌈ t o t i d + 1 ⌉ x =\lceil \frac{tot_i}{d+1}\rceil x=⌈d+1toti⌉
枚举 d d d,计算分组个数,求分组最小值即可,复杂度为 O ( m n ∗ c n t ) O(mn*cnt) O(mn∗cnt)
得到 K 个半回文串的最少修改次数
数据只有200,想法是纯暴力
令 M i n T i m e s [ i ] [ j ] MinTimes[i][j] MinTimes[i][j]为子串 s t r i j str_{ij} strij变成半回文串最少的次数,暴力计算,复杂度为 O ( n 4 ) O(n^4) O(n4)
令dp[i][j]为以 s t r i str_i stri为结尾时分为 j j j段最少的操作次数
d p [ i ] [ j ] = min d p [ z ] [ j − 1 ] + M i n T i m e s [ z + 1 ] [ i ] dp[i][j] = \min dp[z][j-1]+MinTimes[z+1][i] dp[i][j]=mindp[z][j−1]+MinTimes[z+1][i]
总复杂度 O ( n 4 ) O(n^4) O(n4)
计算MinTimes时可以将一个n优化成 n \sqrt n n甚至预处理成 lg n \lg n lgn,但是 O ( n 4 ) O(n^4) O(n4)也能过就是了,大概是数据比较弱吧
class Solution {
public:int MinTimes[210][210];int dp[210][210];int calTimes(string &s,int l,int r){int ret = (1<<30);int len = r-l+1;while(--len){if((r-l+1)%len)continue;int ans = 0;for(int i=0;i<len;++i){string t1;for(int j=l+i;j<=r;j+=len)t1 += s[j];for(int c=0;c<t1.size()/2;++c)if(t1[c]!=t1[t1.size()-1-c])ans++;}ret = min(ret,ans);}return ret;}int minimumChanges(string s, int k) {memset(dp,0x3f,sizeof(dp));dp[0][0] = 0;int l = s.size(); for(int i=0;i<l;++i){for(int j=i+1;j<l;++j){MinTimes[i][j] = calTimes(s,i,j);}MinTimes[i][i] = (1<<30);}for(int i=0;i<l;++i){for(int j=0;j<=i;++j){for(int z=1;z<=k;++z){dp[i+1][z] = min(dp[i+1][z],dp[j][z-1]+MinTimes[j][i]);}}}return dp[l][k];}
};
相关文章:

Leetcode第 368 场周赛
元素和最小的山形三元组 II 预处理前缀和后缀最小值,记为pre[i]和sa[i] 对于当前编号i,如果前面的最小值和后面的最大值都小于nums[i],则记录ans[i] nums[i]pre[i-1]sa[i1] 结果输出最小的ans[i]即可。 合法分组的最少组数 统计每一个数字出现的次数。将每一个数…...
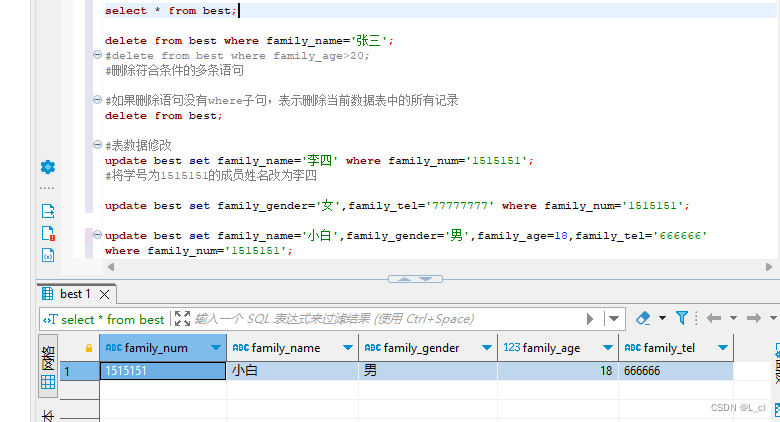
Mysql数据库 3.SQL语言 DML数据操纵语言 增删改
DML语句:用于完成对数据表中数据的插入、删除、修改操作 一.表数据插入 插入数据语法: 步骤例: 1.声明数据库:use 数据库名; 2.删除操作:drop table if exists 表名; 3.创建数据库中的表:create table 表…...

Java中,如何去掉字符串中前面所有的0
大家好,我是三叔,这期主要给大家分享下在开发中使用的字符串的一些常见方法。 例如:00000000110,现在需要去掉前面所有补的0,得到110,相信大家在开发中肯定有遇到过类似的开发需求,如何做&…...

数组能开空间大小
奈何辰星无可奈_leetcode,中等难度,算法-CSDN博客 这个博客介绍的很好,可以参考下...

Python 数据类 - dataclass 的作用与不足
https://docs.python.org/zh-cn/3/library/dataclasses.html https://peps.python.org/pep-0526/ https://peps.python.org/pep-0557/ dataclass 简单示例 from dataclasses import dataclassdataclass class User:name: strage: intif __name__ __main__:response_json {na…...

【C++初阶】类与对象(一)
目录 1、初识面向对象思想2、类 struct2.1 C中的struct及使用 3、类 class3.1 类的定义3.2 类的访问限定符3.2.1 访问限定符是什么3.2.2 访问限定符的使用3.2.3 访问限定符的使用规范3.2.4 访问限定符与封装 3.3 类做声明和定义分离3.3.1 声明和定义分离3.3.2 在函数声明的地方…...

thinkPHP框架详解+部署
目录 什么是ThinkPHP: ThinkPHP的主要特性: 什么是ThinkPHP: ThinkPHP是一个快速、兼容而且简单的轻量级国产PHP开发框架,诞生于2006年初,由国内的技术爱好者创建,遵循Apache2开源协议发布,是为了敏捷WEB应用开发和…...

Java拦截器(Interceptor)和过滤器(Filter)实例详解
一、Java过滤器和拦截器 1.1、过滤器(Filter) Filter过滤器,是Servlet(Server Applet)技术中的技术,开发人员可以通过Filter技术,管理web资源,可以对指定的一些行为进行拦截,例如URL级别的权限…...
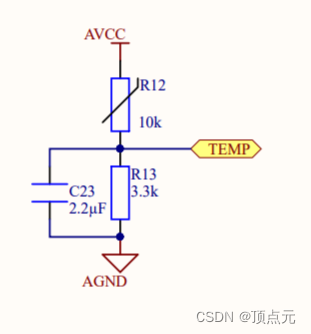
通过热敏电阻计算温度(二)---ODrive实现分析
文章目录 通过热敏电阻计算温度(二)---ODrive实现分析测量原理图计算分析计算拟合的多项式系数根据多项式方程计算温度的函数温度计算调用函数 通过热敏电阻计算温度(二)—ODrive实现分析 ODrive计算热敏电阻的温度采用的时B值的…...

基于typescript+express实现一个简单的接口权限验证
package.json "scripts": {"start": "nodemon src/main.ts","start:a": "nodemon src/a.ts","build": "tsc","build:dev": "tsc src/main.ts"}, express服务器文件 import * as…...

yolov7改进优化之蒸馏(二)
续yolov7改进优化之蒸馏(一)-CSDN博客 上一篇已经基本写出来yolov7/v5蒸馏的整个过程,不过要真的训起来我们还需要进行一些修改。 Model修改 蒸馏需要对teacher和student网络的特征层进行loss计算,因此我们forward时要能够返回需…...
的历史)
生产与作业管理(POM)的历史
1800年,惠特尼:零件标准化、质量管理。 1881年,泰勒:人员选拔、计划和时程安排、动作研究。管理与劳动分开。 - 使雇员与工作相适应。 - 提供适当的训练。 - 提供正确的工作方法和工具。 - 建立适当的激励机制促使工作得以完成。 …...
)
交换机基础(二)
一、VLAN 基础知识 虚拟局域网 (Virtual Local Area Network,VLAN) 是一种将局域网设 备从逻辑上划分成一个个网段,从而实现虚拟工作组的数据交换技术。 这一技术主要应用于3层交换机和路由器中,但主流应用还是在3层交换机中。 VLAN 是基于物理网络上构建…...

回归预测 | MATLAB实现基于BP-Adaboost的BP神经网络结合AdaBoost多输入单输出回归预测
回归预测 | MATLAB实现基于BP-Adaboost的BP神经网络结合AdaBoost多输入单输出回归预测 目录 回归预测 | MATLAB实现基于BP-Adaboost的BP神经网络结合AdaBoost多输入单输出回归预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现基于BP-Adaboost的BP…...
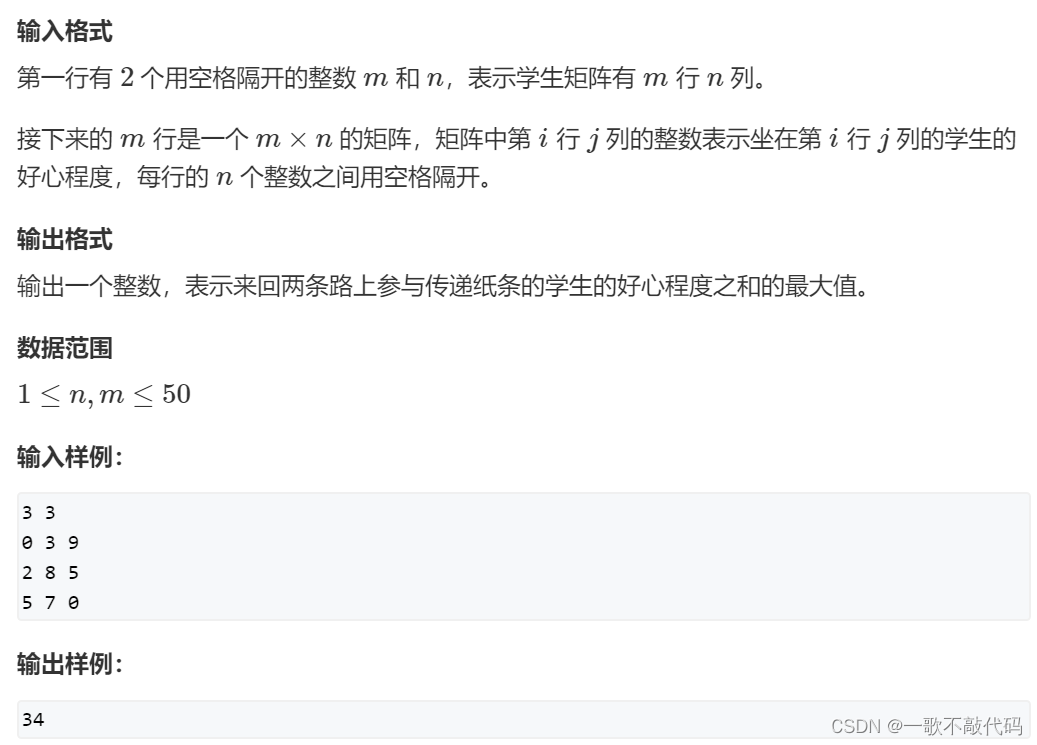
【蓝桥每日一题]-动态规划 (保姆级教程 篇11)#方格取数2.0 #传纸条
目录 题目:方格取数 思路: 题目:传纸条 思路: 题目:方格取数 (跑两次) 思路: 如果记录一种方案后再去跑另一个方案,影响因素太多了,所以两个方案要同时开…...

前端TypeScript学习day05-索引签名、映射与类型声明文件
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 索引签名类型 映射类型 索引查询(访问)类型 基本使用 同时查询多个索引的类型…...
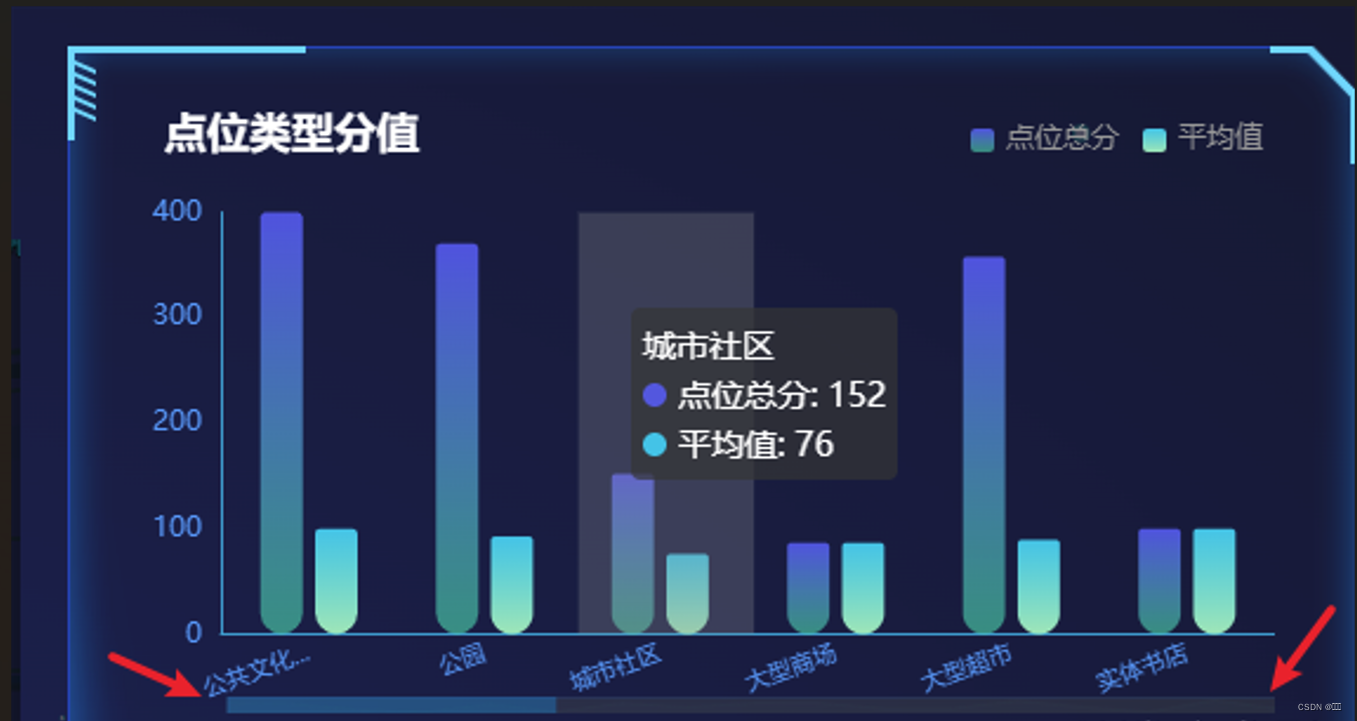
Echarts柱状图数据过多设置滚动条效果
未设置前: 设置后: dataZoom: [ { show: true, height:8, bottom:0, startValue: 0, //起始值 endValue: 5, //结束值 showDetail: fals…...

64 最长公共子序列
最长公共子序列 题解1 DP 给定两个字符串 text1 和 text2,返回这两个字符串的 最长公共子序列的长度。如果不存在 公共子序列,返回 0 。 一个字符串的子序列是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些…...

matlab常用函数
绘图函数 一、plot():二维图形绘制 1、plot(y): 对于只含一个输入参数的plot函数,如果输入参数y为向量,则以该参数为纵坐标,横坐标从1开始至与向量的长度相等;如果输入参数y是矩阵时,则按列绘…...

Python配置镜像源
Python3安装pika的准备 Windows下配置镜像源可以按照如下操作。 1.winR执行%APPDATA% %APPDATA%后,创建pip文件夹,并创建pip.ini配置文件 查看此目录下是否有pip目录,如果没有则需要创建,并在pip目录下以文本方式添加pip.ini文件…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
